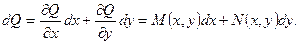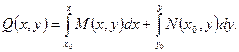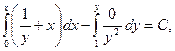Постановка задачи коши для дифференциального уравнения первого порядка (7 видео)

Постановка задачи коши для дифференциального уравнения первого порядка

Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах…
Часть II. Глава IV. Обыкновенные дифференциальные уравнения

Содержание

§ 1. Дифференциальные уравнения первого порядка
Дифференциальные уравнения первого порядка. Постановка задачи Коши.
Задача Коши — методы и примеры решения дифференциальных уравнений
Принцип и понятие
Алгоритм нахождения
Примеры задач
Операционный метод
Использование онлайн-калькулятора
📺 Видео

Видео:Задача Коши для дифференциальных уравненийСкачать

§ 1. Дифференциальные уравнения первого порядка

1. Основные понятия. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функцию и производные (или дифференциалы) этой функции. Если независимая переменная одна, то уравнение называется обыкновенным; если же независимых переменных две или больше, то уравнение называется дифференциальным уравнением в частных производных.

Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Например:

1) х²у’ + 5xy = у² – обыкновенное дифференциальное уравнение первого порядка;

2) – обыкновенное дифференциальное уравнение второго порядка;

3) y’³ + y»y»’ = х – обыкновенное дифференциальное уравнение третьего порядка;

4) F (х, у, у’, у») = 0 – общий вид обыкновенного дифференциального уравнения второго порядка;

5) – уравнение в частных производных первого порядка.

В этом параграфе рассматриваются обыкновенные дифференциальные уравнения первого порядка, т. е. уравнения вида F (х, у, у’) = 0 или (в разрешенном относительно у’ виде) y’ = f(х, у).

Решением дифференциального уравнения называется такая дифференцируемая функция у = φ (x), которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения.

Общим решением дифференциального уравнения первого порядка у’ = f(x, у) в области D называется функция у = φ(x, C), обладающая следующими свойствами: 1) она является решением данного уравнения при любых значениях произвольной постоянной С, принадлежащих некоторому множеству; 2) для любого начального условия у(х0) = у0 такого, что (x0; y0) ∈ 0, существует единственное значение С = С0, при котором решение у = φ(x, C0) удовлетворяет заданному начальному условию.

Всякое решение у = φ(x, C0), получающееся из общего решения у = φ (x, C) при конкретном значении С = С0, называется частным решением.

Задача, в которой требуется найти частное решение уравнения y’ = f(х, у) удовлетворяющее начальному условию у(х0) = y0, называется задачей Коши.

Построенный на плоскости хОу график всякого решения у = φ(х) дифференциального уравнения называется интегральной кривой этого уравнения. Таким образом, общему решению у = φ(х, С) на плоскости хОу соответствует семейство интегральных кривых, зависящее от одного параметра – произвольной постоянной С, а частному решению, удовлетворяющему начальному условию y(x0) = y0, – кривая этого семейства, проходящая через заданную точку М0(x0; у0).

Если функция f(х, у) непрерывна и имеет непрерывную производную в области D, то решение дифференциального уравнения у’= f (х, у) при начальном условии у(х0) = у0 существует и единственно, т. е. через точку (x0; y0) проходит единственная интегральная кривая данного уравнения (теорема Коши).

Особым решением называется такое решение, во всех точках которого условие единственности не выполняется, т. е. в любой окрестности каждой точки (х; у) особого решения существуют по крайней мере две интегральные кривые, проходящие через эту точку.

Особые решения не получаются из общего решения дифференциального управления ни при каких значениях произвольной постоянной С (в том числе и при С = ± ∞).

Особым решением является огибающая семейства интегральных кривых (если она существует), т. е. линия, которая в каждой своей точке касается по меньшей мере одной интегральной кривой.

Например, общее решение уравнения записывается в виде у = sin (х + С). Это семейство интегральных кривых имеет две огибающие: у = 1 и у = -1, которые и будут особыми решениями.

2. Дифференциальные уравнения с разделяющимися переменными. Дифференциальное уравнение вида

относится к типу уравнений с разделяющимися переменными. Если ни одна из функций f1(x), f2(y), φ1(x), φ2(y) не равна тождественно нулю, то в результате деления исходного уравнения на f2 (x) φ1 (y) оно приводится к виду

Почленное интегрирование последнего уравнения приводит к соотношению

которое и определяет (в неявной форме) решение исходного уравнения. (Решение дифференциального уравнения, выраженное в неявной форме, называют интегралом этого уравнения.)

507. Решить уравнение х(у²-4)dx + y dy = 0.

△ Разделив обе части уравнения на у² – 4 ≠ 0, имеем

x² + ln|у² – 4| = ln|C|, или у² – 4 = Сe -λ²

Это общее решение данного дифференциального уравнения.

Пусть теперь у² – 4 = 0, т. е. у = ± 2. Непосредственной подстановкой убеждаемся, что у = ±2 – решение исходного уравнения. Но оно не будет особым решением, так как его можно получить из общего решения при С = 0. ▲

508. Найти частный интеграл уравнения у’ cos х = у / ln у, удовлетворяющий начальному условию y(0) = l.

△ Полагая , перепишем данное уравнение в виде

Проинтегрируем обе части уравнения:

, или

Используя начальное условие у = 1 при х = 0, находим С = 0. Окончательно получаем

▲

509. Найти общий интеграл уравнения у’ = tg x tg y.

△ Полагая и разделяя переменные, приходим к уравнению ctg у dy = tg х dx. Интегрируя, имеем

, или ln|sin у| = -ln|cos x| + ln С.

Отсюда находим sin y = C/cos x, или sin y / cos x = С (общий интеграл). ▲

510. Найти частное решение дифференциального уравнения (l + x²)dy + y dx = 0 при начальном условии у(1) = 1.

△ Преобразуем данное уравнение к виду . Интегрируя, получим

, или ln |y| = – arctg x + С

Это и есть общий интеграл данного уравнения.

Теперь, используя начальное условие, найдем произвольную постоянную С; имеем ln 1 = — arctg 1 + С, т. е. С = π/4. Следовательно,

ln у = – arctg х + π/4,

откуда получаем искомое частное решение y = e π/4 – arctg x . ▲

Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах… Ч. II. Стр. 117-119.

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Дифференциальные уравнения первого порядка. Постановка задачи Коши.

Рассмотрим дифференциальное уравнение первого порядка.

Общий вид уравнения первого порядка

Если это уравнение разрешить относительно 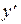, то есть

(12)

то уравнение называется уравнением первого порядка, разрешенным относительно производной.

Определение 4.Общим решением дифференциального уравнения (12) называется дифференцируемая функция

(13)

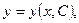
которая зависит от одной произвольной постоянной С и обращает это уравнение в тождество.

Определение 5. Частным решением уравнения (12) называется решение, получаемое из общего решения (13) при каком-либо определенном значении произвольной постоянной С.

Рассмотрим дифференциальное уравнение первого порядка в симметричной относительно x и y форме:

(14)

При некоторых условиях уравнение (3) эквивалентно, по крайней мере, одному из дифференциальных уравнений вида:

Дифференциальное уравнение определяет в каждой точке (x,y), где существует функция f(x,y), значение то есть угловой коэффициент касательной к интегральной кривой в этой точке. Таким образом, дифференциальное уравнение (12) определяет поле направлений.

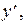
Задачи интегрирования дифференциального уравнения заключаются в том, чтобы найти интегральные кривые, направления касательных к которым в каждой точке совпадают с направлением поля. Для построения интегральных кривых используют метод изоклин.

Определение 6. Изоклиной называется геометрическое место точек, в которых касательные к искомым интегральным кривым сохраняют постоянное направление.

Семейство изоклин дифференциального уравнения (12) определяется уравнением

, (15)

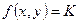
Постановка задачи Коши.

Задача о нахождении частного решения дифференциального уравнения, удовлетворяющего некоторым дополнительным условиям, часто встречается в приложениях. Если эти условия относятся к одному и тому же значению аргумента искомой функции, то их называют начальными. В том случае, когда начальные условия для дифференциального уравнения состоят в задании фиксированных значений функции и ее производных, их называют условиями Коши, а задачу – задачей Коши.

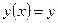
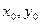
Задачей Коши для дифференциального уравнения (12) называют задачу нахождения решения уравнения удовлетворяющего начальному условию (где — заданные числа, называемые начальными значениями или данными).

Геометрически это означает, что ищется интегральная кривая, проходящая через заданную точку плоскости XOY.

Теорема. (о существовании и единственности решений задачи Коши.)

Пусть функция и ее производные определены и непрерывны на открытом множестве . Тогда в некоторой окрестности точки существует непрерывное решение задачи Коши:

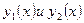
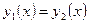
Замечание. Это решение единственно, т.е. если — два непрерывных решения задачи Коши, то для всех значений, при которых эти решения определены.

Как известно, общее решение уравнения (12) задается следующим равенством

(16)

Чтобы выделить частное решение уравнения (12), достаточно знать значение первообразной в какой – либо точке. Пусть, например, Тогда из соотношения (16) имеем или , т. е. решение единственно и равно

(17)

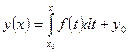
Уравнение (17) называется частным решением задачи Коши.

Пример 3. Решить задачу Коши.

Решение. Согласно формуле (17) частное решение имеет вид

Классы дифференциальных уравнений, интегрируемых в квадратурах.

Определение 7. Дифференциальное уравнение первого порядка называется интегрируемым в квадратурах (или просто интегрируемым), если его общее решение может быть получено с помощью конечного числа алгебраических операций и квадратур.

Рассмотрим уравнение (14).

Определение 8. Уравнение (14) называется точным уравнением или уравнением в полных дифференциалах, если существует дифференцируемая функция , для которой левая часть уравнения (14) является полным дифференциалом, т.е.

Пример 4. Для уравнения общий интеграл записывается в виде (это легко проверить непосредственным дифференцированием). Очевидно, что интегральные линии, определяемые общим интегралом, являются концентрическими окружностями с центром в начале координат.

Теорема. Пусть функции 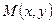и непрерывно дифференцируемы на открытом множестве D. Для того чтобы уравнение (14) было точным необходимо, чтобы выполнялось условие

(18)

Доказательство. Пусть уравнение (14) является точным. Тогда из определения точного уравнения и понятия полного дифференциала вытекает, что

(19)

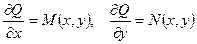
Дифференцируя первое равенство по y, а второе – по x, имеем

Так как смешанные производные непрерывны, то они равны и, значит, справедливо условие (18). Что и требовалось доказать.

Пусть D – односвязная область. Покажем, что в этом случае условие (18) является достаточным. Проинтегрируем первое из равенств (19) по x, считая y постоянным:

, (20)

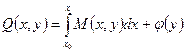
где — постоянная интегрирования, зависящая от y, а — абсцисса любой точки из области единственности D. Подберем функцию так, чтобы выполнялось второе из равенств (19). Для этого продифференцируем равенство (20) по y, считая x постоянным:

Откуда получим

Следовательно, т.е.

(21)

где — ордината произвольной точки из области единственности D, а произвольную постоянную считаем равной нулю. Из соотношений (20) и (21) получим

Итак, если в области D, не содержащей особых точек уравнения (12), выполнено условие (18), то общий интеграл уравнения выражается формулой

(22)

где C – произвольная постоянная.

Пример 5. Решить уравнение .

Решение. Обозначим и проверим выполнение условия (18): т.е. Это уравнение в полных дифференциалах и его общий интеграл имеет вид (22), где — любая точка из области . Положим, например, , тогда

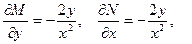
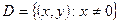
Интегрируя, находим Обозначив через получим общий интеграл исходного уравнения.

Интегрирующий множитель.

В том случае, когда условие (18) не выполняется, уравнение (14) не является уравнением в полных дифференциалах. Однако его можно проинтегрировать, если найти такую функцию , при умножении на которую всех членов уравнения оно становится точным:

(23)

Такая функция называется интегрирующим множителем уравнения (14). Общее решение уравнения (23) совпадает с общим решением уравнения (14).

Докажем, что для всякого уравнения (14), где M и N – непрерывно дифференцируемые функции, существует интегрирующий множитель. Пусть уравнение (14) не является точным. В силу теоремы существования и единственности решения, оно имеет общее решение в неявном виде. Дифференцируя это равенство по x, получим Так как из уравнения (14) следует , то . Обозначим через общую величину этих двух равных отношений; тогда

(24)

Поскольку 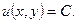есть общий интеграл уравнения (14), имеем Отсюда с учетом соотношения (24) получим уравнение вида (23), которое является точным. Следовательно, — интегрирующий множитель уравнения.

Пример 6. Решить уравнение .

Решение. Проверим выполнение условия (18):

, следовательно, это не уравнение в полных дифференциалах. Составим отношение

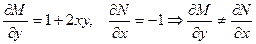
Найдем интегрирующий множитель

Тогда соответствующее точное уравнение будет иметь вид:

Область единственности этого уравнения есть 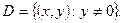Пусть . Находим общий интеграл

откуда, интегрируя, получим

Видео:Пример 65. Решить задачу Коши (диффуры)Скачать

Задача Коши — методы и примеры решения дифференциальных уравнений

Видео:Задача Коши ДУ I п. 1. Caushy`s ProblemСкачать

Принцип и понятие

Под задачей Коши для дифференциального уравнения понимают выражение вида: y’ = f (x, y) с начальным условием, соответствующим равенству: y (x0) = y0. По сути, это обозначает, что необходимо найти такое решение уравнения, которое проходит через заданную точку игрек и икс нулевое. Решением задачи называется функция, заданная на указанном интервале в окрестности точки икс нулевое, то есть: x Є (x0 — q, x0 + q).

Для проведения анализа функции должны выполняться следующие критерии:

Следует отметить, что решение Коши включает в себя и сам интервал икс нулевое плюс минус кью, фактически q-окрестность. Это обозначает, что одна и та же функция, задаваемая одной формулой, но рассматриваемая на разных интервалах, представляет два разных нахождения задачи Коши. Отсюда возникает вопрос, при каких же ответах существует решение Коши, а также когда оно будет единственным.

Существует теорема, гарантирующая единственность какого-то решения задачи. На самом деле возможность аналитического подхода Коши требует лишь главного условия, при котором функция f будет непрерывной в какой-то окрестности точки x0, y0. Но для доказательства единственности этого недостаточно. Для нормального случая необходимо следующее:

Функция f (x, y) непрерывна в некоторой окрестности точки (x0, y0).
Существует такая константа C, что для любых точек икс и игрек выполняется неравенство: |f (x, y) — f (x2, y2)| ⩽ C |y1 — y2|.

По игреку функция должна иметь обыкновенный рост, то есть не убыстряющийся (локальный подъём не превышать линейный). Если эти два условия выполняются, то решение Коши существует и оно будет единственным. Это значит, что тогда у точки икс нулевое найдётся такая окрестность, в которой существует решение и к тому же оно будет единственным.

А это обозначает, что любая другая функция в этой окрестности, удовлетворяющая уравнениям начальных условий, совпадает с той, существование которой утверждается. При этом на практике проверка условия на самом деле вещь не очень сложная, особенно если функция f (y) имеет в окрестности ограниченную производную.

Видео:Видеоурок "Дифференциальные уравнения. Задача Коши"Скачать

Алгоритм нахождения

Пусть имеется функция у’ = 2 * √ |y| и условие что y (0) = 0. Необходимо её исследовать. Тут можно заметить, что в этом случае функция зависит только от игрека и условию не удовлетворяет. В окрестностях точки с координатами (0, 0) она не удовлетворяет условию, так как любая окрестность захватывает ноль, а у корня квадратного по игреку будет бесконечная производная.

Это приводит не к единственности получения результатов. Так, у уравнения есть два решения: y1 тождественный нулю; y2 равняется x2. Согласно условию, игрек стоит по модулю, точнее, можно сказать, что для отрицательных значений икс будет меньше ноля, а положительных — больше.

Главный же вопрос заключается в продолжаемости анализа. Доказывается возможность простым построением решения с использованием специальных условий. В итоге должна быть найдена окрестность в точке x0. То есть берётся уравнение и точка с начальными координатами, затем выясняется, что в окрестности выполнены условия теоремы и строится решение.

Затем исследуется другая точка и изучается структура её окрестности. Например, обнаруживается, что условия существования единственности выполняются. Согласно теореме, тогда можно будет строить решение, где в качестве начальной точки будет взята любая координата. Другими словами, получается более широкое решение. Поэтому возникает вопрос, насколько можно приблизить точность ответа. Практические примеры показывают, что иногда можно двигаться до бесконечности, а в некоторых случаях сделать не более трёх шагов.

Если есть два уравнения y’ = f (x, y); y (x0) = y0 имеющие два решения: y1 (x), x Є I1 (эX), y2 (x), x єI2 (єX0). Тогда можно утверждать, что игрек два будет продолжением решения y1 (x) если в I2 входит I1, а y2 (x) равняется y1 (x) для любого икс из интервала I1. Следует учесть, что в этом определении в качестве областей функции всегда рассматривается интервал.

В изучении исследуются и матричные функциональные системы, состоящие из нескольких переменных A (z 1, z 2, …, zn). При этом z являются вещественными, а элементы матрицы могут быть как вещественными, так и комплексными. Исходя из этого даётся определение того, что функция, описываемая матрицей, непрерывна тогда, когда все элементы непрерывны в точке или на некотором множестве.

При определении используют численные и векторные функции от аргумента: y = (x), где y — это столбец от набора игреков, а икс со штрихом — от набора иксов. Таким образом, обобщённым решением будет такое действие, которое не будет иметь нетривиального продолжения, то есть вторые интервалы содержать первые.

Видео:Дифференциальные уравнения | уравнения первого порядка | задача Коши | конкретные примеры | 1Скачать

Примеры задач

На практических занятиях по высшей математике студентам предлагается для понимания курса выполнить ряд практических заданий. Существует типовой набор задач, научившись решать которые учащийся досконально разберётся в теме. Вот некоторые из них.

Первый пример. Имеется уравнение y’ = (2y / x lnx) + 1/x, для которого установлено начальное условие y (e) = 0. Необходимо найти решение, проходящее через точку e. Перед тем как приступить непосредственно к решению, необходимо отметить, что функция f (x, y) определённа всюду, за исключением прямых x = 0 и x = 1. Отсюда следует, что краевое решение не может быть вычислено на интервале от нуля до единицы.

В этом примере должен содержаться интервал, имеющий координату точки e по иксу. Он не может включать значения меньше единицы, так как необходимо, чтобы выполнялось заданное условием уравнение, которое в точке x = 1 теряет смысл, ведь в ней функция неопределённа. Установив это, можно переходить к анализу уравнения.

Заданное равенство является линейным — неоднородным уравнением первого порядка. Для решения нужно сначала рассмотреть левое соотношение: y’ = 2y / x * lnx. Добавив константу, уравнение можно переписать как y = c * e. Теперь необходимо взять интеграл исходя из первообразной формулы: ∫ 2 dx / (x *lnx).

После того как будет найдена постоянная, через общий интегральный метод с учётом условия определения функции, уравнение в окрестности точки e будет иметь решение вида: y = ln2x — lnx. Из полученного выражения можно сделать вывод, что функция будет определена для всех положительных иксов, но рассматривать её необходимо от единицы до плюс бесконечности. Это и будет максимальное непродолжаемое решение задачи: xЄ (1, + ∞).

Второй пример. Пусть имеется функция y’ = y / (1+x 2 ) с начальным условием: y = y (0). В задании нужно будет рассмотреть дифференциальную кривую уравнения, проходящего через точку y0. Нужно заметить, что функция f (x, y) в любой ограниченной области двумерной плоскости удовлетворяет условию регулярности для теоремы существования единственности. В задаче спрашивается, каким должен быть y0, если предел максимального решения при иксе, стремящемся к плюс бесконечности, равняется единице.

Учитывая, что в этой постановке заложено, чтобы решение было определённо до плюс бесконечности и то, что уравнение является однородно линейным, по общей формуле особое решение будет иметь вид: y = c * e arctgx . Игрек нулевое не может равняться нулю, ведь в ином случае решением уравнения будет тождественный ноль и заданное условие выполняться не будет. В итоге получится, что y = y0 * e arctgx . Это решение и является подходящей функцией для любого интервала.

Видео:Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 2Скачать

Операционный метод

Решение задачи Коши (примеров) целесообразно выполнять экономичным методом интегрирования линейных выражений, содержащих постоянные коэффициенты. Суть способа сводится к решению алгебраических равенств или неравенств. Алгоритм исследования заключается в следующих действиях:

Функции Y (p) и F (p) обозначают как изображения для y (x) и f (x).
Используя главные преобразования Лапласа, обрабатывая изображения, получают (pn (Yp) — p n -1 y 0 — …- yn -1) + a 1 (p n -1 y (p) — p n -2 y 0 — … — yn -2) + … + anY (p) = F (p) или, A (p)Y (p)+B (p) = F (p), причём A (p) и B (p) являются многочленами.
Найденное решение y (p) = (F (p) — B (p)) / A (p) и будет искомым y (x) для искомого y (p).

Например, пусть необходимо решить уравнение вида: x» + 4x = sin (2t), при x (0) = 1, x'(0) = -2. Классическим методом находить ответ довольно трудоёмко, поэтому имеет смысл для заданного уравнения использовать операционное исчисление. Для начала следует ввести замену Lx = x. Затем к обеим частям равенства применить преобразование Лапласа: Lx » + L 4 x = L * sin (2 t). Отсюда: Lx = x, Lx » = p 2 x — px (0) — x'(0). Функция Лапласа используется для преобразования вещественной переменной в выражение с комплексной переменной и наоборот. Это и позволяет использовать её при решениях дифференциальных уравнений и систем.

На следующем этапе нужно подставить исходные данные в равенство: Lx» = p 2 x — p + 2. Далее, следует выполнить преобразование и выразить неизвестную функцию. В итоге должно получиться выражение: X = (p 3 — 2 p 2 — 4 p — 6) / (p 2 + 4) 2 . Теперь можно найти оригинал изображений: x = L-1 = cos (2t) — sin (2t) + (sin (2t) — 2tcos (2t))/8.

Видео:Решить задачу КошиСкачать

Использование онлайн-калькулятора

Часто решение задач по рассматриваемой теме связано с большими трудозатратами. Это касается времени и повышенного внимания. На практике не всегда получается правильно применить алгоритм и избежать ошибок. Поэтому имеет смысл для сложных заданий использовать онлайн-калькулятор. Решения на задачу Коши с его помощью доступны любому заинтересованному, имеющему доступ к интернету и устройство, поддерживающее работу веб-обозревателя.

В интернете существует довольно большое количество различных математических онлайн-решителей. В своём большинстве они бесплатны и ориентированы на работу даже с людьми, совершенно не разбирающимися в тематике. Поэтому они привлекательны не только как инструмент, предоставляющий быстрый и правильный ответ на поставленную задачу, но и как обучающие программы.

Всё дело в том, что на страницах сервисов, предлагающих такого рода услуги, содержится вся необходимая теоретическая информация. Кроме этого, они предлагают к рассмотрению типовые примеры с подробным объяснением решения. Из онлайн-калькуляторов, предоставляющих бесплатный доступ к своим услугам в русском сегменте интернета, можно отметить следующие:

Math.semestr.
Allcalc.
Kontrolnaya-rabota.
Matematikam.
Primat.

Приведённые сервисы помогают без труда найти студентам решение дифференциального уравнения с заданными начальными условиями. Для этого в предлагаемую форму необходимо записать дифуравнение и через запятую начальные данные. Затем просто нажать интерактивную кнопку «Решить» и через некоторое время на экране дисплея отобразится ответ.

Для правильной записи уравнения существуют подсказки, так что разобраться, как работает сайт, сможет пользователь даже со слабой компьютерной подготовкой. Кроме этого, некоторые сервисы предлагают не просто ответ, а и пошаговое решение, к которому даётся комментарий. Решив несколько заданий, учащийся сможет разобраться в алгоритме и вычислять уравнения уже самостоятельно.

Следует отметить, что предложенные сервисы могут находить ответ для любой сложности математической задачи, например, вычисляя устойчивость математических моделей. Они также востребованы в инженерии и научных исследованиях, связанных с анализом функций. Для таких расчётов важны точность и время, что вполне могут обеспечить математические онлайн-сервисы.