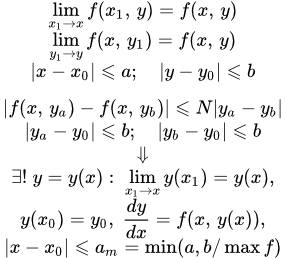М етод последовательных приближений (или метод Пикара) является аналитическим, т. е. позволяет получить приближённое решение задачи Коши, определяемой дифференциальным уравнением (1) с начальным условием (2), в виде формулы. Возник метод в связи с доказательством теоремысуществования и единственности решения задачи Коши (гл. 1).
Пусть в условиях данной теоремы требуется найти решение уравнения (1) с начальным условием (2). Проинтегрируем обе части уравнения (1) от х0 доx:

у(х) = у0 + 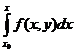
Очевидно, что решение интегрального уравнения (7) будет удовлетворять уравнению (1) и начальному условию (2). Действительно, при х =х0 получим
у(х0) = у0 + 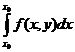
Применим к интегральному уравнению (7) метод последовательных приближений. Заменим в равенстве (7) неизвестную функцию у данным значением у0, получим первое приближение
у1(х) = у0 + 
Заметим, что интеграл в правой части содержит только одну переменную х, поэтому аналитическое выражение первого приближения у1(х) будет являться функцией, зависящей
от х.Заменим теперь в равенстве (7) неизвестную функцию у найденным значением у1(х), получим второе приближение
у2(х) = у0 +
и т. д. В общем случае итерационная формула имеет вид
уn(х) = у0 + 
Применив неоднократно формулу (8), получим последовательность функций
Можно доказать [1, 2, 3], что эта последовательность сходится и

т.е. предел последовательности является решением интегрального уравнения (7), а следовательно, и дифференциального уравнения (1) с начальным условием (2). Это означает, что k-й член последовательности (9) является приближением к точному решению уравнения (1)
с определённой степенью точности.
Погрешность k-го приближения можно оценить формулой
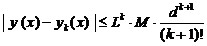
где L — постоянная Липшица; М — верхняя грань модуля функции f, т.е. 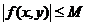
величина d для определения окрестности 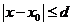

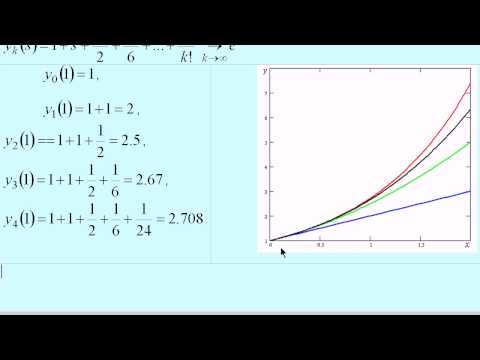
Пример 1. Найти три последовательных приближения решения дифференциального уравнения у’ = x + y 2 ,удовлетворяющего начальному условию у(0) = 1.
Решение.В качестве начального приближения возьмём
первое приближение у1(х) = у0 + 

второе приближение у2(х) = у0 + 
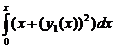
третье приближение у3(х) = у0 + 

Вычисления интегралов и построение графиков полученных функций у1(х), у2(х), у3(х) проведём в системе MathCAD. Результаты решения представлены на рис. 14.
Оценим погрешность третьего приближения.
Для определения области G, заданной неравенствами (6), примема = 1, b = 2. Получим
G: – 1 



В прямоугольнике G функция
определена и непрерывна, причём: 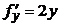




По формуле (10) получим

 |
Рис. 14
Заметим, что в программе MathCAD для вычисления интегралов с переменным верхним пределом интегрирования, необходимо выполнить следующие действия:
1) записать интеграл и выделить его в рамку;
2) выбрать команду Evaluate (Вычислить) из меню опции Simbolic (Символика) главного меню.
Существует и другой способ вычисления несобственных интегралов в программе MathCAD, по которому следует:
1) записать интеграл и выделить его в рамку;
2) выбрать команду Simplify (Упростить) из меню опции Simbolic (Символика) главного меню.
Пример 2. Найти пять последовательных приближений решения дифференциального уравнения
удовлетворяющего начальному условию у(0) = 0.
Сравнить полученные приближения с точным решением.
Решение.В качестве начального приближения возьмём
Решение данного уравнения, проведённое в системе MathCAD, показано на рис. 15.
 |
Рис. 15
МетодЭйлера
М етод Эйлера относится одновременно к численным и к графическим методам решения дифференциальных уравнений.
Суть метода заключается в том, что искомую интегральную кривую y = y(x) заменяют ломаной M0M1M2 . звенья которой являются касательными к интегральным кривым (рис. 16).
Рис. 16
Пусть требуется решить задачу Коши, т.е. найти решение дифференциального уравнения (1) с начальным условием (2) в виде функции y = y(x). Выбрав шаг h, построим, начиная
с точки х0, систему равноотстоящих точек:
Вместо искомой интегральной кривойy = y(x) на отрезке [х0, х1]рассмотрим отрезок касательной L1 к ней в точке М0 (х0, y0). Уравнение касательной L1, в силу (1), имеет вид
При х = х1 из уравнения касательной L1 получим
откуда видим, что приращение функции на первом шаге имеет вид

Аналогично, проводя касательную L2 к некоторой интегральной кривой семейства в точке М1(х1, y1), получим

Таким образом, значения искомой функции y(x) могут быть определены по формулам:
yi+1 =yi + 

где i= 0,1,2, . , которые называются вычислительными формулами метода Эйлера.
При этом искомую интегральную кривую y = y(x), проходящую через точку М0 (х0, y0), приближённо заменяем так называемой ломаной ЭйлераM0M1M2 . звенья которой MiMi+1 прямолинейны между прямыми x = xi, x = xi+1 и имеют подъём

Метод Эйлера является простейшим численным методом, удобным в применении, однако он имеет ряд существенных недостатков. Основной из них — малая точность. Она равна порядку h 2 , причём с каждым шагом погрешность возрастает, т.е. происходит систематическое накопление ошибок. Поэтому на практике часто используют способ двойного счёта — с шагом hи с шагом h/2. Совпадение десятичных знаков в полученных двумя способами результатах даёт естественные основания считать их верными.
Пример.
1. Найти методом Эйлера численное решение дифференциального уравнения
у’ = x 3 + y,удовлетворяющее начальному условию у (0) = 1, на отрезке [0, 1] с шагом h = 0,1.
2. Найти точное решение уравнения у’ = x 3 + y и сравнить его с приближённым на отрезке [0, 1].
1. Для данного уравнения вычислительные формулы (11) имеют вид:
yi+1 =yi + 

Учитывая, что погрешность метода имеет порядок h 2 = 0,01, достаточно в промежуточных результатах брать три цифры после запятой, а во всех yiсохранять только две цифры.
Результаты вычислений оформим в виде таблицы.
| i | х i | yi |  yi = hf( х i , yi) = 0,1( х i 3 + yi) yi = hf( х i , yi) = 0,1( х i 3 + yi) |
| 0 | 0 | 1 | 0,1 |
| 1 | 0,1 | 1,1 | 0,110 |
| 2 | 0,2 | 1,21 | 0,122 |
| 3 | 0,3 | 1,33 | 0,136 |
| 4 | 0,4 | 1,47 | 1,634 |
| 5 | 0,5 | 1,62 | 0,175 |
| 6 | 0,6 | 1,79 | 0,201 |
| 7 | 0,7 | 1,99 | 0,233 |
| 8 | 0,8 | 2,22 | 0,273 |
| 9 | 0,9 | 2,49 | 0,322 |
| 10 | 1 | 2,82 | — |
2. Данное уравнение у’ = x 3 + y является линейным дифференциальным уравнением первого порядка. Решим его методом Бернулли.
Полагая y = uv, имеем

Сгруппируем члены, содержащие uв первой степени, получим

Полагаем 



Для нахождения uимеем уравнение
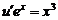
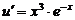
Разделим переменные, получим 

Интегрируем по частям три раза:

Таким образом, общее решение данного уравнения
y = uv = 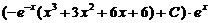
или y = 
Используя начальное условие у (0) = 1, получим 1 = ‑ 6 + С, откуда С = 7. Следовательно, искомое частное (точное) решение имеет вид
у = 
Вычислим значения полученного точного решения на отрезке [0, 1] с шагом h = 0,1. Результаты округлим до 0,01 и запишем в таблицу.
| i | х i | Приближённые значения yi | Точные значения y (х i ) |
| 0 | 0 | 1 | 1 |
| 1 | 0,1 | 1,1 | 1,11 |
| 2 | 0,2 | 1,21 | 1,22 |
| 3 | 0,3 | 1,33 | 1,35 |
| 4 | 0,4 | 1,47 | 1,5 |
| 5 | 0,5 | 1,62 | 1,67 |
| 6 | 0,6 | 1,79 | 1,86 |
| 7 | 0,7 | 1,99 | 2,08 |
| 8 | 0,8 | 2,22 | 2,35 |
| 9 | 0,9 | 2,49 | 2,66 |
| 10 | 1 | 2,82 | 3,03 |
Сравнение приближённого (численного) решения данного дифференциального уравнения с точным на промежутке [0, 1] проведём с помощью системы MathCAD.
Результаты сравнения, а также численное решение данного уравнения, проведённое методом Эйлера в системе MathCAD, представлены на рис. 17.
 |
Рис. 17
МодификацииметодаЭйлера
Существуют различные уточнения метода Эйлера, повышающие его точность. Цель модификаций — более точно определить направление перехода из точки (х i, yi) в точку (х i +1, yi +1). Так, метод Эйлера-Коши предлагает вычислять значения искомой функции y(x) по формулам:
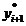
yi+1 = yi + h 
Геометрически это означает, что мы определяем направление интегральной кривой в исходной точке (х i, yi) и во вспомогательной точке (х i +1, 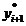
Другой модификацией метода Эйлера является усовершенствованный метод ломаных, при котором сначала вычисляют промежуточные значения:

и находят значение направления поля интегральных кривых в средней точке ( 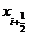


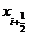

yi+1 = yi + h 
Метод Эйлера и его модификации являются простейшими представителями конечно-разностных методов (шаговых методов) для приближённого решения задачи Коши.
Поскольку описанные методы предполагают повторяющиеся вычисления на каждом шаге, то они легко программируются и могут быть реализованы на компьютере.
На рис. 18 и 19 показаны решения дифференциального уравнения у’ = x 3 + y,удовлетворяющего начальному условию у(0) = 1, полученные модифицированными методами Эйлера (методом Эйлера-Коши и усовершенствованным методом ломаных) с помощью системы MathCAD.
 |
Рис. 18
 |
Рис. 19
Метод Рунге-Кутта
Рассмотренный выше метод Эйлера относится к семейству методов Рунге-Кутта и является их простейшим частным случаем (методом первого порядка точности). Наиболее известным из методов Рунге-Кутта является классический четырёхэтапный метод четвёртого порядка точности. Его расчётные формулы для решения задачи Коши, определённой уравнениями (1) и (2), имеют вид:
yi+1 =yi + 


k2 (i) = h f (х i + 

k3 (i) = h f (х i + 

Погрешность метода на каждом шаге является величиной порядка h 5 .
Геометрический смысл использования метода Рунге-Кутта с вычислительными формулами (12) состоит в следующем (рис. 20).
 |
Рис. 20
Из начальной точки М0(х0, y0) сдвигаются в направлении, определяемом углом 

х = х0 + 
Затем из точки М0(х0, y0)сдвигаются в направлении, определяемом углом 




Далее из точки М0(х0, y0) сдвигаются в направлении, определяемом углом 


(х0 + h, y0 + k3 (0) ). Этим задаётся ещё одно направление, определяемое углом 

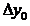

На этом окончательном направлении и выбирается очередная точка М1с координатами (х1, y1) = (х0+ h, y0 + 
Теперь, уже исходя из точки М1, все построения с помощью усреднений направлений повторяют сначала. Идут в новом усреднённом направлении до вертикальной прямой х = х2, получают точку М2(х2, y2) и т.д.
Эффективная оценка метода Рунге-Кутта затруднительна [2, 4]. Поэтому для определения правильности выбора шага h на практике обычно на каждом этапе из двух шагов применяют двойной пересчёт, а именно: исходя из текущего верного значения y(х i) вычисляют величину y(х i+ 2h) двумя способами: один раз с шагом h, другой раз — с двойным шагом 2h .
Если расхождение полученных значений не превышает допустимой погрешности, то шаг hдля данного этапа выбран правильно и полученное с его помощью значение можно принять за y (х i+ 2h). В противном случае шаг уменьшают в два раза.
На практике при вычислениях по формулам (15) обычно пользуются схемой, приведённой в таблице.
| i | x | Y | k = hf (х, y ) |  у у |
| 0 | х 0 х0 +  х0 + х0 +  х0 + h х0 + h | y 0 y0 +  y0 + y0 +  y0 + k3 (0) y0 + k3 (0) | k1 (0) k2 (0) k3 (0) k4 (0) | k1 (0) 2k2 (0) 2k3 (0) k4 (0) |
| — | — | — | — |  |
| 1 | х1 | y1 | . . . | . . . |
Пример. Найти методом Рунге-Кутта решение дифференциального уравнения у’ = x 3 + y,удовлетворяющего начальному условию у(0) = 1, на отрезке [0, 1] с шагом h = 0,1.
Решение.Учитывая, что погрешность метода имеет порядок h 5 = 0,00001, в промежуточных результатах следует брать пять цифр после запятой, а во всех yiсохранять только четыре цифры. Результаты вычислений оформим в виде таблицы.
| i | х | y | k = 0,1(х 3 + y ) |  y y |
| 0 | 0 0,05 0,05 0,1 | 1 1,05 1,0525 1,1053 | 0,1 1,10501 1,10526 1,11063 | 0,1 0,21003 0,21053 0,11063 |
| 0,1052 | ||||
| 1 | 0,1 0,15 0,15 0,2 | 1,1052 1,1604 1,1634 1,2219 | 0,11062 0,11637 0,11668 0,11136 | 0,11062 0,23278 0,21121 0,11136 |
| 0,10556 | ||||
| 2 | 0,2 0,25 0,25 0,3 | 1,2218 1,2717 1,2752 1,3399 | 0,12188 0,12874 0,12908 0,13669 | 0,12188 0,25747 0,25816 0,13669 |
| 0,12903 | ||||
| 3 | 0,3 0,35 0,35 0,4 | 1,3520 1,4081 1,4124 1,4853 | 0,13668 0,1451 0,14552 0,15493 | 0,13668 0,2902 0,29105 0,15493 |
| 0,14548 | ||||
| 4 | 0,4 0,45 0,45 0,5 | 1,4988 1,5628 1,568 1,6512 | 0,15493 0,16539 0,16591 0,17762 | 0,15493 0,33078 0,33182 0,17762 |
| 0,16586 | ||||
| 5 | 0,5 0,55 0,55 0,6 | 1,6661 1,74 1,7465 1,8425 | 0,17762 0,19064 0,19132 0,20585 | 0,17762 0,38128 0,38258 0,20585 |
| 0,19122 | ||||
| 6 | 0,6 0,65 0,65 0,7 | 1,8588 1,9618 1,9699 2,0826 | 0,20584 0,22199 0,2228 0,24082 | 0,20584 0,44399 0,4456 0,24082 |
| 0,22271 | ||||
| 7 | 0,7 0,75 0,75 0,8 | 2,0833 2,1855 2,1955 2,3268 | 0,24081 0,26074 0,26173 0,28388 | 0,24081 0,52148 0,52347 0,28388 |
| 0,26161 | ||||
| 8 | 0,8 0,85 0,85 0,9 | 2,3468 2,4898 2,5021 2,6585 | 0,28589 0,3104 0,31162 0,33875 | 0,28589 0,62079 0,62324 0,33875 |
| 0,31145 | ||||
| 9 | 0,9 0,95 0,95 1 | 2,6582 2,8545 2,8695 3,0566 | 0,34129 0,37119 0,37269 0,40566 | 0,34129 0,74238 0,74537 0,40566 |
| 0,37245 | ||||
| 10 | 1 | 3,0280 |
Соответствующее решение данного дифференциального уравнения, полученное методом Рунге-Кутта в системе MathCAD, представлено на рис. 21.
 |
Рис. 21
Лабораторная работа
«Численные методы решения задачи Коши
для обыкновенных дифференциальных уравнений»
Задание 1.
1. Для заданного дифференциального уравнения первого порядка у’ = f(x , y) c начальным условием у (a) = c найти приближённое решение в виде многочлена пятой степени.
2. Найти численное решение данного дифференциального уравнения на отрезке [a, b] с шагом интегрирования h, округляя результат до 0,001.
3. Найти точное решение заданного дифференциального уравнения у’ = f (x, y) и сравнить его с приближённым на отрезке [a, b]. Построить графики полученных решений.
Исходные данные для 15-ти вариантов содержатся в таблице.
| Вариант | f ( x , y ) | a | b | с | h |
| 1 |  | 0 | 1 | 0 | 0,1 |
| 2 |  | 0 | 1 | 1 | 0,1 |
| 3 |  | 0 | 2 | 0 | 0,1 |
| 4 |  | p | 2p | 0 | p/10 |
| 5 |  | 1 | 2 | 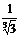 | 0,1 |
| 6 |  | 1 | 3 | 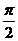 | 0,2 |
| 7 | 4 +  | 1 | 2 | 2 | 0,1 |
| 8 |  | 1 | 2 | 0 | 0,2 |
| 9 |  | 0 | 2 | 0 | 0,1 |
| 10 |  | 0 | 2 | 1 | 0,2 |
| 11 |  | 1 | 2 | 0 | 0,2 |
| 12 | –  | 0 | 1 | p/4 | 0,1 |
| 13 | –  |  |  | е | 0,1 |
| 14 |  | 0 | 1 | 1 | 0,1 |
| 15 |  | 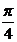 | 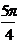 | 0 | 0,3 |
Указания к выполнению задания 1
1. Для того, чтобы получить приближённое решение заданного дифференциального уравнения в виде многочлена пятой степени, используйте формулу (3) при k = 0, 1, . 5.
2. При выборе метода для вычисления точного решения учитывайте то, что дифференциальные уравнения вариантов 1- 4 являются линейными дифференциальными уравнениями, уравнение 5-го варианта — уравнение Бернулли, уравнения 6-8-х вариантов — однородные дифференциальные уравнения, а уравнения 9-15-х го вариантов — дифференциальные уравнения с разделяющимися переменными.
3. Для сравнения точного и приближённого решений заданного дифференциального уравнения сначала составьте таблицы их значений на отрезке [a , b], затем постройте на этом же отрезке графики полученных решений.
Задание 2. Решить задачу Коши для обыкновенного дифференциального уравнения первого порядка у’ = f(x , y) на отрезке [a , b]при заданном начальном условии у(a) = c и шаге интегрирования h:
1) методом Эйлера с шагом 2h и с шагомh;
2) модифицированным методом Эйлера (методом Эйлера — Коши или усовершенствованным методом ломаных);
3) методом Рунге-Кутта с шагом 2h и с шагомh.
Результаты округлить до 0,0001. Сравнить полученные разными методами решения. Построить графики полученных решений.
- Метод последовательных приближений решения дифференциального уравнения
- Теорема Коши существования и единственности решения дифференциального уравнения первого порядка
- Формулировка теоремы
- Условие Липшица
- Доказательство существования решения
- 1) Доказательство существования предела yn при n стремящемся к бесконечности
- 2) Доказательство того, что Y является решением (4)
- Доказательство единственности решения
- 📹 Видео
Видео:Метод Пикара последовательных приближений для решения дифференциальных уравненийСкачать

Метод последовательных приближений решения дифференциального уравнения
Пусть требуется найти решение дифференциального уравнения
Будем предполагать, что в некотором прямоугольнике для уравнения (1) выполнены условия а) и б) теоремы существования и единственности решения задачи (1)-(2).
Решение задачи (1)-(2) может быть найдено методом последовательных приближений , который состоит в следующем.
Строим последовательность функций, определяемых рекуррентными соотношениями
В качестве нулевого приближения можно взять любую функцию, непрерывную в окрестности точки , в частности — начальное значение Коши (2). Можно доказать, что при сделанных предположениях относительно уравнения (1) последовательные приближения сходятся к точному решению уравнения (1), удовлетворяющему условию (2), в некотором интервале , где
Оценка погрешности, получаемой при замене точного решения n-м приближением , даётся неравенством
где . Применяя метод последовательных приближений, следует остановиться на таком , для которого не превосходит допустимой погрешности.
Пример 1. Методом последовательных приближений найти решение уравнения , удовлетворяющее начальному условию .
Решение. Очевидно, что для данного уравнения на всей плоскости выполнены условия теоремы существования и единственности решения задачи Коши. Строим последовательность функций, определяемых соотношениями (3), приняв за нулевое приближение :
Ясно, что при . Непосредственной проверкой убеждаемся, что функция решает поставленную задачу Коши.
Пример 2. Методом последовательных приближений найти приближенное решение уравнения , удовлетворяющее начальному условию в прямоугольнике
Решение. Имеем , т. е. . За берем меньшее из чисел , т. е. . Последовательные приближения согласно (4) будут сходится в интервале . Составляем их
Абсолютная погрешность третьего приближения не превосходит величины
Замечание. Функция должна удовлетворять всем условиям теоремы существования и единственности решения задачи Коши.
Следующий пример показывает, что одной непрерывности функции недостаточно для сходимости последовательных приближений.
Пусть функция определена следующим образом:
На множестве , функция непрерывна и ограничена постоянной . Для начальной точки последовательные приближения при имеют вид:
Поэтому последовательность для каждого не имеет, предела, т. е. последовательные приближения не сходятся. Заметим также, что ни одна из сходящихся подпоследовательностей и не сходится к решению, поскольку
Если же последовательные приближения сходятся, то полученное решение может оказаться неединственным , как показывает следующий пример: .
Возьмем начальное условие ; тогда
Беря в качестве нулевого приближения функцию , будем иметь
так что все последовательные приближения равны нулю и поэтому они сходятся к функции, тождественно равной нулю. С другой стороны, функция представляет собой также решение этой задачи, существующее на полупрямой .
Видео:Решаем диффуры методом последовательных приближенийСкачать

Теорема Коши существования и единственности решения дифференциального уравнения первого порядка
Впервые существование решения дифференциального уравнения было доказано Коши. Приводимое ниже доказательство основано на методе последовательных приближений, который принадлежит Пикару. Этот метод имеет самостоятельное значение, поскольку позволяет получить приближенное решение дифференциального уравнения.
Видео:5. Метод последовательных приближенийСкачать
Формулировка теоремы
Пусть дано дифференциальное уравнение первого порядка:
(1)
с начальным условием
(1.1) .
Пусть – непрерывная функция двух переменных в замкнутой области :
и, следовательно, ограничена некоторым положительным значением :
(2) .
И пусть функция удовлетворяет условию Липшица:
(3) ,
.
Тогда существует единственное решение уравнения (1):
,
удовлетворяющее начальному условию , определенное и непрерывное для значений в интервале:
,
где есть наименьшее из двух чисел и .
Условие Липшица
Рассмотрим условие Липшица. Оно имеет вид:
(3) ,
где – положительное число;
, и – любые значения из области :
, , .
Смысл условия Липшица легко понять, если записать его в виде:
(3.1) .
При некотором фиксированном значении переменной , функция является функцией от переменной : . Пусть мы имеем график этой функции. Возьмем две точки, принадлежащие , на этом графике и проведем через них прямую. Тогда угол между прямой и осью ограничен некоторым значением , которое меньше . При таком ограничении график не имеет вертикальных касательных и скачков. А в тех точках, где существует частная производная , она ограничена:
.
Если в области функция имеет непрерывную частную производную , то в этой области выполняется условие Липшица (3).
Для доказательства заметим, что поскольку частная производная непрерывна в замкнутой области, то она ограничена:
.
По теореме Лагранжа о конечных приращениях, имеем:
,
где частные производные вычисляются в некоторой точке , в которой переменная принадлежат интервалу между и :
.
Тогда:
.
Видео:Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 2Скачать

Доказательство существования решения
Приведем исходное уравнение (1) с начальным условием (1.1) к интегральному уравнению. Левая и правая части (1) являются функциями от . Заменим на :
.
Интегрируем это уравнение по от до :
;
Подставим начальное условие . В результате получим интегральное уравнение:
(4) .
Покажем, что интегральное уравнение (4) эквивалентно дифференциальному уравнению (1) с начальным условием (1.1). Для этого нужно показать, что из (1) и (1.1) следует (4) и из (4) следует (1) и (1.1). То, что из (1) и (1.1) следует (4) мы уже показали. Осталось показать, что из (4) следует (1) и (1.1). Для этого подставим в (4) . Получим начальное условие (1.1). Продифференцировав обе части уравнения (4) по , получаем уравнение (1).
Далее мы пытаемся найти решение уравнения (4) с помощью последовательных приближений. Для этого определяем ряд функций от переменной по формулам:
(5.1) ;
(5.2) ;
(5.3) ;
.
(5.n) .
Мы предполагаем, что при , стремится к решению уравнения (4):
(6) ,
где – решение уравнения (4). Если мы докажем это, то мы докажем существование решения.
Доказательство существования решения будем проводить в два этапа:
1> вначале докажем, что предел (6) существует;
2) затем докажем, что удовлетворяет уравнению (4):
.
1) Доказательство существования предела yn при n стремящемся к бесконечности
Сведем последовательные приближения (5.1) – (5.n) к сумме ряда. Для этого пишем:
.
Таким образом нам нужно доказать, что ряд
(7)
сходится при .
Сначала покажем, что при , последовательные приближения принадлежат интервалу .
Действительно, при имеем:
.
Поскольку есть наименьшее из двух чисел и , то и
.
Далее, поскольку принадлежит интервалу , то . Тогда, аналогично предыдущему,
.
Отсюда
.
Далее, по индукции, поскольку принадлежат интервалу , то и
.
Отсюда
.
Итак, мы доказали, что последовательные приближения принадлежат интервалу
.
Теперь мы можем оценить члены ряда (7), применяя условие Липшица.
Для первого члена имеем:
;
(8.1) .
Для второго члена применяем условие Липшица и оценку (8.1):
;
(8.2) .
Для третьего члена применяем, аналогично, условие Липшица и оценку (8.2):
;
(8.3) .
Далее применим метод индукции. Пусть
(8.n) .
Тогда
;
(8.n+1) .
Итак, поскольку (8.n) справедливо для и из (8.n) следует (8.n+1), то (8.n) выполняется для любых .
Запишем ряд (7) в виде:
(7.1) ,
где .
Применим (8.n) и заменим наибольшим допустимым значением :
.
Тогда каждый член ряда (7.1) ограничен по модулю членом ряда
(9) .
Исследуем ряд (9) на сходимость. Применим признак Даламбера:
.
Итак, ряд (9) сходится. Поскольку все члены ряда (7.1), начиная со второго, по абсолютной величине меньше членов сходящегося ряда (9), то, в силу критерия Вейерштрасса, ряд (7.1) сходится равномерно для всех , удовлетворяющих условию . Поскольку интеграл есть непрерывная функция от верхнего предела, то каждый член ряда (7.1) есть непрерывная функция от . Поэтому предел
(10)
существует и является непрерывной функцией от .
2) Доказательство того, что Y является решением (4)
Рассмотрим уравнение (5.n):
(5.n) .
Докажем, что при , это уравнение стремится к уравнению
(11) .
В силу (10) левая часть уравнения (5.n) стремится к .
Теперь покажем, что
.
Перепишем правую часть (5.n):
.
Далее заметим, что поскольку все принадлежат закрытому интервалу , то и принадлежит этому интервалу, . Поэтому мы можем применить условие Липшица.
Оценим абсолютную величину последнего члена:
.
Поскольку, при , стремится к равномерно, то для любого положительного числа можно указать такое натуральное число , что для всех ,
.
Тогда
.
Поскольку произвольно, то
Поэтому
.
То есть при уравнение
(5.n)
принимает вид
(11) .
Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Доказательство единственности решения
Предположим, что уравнение
(4)
имеет два решения и , различающиеся в некоторой точке , принадлежащей интервалу .
Рассмотрим функцию
.
Будем считать, что . В противном случае поменяем местами и .
Поскольку и непрерывны, то и непрерывная функция. Поэтому она отлична от нуля в некотором интервале, содержащем точку :
при .
Поскольку , то . То есть точка не принадлежит этому интервалу.
Если , то преобразуем (4) следующим образом:
,
где
.
Если переобозначить постоянные
,
то получим задачу (4), для которой
;
при ,
где – некоторое число, не превосходящее .
Если , то поступаем аналогично:
,
Переобозначим постоянные:
.
Получаем задачу (4), для которой
;
при ,
где – некоторое число, не меньшее .
Итак, мы имеем:
;
при ( или при ).
Далее возьмем произвольное положительное число ( или ) и рассмотрим закрытый интервал ( или ). Поскольку функция непрерывна, то она достигает наибольшего значения в одной из точек этого интервала:
( или ).
Сделаем оценку, применяя уравнение (4) и условие Липшица:
;
.
Поскольку , то разделим на :
.
Возникает противоречие, поскольку при это неравенство не выполняется.
Следовательно, не может иметь отличных от нуля значений. Поэтому . Что и требовалось доказать.
Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Автор: Олег Одинцов . Опубликовано: 04-06-2016 Изменено: 20-06-2016
📹 Видео
Метод итераций (последовательных приближений)Скачать

Асташова И. В. - Дифференциальные уравнения I - Семинар 7Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Решение физических задач с помощью дифференциальных уравненийСкачать

Острые диффуры, или как научиться решать методом последовательных приближенийСкачать

Дифференциальные уравнения. 11 класс.Скачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Частное решение дифференциального уравнения. 11 класс.Скачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать