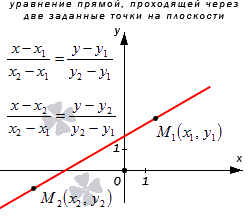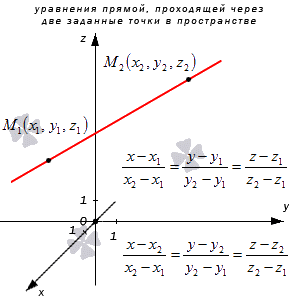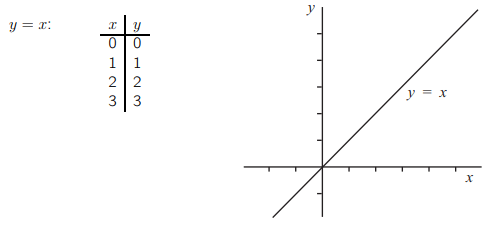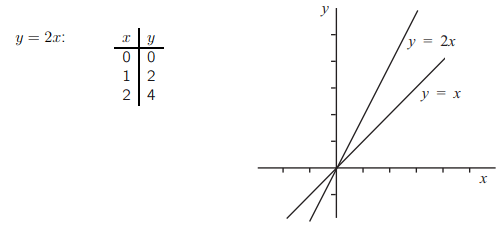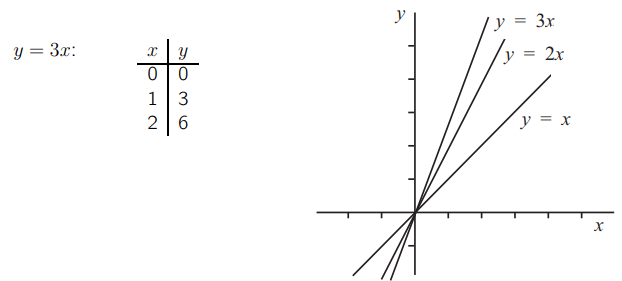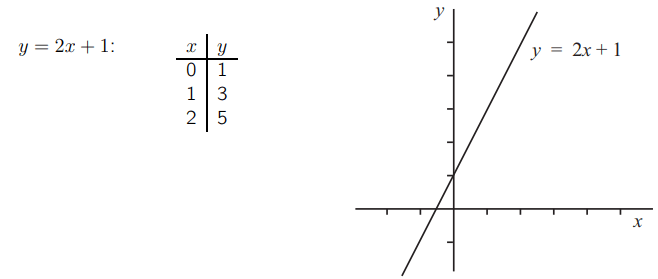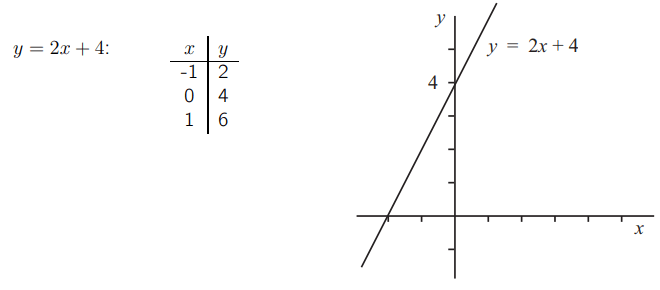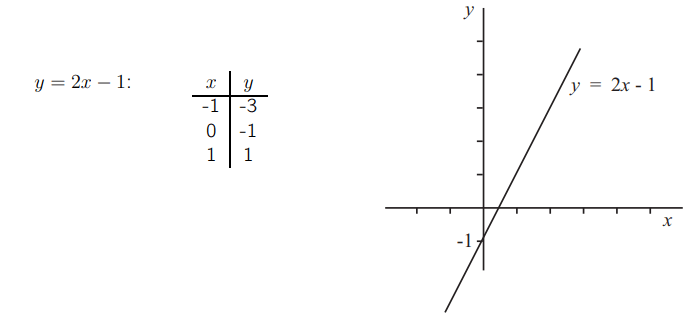Данная статья раскрывает получение уравнения прямой, проходящей через две заданные точки в прямоугольной системе координат, расположенной на плоскости. Выведем уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат. Наглядно покажем и решим несколько примеров, касающихся пройденного материала.
- Уравнение прямой, проходящей через две заданные точки на плоскости
- Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве
- Уравнение прямой проходящей через две точки
- Общее уравнение прямой на плоскости
- Приведение общего уравнения прямой на плоскости к каноническому виду
- Приведение общего уравнения прямой на плоскости к параметрическому виду
- Уравнение прямой, которая проходит через две заданные точки: примеры, решения
- Уравнение прямой, проходящей через начало координат с заданным коэффициентом
- Пересечение прямой y
- Уравнение прямой прямой с заданным коэффициентом, проходящее через заданную точку на оси у
- 📺 Видео
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнение прямой, проходящей через две заданные точки на плоскости
Перед получением уравнения прямой, проходящей через две заданные точки необходимо обратить внимание на некоторые факты. Существует аксиома, которая говорит о том, что через две несовпадающие точки на плоскости возможно провести прямую и только одну. Иначе говоря, две заданные точки плоскости определяются прямой линией, проходящей через эти точки.
Если плоскость задана прямоугольной системой координат Оху, то любая изображенная в нем прямая будет соответствовать уравнению прямой на плоскости. Также имеется связь с направляющим вектором прямой. Этих данных достаточно для того, чтобы произвести составление уравнения прямой, проходящей через две заданные точки.
Рассмотрим на примере решения подобной задачи. Необходимо составить уравнение прямой a , проходящей через две несовпадающие точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , находящиеся в декартовой системе координат.
В каноническом уравнении прямой на плоскости, имеющего вид x — x 1 a x = y — y 1 a y , задается прямоугольная система координат О х у с прямой, которая пересекается с ней в точке с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) .
Необходимо составить каноническое уравнение прямой a , которая пройдет через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) .
Прямая а имеет направляющий вектор M 1 M 2 → с координатами ( x 2 — x 1 , y 2 — y 1 ) , так как пересекает точки М 1 и М 2 . Мы получили необходимые данные для того, чтобы преобразовать каноническое уравнение с координатами направляющего вектора M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 ) и координатами лежащих на них точках M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 .
Рассмотрим рисунок, приведенный ниже.
Следуя по вычислениям, запишем параметрические уравнения прямой на плоскости, которое проходит через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ .
Рассмотрим подробней на решении нескольких примеров.
Записать уравнение прямой, проходящей через 2 заданные точки с координатами M 1 — 5 , 2 3 , M 2 1 , — 1 6 .
Каноническим уравнением для прямой, пересекающейся в двух точках с координатами x 1 , y 1 и x 2 , y 2 принимает вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . По условию задачи имеем, что x 1 = — 5 , y 1 = 2 3 , x 2 = 1 , y 2 = — 1 6 . Необходимо подставить числовые значения в уравнение x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . Отсюда получим, что каноническое уравнение примет вид x — ( — 5 ) 1 — ( — 5 ) = y — 2 3 — 1 6 — 2 3 ⇔ x + 5 6 = y — 2 3 — 5 6 .
Ответ: x + 5 6 = y — 2 3 — 5 6 .
При необходимости решения задачи с другим видом уравнения, то для начала можно перейти к каноническому, так как из него проще прийти к любому другому.
Составить общее уравнение прямой, проходящей через точки с координатами M 1 ( 1 , 1 ) и M 2 ( 4 , 2 ) в системе координат О х у .
Для начала необходимо записать каноническое уравнение заданной прямой, которая проходит через заданные две точки. Получим уравнение вида x — 1 4 — 1 = y — 1 2 — 1 ⇔ x — 1 3 = y — 1 1 .
Приведем каноническое уравнение к искомому виду, тогда получим:
x — 1 3 = y — 1 1 ⇔ 1 · x — 1 = 3 · y — 1 ⇔ x — 3 y + 2 = 0
Ответ: x — 3 y + 2 = 0 .
Примеры таких заданий были рассмотрены в школьных учебниках на уроках алгебры. Школьные задачи отличались тем, что известным было уравнение прямой с угловым коэффициентом, имеющее вид y = k x + b . Если необходимо найти значение углового коэффициента k и числа b , при которых уравнение y = k x + b определяет линию в системе О х у , которая проходит через точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , где x 1 ≠ x 2 . Когда x 1 = x 2 , тогда угловой коэффициент принимает значение бесконечности, а прямая М 1 М 2 определена общим неполным уравнением вида x — x 1 = 0 .
Потому как точки М 1 и М 2 находятся на прямой, тогда их координаты удовлетворяют уравнению y 1 = k x 1 + b и y 2 = k x 2 + b . Следует решить систему уравнений y 1 = k x 1 + b y 2 = k x 2 + b относительно k и b .
Для этого найдем k = y 2 — y 1 x 2 — x 1 b = y 1 — y 2 — y 1 x 2 — x 1 · x 1 или k = y 2 — y 1 x 2 — x 1 b = y 2 — y 2 — y 1 x 2 — x 1 · x 2 .
С такими значениями k и b уравнение прямой, проходящее через заданные две точки, принимает следующий вид y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 1 или y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 2 .
Запомнить сразу такое огромное количество формул не получится. Для этого необходимо учащать количество повторений в решениях задач.
Записать уравнение прямой с угловым коэффициентом, проходящей через точки с координатами M 2 ( 2 , 1 ) и y = k x + b .
Для решения задачи применяем формулу с угловым коэффициентом, имеющую вид y = k x + b . Коэффициенты k и b должны принимать такое значение, чтобы данное уравнение соответствовало прямой, проходящей через две точки с координатами M 1 ( — 7 , — 5 ) и M 2 ( 2 , 1 ) .
Точки М 1 и М 2 располагаются на прямой, тогда их координаты должны обращать уравнение y = k x + b верное равенство. Отсюда получаем, что — 5 = k · ( — 7 ) + b и 1 = k · 2 + b . Объединим уравнение в систему — 5 = k · — 7 + b 1 = k · 2 + b и решим.
При подстановке получаем, что
— 5 = k · — 7 + b 1 = k · 2 + b ⇔ b = — 5 + 7 k 2 k + b = 1 ⇔ b = — 5 + 7 k 2 k — 5 + 7 k = 1 ⇔ ⇔ b = — 5 + 7 k k = 2 3 ⇔ b = — 5 + 7 · 2 3 k = 2 3 ⇔ b = — 1 3 k = 2 3
Теперь значения k = 2 3 и b = — 1 3 подвергаются подстановке в уравнение y = k x + b . Получаем, что искомым уравнением, проходящим через заданные точки, будет уравнение, имеющее вид y = 2 3 x — 1 3 .
Такой способ решения предопределяет траты большого количества времени. Существует способ, при котором задание решается буквально в два действия.
Запишем каноническое уравнение прямой, проходящей через M 2 ( 2 , 1 ) и M 1 ( — 7 , — 5 ) , имеющее вид x — ( — 7 ) 2 — ( — 7 ) = y — ( — 5 ) 1 — ( — 5 ) ⇔ x + 7 9 = y + 5 6 .
Теперь переходим к уравнению в угловым коэффициентом. Получаем, что: x + 7 9 = y + 5 6 ⇔ 6 · ( x + 7 ) = 9 · ( y + 5 ) ⇔ y = 2 3 x — 1 3 .
Ответ: y = 2 3 x — 1 3 .
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве
Если в трехмерном пространстве имеется прямоугольная система координат О х у z с двумя заданными несовпадающими точками с координатами M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , проходящая через них прямая M 1 M 2 , необходимо получить уравнение этой прямой.
Имеем, что канонические уравнения вида x — x 1 a x = y — y 1 a y = z — z 1 a z и параметрические вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ способны задать линию в системе координат О х у z , проходящую через точки, имеющие координаты ( x 1 , y 1 , z 1 ) с направляющим вектором a → = ( a x , a y , a z ) .
Прямая M 1 M 2 имеет направляющий вектор вида M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 , z 2 — z 1 ) , где прямая проходит через точку M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , отсюда каноническое уравнение может быть вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 = z — z 2 z 2 — z 1 , в свою очередь параметрические x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ z = z 1 + ( z 2 — z 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ z = z 2 + ( z 2 — z 1 ) · λ .
Рассмотрим рисунок, на котором изображены 2 заданные точки в пространстве и уравнение прямой.
Написать уравнение прямой, определенной в прямоугольной системе координат О х у z трехмерного пространства, проходящей через заданные две точки с координатами M 1 ( 2 , — 3 , 0 ) и M 2 ( 1 , — 3 , — 5 ) .
Необходимо найти каноническое уравнение. Так как речь идет о трехмерном пространстве, значит при прохождении прямой через заданные точки, искомое каноническое уравнение примет вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 .
По условию имеем, что x 1 = 2 , y 1 = — 3 , z 1 = 0 , x 2 = 1 , y 2 = — 3 , z 2 = — 5 . Отсюда следует, что необходимые уравнения запишутся таким образом:
x — 2 1 — 2 = y — ( — 3 ) — 3 — ( — 3 ) = z — 0 — 5 — 0 ⇔ x — 2 — 1 = y + 3 0 = z — 5
Ответ: x — 2 — 1 = y + 3 0 = z — 5 .
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Уравнение прямой проходящей через две точки
Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.
Прямая — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.
Уравнения прямой, проходящей через две точки могут быть следующих видов:
- каноническое уравнение,
- параметрическое уравнение,
- общее уравнение прямой,
- уравнение прямой с угловым коэффициентом,
- уравнение прямой в полярных координатах и другие.
Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.
Видео:Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Общее уравнение прямой на плоскости
В данной статье мы рассмотрим общее уравнение прямой на плоскости. Приведем примеры построения общего уравнения прямой, если известны две точки этой прямой или если известна одна точка и нормальный вектор этой прямой. Представим методы преобразования уравнения в общем виде в канонический и параметрический виды.
Пусть задана произвольная декартова прямоугольная система координат Oxy. Рассмотрим уравнение первой степени или линейное уравнение:
где A, B, C − некоторые постоянные, причем хотя бы один из элементов A и B отлично от нуля.
Мы покажем, что линейное уравнение на плоскости определяет прямую. Докажем следующую теорему.
Теорема 1. В произвольной декартовой прямоугольной системе координат на плоскости каждая прямая линия может быть задана линейным уравнением. Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат на плоскости определяет прямую линию.
Доказательство. Достаточно доказать, что прямая L определяется линейным уравнением при какой нибудь одной декартовой прямоугольной системе координат, поскольку тогда она будет определяться линейным уравнением и при любом выборе декартовой прямоугольной системы координат.
Пусть на плоскости задана прямая L. Выберем систему координат так, чтобы ось Ox совпадал с прямой L, а ось Oy был перпендикулярной к ней. Тогда уравнение прямой L примет следующий вид:
Все точки на прямой L будут удовлетворять линейному уравнению (2), а все точки вне этой прямой, не будут удовлетворять уравнению (2). Первая часть теоремы доказана.
Пусть задана декартова прямоугольная система координат и пусть задана линейное уравнение (1), где хотя бы один из элементов A и B отличен от нуля. Найдем геометрическое место точек, координаты которых удовлетворяют уравнению (1). Так как хотя бы один из коэффициентов A и B отличен от нуля, то уравнение (1) имеет хотя бы одно решение M(x0,y0). (Например, при A≠0, точка M0(−C/A, 0) принадлежит данному геометрическому месту точек). Подставляя эти координаты в (1) получим тождество
| Ax0+By0+C=0. | (3) |
Вычтем из (1) тождество (3):
| A(x−x0)+B(y−y0)=0. | (4) |
Очевидно, что уравнение (4) эквивалентно уравнению (1). Поэтому достаточно доказать, что (4) определяет некоторую прямую .
Поскольку мы рассматриваем декартову прямоугольную систему координат, то из равенства (4) следует, что вектор с компонентами <x−x0, y−y0> ортогонален вектору n с координатами <A,B>.
Рассмотрим некоторую прямую L, проходящую через точку M0(x0, y0) и перпендикулярной вектору n (Рис.1). Пусть точка M(x,y) принадлежит прямой L. Тогда вектор 


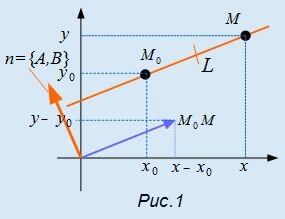 |
Вектор n=<A,B> называется нормальным вектором прямой L.
Замечание 1. Если два общих уравнения прямой
| A1x+B1y+C1=0 | (5) |
| A2x+B2y+C2=0 | (6) |
определяют одну и ту же прямую, то найдется такое число λ, что выпонены равенства
| A2=A1λ, B2=B1λ, C2=C1λ. | (7) |
| (A1λ−A2)x0+(B1λ−B2)x0+(C1λ−C2)=0. | (8) |
Так как выполнены первые два равенства из выражений (7), то C1λ−C2=0. Т.е. C2=C1λ. Замечание доказано.
Заметим, что уравнение (4) определяет уравнение прямой, проходящей через точку M0(x0, y0) и имеющий нормальный вектор n=<A,B>. Поэтому, если известен нормальный вектор прямой и точка, принадлежащая этой прямой, то можно построить общее уравнение прямой с помощью уравнения (4).
Пример 1. Прямая проходит через точку M=(4,−1) и имеет нормальный вектор n=. Построить общее уравнение прямой.
Решение. Имеем: x0=4, y0=−1, A=3, B=5. Для построения общего уравнения прямой, подставим эти значения в уравнение (4):
Упростив получим общее уравнение прямой:
Пример 2. Прямая проходит через точки M1=(−5, 2) и M2=(−2, 3). Построить общее уравнение прямой.
Решение. Вычислим вектор 
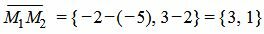 |
Вектор 

Для построения общего уравнения прямой воспользуемся формулой (4). Подставим в (4) координаты точки M1 (можем взять также координаты точки M2) и нормального вектора n:
Упростим полученное уравнение:
Подставляя координаты точек M1 и M2 в (9) можем убедится, что прямая заданная уравнением (9) проходит через эти точки.
Видео:Видеоурок "Уравнение прямой, проходящей через две точки"Скачать

Приведение общего уравнения прямой на плоскости к каноническому виду
Нам нужно привести уравнение (1) к каноническому виду. Для этого найдем некоторую точку M0(x0,y0) на этой прямой. Тогда имеем:
| Ax0+By0+C=0 | (10) |
| A(x−x0)+B(y−y0)=0 | (11) |
Вторую слагаемую уравнения (11) переместим на право и разделим обе части уравнения на −AB:
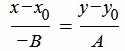 | (12) |
Мы получили каноническое уравнение прямой. Вектор q=<−B, A> является направляющим вектором прямой (12).
Обратное преобразование смотрите здесь.
Пример 3. Прямая на плоскости представлена следующим общим уравнением:
Привести данное уравнение прямой к каноническому виду.
Решение: Найдем некоторую точку на прямой (13). Для этого подставим в (13) y=1 и найдем x. Получим x=2. Запишем уравнение прямой пользуясь формулой (11):
Переместим на право вторую слагаемую и разделим обе части уравнения на 2·5:
 |
 |
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Приведение общего уравнения прямой на плоскости к параметрическому виду
В предыдущем параграфе мы привели общее уравнение прямой (1) к каноническому виду (12). Из канонического уравнения легко получить параметрическое уравнение прямой. для этого левый и правый части уравнения (12) обозначим через параметр t. Тогда получим:
 |
Выразив x и y через параметр t, получим параметрическое уравнение прямой:
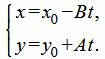 |
Обратное преобразование смотрите здесь.
Пример 4. Прямая на плоскости представлена следующим общим уравнением:
Привести данное уравнение прямой к параметрическому виду.
Решение: Найдем некоторую точку на прямой (13). Для этого подставим в (14) x=3 и найдем y. Получим y=11. Запишем уравнение прямой пользуясь формулой (11):
Переместим на право вторую слагаемую и разделим обе части уравнения на 5·2:
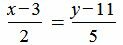 |
Обозначим обе части уравнения через параметр t:
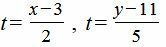 |
Выразим x и y через параметр t:
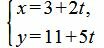 |
Ответ. Параметрическое уравнение прямой имеет следующий вид:
Видео:Составляем уравнение прямой по точкамСкачать

Уравнение прямой, которая проходит через две заданные точки: примеры, решения
Время чтения: 26 минут
В этой статье мы рассмотрим концепцию уравнения прямой прямой. Мы попытаемся понять общее уравнение прямой, формулу прямой, способ нахождения уравнения прямой и откроем для себя другие интересные аспекты этого. Попробуйте свои силы в решении нескольких интересных примеров и вопросов для лучшего понимания концепции.
Уравнение прямой — может быть записано в различных формах. Прямая линия -это двумерная геометрическая фигура, которая простирается на обоих своих концах до бесконечности.
Для того чтобы освоить описанные приемы, необходимо много практиковаться, чтобы они стали привычными.
После прочтения информации по этой теме вы должны уметь:
- находить уравнение прямой прямой, учитывая ее наклон и пересечение с осью y;
- находить уравнение прямой, учитывая ее наклон и одну точку, лежащую на ней;
- найти уравнение прямой, учитывая две точки, лежащие на ней;
- дать уравнение прямой в любой из форм y = mx + c или ax + by + c = 0
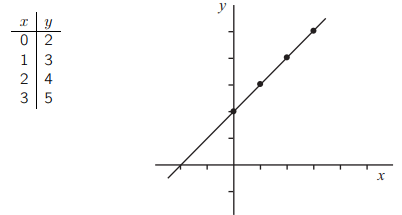
Уравнения прямых могут принимать различные формы в зависимости от фактов, которые мы знаем о прямых. Итак, для начала предположим, что у нас есть прямая линия содержащая точки из следующего списка.
На прямой есть еще много точек, но уже достаточно, чтобы увидеть закономерность. Если мы возьмем любое значение x и прибавим 2, мы получим соответствующее значение y: 0 + 2 = 2, 1 + 2 = 3, 2 + 2 = 4, и так далее. Между координатами x и y любой точки на прямой существует фиксированная зависимость, и уравнение y = x + 2 всегда верно для точек на прямой. Мы можем обозначить прямую, используя это уравнение.
Видео:Составить уравнение прямой, проходящей через две данные точки. Метод координат. Геометрия 9 классСкачать

Уравнение прямой, проходящей через начало координат с заданным коэффициентом
Предположим, что у нас есть прямая с уравнением y = x. Тогда для каждой точки на прямой координата y должна быть равна координате x. Таким образом, прямая будет содержать точки из следующего списка.
Мы можем найти коэффициент прямой, используя формулу для нахождения коэффициента:
Далее следует подставить первые два набора значений из таблицы. Получаем:
Таким образом, коэффициент этой прямой равен 1.
А как насчет уравнения y = 2x? Оно также представляет собой прямую линию, и для всех точек на y в два раза больше соответствующего значения x. Таким образом, линия будет содержать точки из следующем списке.
Если мы вычислим коэффициент прямой y = 2x, используя первые два набора значений в таблице, то получим:
Таким образом, коэффициент этой прямой равен 2.
Теперь возьмем уравнение y = 3x. Оно также представляет собой прямую линию, и для всех точек на прямой. Каждая точка y в три раза больше соответствующего значения x. Таким образом, линия будет содержать точки из следующего списка.
Если мы вычислим коэффициент прямой y = 3x, используя первые два набора значений в таблице, мы получим:
Следовательно, коэффициент этой прямой равен 3.
Мы можем начать видеть здесь закономерность. Все эти прямые имеют уравнения, где y равно некоторому числу, умноженному на x. И в каждом случае линия проходит через начало координат, а коэффициент прямой равен m.
Таким образом, если бы у нас была прямая с уравнением y = 13x, то мы бы указали, что коэффициент прямой будет равен 13. Аналогично, если бы у нас была прямая с уравнением y = -2x, то коэффициент будет равен -2. Таким образом, в общем случае уравнение y = mx представляет собой прямую линию, проходящую через начало координат с коэффициентом m.
Уравнение прямой с коэффициентом m, проходящей через начало координат, имеет вид:
Видео:Видеоурок "Общие уравнения прямой"Скачать

Пересечение прямой y
Рассмотрим прямую линию с уравнением y = 2x + 1. Это уравнение имеет несколько иную форму в отличие от тех, которые мы видели ранее. Чтобы нарисовать график прямой, мы должны вычислить некоторые значения.
Обратите внимание, что при x = 0 значение y равно 1. Значит, эта прямая пересекает ось y в точке y = 1.
А как насчет прямой y = 2x + 4? Мы снова можем вычислить некоторые значения.
Эта линия пересекает ось y в точке y = 4.
А как насчет прямой y = 2x — 1? Мы снова можем вычислить некоторые значения.
Эта линия пересекает ось y в точке y = — 1.
Общее уравнение прямой — y = mx + c, где m — коэффициент, а y = c — значение на оси у, при через которое проходим прямая.
Это число c является пересечением с осью y.
Уравнение прямой с коэффициентом m и точкой пересечения c на оси y имеет вид:
Иногда нам задают уравнение прямой в другой форме. Предположим, у нас есть уравнение 3y — 2x = 6. Как показать, что оно представляет собой прямую линию, и найти ее коэффициент и значение точки пересечения с осью y?
Мы можем использовать алгебраическую перестановку, чтобы получить уравнение в виде y = mx + c:
Теперь уравнение находится в стандартной форме, и мы видим, что коэффициент равен [frac], а значение точки пересечения с осью y равно 2.
Мы также можем работать в обратном направлении. Предположим, мы знаем, что прямая имеет коэффициент [frac] и имеет вертикальное пересечение в точке y = 1. Каким будет ее уравнение?
Чтобы найти уравнение, достаточно подставить нужные значения в общую формулу y = mx + c.
Здесь m равно [frac], а c — 1, поэтому уравнение равно y =[frac]x + 1. Если мы хотим убрать дробь, мы можем также привести уравнение к виду 5y = x + 5, или 5y — x — 5 = 0.
Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Уравнение прямой прямой с заданным коэффициентом, проходящее через заданную точку на оси у
Предположим, что мы хотим найти уравнение прямой с коэффициентом [frac], которое проходит через точку (1, 2). Здесь, хотя мы знаем коэффициент, мы не знаем значение точки пересечения с осью у, оно равно c.
Начнем с общего уравнения прямой y = mx + c.
Мы знаем, что коэффициент равен [frac], именно поэтому мы можем сразу подставить это значение на место m. Это дает: [y=frac x+c]
Теперь мы используем тот факт, что прямая проходит через (1, 2). Это означает, что когда x = 1, y должно быть равна 2. Подставляя эти значения, находим:
Таким образом, уравнение прямой имеет вид:
Мы можем вывести общую формулу для задач такого типа, используя тот же метод. Мы возьмем общую прямую с коэффициентом m, проходящую через фиксированную точку [mathrmleft(x_, y_right)].
Начнем с общего уравнения прямой y = mx + c. Теперь мы используем тот факт, что прямая проходит через точку [mathrmleft(x_, y_right)]. Это означает, что при x = [x_], y должно быть [y_]. Подставляя эти значения, находим:
Таким образом, уравнение прямой имеет вид y = mx + [y_-mathrm x_].
Мы можем записать его в альтернативной форме
Тогда это прямая с уклоном m, проходящая через точку [left(x_, y_right)]. Таким образом, эта общая форма полезна, если вы знаете коэффициент и одну точку на прямой.
Уравнение прямой с коэффициентом m, проходящей через точку [left(x_, y_right)], имеет вид:.
Например, мы знаем, что прямая имеет коэффициент -2 и проходит через точку (-3, 2).
Мы можем воспользоваться формулой [y-y_=mleft(x-x_right)] и сразу подставить значения:
Упражнение 1
Найдите уравнение описанных ниже прямых (приведите уравнение в виде y = mx + c):
(1) коэффициент 3, проходящей через (1, 4);
(2) коэффициент -2, проходящей через (2, 0);
(3) коэффициент [frac], проходящий через (5, -1);
(4) коэффициент 0, проходящий через (-1, 2);
(5) коэффициент -1, проходящий через (1, -1).
📺 Видео
1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Видеоурок "Канонические уравнения прямой"Скачать

№972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2)Скачать

Лекция 23. Виды уравнений прямой на плоскости.Скачать

Уравнение прямой на плоскостиСкачать

3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

12. Уравнения прямой в пространстве Решение задачСкачать

§51 Уравнение прямой в пространстве, проходящей через две точкиСкачать

4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать