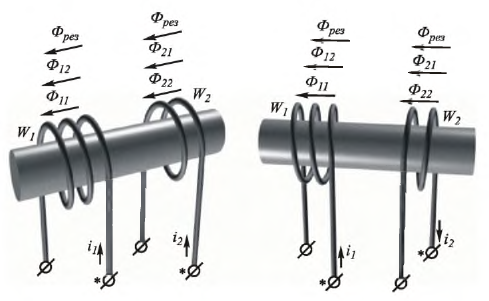
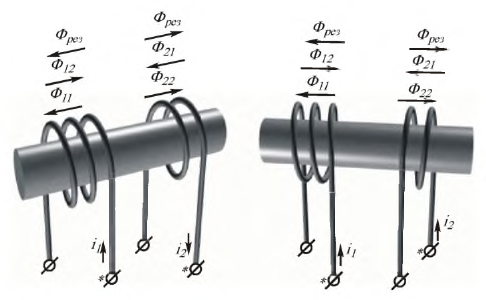
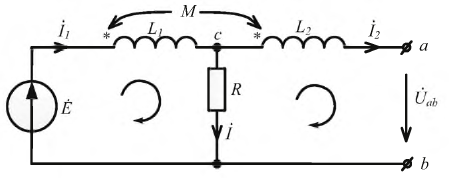
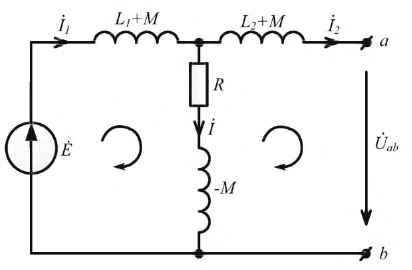
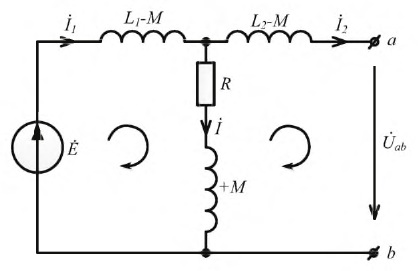
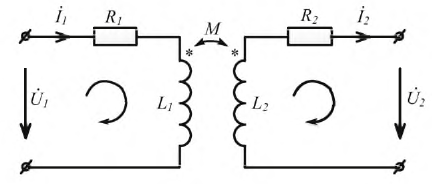
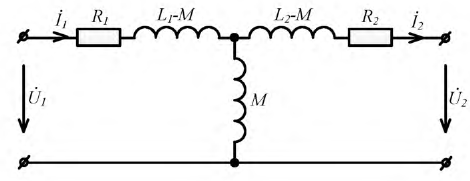
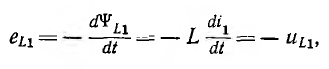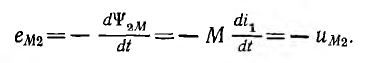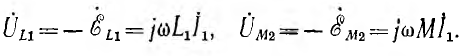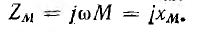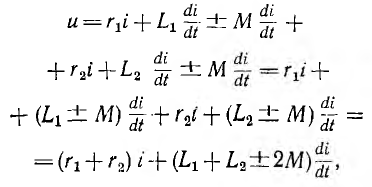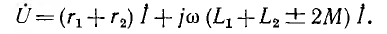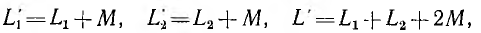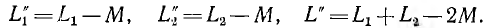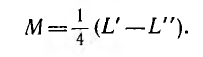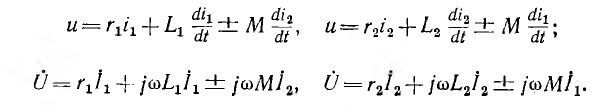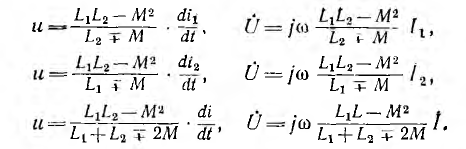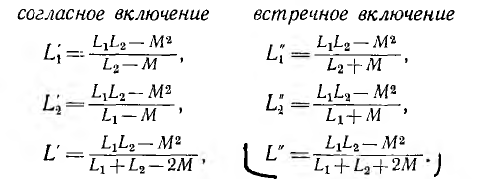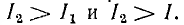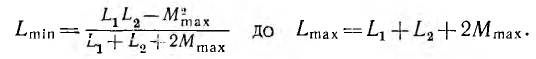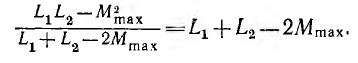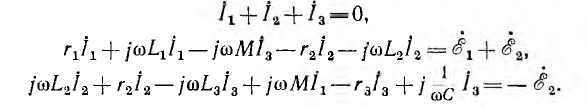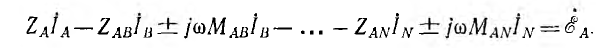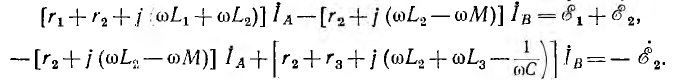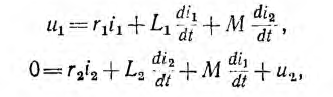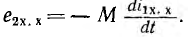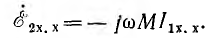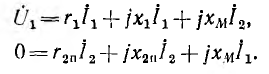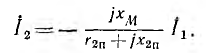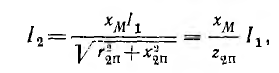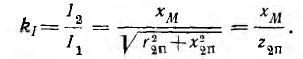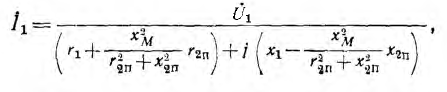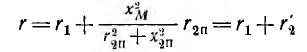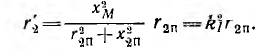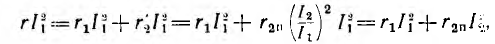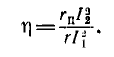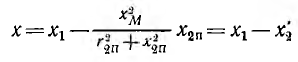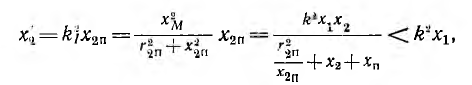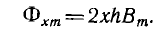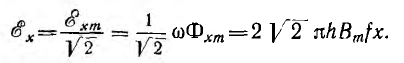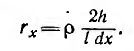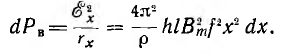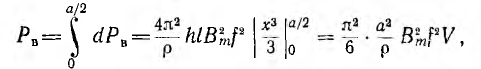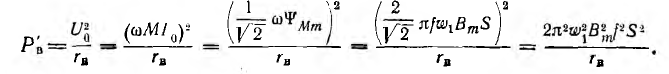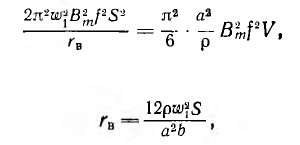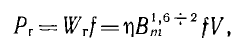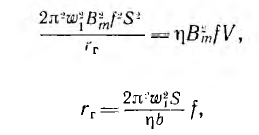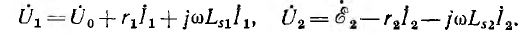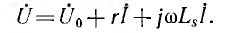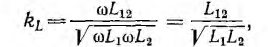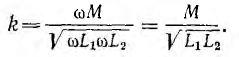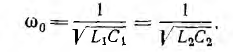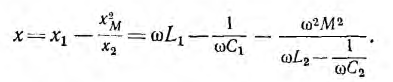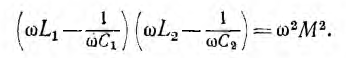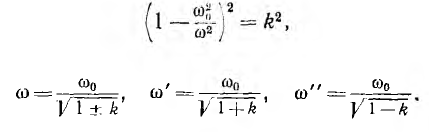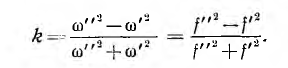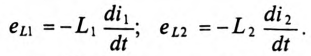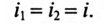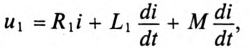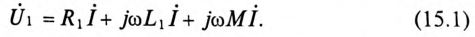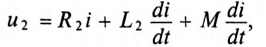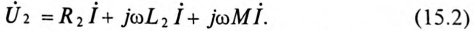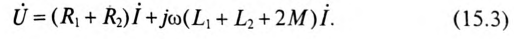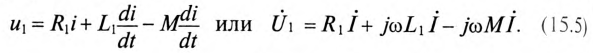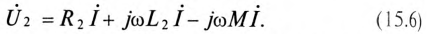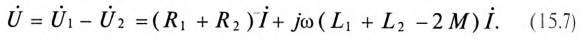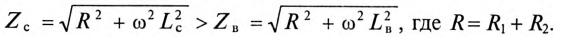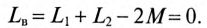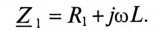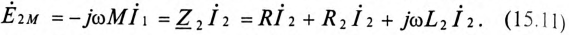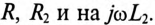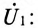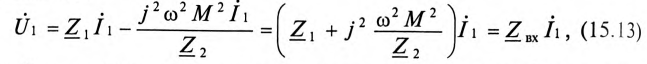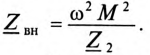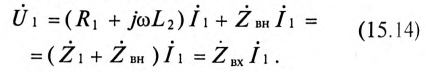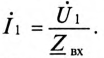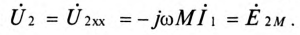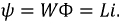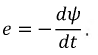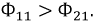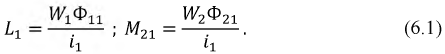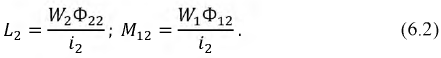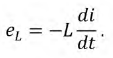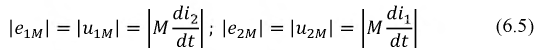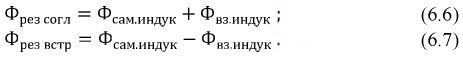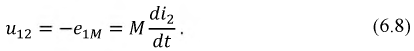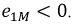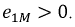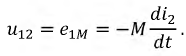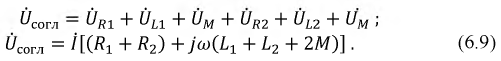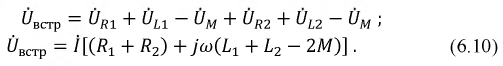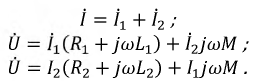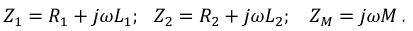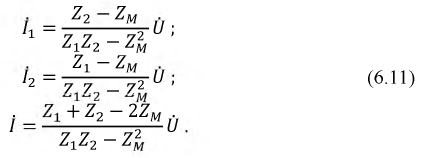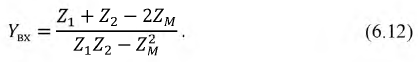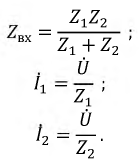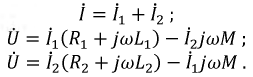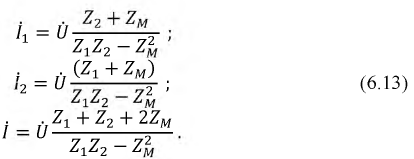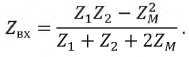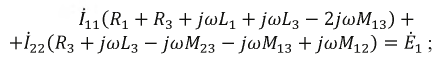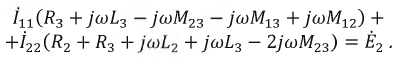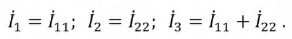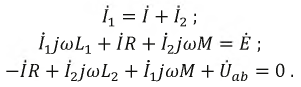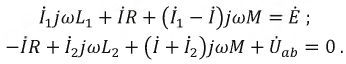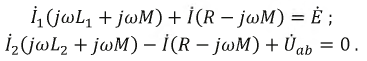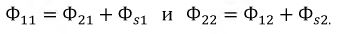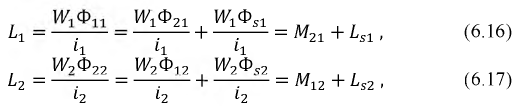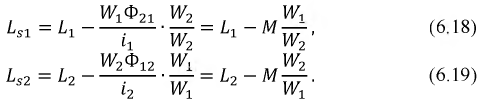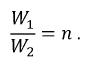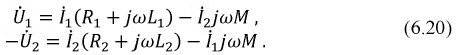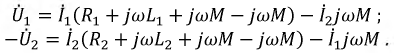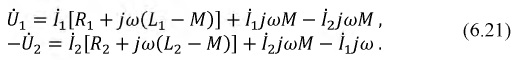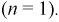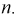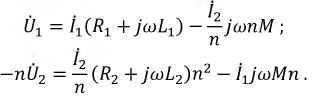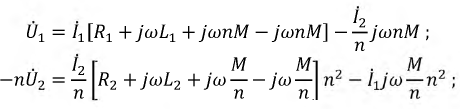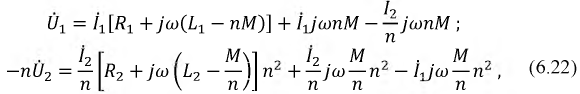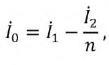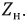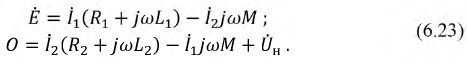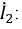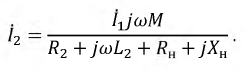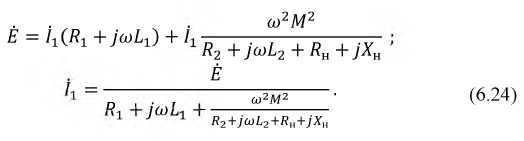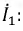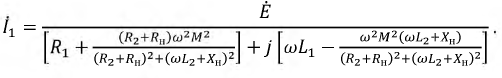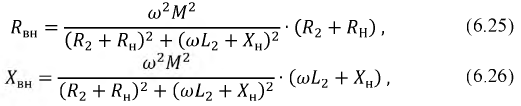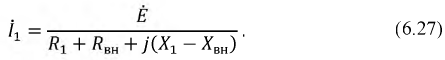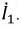Пусть две катушки, обладающие сопротивлениями R1 и R2 , индуктивностями L1 и L2 и взаимной индуктивностью M, соединены последовательно (рис. 30.1).
Рис. 30.1 — Последовательное состояние индуктивно связанных элементов
Возможны два вида их соединения – согласное и встречное. Если считать, что звездочками отмечены начала обмоток, то при согласном включении начало второй подключается к концу первой (рис. 30.1, а). Токи в обеих катушках направлены одинаково относительно одноименных зажимов: от начала к концу. При встречном включении катушек конец второй присоединяется к концу первой (рис. 30.1, б).
Напряжение на каждой из катушек содержит три составляющих: падение напряжения на активном сопротивлении, напряжение самоиндукции и напряжение взаимной индукции:
Последние имеют одинаковые знаки при согласном включении и разные при встречном. Напряжение на входе цепи равно сумме этих двух напряжений:
Входное комплексное сопротивление цепи получим из совместного рассмотрения трех последних уравнений:
где Z1 и Z2 – комплексные сопротивления катушек, а ZM – комплексное сопротивление взаимной индукции:
Из формулы выше вытекают формулы, определяющие общую индуктивность цепи и суммарное индуктивное сопротивление:
Можно определить результирующее индуктивное сопротивление каждой катушки. У первой оно равно X1+-XM. И здесь при согласном включении оно больше чем при встречном. Физически это объясняется тем, что в первом случае магнитный поток, охватывающий каждую катушку, больше чем во втором; например, для первой катушки ФIсогл=Ф1+Ф21, а ФIвстр=Ф1-Ф21. Вследствие этого ЭДС электромагнитной индукции, оказывающая току индуктивное сопротивление, при согласном включении больше, чем при встречном.
На рис. 30.1 изображены векторные диаграммы, построенные по уравнениям (30.1) и (30.2).
Рис. 30.2 — Векторные диаграммы последовательной цепи при согласном (а) и встречном (б) включениях
При встречном включении возможен так называемый «емкостный» эффект, когда у одной из катушек напряжение на зажимах отстает по фазе от тока (напряжение на рис. 30.1, б). Это имеет место, когда индуктивность катушки меньше величины взаимной индуктивности. В этом случае результирующая индуктивность рассматриваемой катушки (с учетом взаимной индукции) отрицательна: L2-M
- Последовательное соединение индуктивно связанных катушек в синусоидальном режиме
- Цепи с взаимной индукцией
- Последовательное и параллельное соединения с взаимной индукцией
- Расчет сложных цепей с взаимной индукцией
- Трансформатор без стального сердечника
- Векторная диаграмма трансформатора
- Линейная теория катушки индуктивности со стальным сердечником
- Резонанс в двух индуктивно связанных цепях
- Электрические цепи с взаимной индуктивностью
- Воздушный трансформатор
- Цепи со взаимной индуктивностью
- ЭДС взаимоиндукции
- Расчет цепей при наличии взаимной индуктивности
- Последовательное встречное включение индуктивно связанных катушек
- Параллельное согласное включение индуктивно связанных катушек
- Параллельное встречное включение индуктивно связанных катушек
- Расчет разветвлённых цепей при наличии взаимной индуктивности
- Эквивалентная замена индуктивных связей
- Линейный (воздушный) трансформатор
- Вносимое сопротивление трансформатора
- 🔥 Видео
Видео:Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Последовательное соединение индуктивно связанных катушек в синусоидальном режиме
Пусть имеется неразветвленная цепь, содержащая две индуктивно связанные катушки. Заданы собственные индуктивности катушек L< и 12; коэффициент взаимной индукции М; сопротивления Rv Rv учитывающие резистивные потери. Источник создает синусоидальное напряжение,</ вх — его комплекс действующего значения.
Возможны два случая соединения связанных катушек в последовательной цени:
- • согласное включение, когда ток в катушках направлен одинаково относительно одноименных зажимов;
- • встречное включение, при котором ток в катушках различным образом ориентирован относительно одноименных зажимов.
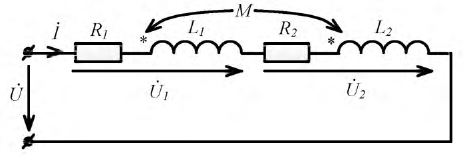
Согласное включение индуктивно связанных катушек (рис. 6.4, а). Для цепи, показанной на рис. 6.4, а, справедливо уравнение по второму закону Кирхгофа
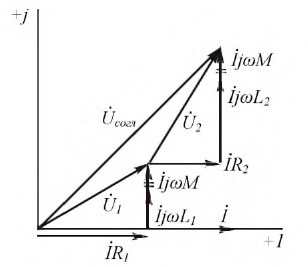
Уравнению (6.13) на комплексной плоскости соответствует векторная диаграмма, представленная на рис. 6.4, 6. Векторы U< и 1)2 на рис. 6.4, 6 изображают полные напряжения на каждой катушке в отдельности.

Рис. 6.4. Последовательное соединение индуктивно связанных катушек,
а — символическая модель цепи; 6 — векторная диаграмма
Комплексное входное сопротивление цепи, показанной на рис. 6.4, а, по отношению к зажимам источника, Zcorri, в соответствии с уравнением (6.13) равно
где Rcorjl = R< + R2 — резистивная составляющая комплекса Zcorjl; Хсогл = = co(Lj + L2 + 2М) — его реактивная составляющая.
Таким образом, наличие индуктивной связи при согласном последовательном соединении катушек приводит к увеличению реактивной составляющей полного комплексного входного сопротивления.
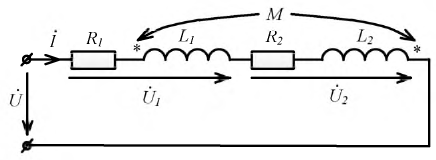
Встречное включение индуктивно связанных катушек (рис. 6.5, а). В уравнение по второму закону Кирхгофа для цепи, показанной на рис. 6.5, а, на-

Рис. 65. Последовательное соединение двух индуктивно связанных катушек,
а — символическая модель цепи; б — векторная диаграмма
пряжения взаимной индукции войдут с противоположным по отношению к напряжениям самоиндукции знаком:
Из последнего уравнения комплексное входное сопротивление цепи, показанной на рис. 6.5, а (обозначено ZBCTp), равно
В выражении (6.15) приняты обозначения: /?встр = /?, + R2 — резистивная составляющая комплекса ZBCTp; Хвстр = (o(L< + L2 — 2М) — реактивная состав- ляющая Znnv.
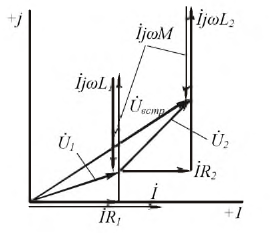
Следовательно, индуктивная связь при встречном включении ведет к уменьшению реактивной составляющей входного сопротивления цепи. При этом необходимо иметь в виду, что так как (L, + L.,) > 2М, то Хвстр не может быть отрицательным. Это означает индуктивный характер полного входного сопротивления последовательного соединения индуктивно связанных катушек независимо от способа включения. Это отражено на векторных диаграммах рис. 6.4, б и 6.5, б, построенных для случаев последовательного соединения индуктивно связанных катушек. 11а обеих диаграммах вектор тока / отстает от вектора входного напряжения.
В соответствии с соотношениями (6.14) и (6.15) /?встр = /?согл; Хвстр ВХ Ш
С учетом выражений Хсогл = со/., + coL2 + 2соМ и Хвстр = сoLx + сoL2 — 2соМ величина сопротивления взаимной индукции равна
а искомый коэффициент взаимной индукции при со = 1000 рад/с равен
Видео:Последовательное соединение RLC элементов в цепи синусоидального токаСкачать

Цепи с взаимной индукцией
Содержание:
Цепи с взаимной индукцией:
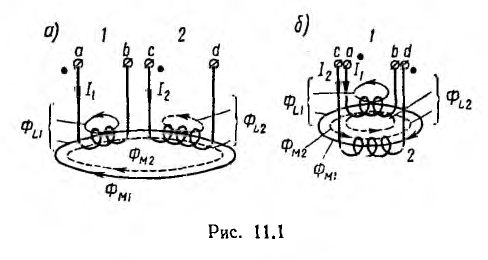
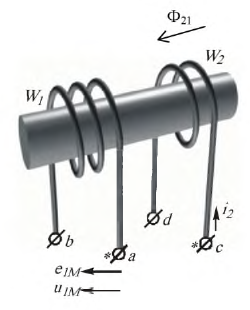
При рассмотрении цепей, отдельные ветви которых связаны между собой взаимоиндуктивкостью М , нужно ввести понятие об одноименных зажимах контуров. Зажимы двух контуров называются одноименными, если при одинаковом направлении токов относительно этих зажимов магнитные потоки самоиндукции ФL и взаимоиндукции ФM в каждом контуре совпадают по направлению. Одноименность зажимов контуров, например катушек, зависит от их взаимного расположения и направления намотки.
Из рис. 11.1, а, например, видно, что в катушках 1 и 2 с одинаковым направлением намотки одноименными являются зажимы а и b (обозначены точками), а также зажимы b и d. Если сдвинуть катушку i в положение, показанное на рис. 11.1, б, потоки взаимоиндукции Фм1 и Фм2 при том же направлении токов окажутся направленными навстречу и одноименными должны стать зажимы а и d (соответственно b и с).
Выбирая в обеих катушках положительные направления э. д. е., напряжений и токов относительно одноименных зажимов одинаковыми, при мгновенном значении тока i1 в первом контуре и разомкнутом втором, мгновенные значения э. д. с. самоиндукции eLl и напряжения uLl первой катушки, пренебрегая ее активным сопротивлением:
и аналогично э. д. с. взаимоиндукции еМ2 и напряжение uм2 второй:
Здесь 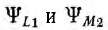
При синусоидальном токе для комплексных величин
Величина ωМ, имеющая размерность сопротивления, называется сопротивлением взаимоиндуктивности хM; комплексное сопротивление взаимоиндуктивности
Видео:Индуктивно связанные цепи │Теория ч.1Скачать

Последовательное и параллельное соединения с взаимной индукцией
При последовательном соединении катушек (рис. 11.2, а и б) ток в них один и тот же, а приложенное напряжение должно преодолеть все э. д. с. и сопротивления цепи. При согласном включении катушек (см, рис. 11.2, а), когда магнитные потоки самоиндукции и взаимоиндукции в обеих катушках направлены одинаково, э. д. с. самоиндукции и взаимоиндукции имеют одинаковые знаки.
При встречном включении катушек (см. рис. 11.2, б) магнитные потоки самоиндукции и взаимоиндукции направлены в противоположные стороны и э. д. с. взаимоиндукции имеет знак, обратный знаку э. д. с. самоиндукции.
Тогда приложенное напряжение при обходе контура по принятому положительному направлению тока
где r1 и r2 — активные сопротивления первой и второй катушек; L1 и L2 — их индуктивности, М — взаимоиндуктивность; верхний знак соответствует согласному, нижний — встречному включению. Для синусоидального напряжения и тока это же соотношение может быть записано в комплексной форме:
Следовательно, результирующие индуктивности катушек и всей цепи при согласном включении
при встречном включении
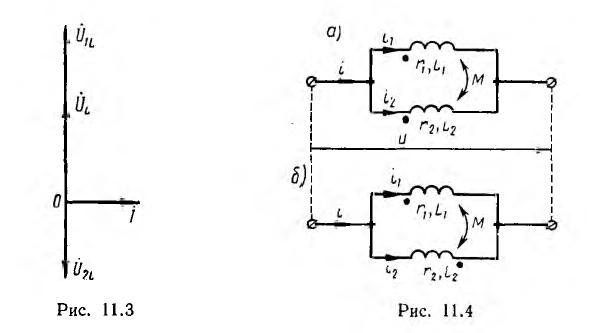
С увеличением М, например при сближении катушек, результирующие индуктивности при согласном включении увеличиваются, при встречном — уменьшаются. При М > L2 результирующая индуктивность L2 второй катушки при встречном включении становится отрицательной. Это значит, что вектор индуктивного напряжения U2L этой катушки получает направление, противоположное векторам индуктивного напряжения UlL первой катушки и UL всей цепи; при этом, очевидно, UlL > U2L и UlL > UL (рис. 11.3). Таким образом, вектор U2L отстает по фазе от вектора тока I на π/2, а на первом участке возникает повышенное напряжение, как будто вместо второй катушки включен конденсатор; это может быть названо случаем ложной емкости. При этом цепь в целом носит индуктивный характер.
Из выражений для результирующих индуктивностей всей цепи для согласного L’ и встречного L» включения можно вычислить взаимоиндуктивность
В других схемах включения катушек, связанных взаимоиндукцией, токи в них в общем случае сдвинуты по фазе; следовательно, часть периода потоки самоиндукции и взаимоиндукции в обеих катушках будут согласными, остальную часть — встречными. Однако принимается, что включение является согласным, если относительно одноименных зажимов совпадают выбранные положительные направления токов.
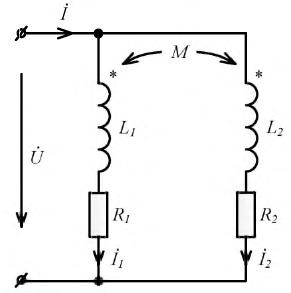
При параллельном соединении катушек (рис. 11.4) их напряжение одинаково. Тогда уравнения равновесия напряжений для первой и второй катушек, соответственно, для мгновенных значений и комплексов имеют вид:
Здесь верхний знак относится к согласному включению (рис. 11.4, а), а нижний — к встречному (рис. 11.4, б).
Если пренебречь активными сопротивлениями катушек, из этих уравнений вытекает, что
Здесь 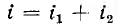
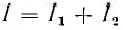
Стедовательно, результирующие индуктивности первой и второй катушек и всей цепи при согласном и встречном включении будут:
Пусть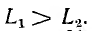
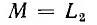
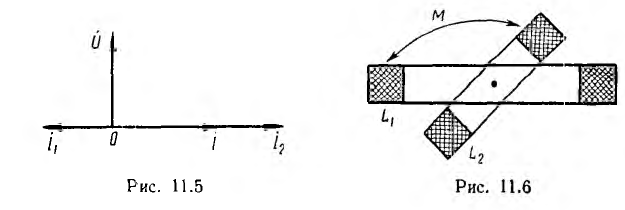
бесконечности; это значит, что э. д. с. взаимоиндукции уравновешивает приложенное напряжение, и ток первой катушки становится равным нулю. При М > L2 имеет место явление ложной емкости: индуктивность L1 становится отрицательной, и вектор тока I1 этой катушки получает направление, противоположное векторам тока I2 второй катушки и I всей цепи (рис. 11.5); вектор ft опережает по фазе вектор напряжения U на π/2, как будто вместо первой катушки включен конденсатор, при этом, очевидно,
Для плавного изменения индуктивности применяют вариометры, состоящие из двух катушек. Меньшая катушка помещена внутри большей и может поворачиваться (рис. 11.6). При совпадении их осей взаимоиндуктивность максимальна: М = Мmах. При повороте М. уменьшается и при прямом угле между осями М= 0. Соединяя катушки параллельно и последовательно, можно получить плавное вменение результирующей индуктивности в пределах от минимального значения при параллельном встречном соединении до максимального при последовательном согласном включении, т. е. от
Если уравнять ее максимальное значение при параллельном согласном включении с минимальным значением при последовательном встречном включении, то
Расчет сложных цепей с взаимной индукцией
Расчет сложных цепей со взаимной индукцией можно вести символическим методом по законам Кирхгофа, так как последние справедливы для любых цепей, но в уравнениях по второму закону Кирхгофа в выражения для напряжений катушек должны быть добавлены комплексные напряжения взаимной индукции вида ± 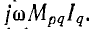
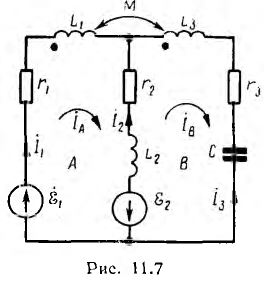
В качестве примера приведена система уравнений, составленных по первому и второму законам Кирхгофа для цепи рис. 11.7 в соответствии с указанными на схеме положительными направлениями э. д. с. и одноименными зажимами, а также выбранными направлениями токов ветвей и обхода контуров:
Для расчета цепей со взаимной индукцией применим также метод контурных токов, так как его вывод был основан на втором законе Кирхгофа, учитывающем э. д. с. взаимной индукции. Уравнения для контурных токов получают вид:
где МAв — взаимоиндуктивность катушек контуров А и В и т. п.. а знак выбирается соответственно сказанному выше. Сопротивление взаимной индукции удобно добавить к взаимным сопротивлениям контуров:
При этом правило знаков изменяется на обратное: при совпадении направлений обхода катушки контура A и тока в катушке контура В у комплекса 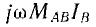
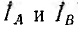
Метод наложения, основанный на линейности уравнений, составленных по законам Кирхгофа, также применим, так как и при наличии взаимной индукции уравнения остаются линейными. Это же относится к методу эквивалентного источника энергии при условии, что ток или напряжение определяются для ветви, не связанной взаимной индукцией с остальной частью цепи.
Метод узловых напряжений для цепей со взаимной индукцией неприменим, так как его вывод основан на первом законе Кирхгофа, который не позволяет непосредственно учесть э. д. с. взаимной индукции. В общем случае цепей со взаимной индукцией неприменим и метод преобразования, так как он основан на использовании кроме второго, также и первого закона Кирхгофа.
Трансформатор без стального сердечника
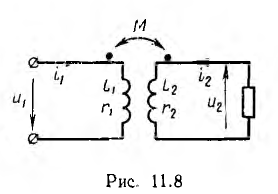
Широкое применение в электротехнике имеет трансформатор — статическое устройство, предназначенное для преобразования величины переменных напряжений и токов. В простейшем случае он не имеет ферромагнитного сердечника и представляет собой две катушки с индуктивной связью (рис. 11.8); такие трансформаторы применяются в радиотехнике.
Напряжение их источника приложено к первичной катушке трансформатора, к вторичной катушке подключена нагрузка.
Тогда уравнения по второму закону Кирхгофа для первичной и вторичной цепей при показанных на рис. 11.8 одноименных зажимах и положительных направлениях токов, при которых потоки самоиндукции и взаимоиндукции складываются, получают следующий вид:
где u2 — напряжение на приемнике, a r1, L1, и r2, L2 — сопротивление и индуктивность, соответственно, первичной и вторичной катушек.
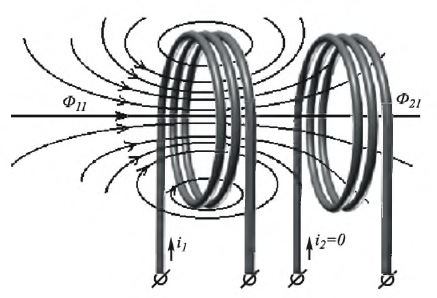
При холостом ходе вторичная катушка разомкнута и ток первичной цепи индуктирует во вторичной э. д. с. взаимоиндукции
При синусоидальном законе изменения величин комплекс э. д. с. холостого хода
При сопротивлении приемника 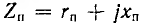
Здесь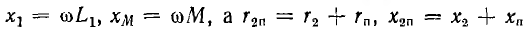
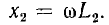
Так как исходные уравнения были составлены в предположении, что потоки, пропорциональные токам, складываются, . знак минус в этом выражении, связывающем комплексы токов I1 и I2, указывает на то, что векторы этих токов составляют тупой угол; в пределе, при 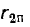
Переход от комплекса вторичного тока к его действующему значению дает:
откуда может быть определен коэффициент трансформации тока
Из этих соотношений видно, что коэффициент трансформации тока не является постоянной величиной, а зависит от сопротивления приемника. Можно показать, что коэффициент трансформации напряжения 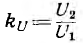
После подстановки значения I2 в первое уравнение трансформатора получается выражение первичного тока:
откуда видно, как будет изменяться ток I1 при изменении сопротивления приемника.
В знаменателе выражения для I2 стоит результирующее полное сопротивление цепи, эквивалентной трансформатору. Результирующее активное сопротивление
состоит из суммы активного сопротивления первичной цепи и сопротивления, вносимого вторичной цепью,
Средняя (активная) мощность, потребляемая трансформатором,
т. е. равна сумме мощностей первичной и вторичной цепи, а к. п. д. трансформатора
Результирующее реактивное сопротивление
состоит из разности реактивного сопротивления первичной цепи х1 и сопротивления x2π вносимого вторичной цепью. При индуктивном характере нагрузки xπ > 0 и вносимое реактивное сопротивление
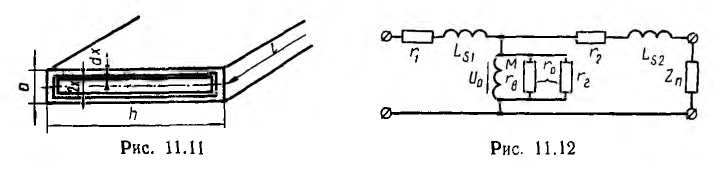
т. е. x2 х2 сопротивление х2 x1 и носит индуктивный характер. При xс U1, что имеет место в трансформаторе, повышающем напряжение. При Ll> М > L2 емкостный характер получает элемент L2— М, что делает возможным соотношение I1 а и длиной l (рис. ll.il), пронизываемом магнитным потоком, изменяющимся по синусоидальному закону. Максимальное значение индукции Вm во всех точках сечения листа принимается одинаковым и сопротивление путей вихревых токов активным, что будет иметь место при пренебрежении размагничивающим действием вихревых токов, т. е. магнитным поверхностным эффектом .
Элементарный контур вихревого тока в виде полого цилиндра высотой l с прямоугольным основанием, имеющим длину 2х, ширину, принимаемую равной h, и толщину стенки dx, пронизывается магнитным потоком, максимальное значение которого
Действующее значение э. д. е., индуктируемой в элементарном контуре,
Активное сопротивление элементарного контура
Тогда мощность, расходуемая в элементарном контуре на вихревые токи,
Мощность, расходуемая во всем листе,
где V = hla — объем листа. Отсюда видно, что потери 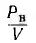
В эквивалентной схеме трансформатора необходимо учесть потери на вихревые токи добавлением ветви, потребляющей ту же мощность. Для этого дополнительное активное сопротивление rB надо включить на напряжение U0 намагничивающей ветви М (рис. 11.12 для трансформатора с ω1= ω2= ω), так как тогда потребляемая им мощность РB будет находиться в квадратичной зависимости от индукции и частоты, как и потери на вихревые токи:
Величина сопротивления rв должна быть такой, чтобы потери Р’в нем равнялись потерям Рв в стали на вихревые токи:
Oткуда
где V, S и b — объем, сечение и средняя длина магнитопровода.
Мощность потерь на гистерезис Рг при частоте f легко получить из формулы Штейнмеца для энергии Wr, затраченной на один цикл перемагничивания:
где коэффициент η зависит от материала, а V — объем магнитопровода. Линейная зависимость этих потерь от частоты в отличие от квадратичной зависимости потерь на вихревые токи может быть использована для разделения суммарных потерь в стали, если они известны для двух частот при одной и той же индукции Вm.
В схеме, эквивалентной трансформатору, потери Рг на гистерезис учитываются сопротивлением 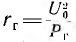
Величина rr определяется аналогично из равенства потерь в сопротивлении и в стали. Если принять последние пропорциональными 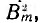
откуда
т. е., помимо конструктивных данных, гг зависит от частоты.
Обычно сопротивления rв и rr объединяются в сопротивление ветви потерь в стали 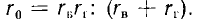
Специальные электротехнические стали с малыми удельными потерями на гистерезис и вихревые токи имеют толщину от 0,5 до 0,1 мм, более тонкие листы приходится применять при повышенной частоте. В радиоэлектронике и вычислительной технике применяются также сердечники из спрессованной смеси ферромагнитного порошка с изолирующим материалом и из ферритов, получаемых спеканием окислов магнитных и немагнитных материалов.
Векторная диаграмма трансформатора
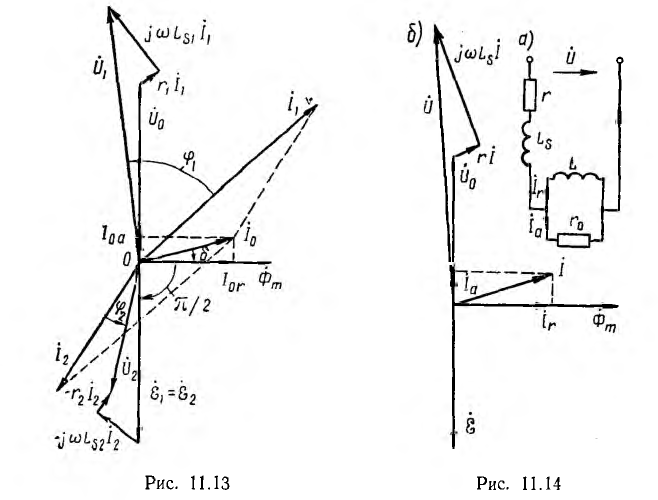
Векторная диаграмма при активно-индуктивной нагрузке для эквивалентной схемы рис. 11.12 и тем самым для трансформатора с ω1= ω2 и со стальным магнитопроводом показана на рис. 11.13 Нелинейность катушек со стальным сердечником при водит к тому, что при синусоидальном напряжении ток i0 намагничивающей ветви будет несинусоидальным Ввиду малости этого тока по сравнению с практически синусоидальными токами i1 и i2 при нагрузке трансформатора можно этим явлением пренебречь, считать все токи синусоидальными и изображать их векторами.
Векторная диаграмма строится в соответствии с положительными направлениями напряжений и токов, принятыми на схеме рис. 11.9. Исходным вектором удобно принять вектор потока взаимоиндукции Фm затем строятся векторы э. д. с. 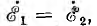
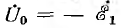
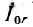
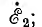
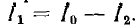
Как видно из диаграммы, в трансформаторе ω1= ω2 напряжения и токи входа и выхода не равны друг другу 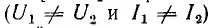
Линейная теория катушки индуктивности со стальным сердечником
При холостом ходе трансформатора, т. е. при разомкнутой вторичной цепи, его эквивалентная схема упрощается (рис. 11.14, а). Очевидно, что трансформатор в этом режиме аналогичен катушке со стальным сердечником, часто применяемой в электротехнике. Тогда схема рис. 11.14, а является также эквивалентной схемой катушки, если намагничивающую ветвь характеризовать не взаимоиндуктивностью М, а равной ей индуктивностью 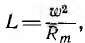
Здесь также часто пренебрегают нелинейностью L и строят векторную диаграмму; по сравнению со случаем нагруженного трансформатора погрешность получается бoльшей.
За исходный вектор векторной диаграммы (рис. 11.14, 6) удобно принять вектср потока Фm в магнитопроводе; вектор э. д. с. 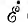
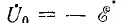
Из-за наличия потерь в меди и стали сдвиг 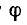
Теория катушки со стальным сердечником, учитывающая нелинейность L.
Резонанс в двух индуктивно связанных цепях
Явление резонанса в связанных цепях широко используется в технике связи, в особенности в радиотехнике — в передающих и приемных устройствах.
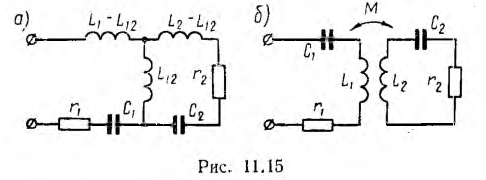
Связанными называются цепи, имеющие общую ветвь в действительной или эквивалентной схеме. Примером может служить индуктивная связь, осуществляемая при помощи общего индуктивного сопротивления (рис. 11.15, а) или путем электромагнитной индукции —трансформаторная связь (рис. 11.15, б). Оба эти вида индуктивной связи будут эквивалентны друг другу, если полные индуктивности Ll и L2 обоих контуров соответственно равны друг другу, a L12= М.
Степень связи цепей характеризуется коэффициентом связи k, который в общем случае представляет собой отношение сопротивления обшей ветви к корню квадратному из произведения одноименных с ним сопротивлений каждого из двух связанных контуров, причем в сопротивление контуров должно быть включено и сопротивление общей ветви. Тогда для простой индуктивной связи (рис. 11.15, а)
для трансформаторной связи (рис. 11.15, б) получается известное выражение
Пусть резонансная частота обеих цепей рис. 11.15, б одинакова:
Если пренебречь активным сопротивлением вторичной цепи (r2 = 0), то из следует, что реактивное сопротивление всей цепи рис. 11.15, б, а следовательно, и эквивалентной ей цепи рис. 11.15, а равно:
При частоте 
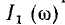
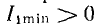
В исследуемой цепи происходит резонанс напряжений, и ток получает максимальное значение при условии х = 0, откуда
Если разделить обе части этого равенства на 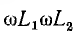
откуда
Следовательно, имеются две частоты, при которых величина I1 максимальна; резонанс напряжений имеет место между левой и разветвленной правой частью схемы рис. 11.15, а; причем для меньшей из этих частот сопротивление левой части эквивалентной схемы носит емкостный характер, а правой — индуктивный, для большей частоты — наоборот.
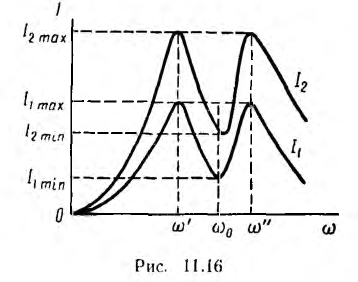
Решение уравнений для этой цепи относительно тока I2 приводит к выводу, что кривая I2 (ω) при Ul = const и малом активном сопротивлении также имеет два максимума при тех же частотах 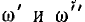
Следовательно, в отличие от кривой I (ω) при U = const для уединенного контура с L и С, имеющей один максимум при последовательном соединении (см. рис. 7.6) или один минимум при параллельном соединении (см. рис. 7.10), резонансные кривые, т. е. частотные характеристики I1(ω) и I2(ω) цепи, состоящей из двух связанных контуров с малым активным сопротивлением, имеют два максимума и один минимум. Выражения для резонансных частот могут служить для нахождения коэффициента связи:
При больших активных сопротивлениях точки резонансов сливаются, и резонансные кривые будут иметь только по одному максимуму.
Видео:Резонанс напряжений в электрической цепиСкачать

Электрические цепи с взаимной индуктивностью
Переменная магнитная связь:
Индуктивность двух взаимосвязанных катушек можно изменить, если кроме магнитной связи эти катушки соединены электрически. Индуктивность таких катушек зависит от их соединения и взаимного расположения относительно друг друга.
Устройство, дающее возможность изменять магнитную связь (коэффициент связи К) двух контуров или катушек, называют вариометром.
Вариометр представляет собой две катушки, одна из которых (2) может поворачиваться внутри неподвижной катушки (1), изменяя
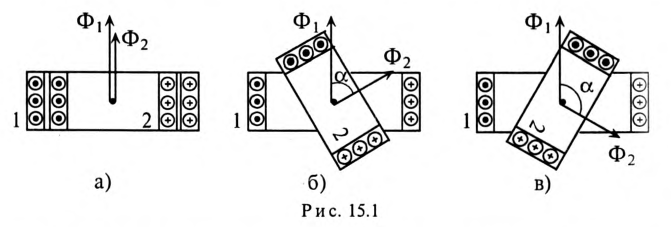
при этом угол между магнитными потоками катушек (рис. 15.1).
В зависимости от взаимного расположения этих катушек различают их согласное и встречное включение.
При согласном включении угол между магнитными потоками катушек 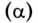
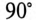
При встречном включении угол между магнитными потоками катушек 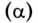
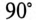
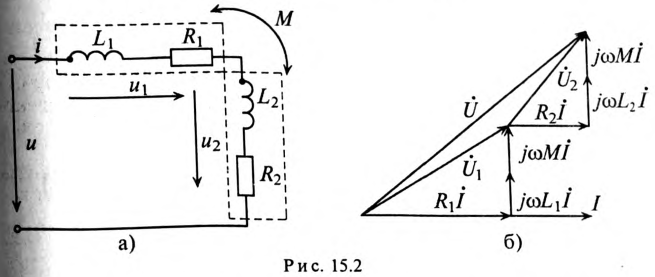
Схема замещения последовательно соединенных катушек вариометра изображена на рис. 15.2а.
При согласном включении катушек суммируются ЭДС самоиндукции, созданные магнитными потоками
Также суммируются ЭДС взаимоиндукции, созданные потоками одной катушки, пронизывающие витки другой катушки:
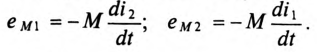
При последовательном соединении катушек (рис. 15.2а)
Составляется уравнение по второму закону Кирхгофа для первой катушки:
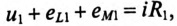
или в комплексной форме
Для второй катушки:
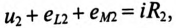
или в комплексной форме
Напряжение, приложенное к последовательно включенным катушкам (входное напряжение), определяется по формуле
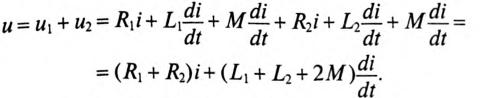
Тогда
Векторная диаграмма цепи при последовательном согласном включении двух катушек показана на рис. 15.2б.
Как следует из (15.3), общая индуктивность двух катушек вариометра при их согласном включении:
Таким образом, при согласном включении катушек ЭДС самоиндукции и взаимоиндукции складываются: (15.1) и (15.2). При встречном включении тех же катушек ЭДС самоиндукции и взаимоиндукции вычитаются:
Для второй катушки:
Тогда напряжение, приложенное к встречно включенным катушкам, определяется выражением
Из выражения (15.7) следует, что общая индуктивность двух катушек вариометра при их встречном включении:
Сравнивая (15.4) и (15.8), видим, что суммарная (эквивалентная) индуктивность двух магнитосвязанных катушек и, следовательно, их индуктивное сопротивление 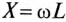
Следовательно, ток магнитосвязанных катушек при согласном включении 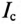
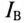
Если обмотку катушки выполнить двумя рядом расположенными изолированными проводами, соединенными электрически с одной стороны (концами или началами), то получится встречное включение, при котором 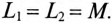
Безындуктивные катушки, намотанные таким двойным проводом, называются бифилярными.
В ряде случаев явление взаимоиндукции бывает полезным (трансформаторы). Иногда это явление бывает нежелательным, например, если параллельно линии электропередачи расположена линия связи.
Воздушный трансформатор
Рассмотрим в качестве примера расчета индуктивно связанных цепей воздушный трансформатор, который состоит из двух индуктивно связанных катушек (обмоток), намотанных одна на другую (рис. 15.3а). 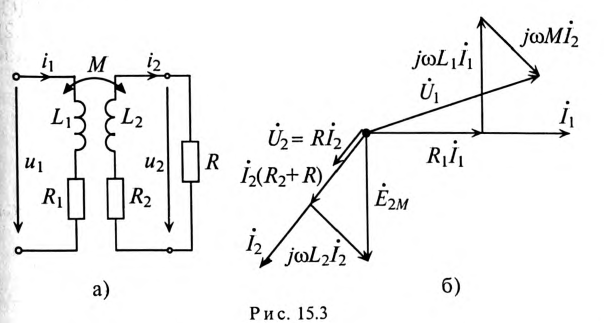
Первичная обмотка трансформатора присоединена к источнику с напряжением 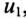
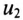
Положительные направления 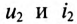
Таким образом, напряжение, приложенное к первичной обмотке трансформатора 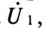
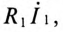
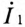
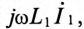
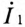
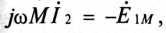
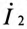
Сопротивление первичной обмотки трансформатора равно
Так как во вторичной цепи отсутствует источник питания, т.е. 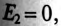
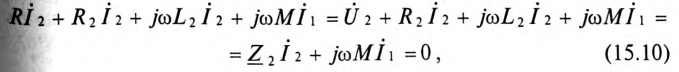
где 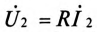
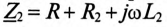
ЭДС взаимоиндукции во вторичной обмотке будет равно
На векторной диаграмме (рис. 15.3б) показано, что 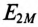
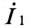
Из выражения (15.11) определяется ток вторичной цепи
Подставив выражение (15.12) для тока 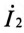
где 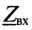
Слагаемое 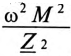
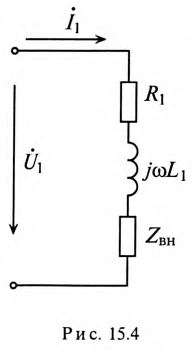
Следовательно, для источника питания нагруженный трансформатор можно представить простой схемой замещения (рис. 15.4).
Тогда по закону Ома
Откуда
Таким образом, при заданных параметрах первичной и вторичной цепей и напряжений источника питания можно рассчитать токи 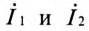
В режиме холостого хода, когда 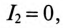
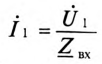
Видео:Векторные диаграммы и коэффициент мощностиСкачать

Цепи со взаимной индуктивностью
Изменение тока в электрической цепи приводит к соответствующему изменению магнитного потока, который, в свою очередь, приводит к появлению ЭДС самоиндукции, обусловленной скоростью изменения потокосцепления
При анализе цепей с синусоидальными токами мы познакомились с явлением самоиндукции, то есть наведением ЭДС в электрической цепи при изменении магнитного потока, обусловленного изменением тока в этой же цепи:
Кроме явления самоиндукции, в электрических цепях возможно возникновение взаимной индукции. Физически это можно объяснить так: изменение тока в одной цепи вызывает изменение величины потокосцепления взаимной индукции в другой и наоборот. В данном случае говорят, что эти цепи индуктивно связаны.
Для исследования данного явления рассмотрим две катушки (рис. 6.1).
Рис. 6.1. Индуктивно связанные катушки
Пусть, например, в катушке 1 протекает ток 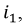
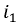
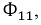
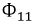
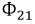
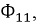
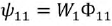
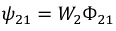
В итоге получим индуктивность первой катушки 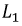
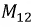
Аналогичная картина могла бы иметь место при протекании тока во второй катушке и отсутствии тока в первой катушке:
Т.к. магнитные свойства среды, заполняющей катушки (воздух), неизменны, то 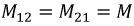
ЭДС взаимоиндукции
На основании закона электромагнитной индукции изменение магнитного потока катушки вызывает ЭДС самоиндукции, которая при линейности катушки может быть определена следующим образом:
В соответствии с законом Ленца (законом электромагнитной инерции) эта ЭДС препятствует изменению потокосцепления. Приложенное к катушке напряжение уравновешивает ЭДС самоиндукции:
Для двух индуктивно связанных катушек изменение тока в одной приводит к изменению величины потокосцепления в другой и, наоборот, при этом:
Величины 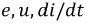
Рис. 6.2. Варианты намотки катушек с согласно направленными магнитными потоками
Рис. 6.3. Варианты намотки катушек со встречно направленными магнитными потоками
Из анализа этих рисунков можно сделать вывод, что направление результирующего магнитного потока определяется не только направлением тока относительно зажимов, но и направлением намотки данных катушек. С целью единообразия в изображении способа соединения катушек прибегают к маркировке их зажимов (точки, звёздочки и т.д.).
Правило. Если относительно маркированных зажимов токи протекают одинаково, то магнитные потоки самоиндукции и взаимной индукции складываются, в противном случае вычитаются. При этом в первом случае говорят о согласном, а во втором — о встречном включении катушек.
Теперь перейдём к вопросу о знаке ЭДС взаимной индукции.
Пусть клеммы первой катушки разомкнуты, а во второй протекает ток указанного направления (рис. 6.4).
Выберем положительные направления ЭДС взаимной индукции и напряжения на её зажимах совпадающими. Ток 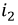
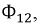
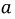
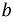
Рис. 6.4. Схема, иллюстрирующая знак ЭДС взаимной индукции
Исходя из выбранных направлений токов, напряжений и ЭДС, можно сделать вывод о том, что наводимая на зажимах первой катушки ЭДС взаимной индукции 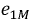
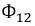
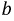
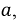
Если 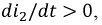
Если 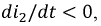
Используя аналогичные рассуждения, можно получить выражение для случая, когда ток, ЭДС и напряжение выбраны неодинаково относительно маркированных зажимов. Например, если изменилось направление тока 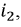
Расчет цепей при наличии взаимной индуктивности
Последовательное согласное включение индуктивно связанных катушек:
Рассмотрение данного вопроса начнём с простейших способов соединения двух индуктивно связанных катушек: последовательного и параллельного. При этом будем использовать комплексный метод расчета.
При согласном способе включения катушек направление тока относительно маркированных зажимов первой и второй катушек одинаковое (рис. 6.5).
Рис. 6.5. Схема последовательного согласного включения двух катушек
Составим уравнение электрического равновесия для данного участка цепи с учётом индуктивной связи по второму закону Кирхгофа:
Используя полученное выражение, построим векторную диаграмму для данного способа соединения (рис. 6.6).
Из полученного выражения следует, что при согласном включении катушек общая индуктивность возрастает на величину 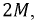
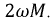
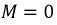
Введём параметр 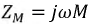
Рис. 6.6. Векторная диаграмма для последовательного согласного включения двух катушек
Последовательное встречное включение индуктивно связанных катушек
При встречном способе включения направление тока относительно маркированных зажимов первой и второй катушек различно (рис. 6.7).
Рис. 6.7. Схема последовательного встречного включения двух катушек
Используя полученные ранее соотношения, можно записать аналогичное уравнение для встречного включения тех же катушек:
Для данного способа включения общая индуктивность уменьшится на 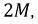
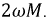
Рис. 6.8. Векторная диаграмма для последовательного встречного включения двух катушек
Параллельное согласное включение индуктивно связанных катушек
Составим систему уравнений для расчета цепи по законам Кирхгофа для схемы рис. 6.9:
Рис. 6.9. Схема параллельного согласного включения двух катушек
Решим полученную систему уравнений относительно токов:
Входная проводимость цепи будет:
В случае, когда взаимная индуктивность 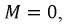
Параллельное встречное включение индуктивно связанных катушек
Для схемы, представленной на рис. 6.9, при встречном включении катушек уравнения для расчета цепи по законам Кирхгофа будут иметь вид:
Решение данной системы:
Входное сопротивление цепи будет:
Соответствующие векторные диаграммы строятся аналогично случаю последовательного соединения данных катушек.
Расчет разветвлённых цепей при наличии взаимной индуктивности
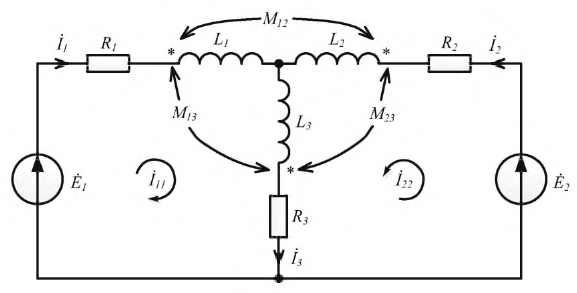
Расчёт разветвлённых цепей при наличии взаимной индуктивности представляется более сложным этапом. Он осуществляется с помощью законов Кирхгофа либо метода контурных токов. Отметим, что метод узловых потенциалов в данном случае неприменим, поскольку токи в ветвях определяются не только разностью потенциалов соседних узлов, но и токами других ветвей, с которыми они связаны индуктивно. Пусть имеются три индуктивно связанные катушки, намотанные на общий сердечник, выполненный из немагнитного материала, и подключённые к двум источникам ЭДС. Получим электрическую схему по рис. 6.10.
Рис. 6.10. Электрическая схема с индуктивно связанными катушками
Проведем расчёт методом контурных токов и составим систему уравнений относительно заданных на схеме контурных токов:
Решив систему, получим:
Эквивалентная замена индуктивных связей
Отличительной особенностью расчёта цепей с взаимной индуктивностью является то, что приходится одновременно учитывать электрические и магнитные связи. Расчёт цепей упростится, если теми или иными методами исключить магнитную связь и свести данную цепь к чисто электрической цепи. Это возможно, если прибегнуть к «развязыванию» магнитных связей, при этом в составе цепи появятся новые дополнительные элементы.
В схеме рис. 6.11 катушки 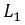
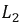
Рис. 6.11. Исходная схема
1. Пусть в узле с катушки соединены разноимёнными зажимами. Составим уравнения по законам Кирхгофа с учётом индуктивной связи:
Преобразуем систему уравнений к следующему виду:
Полученная система описывает схему, представленную на рис. 6.12.
Рис. 6.12. Схема после «развязывания» магнитных связей при соединении катушек в узле разноименными зажимами
2. Если в узле с катушки соединены одноимёнными зажимами, аналогичные рассуждения позволили бы получить другую схему (рис. 6.13).
Рис. 6.13. Схема после «развязывания» магнитных связей при соединении катушек в узле одноименными зажимами
Для обоих случаев определим напряжение 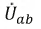
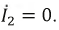
Для катушек, включенных разноименными зажимами, получим:
Для катушек, включенных одноименными зажимами, напряжение определится следующим выражением:
Оставаясь неизменным по модулю, в первом случае напряжение отстаёт на определённый угол, а во втором варианте — опережает ток 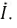
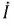
Появление параметра 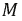
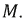
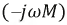
Линейный (воздушный) трансформатор
Воздушный трансформатор (рис. 6.14) является классическим примером линейной цепи, содержащей индуктивную связь.
Рис. 6.14. Схема линейного трансформатора
Полные магнитные потоки, создаваемые токами катушек, можно представить как сумму магнитного потока 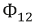
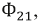
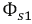
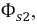
где 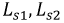
Введем понятие коэффициента трансформации, который представляет собой отношение числа витков первичной обмотки к числу витков вторичной обмотки:
С учетом заданных положительных направлений токов и напряжений в обмотках составим уравнения электрического равновесия для трансформатора, выбрав направление обхода в катушках по часовой стрелке:
Преобразуем данные уравнения следующим образом:
Полученная система уравнений позволяет построить схему замещения воздушного трансформатора, представленную на рис. 6.15.
Рис. 6.15. Схема замещения линейного трансформатора
Индуктивные элементы 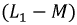

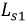
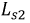
Сопротивления 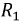
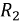
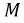
В полученной схеме отсутствует магнитная связь между катушками индуктивности, и теперь они соединены электрически. Однако в подавляющем числе случаев 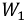
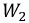
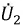
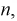
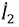
Вновь преобразуем исходные уравнения:
Проведя аналогичного рода преобразования:
и перегруппировав слагаемые:
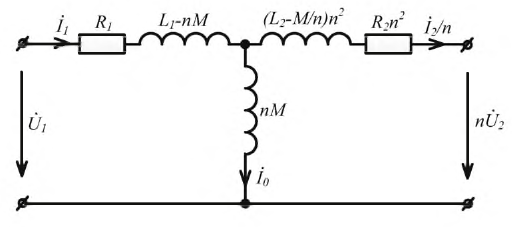
получим систему уравнений (6.22), на основании которых составим схему замещения трансформатора (рис. 6.16).
Рис. 6.16. Схема замещения воздушного трансформатора при неравенстве количества витков в катушках
Ток во вновь образовавшейся ветви:
носит название намагничивающего тока холостого хода трансформатора. Смысловое содержание параметров схемы замещения остается тем же.
Вносимое сопротивление трансформатора
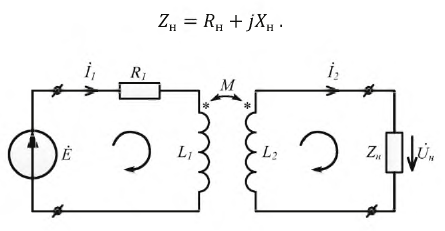
Пусть к выходным зажимам трансформатора по рис. 6.17 подключен приемник с сопротивлением
Рис. 6.17. Схема нагруженного трансформатора
Вновь составим систему уравнений для данной цепи по законам Кирхгофа с учетом выбранного направления обхода:
Выразим из второго уравнения ток 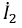
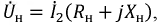
Подставляя его в первое уравнение, получим:
Проведя ряд алгебраических преобразований, получим следующее выражение для тока
где 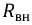
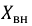
Тогда окончательно имеем:
Физически вносимое сопротивление представляет собой такое сопротивление, включенное последовательно с первичной обмоткой, которое позволяет учесть влияние тока нагрузки 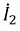
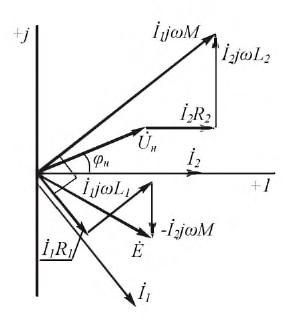
Построим векторную диаграмму трансформатора под нагрузкой.
Пусть в качестве нагрузки используется активно-индуктивный потребитель 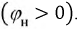
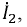
Рис. 6.18. Векторная диаграмма линейного трансформатора под нагрузкой
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Трехфазные цепи
- Периодические несинусоидальные напряжения и токи в линейных цепях
- Нелинейные цепи переменного тока
- Переходные процессы
- Символический метод расчета цепей
- Четырехполюсники
- Линейные диаграммы
- Круговые диаграммы
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🔥 Видео
РЕЗОНАНС ТОКОВ в идеальной и реальной цепях │Теория ч. 1Скачать
Урок 362. Анализ вынужденных электромагнитных колебаний методом векторных диаграммСкачать

Построение векторной диаграммы. Цепь RLCСкачать

Трансформаторы из UPS.Скачать

Векторная диаграмма токов на комплексной плоскости вручнуюСкачать

Тайна Двух ТРАНСФОРМАТОРОВ Единственный грамотный способ их подключения в розеткуСкачать

Параллельное соединение RLC элементов │Переменный токСкачать

Почему UL опережает iL на 90°│Сдвиг фаз между UL и iL│Катушка в цепи переменного токаСкачать

Цепи переменного тока. Комплексные значения сопротивлений, токов и напряжений в цепи. Задача 1Скачать

Урок 359. Конденсатор и катушка индуктивности в цепи переменного тока.Скачать

Векторная диаграмма токов в программе MathcadСкачать

3 9 Индуктивно связанные катушки в цепи переменного синусоидального токаСкачать

Индуктивность катушкиСкачать

Индуктивность. Последовательное подключение.Скачать

2-2. Метод векторных диаграммСкачать