Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Результат
Примеры дифференциальных уравнений
- Простейшие дифференциальные ур-ния 1-порядка
- Дифференциальные ур-ния с разделяющимися переменными
- Линейные неоднородные дифференциальные ур-ния 1-го порядка
- Линейные однородные дифференциальные ур-ния 2-го порядка
- Уравнения в полных дифференциалах
- Решение дифференциального уравнения заменой
- Смена y(x) на x в уравнении
- Другие
Указанные выше примеры содержат также:
- квадратные корни sqrt(x),
кубические корни cbrt(x) - тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
- обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x) - натуральные логарифмы ln(x),
десятичные логарифмы log(x) - гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x) - обратные гиперболические функции:
asinh(x), acosh(x), atanh(x), actanh(x) - число Пи pi
- комплексное число i
Правила ввода
Можно делать следующие операции
2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5
Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)
Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Порядок дифференциального уравнения и его решения, задача Коши
Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную, неизвестную функцию этой переменной и её производные (или дифференциалы) различных порядков.
Порядком дифференциального уравнения называется порядок старшей производной, содержащейся в нём.
Кроме обыкновенных изучаются также дифференциальные уравнения с частными производными. Это уравнения, связывающие независимые переменные 
Примеры дифференциальных уравнений:
(1) 
(2) 
(3) 
(4) 
(5) 
Уравнение (1) — четвёртого порядка, уравнение (2) — третьего порядка, уравнения (3) и (4) — второго порядка, уравнение (5) — первого порядка.
Дифференциальное уравнение n-го порядка не обязательно должно содержать явно функцию, все её производные от первого до n-го порядка и независимую переменную. В нём могут не содержаться явно производные некоторых порядков, функция, независимая переменная.
Например, в уравнении (1) явно нет производных третьего и второго порядков, а также функции; в уравнении (2) — производной второго порядка и функции; в уравнении (4) — независимой переменной; в уравнении (5) — функции. Только в уравнении (3) содержатся явно все производные, функция и независимая переменная.
Решением дифференциального уравнения называется всякая функция y = f(x), при подстановке которой в уравнение оно обращается в тождество.
Процесс нахождения решения дифференциального уравнения называется его интегрированием.
Пример 1. Найти решение дифференциального уравнения 
Решение. Запишем данное уравнение в виде 


Это и есть решение данного дифференциального уравнения. Меняя в нём C, будем получать различные решения. Мы выяснили, что существует бесконечное множество решений дифференциального уравнения первого порядка.
Общим решением дифференциального уравнения n-го порядка называется его решение, выраженное явно относительно неизвестной функции и содержащее n независимых произвольных постоянных, т. е.
Решение дифференциального уравнения в примере 1 является общим.
Частным решением дифференциального уравнения называется такое его решение, в котором произвольным постоянным придаются конкретные числовые значения.
Пример 2. Найти общее решение дифференциального уравнения 

Решение. Проинтегрируем обе части уравнения такое число раз, которому равен порядок дифференциального уравнения.



В результате мы получили общее решение —
данного дифференциального уравнения третьего порядка.
Теперь найдём частное решение при указанных условиях. Для этого подставим вместо произвольных коэффициентов их значения и получим

Если кроме дифференциального уравнения задано начальное условие в виде 


Пример 3. Решить задачу Коши для дифференциального уравнения из примера 1 при условии 
Решение. Подставим в общее решение 

Записываем решение задачи Коши для данного дифференциального уравнения первого порядка:

При решении дифференциальных уравнений, даже самых простых, требуются хорошие навыки интегрирования и взятия производных, в том числе сложных функций. Это видно на следующем примере.
Пример 4. Найти общее решение дифференциального уравнения 
Решение. Уравнение записано в такой форме, что можно сразу же интегрировать обе его части.

Применяем метод интегрирования заменой переменной (подстановкой). Пусть 

Требуется взять dx и теперь — внимание — делаем это по правилам дифференцирования сложной функции, так как x и есть сложная функция («яблоко» — извлечение квадратного корня или, что то же самое — возведение в степень «одна вторая», а «фарш» — самое выражение под корнем):
Возвращаясь к переменной x, получаем:

Это и есть общее решение данного дифференциального уравнения первой степени.
Не только навыки из предыдущих разделов высшей математики потребуются в решении дифференциальных уравнений, но и навыки из элементарной, то есть школьной математики. Как уже говорилось, в дифференциальном уравнении любого порядка может и не быть независимой переменной, то есть, переменной x. Помогут решить эту проблему не забытые (впрочем, у кого как) со школьной скамьи знания о пропорции. Таков следующий пример.
Пример 5. Найти общее решение дифференциального уравнения 
Решение. Как видим, переменная x в уравнении отсутствует. Вспоминаем из курса дифференциального исчисления, что производная может быть записана также в виде 

то есть, в нём в некотором виде появился x.
Теперь вспомнаем одно из свойств пропорции: из пропорции 

то есть в пропорции можно менять местами крайние и средние члены или те и другие одновременно.
Применяя это свойство, преобразуем уравнение к виду

после чего интегрируем обе части уравнения:

Оба интеграла — табличные, находим их:
и получаем решение данного дифференциалного уравнения первого порядка:

Эта статья представила необходимый минимум сведений о дифференциальных уравнениях и их решениях и должна помочь вам уверенно и увлечённо перейти к изучению различных видов дифференциальных уравнений.
📹 Видео
Общее и частное решение дифференциального уравненияСкачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Дифференциальные уравнения. 11 класс.Скачать

Решите уравнение ★ y'-2y=e^(2x) ★ Линейное дифференциальное уравнение 1-го порядкаСкачать
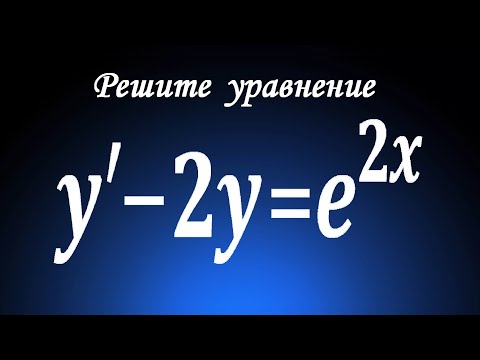
2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Частное решение дифференциального уравнения. 11 класс.Скачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Дифференциальное уравнение от Бермана ★ Решите дифференциальное уравнение 2-го порядка ★ xy''=y'Скачать

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

6. Дифференциальные уравнения, приводящиеся к однороднымСкачать

Как решить дифференциальное уравнение y' = (1 + y) * cos x?Скачать

1. Что такое дифференциальное уравнение?Скачать

Линейное неоднородное дифференциальное уравнение 2 способаСкачать

Дифференциальные уравнения, 7 урок, Дифференциальные уравнения, допускающие понижение порядкаСкачать

ДУ Уравнения, не разрешенные относительно производнойСкачать





