| Название | Автокорреляционная функция это функция от Тип ответа |
| Анкор | ОТветы на синергию |
| Дата | 18.02.2021 |
| Размер | 51.5 Kb. |
| Формат файла |  |
| Имя файла | Эконометрика.doc |
| Тип | Документы #177486 |
 С этим файлом связано 2 файл(ов). Среди них: appresoю.pdf, app.xaml.pdf. Показать все связанные файлы Подборка по базе: Күрделі функция.docx, 1-лекция. Көп айнымалы функциялар.pptx, 1 Клетка.Строение, и их функция.pptx, 4б. L4. corr. 1.Поле, 2.Мин. функция.doc, 5 дәріс.Басқару моделі.Беріліс функциясы.pptx, 2Коммуникативная функция языка.docx, Питон тілі тапсырмалар Циклдер және Функциялар.pdf, Дәріс12 АЖБ Файлдық жүйесінің негізгі функциялары.docx, Алғашқы функция және анықталмаған интеграл..docx, Буль функциялары.docx
Тип ответа: Одиночный выбор Модель авторегрессии первого порядка
Тип ответа: Одиночный выбор Обобщенный метод наименьших квадратов
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор Постоянство дисперсии случайного члена регрессионного уравнения
Тип ответа: Одиночный выбор Отсутствие зависимости между остатками текущих и предыдущих наблюдений
Тип ответа: Одиночный выбор Процесс не является стационарным в широком смысле
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор Показатель, характеризующий тесноту линейной стохастической связи между переменными Явление линейной стохастической связи между переменными Показатель, позволяющий установить факт наличия линейной стохастической связи между переменными
Тип ответа: Одиночный выбор Дисперсии зависимой переменной, объясняемую регрессией в общей ее дисперсии
Тип ответа: Одиночный выбор уравнении регрессии показывает . Процентное изменение зависимой переменной при однопроцентном изменении независимой переменной
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор Статистической значимости модели в целом
Тип ответа: Одиночный выбор Статической зависимости каждого из коэффициентов модели
Тип ответа: Одиночный выбор Определения статической значимости каждого коэффициента уравнения
Тип ответа: Одиночный выбор Наличие линейной зависимости между несколькими объясняющими переменными
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор Дисперсии коэффициентов регрессии
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор Числа структурных коэффициентов над числом приведенных
Тип ответа: Одиночный выбор Максимизирует сумму квадратов остатков
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор О мультиколлинеарности факторов
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор Значение коэффициента равно нулю
Тип ответа: Одиночный выбор С ростом Х происходит убывание У
Тип ответа: Одиночный выбор Объясняющей переменной в i-м наблюдении и прогнозным значением этой переменной
Тип ответа: Одиночный выбор Двухшаговым методом
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор Ранговое условие и порядковое условие со знаком равенства
Тип ответа: Одиночный выбор Коэффициенты множественной детерминации некоторых объясняющих факторов с остальными
Тип ответа: Одиночный выбор Переменной Y в i-м наблюдении и прогнозным значением этой переменной, полученным по выборочной линии регрессии
Тип ответа: Одиночный выбор Классический
Тип ответа: Одиночный выбор Положительные и отрицательные
Тип ответа: Одиночный выбор В три раза
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор Эндогенных переменных минус единица
Тип ответа: Одиночный выбор Отбор факторов, влияющих на результат и выбор вида уравнения
Тип ответа: Одиночный выбор Парные и множественные
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор Необходимым и достаточным
Тип ответа: Одиночный выбор Системы минус единица
Тип ответа: Одиночный выбор Процентное изменение зависимой переменной при однопроцентном изменении независимой переменной
Тип ответа: Одиночный выбор Проверки статистической значимости фактора Можно рассматривать в узком и в широком смысле Характеристика временного ряда, связанная с его стабильностью
Тип ответа: Одиночный выбор Качество уровня регрессии в целом
Тип ответа: Одиночный выбор По нормальному закону
Тип ответа: Одиночный выбор Качество уравнения регрессии в целом
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор Ее математическое ожидание не равно ей
Тип ответа: Одиночный выбор Связь между переменными, сложенная влиянием случайных факторов
Тип ответа: Одиночный выбор Обладают свойством гетероскедастичности
Тип ответа: Одиночный выбор
Тип ответа: Одиночный выбор Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать  Эконометрика, её задача и метод. Эконометрические модели и два принципа их спецификации (стр. 22 )
Это так называемая неограниченная приведённая форма. Структурную форму можно записать следующим образом:
Это так называемая ограниченная приведённая форма, то есть приведённая форма с ограничением на коэффициенты следующего вида: Если задана структурная форма, то всегда можно получить ограниченную приведённую форму (предполагается, что матрица А невырождена). Однако, обратное не всегда возможно, а если возможно, то не всегда однозначно. Структурное уравнение называется идентифицируемым, если его коэффициенты можно выразить через коэффициенты приведённой формы. Если это можно сделать единственным способом, то говорят о точной индентифицируемости, если несколькими способами — о сверхидентифицируемости. В противном случае оно называется неидентифицируемым. Сверхидентифицируемость фактически означает, что на коэффициенты приведённой формы наложены некоторые ограничения (сверхидентифицирующие). В полной приведённой форме участвуют все экзогенные переменные и на коэффициенты не налагается никаких ограничений. Необходимое условие идентифицируемости структурного уравнения (порядковое условие): количество переменныхправой части уравнения должно быть не больше количества всех экзогенных переменных системы. В канонической форме (когда «левой» и «правой» частей нет) данное условие иногда формулируют следующим образом: количество исключенных из данного уравнения экзогенных переменных должно быть не меньше количества включенных эндогенных переменныхуравнения минус единица. Если данное условие не выполнено, то уравнение неидентифицируемо. Если выполнено со знаком равенства, то, вероятно, точно идентифицируемо, иначе — сверхидентифицируема. Достаточное условие идентифицируемости структурного уравнения: ранг матрицы, составленной из коэффициентов (в других уравнениях) при переменных, отсутствующих в данном уравнении, не меньше общего числа эндогенных переменных системы минус единица. Простейшая макроэкономическая (кейнсианская) модель
Здесь C и Y — потребление (потребительские расходы) и доход — эндогенные переменные модели, I — инвестиции — экзогенная переменная модели, b — предельная склонность к потреблению Приведённая форма модели имеет вид:
Величина Можно проверить порядковое условие идентифицируемости. В первом уравнении в правой части 1 эндогенная переменная и нет экзогенных переменных (без учета константы). Всего экзогенных переменных в модели — 1 (тоже без константы). Таким образом, порядковое (необходимое) условие идентифицируемости выполнено. Видно, что приведённая форма является ограниченной с двумя ограничениями 40. Эконометрические модели из одновременных уравнений. Нарушение предпосылки теоремы Гаусса-Маркова о некоррелированности объясняющих переменных и случайных возмущений как источник несостоятельности мнк-оценок параметров (на примере простой кейнсианской модели формирования доходов). Существуют несколько методов вычисления состоятельных оценок параметров линейной модели множественной регрессии в условиях нарушения четвертой предпосылки теоремы Гаусса-Маркова. Наиболее практичный метод — метод применения инструментальных переменных. В его основе лежит понятие инструментальной переменной. Определение. Пусть имеется модель линейной множественной регрессии
в которой объясняющие переменные 1. Существует предел
2. Существует невырожденная матрица:
Из определения следует, что инструментальные переменные в пределе коррелируют с исходными регрессорами Теорема. Процедура 41. Использование инструментальных переменных при идентификации поведенческих уравнений модели в структурной форме. В основе метода применения инструментальных переменных для вычисления состоятельных оценок параметров линейной модели множественной регрессии в условиях нарушения четвертой предпосылки теоремы Гаусса-Маркова лежит понятие инструментальной переменной. Определение. Пусть имеется модель линейной множественной регрессии Yt=a1x1t + a2x2t + akxkt + ut M(ut) = 0; σ2(ut) = σ2u В которой объясняющие переменные коррелируют в пределе со случайными возмущениями ut. Переменные (z1t, z2t,…,zkt) называются инструментальными для модели, приведенной выше, если они соответствуют двум требованиям: Существует невырожденная матрица: Заметим, что инструментальные переменные в пределе коррелируют с исходными регрессорами, но не коррелируют со случайными возмущениями. доставляет состоятельные оценки параметров модели 1. Таким образом, инструментальные переменные используются в косвенном методе наименьших квадратов и двухшаговом методе наименьших квадратов для идентификации поведенческих уравнений модели в их структурной форме. 41.52. Эконометрические модели из одновременных уравнений. Процедура двухшагового метода наименьших квадратов оценивания уравнения модели. Если система одновременных уравнений сверхидентифицируема, то КМНК не используется, так как он не дает однозначных оценок для параметров структурной модели. В этом случае могут использоваться разные методы оценивания, среди которых наиболее распространенным и простым является двухшаговый метод наименьших квадратов (ДМНК). Алгоритм двухшагового метода наименьших квадратов реализуется в четыре этапа. 1. На основе структурной формы системы одновременных уравнений составляется ее приведенная форма. 2. Неизвестные коэффициенты каждого уравнения приведенной формы системы одновременных уравнений оцениваются традиционным методом наименьших квадратов. 3. Рассчитываются значения тех эндогенных переменных, которые выступают в качестве факторных переменных в сверхидентифицированном уравнении. 4. С помощью традиционного метода наименьших квадратов определяются все структурные коэффициенты уравнений системы через предопределенные переменные, входящие в это уравнение в качестве факторов, и значения эндогенных переменных, полученных на предыдущем шаге. Метод получил название двухшагового МНК потому, что МНК используется дважды: на первом шаге при определении приведенной формы модели и на четвертом шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным расчетных значений эндогенных переменных. Видео:Характеристическое уравнение в ДУСкачать  Необходимое условие идентифицируемостиЧтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного. Введем следующие обозначения: М – число предопределенных переменных в модели; m— число предопределенных переменных в данном уравнении; — число эндогенных переменных в модели; Обозначим число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в данное уравнение через Тогда условие идентифицируемости каждого уравнения модели может быть записано в виде следующего счетного правила:
Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема. Рассмотренное счетное правило отражает необходимое, но недостаточное условие идентификации. Достаточное условие идентификации Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного. Целесообразность проверки условия идентификации модели через определитель матрицы коэффициентов, отсутствующих в данном уравнении, но присутствующих в других, объясняется тем, что возможна ситуация, когда для каждого уравнения системы выполнено счетное правило, а определитель матрицы названных коэффициентов равен нулю. В этом случае соблюдается лишь необходимое, но не достаточное условие идентификации. В эконометрических моделях часто наряду с уравнениями, параметры которых должны быть статистически оценены, используются балансовые тождества переменных, коэффициенты при которых равны Изучается модель (одна из версий модели Кейнса): где Первое уравнение – функция потребления, второе уравнение – функция инвестиций, третье уравнение –тождество ВВП. Модель представляет собой систему одновременных уравнений. Проверим каждое ее уравнение на идентификацию. Модель включает три эндогенные переменные Проверим необходимое условие идентификации для каждого из уравнений модели.
Например, первое уравнение содержит две эндогенные переменные Таким образом, Проверим для каждого уравнения достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели.
В соответствии с достаточным условием идентификации ранг матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, должен быть равен числу эндогенных переменных модели без одного. Первое уравнение: матрица коэффициентов при переменных, не входящих в уравнение, имеет вид: Второе уравнение: матрица коэффициентов при переменных, не входящих в уравнение, имеет вид: Таким образом, эта система уравнений является сверхидентифицируемой. 7.5. Методы оценки параметров структурной формы модели Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в литературе получили следующие методы оценивания коэффициентов структурной модели: 1) косвенный метод наименьших квадратов; 2) двухшаговый метод наименьших квадратов; 3) трехшаговый метод наименьших квадратов; 4) метод максимального правдоподобия с полной информацией; 5) метод максимального правдоподобия при ограниченной информации. Рассмотрим сущность некоторых из этих методов. Косвенный метод наименьших квадратов (КМНК) применяется в случае точно идентифицируемой структурной модели. Процедура применения КМНК предполагает выполнение следующих этапов: 1. Для структурной модели строится приведенная форма модели. 2. Для каждого уравнения приведенной формы традиционным МНК оцениваются приведенные коэффициенты 3. На основе коэффициентов приведенной формы находятся путем алгебраических преобразований параметры структурной модели. Двухшаговый метод наименьших квадратов (ДМНК) Если система сверхидентифицируема, то КМНК не используется, ибо он не дает однозначных оценок для параметров структурной модели. В этом случае могут использоваться разные методы оценивания, среди которых наиболее распространенным и простым является двухшаговый метод (ДМНК). Основная идея ДМНК состоит в следующем: · на основе приведенной формы модели получить для сверхидентифицируемого уравнения расчетные значения эндогенных переменных, содержащихся в правой части этого уравнения; · подставляя найденные расчетные значения эндогенных переменных вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Метод получил название двухшагового МНК, ибо дважды используется МНК: · на первом шаге при определении параметров приведенной формы модели и нахождении на их основе оценок расчетных значений эндогенных переменных · на втором шаге применительно к структурному сверхидентифицируемому уравнению, когда вместо фактических значений эндогенных переменных рассматриваются их расчетные значения, найденные на предыдущем шаге. Сверхидентифицируемая структурная модель может быть двух типов: · все уравнения системы сверхидентифицируемы; · система содержит наряду со сверхидентифицируемыми точно идентифицируемые уравнения. Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним можно найти на основе косвенного МНК. Двухшаговый метод, примененный к точно идентифицированным уравнениям дает такой же результат, что и косвенный МНК. Продолжение примера 15. Продолжим рассмотрение примера 15. Система является сверхидентифицируемой: первое уравнение идентифицируемо, а второе уравнение сверхидентифицируемо. Поэтому для определения коэффициентов первого уравнения можно применить косвенный МНК, а для второго уравнении двухшаговый МНК. Построим приведенную форму модели: Исходные данные задачи (в млрд. руб.)
Найдем параметры модели (7.9), применяя МНК к каждому уравнению, используем « Пакет анализа» EXCEL): Каждое уравнение статистически значимо ( На основе уравнений модели (7.10) найдем структурные коэффициенты первого уравнения. Выразим из третьего уравнения (7.10) переменную Так как второе уравнение сверхидентифицировано, то применим двухшаговый МНК. Найдем на основе третьего уравнения (7.10) расчетные значения переменной Получим: В результате получим следующую систему структурных уравнений: Трехшаговый метод наименьших квадратов (ТМНК) Трехшаговый метод наименьших квадратов применяется для оценки параметров системы одновременных уравнений в целом. Сначала к каждому уравнению применяется двухшаговый метод с целью оценить коэффициенты и случайные остатки каждого уравнения. Затем строится ковариационная матрица остатков и проводится ее оценка. После этого для оценивания коэффициентов всей системы применяется обобщенный метод наименьших квадратов. ТМНК является достаточно эффективным, но требует существенно больших вычислительных затрат. Более подробное описание можно найти в работе[1][1] 💥 ВидеоФормула Муавра ➜ Вычислить ➜ (5+5i)⁷Скачать  Изображение комплексных чисел. Модуль комплексного числа. 11 класс.Скачать  Числовые Промежутки — Алгебра 8 класс / Подготовка к ЕГЭ по МатематикеСкачать  Решите уравнение ➜ ДВИ до ЕГЭСкачать  Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать  Числовые промежутки. 6 класс.Скачать  Математика. Линейные диофантовы уравнения с двумя неизвестными. Центр онлайн-обучения «Фоксфорд»Скачать  Что такое математическая последовательность? | Математика | TutorOnlineСкачать  7. ДУ. ЛНДУ с правой частью спец вида (4270 Берман Г.Н)Скачать  Уравнение с комплексными числамиСкачать  ЛОДУ 2 порядка c постоянными коэффициентамиСкачать  МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать  Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать  06. Формула ЭйлераСкачать  ✓ Задача про комплексное число | Ботай со мной #101 | Борис ТрушинСкачать  Алгебра 7 класс. 19 сентября. Числовые промежуткиСкачать  |
.
называется мультипликатором инвестиций (единица увеличения инвестиций приводит к существенно большему изменению дохода).
и 
.
(1)
коррелируют в пределе со случайными возмущениями 
.То есть не выполняется условие состоятельности МНК-оценок параметров модели о том, что существует и равен предел по вероятности: 
). Переменные 
называются инструментальными для модели (1), если они удовлетворяют двум требованиям:
доставляет состоятельные оценки параметров модели (1).
Plimn→∞((1/n)ZTu) = 0
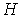— число эндогенных переменных в данном уравнении;
, 
.
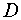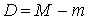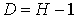
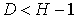
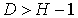
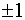. В этом случае, хотя само тождество и не требует проверки на идентификацию, ибо коэффициенты при переменных в тождестве известны, в проверке на идентификацию структурных уравнений системы тождества участвуют..
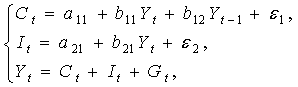(7.8)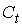
– потребление в период 
; 
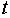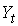– ВВП в период 
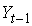— ВВП в период ( 
); 
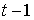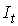– валовые инвестиции в период 
; 
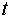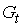– государственные расходы в период 
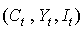и две предопределенные переменные (одна экзогенная переменная –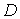 
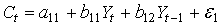
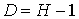
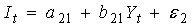
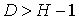
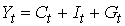
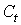и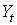 
и одну предопределенную переменную 
.
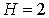; D=2-1=1. Условие условие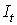 
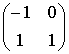. Ее определитель не равен нулю, поэтому ранг матрицы равен 2, т. е равняется числу эндогенных переменных без одного. Достаточное условие идентификации выполняется.
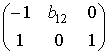. Ранг данной матрицы равен 2, так как существут определитель второго порядка не равный нулю: 
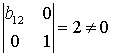. Следовательно, достаточное условие идентификации для данного уравнения также выполняется Но в соответствии с необходимым условием считаем это уравнение сверхидентифицируемым.
.
; 
;
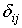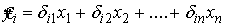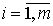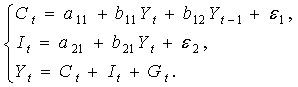
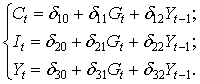(7.9)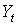
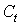
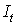
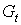
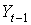
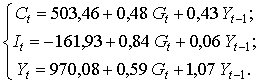(7.10)
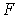– статистики: 
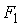=1302,55;
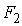=281,956; 
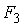=847,65). Коэффициенты детерминации свидетельствуют о хорошей связи между эндогенными и предопределенными переменными: 
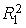=0,9977; 
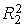=0,989; 
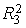=0,996.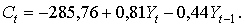
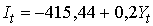4;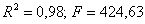 
.