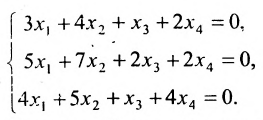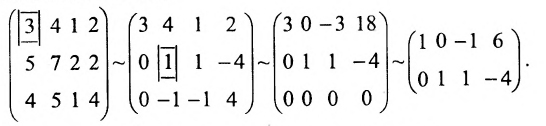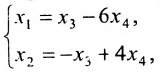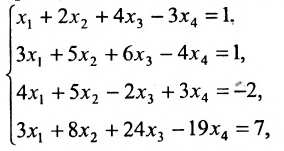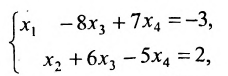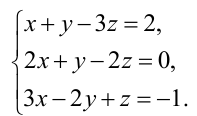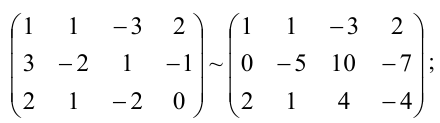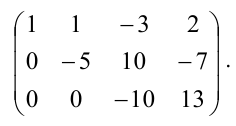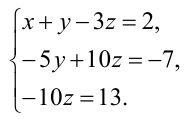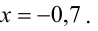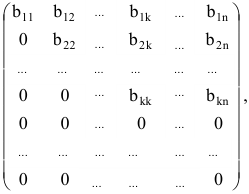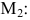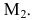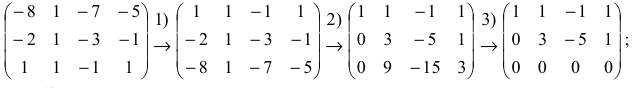В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.
- Общие сведения (определения, условия, методы, виды)
- Ранг матрицы и его свойства
- Системы линейных алгебраических уравнений
- Правило Крамера
- Условие совместности системы линейных уравнений
- Метод Гаусса — определение и вычисление с примерами решения
- Алгоритм решения системы m линейных уравнений с n неизвестными методом Гаусса
- Исследование совместности и определённости системы. Теорема Кронекера-Капелли
- Однородные системы линейных уравнений
- Фундаментальная система решений. Общее решение неоднородной системы линейных уравнений
- Определение метода Гаусса
- Вычисление метода Гаусса
- 🔍 Видео
Видео:Исследование систем линейных уравнений на совместностьСкачать

Общие сведения (определения, условия, методы, виды)
Системы линейных алгебраических уравнений с n неизвестными могут иметь:
- единственное решение;
- бесконечное множество решение (неопределенные СЛАУ);
- ни одного решения (несовместные СЛАУ).
Пример 1
Система x + y + z = 1 2 x + 2 y + 2 z = 3 не имеет решений, поэтому она несовместна.
Система x + y = 1 2 x + 7 y = — 3 имеет единственное решение x = 2 ; y = 1 .
Система x + y = 1 2 x + 2 y = 2 3 x + 3 y = 3 имеет бесконечное множество решений x = t y = 1 — t при — ∞ t ∞ .
Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:
- Совместна ли система?
- Если система совместна, то, какое количество решений она имеет — одно или несколько?
- Как найти все решения?
Если система малоразмерна при m = n , то ответить на поставленные вопросы можно при помощи метода Крамера:
- если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
- если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
- если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.
Видео:Совместные и несовместные, определенные и неопределенные системы линейных уравненийСкачать

Ранг матрицы и его свойства
Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.
Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда
В математике выделяют следующие подходы к определению ранга матрицы:
- при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
- при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
- при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.
Обозначение ранга матрицы: r ( A ) , r g ( A ) , r A .
Свойства ранга матрицы:
- квадратная невырожденная матрица обладает рангом, который отличается от нуля;
- если транспонировать матрицу, то ранг матрицы не изменяется;
- если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
- при удалении нулевого столбца или строки ранг матрицы не изменяется;
- ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
- при умножении все элементов строки/столбца на число k н е р а в н о н у л ю ранг матрицы не изменяется;
- ранг матрицы не больше меньшего из ее размеров: r ( А ) ≤ m i n ( m ; n ) ;
- когда все элементы матрицы равны нулю, то только тогда r ( A ) = 0 .
Пример 2
А 1 = 1 1 1 2 2 2 3 3 3 , B 1 = 1 0 0 0 0 0
r ( A 1 ) = 1 , r ( B 1 ) = 1
А 2 = 1 2 3 4 0 5 6 7 0 0 0 0 ; В 2 = 1 1 3 1 2 1 4 3 1 2 5 0 5 4 13 6
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Системы линейных алгебраических уравнений
Системой линейных алгебраических уравнений с неизвестными называется система уравнений вида
Числа называются коэффициентами системы ; — свободными членами , — неизвестными . Количество уравнений в системе может быть меньше, больше или равно числу неизвестных.
Решением системы называется упорядоченная совокупность чисел такая, что после замены неизвестных соответственно числами каждое уравнение системы превращается в верное числовое равенство. Система называется совместной , если она имеет хотя бы одно решение. Если система не имеет ни одного решения, то она называется несовместной .
Система (5.1) называется однородной , если все свободные члены равны нулю:
В отличие от однородной, систему общего вида (5.1) называют неоднородной .
Систему (5.1) принято записывать в матричной форме. Для этого из коэффициентов системы составляем матрицу системы
свободные члены записываем в столбец свободных членов
а неизвестные — в столбец неизвестных
Матричная запись неоднородной системы уравнений (5.1) имеет вид
Матричную запись (5.3) системы уравнений можно представить в эквивалентной форме
Тогда решение системы представляется столбцом и удовлетворяет равенству
т.е. столбец свободных членов является линейной комбинацией столбцов матрицы системы.
Относительно системы уравнений нас интересуют ответы на следующие вопросы:
1. Совместна система или нет?
2. Если система совместна, то имеет ли она единственное решение или нет?
3. Если решение единственное, то как его найти?
4. Если система имеет бесконечно много решений, то какова структура множества решений?
5. Как в бесконечном множестве решений системы определить одно решение, наилучшее с практической точки зрения?
6. Если система несовместна, то как определить ее приближенное решение?
Видео:Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Правило Крамера
Рассмотрим случай, когда число уравнений равно числу неизвестных , т.е. систему
где матрица системы — квадратная n-го порядка:
Ее определитель обозначим
Теорема 5.1 (правило Крамера). Если определитель матрицы системы линейных уравнений с неизвестными отличен от нуля, то система имеет единственное решение, которое находится по формулам
где — определитель матрицы, полученной из матрицы системы заменой i-го столбца столбцом свободных членов, т.е.
В самом деле, рассмотрим систему (5.6) как матричное уравнение . Так как определитель матрицы отличен от нуля, по теореме 4.2 заключаем, что матричное уравнение имеет единственное решение:
где — обратная матрица. Запишем i-й элемент столбца , учитывая, что в i-й строке присоединенной матрицы стоят алгебраические дополнения i-го столбца матрицы
Заметим, что в скобках записано разложение определителя по i-му столбцу, т.е. , что и требовалось доказать.
1. На практике при больших правило Крамера не применяется, так как вычисление определителя n-го порядка требует большого числа арифметических операций. Поэтому применяются более экономичные алгоритмы. Обычно, правило Крамера используется, когда нужно найти только несколько неизвестных (например, одну) среди многих. В теоретических исследованиях правило Крамера незаменимо и используется весьма продуктивно.
2. Если и хотя бы один определитель , то система несовместна. Если , то возможны два случая: либо система несовместна, либо имеет бесконечно много решений.
Пример 5.1. Решить систему линейных уравнений с помощью правила Крамера
Решение. Составим матрицу системы . Вычислим ее определитель
Так как определитель отличен от нуля, система имеет единственное решение (см. теорему 5.1). Находим определители и неизвестные
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Условие совместности системы линейных уравнений
Рассмотрим систему (5.3) линейных уравнений с неизвестными. Составим блочную матрицу, приписав к матрице справа столбец свободных членов. Получим расширенную матрицу системы :
Эта матрица содержит всю информацию о системе уравнений, за исключением обозначений неизвестных.
Теорема 5.2 Кронекера-Капелли. Система совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы: .
Необходимость следует из равенства (5.5) и следствия 1 теоремы 3.3. Если система имеет решение, то столбец свободных членов есть линейная комбинация столбцов матрицы системы. Поэтому при вычеркивании столбца Ь из расширенной матрицы ее ранг не изменяется. Следовательно, .
Для доказательства достаточности нужно использовать теорему о базисном миноре. Из равенства следует, что базисный минор матрицы является базисным минором расширенной матрицы . Поэтому столбец является линейной комбинацией столбцов базисного минора матрицы , а, значит, и всех столбцов матрицы . Следовательно, существуют числа , удовлетворяющие условию (5.5), т.е. система совместна.
Замечание 5.2. Теорема Кронекера-Капелли дает лишь критерий существования решения системы, но не указывает способа отыскания этого решения.
Пример 5.2. Определить, имеет ли система уравнений решения
Решение. Составим матрицу системы и расширенную матрицу системы
Ранг матрицы равен 2, так как она имеет не равные нулю миноры второго порядка и третья строка этой матрицы равна сумме первых двух строк. Следовательно, третью строку можно вычеркнуть, при этом ранг матрицы не изменится. Ранг расширенной матрицы равен трем, так как она имеет не равный нулю минор третьего порядка, например, минор, составленный из первого, второго и последнего столбцов расширенной матрицы
Следовательно, . Поэтому система несовместна (не имеет решений).
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Метод Гаусса — определение и вычисление с примерами решения
Содержание:
Базисные и свободные переменные:
Пусть задана система
Элементарными преобразованиями системы линейных уравнений называются следующие преобразования:
- исключение из системы уравнения вида
- умножение обеих частей одного из уравнений системы на любое действительное число
;
- перестановка местами уравнений системы;
- прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число не равное нулю.
Элементарные преобразования преобразуют данную систему уравнений в эквивалентную систему, т.е. в систему, которая имеет те же решения, что и исходная.
Для решения системы т линейных уравнений с т неизвестными удобно применять метод Гаусса, называемый методом последовательного исключения неизвестных, который основан на применении элементарных преобразований системы. Рассмотрим этот метод.
Предположим, что в системе (6.1.1)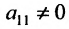
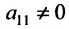
На первом шаге метода Гаусса исключим неизвестное 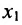
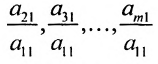
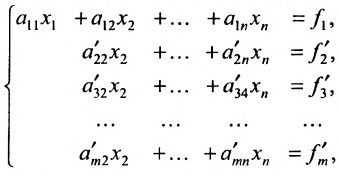
в которой коэффициенты 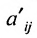
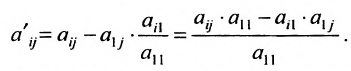
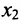
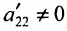
чтобы это условие было выполнено). Для исключения неизвестного 
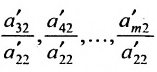
в которой коэффициенты 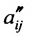
Продолжая аналогичные преобразования, систему (6.1.1) можно привести к одному из видов:
Совокупность элементарных преобразований, приводящих систему (6.1.1) к виду (6.1.4) или (6.1.5) называется прямым ходом метода Гаусса.
Отметим, что если на каком-то шаге прямого хода метода Гаусса получим уравнение вида:
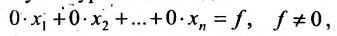
Итак, предположим, что в результате прямого хода метода Гаусса мы получили систему (6.1.4), которая называется системой треугольного вида. Тогда из последнего уравнения находим значение 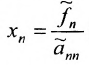
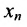
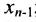
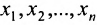
Если же в результате прямого хода метода Гаусса мы получим систему (6.1.5), которая называется системой ступенчатого вида, то из последнего уравнения этой системы находим значение неизвсстного 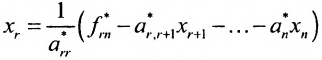
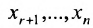
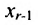
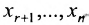
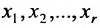
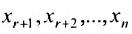
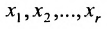
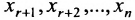
Таким образом, если система (6.1.1) путём элементарных преобразований приводится к треугольному виду (6.1.4), то она имеет единственное решение, если же она приводится к системе ступенчатого вида (6.1.5), то она имеет бесконечное множество решений. При этом неизвестные 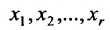
Практически удобнее преобразовывать не саму систему уравнений (6.1.1), а расширенную матрицу системы, соединяя последовательно получающиеся матрицы знаком эквивалентности
Формализовать метод Гаусса можно при помощи следующего алгоритма.
Видео:Решение системы уравнений методом ГауссаСкачать

Алгоритм решения системы m линейных уравнений с n неизвестными методом Гаусса
1. Составьте расширенную матрицу коэффициентов системы уравнений так, чтобы 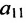
2. Выполните первый шаг метода Гаусса: в первом столбце начиная со второй строки, запишите нули, а все другие элементы вычислите по формуле
Матрица после первого шага примет вид
3. Выполните второй шаг метода Гаусса, предполагая, что 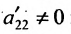
После второго шага матрица примет вид
4. Продолжая аналогичные преобразования, придёте к одному из двух случаев:
а) либо в ходе преобразований получим уравнение вида
тогда данная система несовместна;
б) либо придём к матрице вида:
где 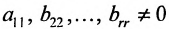
связано с тем, что в процессе преобразований матрицы исключаются строки, состоящие из нулей.
5. Использовав конечную матрицу, составьте систему, при этом возможны два случая:
Система имеет единственное,решение 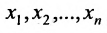
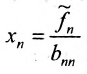
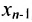
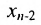
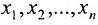
5.2. 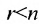
Тогда r неизвестных будут базисными, а остальные (n-r) — свободными. Из последнего уравнения выражаете неизвестное 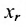
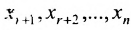
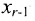
Система имеет в этом случае бесконечное множество решений.
Приведенный алгоритм можно несколько видоизменить и получить алгоритм полного исключения, состоящий в выполнении следующих шагов. На первом шаге:
- составляется расширенная матрица;
- выбирается разрешающий элемент расширенной матрицы
(если
, строки матрицы можно переставить так, чтобы выполнялось условие
);
- элементы разрешающей строки (строки, содержащей разрешающий элемент) оставляем без изменения; элементы разрешающего столбца (столбца, содержащего разрешающий элемент), кроме разрешающего элемента, заменяем нулями;
- все другие элементы вычисляем по правилу прямоугольника: преобразуемый элемент равен разности произведений элементов главной диагонали (главную диагональ образует разрешающий элемент и преобразуемый) и побочной диагонали (побочную диагональ образуют элементы, стоящие в разрешающей строке и разрешающем столбце):
— разрешающий элемент (см. схему).
Последующие шаги выполняем по правилам:
1) выбирается разрешающий элемент 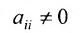
2) элементы разрешающей строки оставляем без изменения;
3) все элементы разрешающего столбца, кроме разрешающего элемента, заменяем нулями; • •
4) все другие элементы матрицы пересчитываем по правилу прямоугольника.
На последнем шаге делим элементы строк на диагональные элементы матрицы, записанные слева от вертикальной черты, и получаем решение системы.
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом
Из последней матрицы находим следующее решение системы
уравнении:
Ответ:
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом
Система привелась к ступенчатому виду (трапециевидной форме):
в которой неизвестные 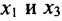
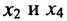
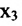
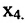
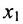
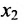
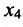
в котором 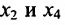
Если в общем решении положить 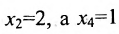
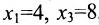
Ответ: система имеет бесконечное множество решений, общее решение которой записывается в виде:
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом 
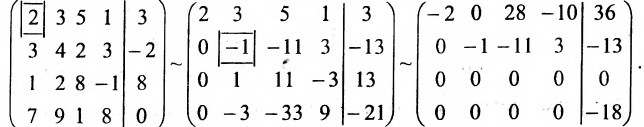
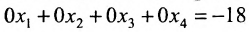
Ответ: система несовместна.
Замечание 1. Если дана система уравнений (6.1.1), в которой число уравнений m равно числу неизвестных n (m=n) и определитель этой системы 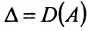
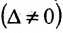
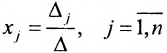
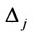
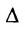
Если же такую систему (m-n) записать в матричной форме AX=F, то её решение можно найти по формуле 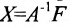
Замечание 2. Используя метод Гаусса, тем самым и алгоритм полного исключения, можно находить обратную матрицу. Для этого составляется расширенная матрица, в которой слева от вертикальной черты записана матрица А, а справа — единичная матрица. Реализовав алгоритм полного исключения, справа от вертикальной черты получаем обратную матрицу, а слева — единичную.
Пример:
Найти обратную матрицу для матрицы:
Решение:
то обратная матрица 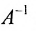
Покажем, что
ответ
Исследование совместности и определённости системы. Теорема Кронекера-Капелли
Рассмотрим систему (6.1.1) m линейных уравнений с n неизвестными при любых m и n (случай m=n не исключается). Вопрос о совместности системы решается следующим критерием.
Теорема 6.2.1. (критерий Кронкера-Капелли). Для того, чтобы система линейных уравнений(6.1.1) была совместна, необходимо и достаточно, чтобы ранг матрицы А системы был равен рангу расширенной матрицы 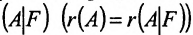
Доказательство и Необходимость:
Предположим, что система (6.1.1) совместна и 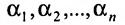
Из этих равенств следует, что последний столбец матрицы 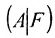
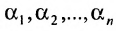
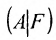
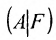
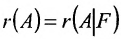
Достаточность. Пусть 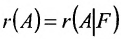
столбцов матрицы А, которые одновременно будут базисными столбцами и матрицы 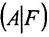
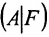
где 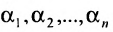
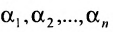
эта система совместна.
Совместная система линейных уравнений (6.1.1) может быть либо определенной, либо неопределенной.
Следующая теорема даст критерий определенности.
Теорема 6.2.2. Совместная система линейных уравнений имеет единственное решение тогда и только тогда, когда ранг матрицы А системы равен числу п ее неизвестных.
Таким образом, если число уравнений m системы (6.1.1) меньше числа ее неизвестных n и система совместна, то ранг матрицы системы 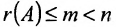
В случае 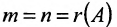
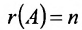
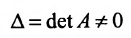
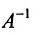
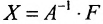
Следует отметить, что, решая систему (6.1.1) методом Гаусса, мы определяем и совместность, и определённость системы.
Пример:
Исследовать на совместность и определённость следующую систему линейных уравнений:
Решение:
Составим расширенную матрицу заданной системы. Определяя её ранг, находим тем самым и ранг матрицы системы. Для нахождения ранга матрицы применим алгоритм метода Гаусса.
Из последней матрицы следует, что ранг расширенной матрицы 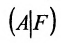
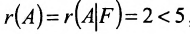
Однородные системы линейных уравнений
Система линейных уравнений (6.1.1) называется однородной, если все свободные члены 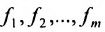
Эта система всегда совместна, так как очевидно, что она имеет нулевое решение
Для однородной системы важно установить, имеет ли она ненулевые решения. Этот факт устанавливается следующей теоремой.
Теорема 6.3.1. Для того, чтобы однородная система имела ненулевые решения, необходимо и достаточно, чтобы ранг г матрицы А системы был меньше числа неизвестных n (r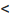
Доказательство. Необходимость. Пусть система (6.3.1) имеет ненулевое решение. Тогда она неопределённая, т.к. имеет еще и нулевое решение. В силу теоремы 6.2.2 ранг матрицы неопределённой системы не может равняться n потому что при r(А)=n система определённая. Следовательно, 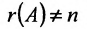
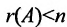
Достаточность. Если 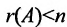
Следствие 1. Если число неизвестных в однородной системе больше числа уравнений, то однородная система имеет ненулевые решения.
Доказательство. Действительно, ранг матрицы системы (6.3.1) не может превышать m. Но так как по условию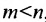
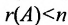
Следствие 2. Для того, чтобы однородная система с квадрат-ной матрицей имела ненулевые решения, необходимо и достаточно, чтобы её определитель 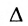
Доказательство. Рассмотрим однородную систему с квадратной матрицей:
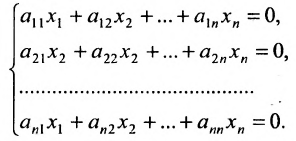
Если определитель матрицы системы 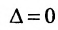
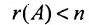
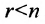
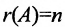
Пример:
Решить систему однородных линейных уравнений:
Решение:
Составим матицу системы и применим алгоритм полного исключения:
Из последней матрицы следует, что 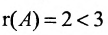
Используя последнюю матрицу, последовательно находим общее решение:
Неизвестные 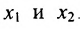
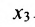
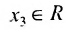
Фундаментальная система решений. Общее решение неоднородной системы линейных уравнений
Рассмотрим систему однородных линейных уравнений
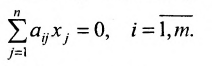
системы m линейных однородных уравнений с n неизвестными можно рассматривать как вектор-строку 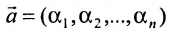
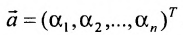
1) сумма двух решений также является решением системы, т.е.
если 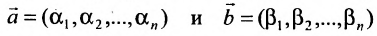
(6.4.1), то и 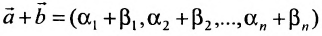
2) произведение решений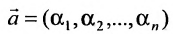
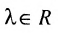
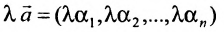
Из приведенных свойств следует, что
3) линейная комбинация решений системы (6.4.1) является решением этой системы.
В частности, если однородная система (6.4.1) имеет хотя бы одно ненулевое решение, то из него умножением на произвольные числа, можно получить бесконечное множество решений.
Определение 6.4.1. Фундаментальной системой решений для системы однородных линейных уравнений (6.4.1) называется линейно независимая система решений, через которую линейно выражается любое решение системы (6.4.1).
Заметим, что если ранг матрицы системы (6.4.1) равен числу неизвестных n (r(А)=n), то эта система не имеет фундаментальной системы решений, так как единственным решением будет нулевое решение, составляющее линейно зависимую систему. Существование и число фундаментальных решений определяется следующей теоремой.
Теорема 6.4.1. Если ранг матрицы однородной системы уравнений (6.4.1) меньше числа неизвестных (r(А)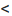
Сформулируем алгоритм построения фундаментальной системы решений:
- Выбираем любой определитель
порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули.
- Свободным неизвестным придаём поочерёдно значения, равные элементам первой, второй и т.д. строк определителя
, и каждый раз из общего решения находим соответствующие значения базисных неизвестных.
- Из полученных n-r решений составляют фундаментальную систему решений.
Меняя произвольно определитель 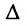
Пример:
Найти общее решение и фундаментальную систему решений для однородной системы уравнений:
Решение:
Составим матрицу системы и применим алгоритм полного исключения.
Для последней матрицы составляем систему:
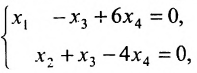
, из которой находим общее решение:
в котором 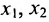
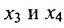
Построим фундаментальную систему решений. Для этого выбираем определитель 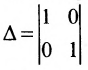
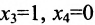
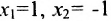
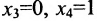
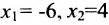
Таким образом, построенные два решения (1; -1; 1; 0) и (-6; 4; 0; 1) составляют фундаментальную систему решений.
Если ранг матрицы системы однородных линейных уравнений (6.4.1) на единицу меньше числа неизвестных: 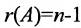
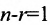
Рассмотрим теперь неоднородную систему m линейных уравнений с n неизвестными (6.1.1). Если в системе (6.1.1) положить 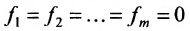
Решения системы (6.1.1) и её приведенной системы удовлетворяют свойствам:
- Сумма и разность любого решения системы (6.1.1) и любого решения её приведенной системы является решением неоднородной системы.
- Все решения неоднородной системы можно получить, прибавляя к одному (любому) её решению поочерёдно все решения её приведенной системы.
Из этих свойств следует теорема.
Теорема 6.4.2. Общее решение неоднородной системы (6.1.1.) определяется суммой любого частного решения этой системы и общего решения её приведенной системы.
Пример:
Найти общее решение системы:
Решение:
Составим расширенную матрицу (A|F) заданной системы и применим алгоритм полного исключения:
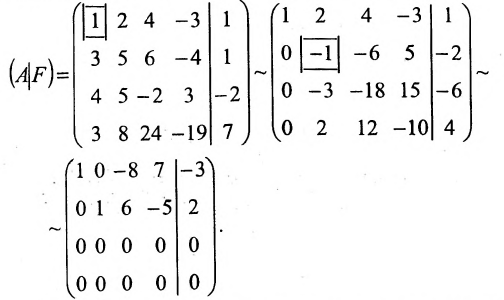
Преобразованной матрице соответствует система уравнений:
из которой находим общее решение системы:
, где 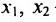
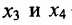
Покажем, что это общее решение определяется суммой любого частного решения заданной системы и общего решения приведенной системы.
Подставляя вместо свободных неизвестных 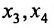
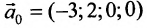
Очевидно, что общее решение приведенной системы имеет вид:
Суммируя частное решение заданной системы и общее решение приведенной системы, получим общее решение (6.4.2) исходной системы.
Отметим, что общее решение системы (6.1.1) можно представить в векторном виде:
где 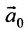
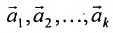
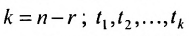
Формула (6.4.4) называется общим решением системы (6.1.1) в векторной форме.
Запишем общее решение системы примера 6.4.1 в векторной форме. Для этого определим фундаментальную систему решений приведенной системы. Возьмём определитель 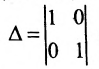
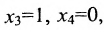
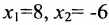
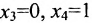
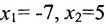
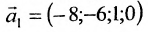
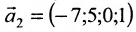
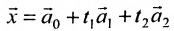
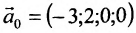
Видео:Совместные и несовместные системы уравненийСкачать

Определение метода Гаусса
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
Пример:
Решить систему уравнений методом Гаусса:
Решение:
Выпишем расширенную матрицу данной системы 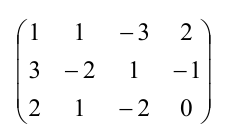
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
б) третью строку умножим на (-5) и прибавим к ней вторую:
В результате всех этих преобразований данная система приводится к треугольному виду:
Из последнего уравнения находим 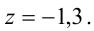
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Вычисление метода Гаусса
Этот метод основан на следующей теореме.
Теорема:
Элементарные преобразования не изменяют ранга матрицы.
К элементарным преобразованиям матрицы относят:
- перестановку двух параллельных рядов;
- умножение какого-нибудь ряда на число, отличное от нуля;
- прибавление к какому-либо ряду матрицы другого, параллельного ему ряда, умноженного на произвольное число.
Путем элементарных преобразований исходную матрицу можно привести к трапециевидной форме
где все диагональные элементы 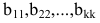
Пример:
Найти ранг матрицы
1) методом окаймляющих миноров;
2 ) методом Гаусса.
Указать один из базисных миноров.
Решение:
1. Найдем ранг матрицы методом окаймляющих миноров. Выберем минор второго порядка, отличный от нуля. Например,
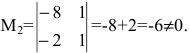
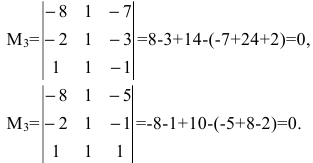
2. Найдем ранг матрицы методом Гаусса. Производя последовательно элементарные преобразования, получим:
- переставили первую и третью строки;
- первую строку умножили на 2 и прибавили ко второй, первую строку умножили на 8 и прибавили к третьей;
- вторую строку умножили на -3 и прибавили к третьей.
Последняя матрица имеет трапециевидную форму и ее ранг равен двум. Следовательно, ранг исходной матрицы также равен двум.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Производная функции одной переменной
- Дифференциальные уравнения с примерами
- Обратная матрица — определение и нахождение
- Ранг матрицы — определение и вычисление
- Определители второго и третьего порядков и их свойства
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🔍 Видео
Решение систем уравнений методом подстановкиСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Математика без Ху!ни. Метод Гаусса.Скачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Матричный метод решения систем уравненийСкачать

Свойства систем линейных уравнений (01)Скачать

9 класс, 10 урок, Основные понятия, связанные с системами уравнений и неравенств с двумя переменнымиСкачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

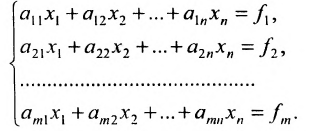
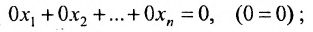
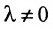 ;
;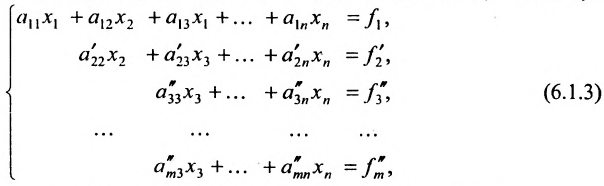
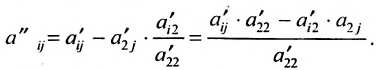
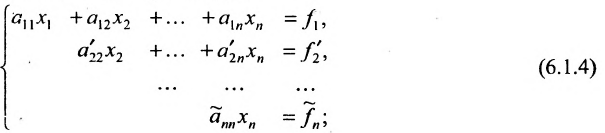
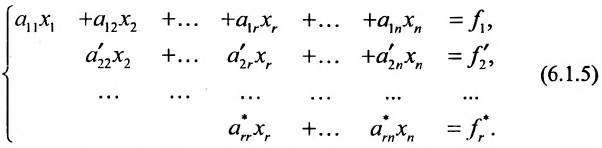

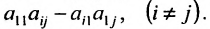
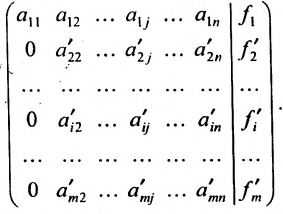
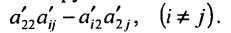

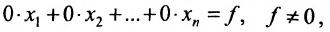
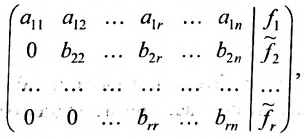
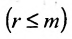
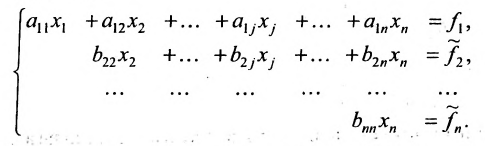
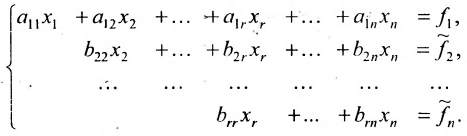
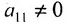 (если
(если 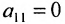 , строки матрицы можно переставить так, чтобы выполнялось условие
, строки матрицы можно переставить так, чтобы выполнялось условие 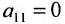 );
);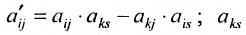 — разрешающий элемент (см. схему).
— разрешающий элемент (см. схему).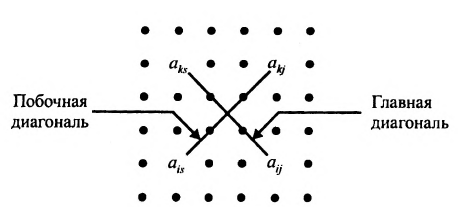
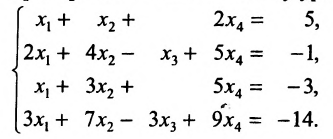


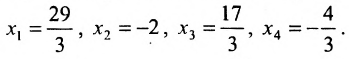
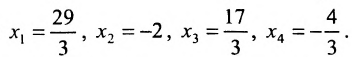
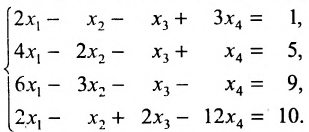

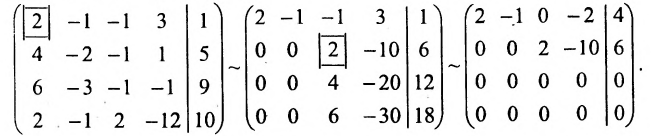

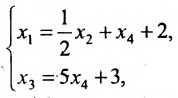
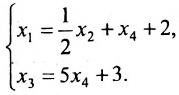
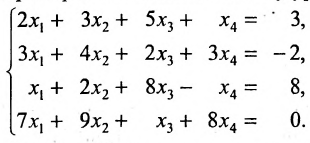
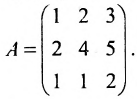
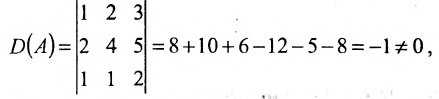

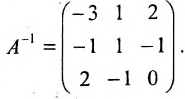
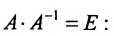
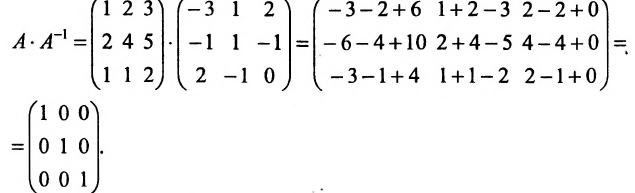
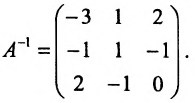
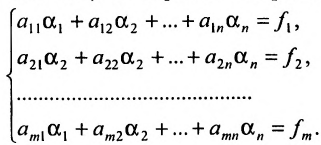
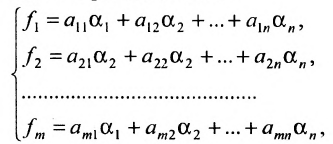
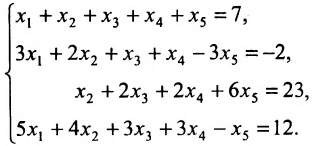

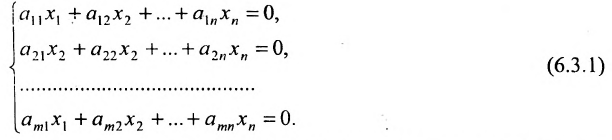
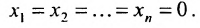
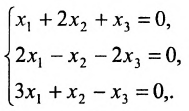
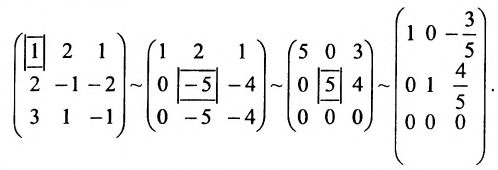
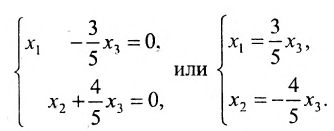
 порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули.
порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули. , и каждый раз из общего решения находим соответствующие значения базисных неизвестных.
, и каждый раз из общего решения находим соответствующие значения базисных неизвестных.