Понятие уравнения 6 класс петерсон

Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Урок по математике 6 класс «Понятие уравнения»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Сценарии уроков по учебнику «Математика, 6 класс», часть 3

Тема: « Понятие уравнения ».

1) сформировать понятие уравнения, корня уравнения, множества решений уравнения;

2) повторить и закрепить: действия с рациональными числами, понятие противоположного и обратного числа, высказывания и их отрицания, решение уравнений методом весов, методом проб и ошибок.

1) задание для актуализации знаний:

= 2,4; ; = 4,2

;

;

;

;

.

; ; ; .

= 21; ; ; ; .

2. Корень уравнения.

3. «Решить уравнение».

2) План урока

Уравнение — равенство, содержащее переменную.

Корень уравнения: число, при котором равенство будет верным.

Решить уравнение – найти все его корни или доказать, что корней нет.

4) образец выполнения задания в парах

№ 71 (г) 2х 2 + 5х + 2 = 0

Если х = — , то 2 × (- ) 2 + 5 × (- ) + 2 = 0;

2 × — + 2 = 0;

— + 2 = 0;

а) в правой части число увеличено на 4, а в левой части число уменьшено на 3, левая часть всегда больше правой.

г) нет такого рационального числа, квадрат которого был бы равен 2

5) эталон для самопроверки самостоятельной работы

Если x = –2, то 2 × (–2) 2 + 5 × (–2) + 2 = 0; Корень уравнения: число, при котором равенство будет верным.

0 = 0 (И), – 2 корень уравнения.

Ответ: – 2 корень уравнения.

½ 2x – 3 ½ = –1 Решить уравнение – найти все его корни или доказать, что корней нет.

Модуль не может быть отрицательным числом, уравнение не имеет корней.

Ответ: корней нет.

2 y + 3( y – 2) – 5( y – 3) = 0; Решить уравнение – найти все его корни или доказать, что корней нет.

2 y + 3 y – 6 – 5 y + 15 = 0;

При умножении 0 на любое число получится 0, уравнение не имеет корней.

Ответ: корней нет.

1. Самоопределение к деятельности.

Цель этапа: 1) включить учащихся в учебную деятельность;

2) определить содержательные рамки урок: продолжить работать с уравнениями.

Организация учебного процесса на этапе 1:

— Здравствуйте, ребята! Что мы изучали на прошлых уроках? (Как приводить подобные слагаемые.)

– Где используется приведение подобных слагаемых? (При упрощении выражений, при решении уравнений.)

– Сегодня на уроке мы с вами продолжим работать с понятием, с которым вы встретились первый раз еще в начальной школе.

2. Актуализация знаний и фиксация затруднения в деятельности.

Цель этапа: 1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: решение простейших уравнений;

2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;

3) зафиксировать все повторяемые понятия и алгоритмы в виде схем и символов;

4) зафиксировать индивидуальное затруднение в деятельности, демонстрирующее на личностно значимом уровне недостаточность имеющихся знаний: понятие уравнения.

Организация учебного процесса на этапе 2:

1. Укажите , если = 2,4; , если = 4,2

– Можно ли утверждать, что результаты получатся одинаковые в каждом случае?

2. Найдите х из равенства:

; ; ; ; .

– Назовите полученные результаты в порядке убывания:

3. Не решая, найдите уравнения с положительным корнем и уравнения с отрицательным корнем.

; (–)

; (–)

; (+)

. (–)

– Подчеркните записи, которые являются уравнениями:

= 21; ; ; ; .

3. Выявление причин затруднений и постановка цели деятельности.

Цель этапа: 1) организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности;

2) согласовать цель и тему урока.

Организация учебного процесса на этапе 3:

— Какова же цель нашего урока? (Мы будем работать с уравнениями.)

— Сформулируйте тему урока. (Уравнение.)

— Верно. Сегодня на уроке мы с вами вспомним определение понятию «уравнение», вспомним, что такое «корень уравнения», узнаем ,что значит «решить уравнение». Запишите тему урока в тетрадь: «Уравнение».

На доске появляется план урока:

2. Корень уравнения.

3. «Решить уравнение».

4. Построение проекта выхода из затруднения.

Цель этапа: 1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;

2) зафиксировать новый способ действия в знаковой, вербальной форме и с помощью эталона.

Организация учебного процесса на этапе 4:

— Посмотрите внимательно на равенства:

= 21;

— Вы назвали эти равенства уравнениями. Почему? (В этих равенствах есть переменная.)

— Дайте определение понятию уравнение. (Учащиеся высказывают свои мнения, затем на доске появляется определение понятию «уравнение».)

Уравнение — равенство, содержащее переменную.

– Что такое корень уравнения? (Это число, при подстановке, которого получится верное равенство.)

Корень уравнения: число, при котором равенство будет верным.

– Что значит решить уравнение? (Найти его корень.)

– Угадайте корень первого уравнения. (Учащиеся предлагают свои варианты, каждый вариант обсуждается.)

– Сколько решений получилось? (Два корня.)

– Если мы найдём только один корень, можно считать, что мы решили уравнение? (Нет, т.к. есть ещё число, при котором равенство будет истинным.)

– Угадайте корни второго уравнения. (Учащиеся предлагают свои варианты, каждый вариант обсуждается.)

– Сколько нашли корней? (Три корня.)

– Что значит решить уравнение? (Найти все корни уравнения.)

– Может ли уравнение не иметь корней? Придумайте такое уравнение. (Учащиеся приводят свои примеры.)

– Уточните, что, значит, решить уравнение? (Учащиеся проговаривают свои варианты.)

Решить уравнение – найти все его корни или доказать, что корней нет.

5. Первичное закрепление во внешней речи.

Цель этапа: зафиксировать изученное учебное содержание во внешней речи.

Организация учебного процесса на этапе 5:

Устно № 69 (а, б, в — фронтально; г, д — в парах, объясняя друг другу)

а) не является уравнением; б) уравнение; в) не является уравнением;

г) не является уравнением; д) уравнение.

Если х = 2, то 2 × (2 ) + 5 × 2 + 2 = 0.

20 = 0 (Л), число 2 не является корнем уравнения.

№ 71 (г) – в парах с проверкой по образцу.

№ 74 (б) – фронтально

Первое слагаемое в левой части неотрицательное число, второе слагаемое положительное число, значит сумма положительная.

№ 74 (а, г) – в парах с проверкой по образцу.

Упростим левую часть уравнения:

х любое рациональное число.

Ответ: х любое число из множества Q .

№ 75 (в) – в парах с проверкой по образцу.

6. Самостоятельная работа с самопроверкой по эталону.

Цель этапа: проверить своё умение применять новое учебное содержание в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки.

Организация учебного процесса на этапе 6:

№ 71 (б); № 74 (в); № 75 (б)

После выполнения работы учащиеся проверяют работу по эталону, ставя знаки » + » или «?». Анализируются ошибки.

7. Включение в систему знаний и повторение.

Цель этапа: 1) тренировать навыки использования нового содержания совместно с ранее изученным: решение уравнений на разных множествах чисел;

2) повторить учебное содержание, которое потребуется на следующих уроках: составление уравнения и решения его методом «весов», методом проб и ошибок, методом перебора.

Организация учебного процесса на этапе 7:

— Когда произведение трех множителей равно 0? (Когда хотя бы один из них равен 0.)

— Сколько уравнений можно составить? (Три.)

3х = 0; или х + 2 = 0; или 3х + 5 = 0;

х = 0 : 3; х = 0 — 2; 3х = 0 – 5;

x = –1

Ответ: а) <-2; –1 ; 0 >; б) ; в) Æ ; г) Æ ; д)

а) (х – 4) × 2 + 9 = х – 2; б) (х + 3) : 3х = 11 : 15;

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Математика 6 класс Учебник Дорофеев Петерсон часть 3

8 => а > 9, б)а>9 => а>8. (^а)х = 2 => = 32, б)х^ = 32 => х = 2. В последних двух примерах мы не указали множество значений переменной. В таких случаях предполагается, что переменная принимает значения из множества всех уже известных нам чисел, то есть из множества рациональных чисел. Таким образом, мы видим, что знак следования => соединяет два предложения с переменными и образует новое высказывание общего вида: из первого предложения следует второе. Первое предложение назовем условием, а второе — заключением, или следствием, первого. Запись вида P-=>Q будем называть логическим следованием. Эту запись можно читать так: «Если Р, то Q», или так: «Из Р следует Q*, «Q есть следствие Р». Иногда вместо слова «следует» говорят более образно — «вытекает», и тогда знак => показывает «направление течения»: из первого предложения « вытекает » второе. Ош Сформулируй предложения, используя глагол «следует»: а) если животное млекопитающее, то оно кормит детей молоком; б) если вода превратилась в лед, то ее температура меньше или равна нулю. 232| Прочитай предложения и назови условие и заключение. Что ты замечаешь? а) Если натуральное число оканчивается на О, то оно кратно 5. б) Если число кратно 5, то оно оканчивается на 0. в) Если сумма цифр натурального числа делится на 3, то и само число делится на 3. г) Если число делится на 3, то и сумма его цифр делится на 3. д) Если каждое слагаемое делится на некоторое число, то их сумма тоже делится на это число. е) Если сумма чисел делится на некоторое число, то и каждое слагаемое делится на это число. 233| Прочитай высказывания и определи, истинны они или ложны. В каких высказываниях условие и заключение поменялись местами? а) п кратно 8 => л кратно 4; в)а > Ь => Ь п кратно 8; г) а Ь>а. 51 Глава 3, § 5, п.1 23^ Сформулируй высказывания с использованием союза «если. то. * и запиши их на математическом языке. а) Число, противоположное отрицательному, положительно. б) Произведение правильных дробей является правильной дробью. в) Параллельные прямые не пересекаются. г) Вертикальные углы равны. ш Придумай предложение, являющееся логическим следованием, и запиши его на математическом языке. 236| Вычисли устно и продолжи ряд ответов на одно число, сохраняя закономерность: -7 :0,1 + 40 •0,09 -1,6 -12 • 10 +270 :(-30) + 1,6 -3 :(-4) + 0,15 •(-2) -0,7 2,8 + 5,2 : 0,2 -50 + 8,4 -2,4 •0,5 + 4 (-0,1) :0,4 237| Пусть А — множество чисел, кратных 5, В — множество чисел, кратных 10, С — множество чисел, кратных 3, и D — множество чисел, кратных 9. На диаграмме Эйлера-Венна точками обозначены элементы множеств А, В, С и В, являющиеся трехзначными числами. Придай возможные значения переменным а, Ь, с, d, е, fvi g. 238| Найди истинные высказывания и составь из соответствующих им букв имя древнегреческого философа, которого считают основоположником науки логики: 815 кратно 3; 0 815 делится на 5; 1536 не делится на 9; рп] 1536 не кратно 4; 0 52 704 делится на 2 и на 9; [е] 52 704 кратно 18; [н] 14 625 не кратно 3 или 25; 75 является делителем 14 625; 712 • 15 + 340 не кратно 5; [

ь] 10 800 -63-47 делится на 9; 325 • 120 • 79 кратно 10; 325 • 120 • 79 не делится на 200; 0 9 является делителем 438^; 1 и| 405^ делится на 25 и на 81; 0 246’^ кратно 8; 210^ — 60^ не делится на 100. 52 Глава 3, § 5, п.2 239| Упрости выражение, найди его коэффициент и буквенную часть: а) 5а-(-1,8&); б) -4п • (-0,7×1/); в) -Зт ‘ —к’ 1,5т; О д)-|аЬ-1,85-(-2,5а^); г) |-с • (-l,6d) • (-0,5с); е) 2х • • l,3xz^ О На дискотеке девочек было на 6 больше, чем мальчиков. Если число девочек увеличить на 100% , а число мальчиков увеличить на 150%, то девочек и мальчиков станет поровну. Сколько девочек и сколько мальчиков было на дискотеке? Найди значения выражений; а) -з(|/г + I) + 5(1,2/г — 0,8), если ^ |; б) а(4а — 0,95) — 6(1,6а — 36) — 1,5(а^ + 26^), если а = -0,6; 6 = -2,6 24^ Запиши высказывание на математР1ческом языке с помощью знака =>, подчеркни условие одной чертой, а заключение — двумя. Найди ложные высказывания. Как их опровергнуть? а) Произведение двух отрицательных чисел положительно. б) Сумма двух правильных дробей является правильной дробью. в) Разность двух целых чисел является целым числом. г) Частное двух рациональных чисел — число рациональное. На мороженое Аня истратила имевшихся у нее денег, а на блокнот — 15 11 остатка. Сколько денег у нее осталось после этого, если за блокнот она заплатила 6 рублей? Увеличь число на 40%: (б,829 + • 0,7 — (б,629 — ^ • 2,з)) — (-0,3)^ • 1б| — 1,25 : (-^) + 6 : з|| + 5,684 : (-1,4) [24^ Запиши в десятичной системе счисления числа: lOlOlOl^, 1212g, 3210^, 4040g, 20406^, 1234,2, 500^^. 2. Отрицание следования. Итак, из того, что где-то идет дождь, следует, что земля в этом месте и в это время мокрая. С другой стороны, каждому понятно, что если земля мокрая, то отсюда вовсе не следует, что в это время и в этом месте идет дождь: вполне может оказаться, что землю здесь специально полили. 53 Глава 3, § 5, п.2 Другими словами, для обоснования высказывания «Из того, что земля мокрая, не следует, что идет дождь» мы приводим пример ситуации, когда условие «земля мокрая* истинно, а заключение «идет дождь» ложно. Это верно и для математических предложений. Например, из того, что п делится на 5, не следует, что п оканчивается цифрой 5. Ведь число 10 делится на 5, но не оканчивается на 5. Мы видим, что для обоснования предложения со словами «не следует» достаточно привести пример, когда условие истинно, а заключение ложно. Это и понятно: мы уже говорили, что предложение со словом «следует* является общим высказыванием, а чтобы доказать, что общее высказывание ложно, достаточно привести хотя бы один контрпример. Еще раз подчеркнем, что для этого контрпримера условие должно быть истинным, а заключение ложным. Среди примеров, рассмотренных в предыдущем пункте, имеются как истинные, так и ложные высказывания: 1а 16 2а 26 За 36 4а 46 И Л И Л Л и И И Для ложных высказываний приведем контрпримеры. № Ложное высказывание Контрпример 16 Если натуральное число делится на 3, то оно делится на 9, или п делится на 3 л делится на 9. Число 3: 3 делится на 3 (условие истинно), но не делится на 9 (заключение ложно). 26 Если дробь неправильная, то обратная к пей дробь правильная, или — > 1 ^ 8 => х>9. Число 8,5: 8,5 больше 8 (условие истинно), но меньше 9 (заключение ложно). Итак, отрицанием следования Р =>Q является предложение (Р Q), или P^Q, которое читается ^Неверно, что из Р следует Q* или «Из Р не следует Q*. Для его обоснования достаточно привести пример, когда Р истинно, а Q ложно. 54 —________-_____________________________________ Глава 3, § 5, п.2 24^ Переформулируй предложения, используя глагол «следует». Построй отрицания: а) Если светит солнце, то вода в реке тецлая. б) Человек, знающий нотную грамоту, умеет играть на скрипке. в) Стрелки часов совмещаются в полдень. г) Любая неправильная дробь больше единицы. д) Все углы четырехугольника прямые. е) Если площади фигур равны, то равны и сами фигуры. 247| Переведи высказывания с математического языка на русский. Найди ложные высказывания и построй их отрицания. Обоснуй свой ответ. а) => X = у; д)п>5=>п>6(пеN); б) => т = п im,n^N); е)х>5 => х^б; ж) т gN, п ^ N => т — п ^ N; г) I X I = I//1 => X = £/; 3)x^eQ => xeQ. 248| а) Назови тему и рему высказываний. Что общего в высказываниях и чем они отличаются? 1. Квадрат является прямоугольником. 2. Прямоугольник является квадратом. в) х^ = у’^ X I = у => х = у. б) Сформулируй данные высказывания с помощью глагола «следует». Что ты замечаешь? в) Найди ложное высказывание и построй его отрицание. 2491 Запиши высказывания на математическом языке с помощью знака =>. Найди ложные высказывания, построй отрицания и обоснуй их истинность. а) Если первое число меньше второго, а второе — меньше третьего, то первое число меньше третьего. б) Если первое число на 5 меньше второго, а второе — на 5 меньше третьего, то первое число на 5 меньше третьего. в) Если первое число кратно второму, а второе — кратно третьему, то первое число кратно третьему. г) Если первое число в 2 раза больше второго, а второе — в 2 раза больше третьего, то первое число в 2 раза больше третьего. Что ты замечаешь? [250| Запиши в общем виде правила деления суммы, разности и произведения на число. Пользуясь этими правилами, вычисли устно: а) (15-86) : 43; в) 6986 : 7 + 14 : 7; д) (15 • 19 + 38): 19; б) (9494-5): 94; г) 5564 : 52 — 364 : 52; е) (3500 — 48 • 70): 35. 55 Глава 3, § 5, п.2 251| Восстанови цепочки вычислений и расшифруй логические термины. Что они означают? 252| Найди множество корней уравнения: а) ЦЗх — 7) — 2<х — 15) = 5 — 3(2х + 9); б) JC — 3ех его измерений равна 5,8 дм. Найди объем и площадь боковой поверхности этого параллелепипеда. Ф |257| Запиши числа 9, 25, 32, 75, 100 в системе счисления с основанием d = 2. 56 Глава 3, § 5, п.З 3. Обратное утверждение. Легко заметить, что в каждом примере пункта 1 предложения (а) и (б) похожи друг на друга. Именно, если предложение (а) имеет вид Р =>Q, то предложение (б) имеет вид Q=> Р: условие одного предложения является заключением другого, и наоборот. Определение. Предложение «Если Q, то Р» (Q к предложению «Если Р, то Q* (Р => Q). Р) называется обратным Таким образом, чтобы получить предложение, обратное к предложению с союзом «если. то. *, надо просто поменять в нем местами условие и заключение. Отсюда и употребление слова «обратное*: в обратном предложении условие и заключение идут в обратном порядке. При этом исходное предложение Р Q являет- ся обратным к своему обратному Q => Р. Поэтому утверждения Р => Q и Q => Р называются взаимно обратными. Если предложение явно сформулировано как условное с союзом «если. то. », то переход к обратному предложению не сложен. Но обратные предложения существуют для любых высказываний общего вида, а не только для условных предложений. В этом случае для построения предложения, обратного к данному, можно данное высказывание переформулировать с союзом «если. то. *. Например, мы говорим: «Все кощачьи — четвероногие», но в точности ту же мысль выражает условное предложение: «Если животное принадлежит семейству кошачьих, то оно является четвероногим*. Конечно, так не говорят, поскольку первое предложение короче и понятней. Но для второго предложения легче сформулировать обратное: «Если животное является четвероногим, то оно принадлежит семейству кошачьих*. А это предложение означает, что « все четвероногие принадлежат семейству кошачьих*. Другими словами, предложения «Все кошачьи — четвероногие» и «Все четвероногие принадлежат семейству кошачьих* являются взаимно обратными. При этом ни то, ни другое предложение по форме не является условным. Различать взаимно обратные предложения необходимо и в языке, и в математике — хотя бы потому, что из истинности данного утверждения не следует, что истинно обратное утверждение, — оно может быть как истинным, так и ложным. Путаница в этом вопросе может привести в повседневной жизни к недоразумениям, а в математике — к ошибкам. 57 Глава 3, § 5, п.З На практике для формулировки обратного предложения к общему высказыванию обычно не делают тех шагов, которые мы прошли в рассмотренном выше примере. Все обстоит гораздо проще, если вспомнить понятия темы и ремы. Именно, в предложении «Все кошачьи — четвероногие» мы говорим о кошачьих <тема) и утверждаем, что они четвероногие <рема). В предложении «Все четвероногие принадлежат семейству кошачьих» мы говорим о четвероногих <тема) и угверждаем, что они -кошачьи НОК (а, Ь) = аЬ’, г) а II ft => ft II а; д) jct/ = О => дг = О или I/ = О; е) х^- х^- Запиши высказывания на математическом языке. Докажи, что обратные к ним высказывания ложны, и построй их отрицания. а) Если число меньше или равно 5, то оно меньше 6. б) Если число кратно 40, то оно кратно 4 и 10. в) Если числа равны, то равны и квадраты этих чисел. г) Если числа равны, то равны и модули этих чисел. д) Две параллельные прямые лежат в одной плоскости. е) Две перпендикулярные прямые имеют общую точку. Для данных общих высказываний построй обратные высказывания. Найди ложные высказывания, построй их отрицания и обоснуй истинность построенных отрицаний. а) Любое натуральное число больше или равно 1. б) Все числа, кратные 10, оканчиваются на 0. в) Треугольник является многоугольником. г) Квадрат является прямоугольником. д) Сумма противоположных чисел равна 0. е) Произведение взаимно обратных чисел равно 1. Придумай общее высказывание и построй для него обратное. Найди взаимно обратные высказывания. С помощью каких союзов можно объединить их в одно предложение? а) = &^ => I а I = I ft |; в) | а | = | ft | => б) => а = Ь; г) а = Ь => = ft®. 59 Глава 3, § 5, п.З 2^ Придумай высказывание с союзом «если. то. »> и построй для него обратное. Как объединить эти два высказывания в одно предложение? 2651 Вычисли и запиши следующее число в ряду ответов, сохраняя закономерность: б) -0,8-0,7 1 а) 0,24 : (-0,04) -30-(-0,16) в) -1 : (-9) 1,4 — 5 -4+4,2 — • “’9 0,56 : (-0,2) -^•2 ■ 2 — — 0,5 18 ’ 1,2 : 2,7 2661 1) Увеличь число д:: а)наЗ; б) в 4 раза; в) на треть; г) на 160%. 2) Уменьши число t/: а) на 2; б) в 5 раз; в) на четверть; г) на 30%. 2^ Найди; а) — от 0,35; б) 0,08 от 12; в) 25% от 5,6; г) 70% от а; д) число, ^ которого равны 1,8; е) число, 0,9 которого равны 72; ж) число, 2% которого равны 0,64; з) число, 40% которого равны Ь. Блицтурнир. Составь выражения и упрости их: а) Груши дороже яблок на 15 р., а яблоки дешевле винограда в 2 раза. На сколько груши дешевле винограда, если яблоки стоят а р.? б) Первый букет цветов стоит Ь р., второй — на 40% дороже первого, а стоимость третьего составляет треть общей стоимости первого и второго букетов вместе. Сколько рублей надо заплатить за все три букета? в) От куска ткани длиной d м отрезали в первый раз 20% всей длины, во второй раз — 30% всей первоначальной длины, а в третий раз — на 5 м меньше, чем во второй раз. Сколько метров ткани осталось в куске? г) В бидоне было х л молока. Сначала из него отлили 25% всего молока, а потом 20% остатка. Сколько молока еще осталось в бидоне? 269| 1) Разложи числа на простые множители и найди их наибольший общий делитель и наименьщее общее кратное: а) 18 и 21; 6)28 и 245; в) 16 и 160; г)27 и 100. 2) Чем интересны примеры (в) и (г)? Закончи предложения: Если число а является делителем числа Ь, то НОД (а,Ь) = НОК (а,Ь) = „ Если число а кратно числу h, то НОД (а,Ь) = . НОК (а.Ъ) = . 60 Значение выражения 4 + ^ + о у ___________________Глава 3, § 5, п.З 5 ^ 8 ^ 11 — + — + — принадлежит множеству Iz 15 18 , /29 39 39 59 99 ,, „

это значит найти такое число с, которое при умножении на Ь дает а*, «Чтобы установить мировой рекорд, необходимо и достаточно показать результат лучше действующего мирового рекорда» и т.д. фш 2831 Прочитай высказывания разными способами: а) IJC1 0); б) i I > а х > а или х 0); в) Число а на 7 меньше, чем число Ь о а = Ь — 7; г) Число п кратно 9 о Сумма цифр числа п кратна 9. 284| Запиши высказывания на математическом языке и прочитай два следования, которые объединены в каждом предложении. а) Число хв2 раза больше, чем число у, тогда и только тогда, когда х = 2у. б) Для того чтобы число а было кратно 3, необходимо и достаточно, чтобы сумма цифр числа а была кратна 3. в) Вычесть из числа а число Ь — это значит найти такое число с, которое при сложении с Ь дает а. г) Квадрат числа х равен 9 в том и только в том случае, когда л: = 3 или х = -3. 63 Глава 3, § 5, п.4 285| Докажи с помощью контрпримера, что следующие утверждения не являются равносильными: а) х^ = 25 и х = 5; в) | дг! = 7 и д: = 7; б) = 16 и х = -4; г) |дг| ad = о а о а а 6 «d а . а с T

d о а + Ь [287J Придумай два равносильных высказывания и объедини их в одно предложение тремя разными способами. 288| Запиши решение уравнений, используя знак : а)-0,5дс + 3 = 0; в)-дс — Зд: + 2д: = 0,4; д) -2дс: — 4 + дг = -0,8; 1 О е) 0,6х — д: -Ь 2,5 = 1 • б) -0,5д: -I- 3 • д: = -5; г) 0,02д: — д: + 0,7х = -2,8; |289| Найди неизвестные члены пропорции. Расположи полученные числа в порядке возрастания, сопоставив их соответствующим буквам, и расшифруй слово. Что оно означает? Г8 = | = = ¥ 32=i. rpnA = ii2 = rpi 14 ДС 1,6 д: lU X 0,5 ^16-2 Ш _5 q,1 H 10 у Отметь на координатной прямой цветным карандашом множество точек, удовлетворяющее данному неравенству. Запиши множество его целых решений и 2 дробных решения: а)-2 х = . или х = . ; б) laf| = 2 X = . или х = . ; в) |л:| 1 о д: > . или X X- хвойное, покрытосеменное (х е D, где D — множество деревьев); а делится на 6 => 3 с: а = Ьс (а,Ь.с ^ N). Таким образом, предложения, выражающие общие свойства предметов, можно представить в виде логического следования. Обратное к логическому следованию предложение тоже является следованием и может быть истинным или ложным. Так, утверждение, обратное первому предложению, ложно, поскольку сосна тоже является деревом хвойным и покрытосеменным. А вот предложение, обратное второму, истинно по определению делимости. Каждое понятие обладает множеством свойств. Эти свойства, как мы видели, могут быть представлены в виде следований. Например, квадрат обладает следующими свойствами: ABCD — квадрат => zA = = / С =/ D = 90″ ABCD — квадрат => АВ — ВС = CD = DA ABCD — квадрат => ABCD — прямоугольник, АВ = ВС = CD = DA Из трех утверждений, обратных данным утверждениям, истинным является только последнее. Значит, можно записать: ABCD — квадрат ABCD — прямоугольник, АВ = ВС = CD = DA Свойства, однозначно определяющие объект, называют его характеристическими свойствами, или признаками. Другими словами, признаки понятия равносильны самому понятию. Для того чтобы дать определение некоторого понятия, необходимо использовать только его характеристические свойства. Например, мы не можем использовать в качестве определения квадрата первые два свойства -контрпримеры приведены на рисунках 18 и 19: В Рис. 18 Рис. 20 Вместе с тем равенство всех сторон прямоугольника характерно только для квадрата, а значит, является его признаком (рис. 20). Поэтому квадрат можно определить как «прямоугольник, все стороны которого равны». 3* 67 Глава 3, § 5, п.5 В определении понятий над знаком иногда ставят латинские буквы def (от латинского definitio — определение). Таким образом, определение квадрата на математическом языке можно записать так: def ABCD — квадрат ^ABCD — прямоугольник, АВ = ВС — CD = DA 299| На какие классы разбивают данное множество объектов следующие свойства: а) «2 не тонет в воде» (г е С, где С — множество металлов); б) «к имеет парламент» (к е D, где D — множество государств); в) «л кратно 9» (л е N); г) *1 л: I е iV» (аг е Z); д) + 1 = о» (j/е Q); е) «а II6» (а, Ь ^ Р, где Р — множество прямых и ц Ь — фиксированная прямая из этого множества). 3001 Какие свойства описывают следующие предложения? Какие из этих свойств являются признаками? а) л кратно 9 => сумма цифр числа л кратна 9 (л б) а : Ь = с => с • Ь = а (а, Ь, с & Q, Ь Ф 0); в) ABCD — прямоугольник => /Л — прямой; г) а||6 => а П 6 = 0 (а, 6 е Р, где Р — множество прямых). Запиши, используя знак def, определение: а) умножения рациональных чисел; б) правильной дроби; в) прямоугольника; г) трапеции. му. 3021 Выполни действия: . 3 5 ^>14 7 ’ ^ 6 15 ’ 303| Реши уравнения: а) (d — 6) — : Если число кратно 2 и 3, то оно кратно 6. Объедини оба высказывания в одно предложение разными способами. Два пешехода идут с разной скоростью: 50 м/мин и 70 м/мин. Сейчас расстояние между ними равно 600 м. Каким оно станет через t мин, если пешеходы движутся: а) навстречу друг другу; б) в противоположных направлениях; в) вдогонку; г) с отставанием? Запиши для всех четырех случаев формулу зависимости расстояния d м между ними от времени движения t мин. (Встречи за это время не произойдет.) Найди число, 20% которого составляют: 15,7 — 14,7 : (-0,75 + 0,7 : (-2-|)) • 2,45. Уменьши на 20% число: Ш -0,02 • (6,2 : 0,31 — ^ • 7,2) -1,52 _________________р__________ ^•(-2,2): (-0,1)-10 3221 Реши уравнение методом проб и ошибок’. х(х -Ь 4) = 45, х ^ N. 3231 Реши уравнение методом перебора’, — 8л: = 20, х ^ N. 70 Глава 4 гэометрия § 1. Геометрические фигуры на плоскости 1. Что такое геометрия? Рисунки и определения геометрических понятий. Слово геометрия греческого происхождения, и нетрудно догадаться, как оно переводится на русский язык. Гея — богиня земли в древнегреческой мифологии, metrio — по-гречески «мерить». Поэтому геометрия -это, можно сказать, землемерие. Само название геометрии показывает, что она возникла непосредственно из практических потребностей, главным образом связанных с измерением земельных участков. При решении этих задач нужно было измерять площади, а значит, в первую очередь, измерять отрезки. Таким образом, геометрия исторически связана с измерениями. Но это лишь ее «детство», и впоследствии содержание геометрии значительно расширилось — до такой степени, что измерения отошли в ней на дальний план, а в центре внимания оказались геометрические фигуры и их свойства. Ранее мы уже познакомились со многими геометрическими фигурами. Каждый без труда может изобразить на плоскости точку, прямую, луч, отрезок, прямоугольник и квадрат, различные углы, окружность, параллельные и перпендикулярные прямые и т.д. Однако даже таким уже хорошо знакомым понятиям в математике необходимо дать определения, так как в определениях описываются характеристические свойства фигур, и, значит, только на их основе можно проводить математические рассуждения. Например, невозможно судить об истинности высказывания *Острый угол меньше тупого угла*, не зная определений этих углов. Многие определения нам уже встречались, но вспомнить их гораздо труднее, чем изобразить нужную геометрическую фигуру на бумаге. Например, легче нарисовать отрезок (рис. 21), чем дать его определение: «Отрезок — это часть прямой, ограниченная двумя точками». Точно так же изобразить окружность, угол, прямоугольник гораздо легче, чем увидеть и выразить в речи их существенные свойства. 71 Глявэ 4, 5 1, п. 1 В каждом определении есть новое — то, что определяется, и уже известное («старое») — то, с помощью чего определяется новое. Например, в определении «Квадратом называется прямоугольник с равными сторонами» понятие «квадрат* — новое, а уже известное — «прямоугольник с равными сторонами*. Но если вдуматься глубже, осознать новое можно, только понимая «старое», — в данном случае понятия прямоугольник, сторона прямоугольника и равные стороны. Другими словами, определение нового понятия всегда опирается на другие понятия, которые, в свою очередь, нуждаются в определениях. Но эти определения также должны опираться на ранее определенные понятия: например, понятие «прямоугольник» опирается на «прямой угол», «прямой угол», то есть угол в 90°, — на «градус* и т.д. Таким образом, складывается, казалось бы, безвыходное положение — получается бесконечный процесс. В математике выход был найден в III веке до нашей эры: древнегреческий математик Евклид осознал, что всем геометрическим понятиям определения дать невозможно и поэтому некоторые из них должны быть введены без определения. Такие понятия называют основными. Ясно, что в качестве основных целесообразно ввести только те понятия, которые легко воспринимаются с помощью рисунка или материального образа. К основным понятиям в геометрии относятся, прежде всего, точка, прямая и плоскость. Наглядное представление о точке дает след, который оставляет на бумаге неподвижный остро заточенный карандаш, представление о прямой — туго натянутая тонкая нить, представление о плоскости — спокойная гладь воды. Чтобы от рисунка перейти к определению какого-либо понятия, нужно выявить его характеристические свойства. Например, чтобы дать определение окружности, можно вспомнить, что при построении ее с помощью циркуля расстояние между концами ножек циркуля не меняется. Поэтому окружность можно определить как множество всех точек плоскости, находящихся на одинаковом расстоянии от одной заданной точки (рис. 22). Это определение окружности опирается на понятия «множество», «точка», «расстояние», «одинаковый », « плоскость *. D 72 Глава 4, § 1, n. 1 Для определения смежных углов (рис. 23) надо заметить, что одна сторона у них общая. Но этого недостаточно, так как у углов на рис. 24 тоже есть общая сторона, но они не являются смежными. Поэтому надо отметить еще одну существенную особенность смежных углов — две другие их стороны образуют прямую. ‘с В Значит, смежные углы — это два угла, одна сторона у которых общая, а две другие образуют прямую. Это определение смежных углов опирается на понятия ♦ прямая*, «угол*, «сторонаугла*, «общаясторона*. Заметим, что определение смежных углов можно дать и по-другому: смежными называются два угла, одна сторона у которых общая, а две другие являются дополнительными лучами. Эти два определения равносильны: из второго следует первое, и наоборот. Однако второе определение опирается уже на несколько другие геометрические понятия — «угол*, «сторонаугла*, «общаясторона* и «дополнительные лучи*. До сих пор мы шли от рисунка к определению. Обратный путь — от определения к рисунку — часто оказывается более простым. Для этого надо лишь хорошо знать предыдущие понятия — те, на которые новое понятие опирается. Например, по определению: В Хордой окружности называется отрезок, соединяющий две точки этой окружности легко сделать рисунок хорды: достаточно отметить на окружности любые две точки и соединить их отрезком (рис. 25). В математике очень полезно, давая определение некоторого понятия, проиллюстрировать его рисунком. Действительно, геометрический образ, в отличие от текстовых определений, часто легче воспринимается и лучше запоминается. Очень полезны рисунки и при решении математических задач, где успех решения часто напрямую зависит от точности рисунка, иллюстрирующего задачу. 73 Глава 4, § 1, п. 1—————————————————- Татьяна и Петр дали следующие определения квадрата. • Татьяна: «Квадратом называется четырехугольник с равными сторонами». • Петр: «Квадратом называется параллелограмм, все углы которого прямые*. Почему нельзя согласиться с такими вариантами определения? Предложи свой вариант и сравни его с вариантом, данным в тексте учебника. В Л/» 325 — 329 по определениям сделай рисунка, назови определяемые понятия и понятия, на которые они опираются. Построй логическую последовательность введения этих определений и установи, в каких случаях ее можно изменить, а в каких — нет. а) Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. б) Треугольником называется фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами. в) Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника. г) Отрезком называется часть прямой, ограниченная двумя точками. Эти точки принадлежат отрезку и называются его концами. а) Два луча с общим началом, составляющие прямую, называются дополнительными лучами. б) Лучом называется часть прямой, ограниченная только одной точкой. Эта точка принадлежит лучу и называется его началом. в) Два угла называются вертикальными, если стороны одного из них являются дополнительными лучами для сторон другого. г) Углом называется геометрическая фигура, образованная двумя лучами с общим началом. Лучи называются сторонами угла, а их общее начало -вершиной угла. а) Треугольник называется прямоугольным, если один его угол прямой. б) Косинусом острого угла прямоугольного треугольника называется отношение длины прилежащего катета к длине гипотенузы. в) Прямым углом называется угол, величина которого равна 90″. г) В прямоугольном треугольнике сторона, противолежащая прямому углу, называется гипотенузой, а две другие стороны называются катетами. 74 Глава 4, § 1, п.1 а) Отрезок, соединяющий точку окружности с ее центром, называется радиусом окружности. б) Окружностью называется фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки. Эта точка называется центром окружности. в) Хорда, проходящая через центр окружности, называется диаметром. г) Хордой окружности называется отрезок, соединяющий две ее точки. а) Ромб — это параллелограмм, у которого все стороны равны. б) Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются. в) Параллелограмм — это четырехугольник, у которого противолежащие стороны попарно параллельны. г) Прямоугольник — это параллелограмм, у которого все углы прямые. Сформулируй определение квадрата, основываясь на понятии: а) прямоугольник; б) ромб; в) параллелограмм. Прочитай определение биссектрисы, угла. Биссектрисой угла называется луч, который исходит из вершины угла и делит часть плоскости, ограниченную углом, на две равные части. Пользуясь им, предложи свой вариант определения биссектрисы угла треугольника. Сделай рисунки биссектрисы угла и биссектрисы угла треугольника. Как ты считаешь, какой из нарисованных углов называют центральным! Почему? Проверь по справочнику. Нарисуй несколько центральных углов окружности и сформулируй определение этого понятия. Какую из прямых па рисунке можно назвать касательной к окружности, а какую — секущей! Почему? Предложи свои варианты определений касательной и секущей и сделай рисунки. Сравни свои определения с определениями этих понятий в справочнике. 75 Глава 4, § 1, п.1 3341 Что общего у окружности и круга и чем они отличаются друг от друга? Предложи свой вариант определения круга, пользуясь понятиями «окружность», «плоскость». Изобрази круг и окружность с помощью циркуля и цветных карандашей. 335| Исходя из значения слова «дуга» в обыденной речи, найди рисунок, на котором цветом изображена дуга окружности. Предложи свой вариант определения дуги окружности и сделай рисунок. |336| На рисунках изображены секторы круга. Выяви существенные свойства сектора и предложи свой вариант его определения. Сделай свой рисунок сектора. 1) 2) ^ 3) @1^ ззд Что означает запись: ^ ? Изобрази с помощью геометрических фигур ч 3 —ч 5 ч 7 ч числа: а) — ; б) — ; в)- ; г) 2— . 3381 Сравни дроби, если значения всех переменных — натуральные числа: а) А„ б) | и 7 11’ ч 3 9 I “ 5’ д)зА и 2^^; ^ 19 19 ж) -п п + 1 8 . 15’ ч 4 12 7 “ 25’ е) 0,6 и А; 16 з) -у з: -1-1 и . У |339| Выполни действия, сопоставь ответам соответствующие буквы и расшифруй слово. Что оно означает? О 1 1 М ^ 3 Т 4 -3 + 2т Я 6 18 2 3 И 22 55 1 11 F, 5 2|-1^ Г 3 4 8 12 6 15 -1А — II 14 21 ^80 ^60 -Is 1,3 1 12 -0,9 1,3 -0,2 2 9 -2 — 6 76 Глава 4, § 1, п.1 3401 Реши уравнения: . X X ^ X _ ^^9 3 18 б) J/ В М 341 3 4 6 ’ 342 реши задачи разными способами. .5 2^1 а) Длина окружности переднего колеса повозки равна 2,8 м, а заднего — 3,5 м. Какое расстояние проехала повозка, если переднее колесо сделало на 50 оборотов больше заднего? б) Длина окружности заднего колеса кареты на 0,8 м больше длины окружности переднего колеса. Какое расстояние проехала карета, если заднее колесо сделало 450 оборотов, а переднее — на 75 оборотов больше? 342| а) Печник должен был сложить печь за 12 дней. Но он выкладывал в день на 0,25 больше, чем предполагал, и поэтому закончил работу на 4 дня раньше намеченного срока. Чему равен объем печи, если печник работал равномерно? б) Бригада рабочих должна была сделать ремонт дороги за определенный срок, ремонтируя в день 2 км. Однако в день она ремонтировала на 0,1 км больше, и поэтому за 3 дня до срока ей осталось отремонтировать 4,5 км. Сколько километров дороги бригада уже отремонтировала? Прочитай определения, найди определяемые понятия и укажи понятия, на которые они опираются. Сделай рисунки, соблюдая логическую последовательность введения определений. а) Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны. б) Замкнутая ломаная линия без самопересечений, все точки которой принадлежат одной плоскости, называется многоугольником. в) Многоугольник, имеющий четыре вершины (стороны), называется четырехугольником . г) Прямоугольником называется параллелограмм, у которого все углы прямые. 344| На рисунках изображены сегменты круга. Выяви существенные свойства сегмента и предложи свой вариант его определения. Сделай рисунок. 77 Глава 4, § 1, п.2 3451 Выполни действия, сопоставь ответам соответствующие буквы и расшифруй математические термины. Найди в тексте учебника и запиши в тетрадь их определения. Е 4 7 МЛ Jmx . 3 « 1 — + — 9 18 5 3 ‘-т 2 . А 9 р 21 7 5 2 У 9 ^ , 1 X —— 4 11 , 1 О 8 3 к -*-5 Н -1—3 д ^11 ®11 -1^ -2^ 15 6 35 ^14 -4,1 5 6 2 3 1 24 -4,1 -1,2 -3-^ ^11 -4,1 -lA 11 0,9 -1 ш Реши уравнения: ^ ^ _ о, ^26 б) — — 2 = — • 3 5 ’ . 2 , — 32 . Найди число, 24% которого составляют: (-2f 0,58-0.42-2|)-l|:(-2f)- О Реши задачу разными способами: Автобус проходит расстояние от города до озера за 3 часа. Автомобиль, скорость которого на 12 км/ч больше скорости автобуса, проходит это же расстояние на 30 мин быстрее. Чему равно расстояние от города до озера? Сколько диагоналей можно провести в четырехугольнике? А в треугольнике, пятиугольнике, шестиугольнике, л-угольнике? Сколько возникает на окружности дуг, если на ней поставлены две точки? А если точек 3, 4, 10, л? 2. Классификация геометрических фигур. Свойства геометрических фигур в силу их большого практического значения интересовали людей еще в глубокой древности. Однако многие свойства даже таких простейших фигур на плоскости, как треугольник, были найдены не сразу, а в результате длительной и кропотливой работы с конкретными треугольниками, а затем обобщения полученных выводов. Может быть, это имел в виду великий Евклид, когда говорил древнеегипетскому царю Птолемею I, что царских путей в геометрии нет. 78 _______________________________________________________Глава 4, § 1, п.2 Рассмотрим, например, треугольник АВС (рис. 26). В Заметим, что все углы треугольника АВС острые. Можем ли мы на этом основании сделать вывод, что углы всех треугольников острые? Конечно, нет. Уже имеющийся опыт работы с треугольниками убеждает нас в том, что это не так: углы треугольников могут быть и прямыми, и тупыми, при этом сумма всех углов треугольника всегда равна 180°. Поэтому треугольники по виду углов можно разбить на три класса: остроугольные — все углы которых острые, прямоугольные имеющие один прямой угол, и тупоугольные — имеющие один тупой угол: остроугольный Рис. 27 Эти классы интересны тем, что любой треугольник попадает ровно в один класс, и тем самым множество Т треугольников определенным образом упорядочивается. На рис. 27 показана диаграмма Эйлера-Венна множества Г, где Т^, и обозначают соответственно множества остроугольных, прямоугольных и тупоугольных треугольников. Разбиение множества на классы, при котором каждый элемент попадает ровно в один класс, называется классификацией. Полученные таким образом классы являются непересекающимися, и их объединение составляет все множество. Свойство, в соответствии с которым множество разбивается на классы, называют основанием классификации (в нашем примере — «вид углов*). Иногда в классах геометрических фигур выделяются подклассы, то есть подмножества. Например, в множестве треугольников Т можно выделить треугольники, которые имеют две равные стороны, — их называют равнобедренными; в множестве равнобедренных треугольников, в свою очередь, можно выделить равносторонние — те, у которых равны все три стороны. равнобедренный равносторонний Все равносторонние треугольники являются равнобедренными — ведь они удовлетворяют определению равнобедренных треугольников. Обозначая их соответственно Т и Т , можно записать Т е Т определение углов каждого вида. На какие понятия опираются эти определения? б) На какие классы можно разбить все углы а, где 0“ . На какие понятия опирается это определение? б) Является ли равнобедренный треугольник равносторонним? А наоборот? Нарисуй диаграмму Эйлера-Венна, иллюстрирующую взаимосвязь между множеством всех треугольников, множеством равнобедренных и множеством равносторонних треугольников. Определи на глаз, какие из треугольников, изображенных на рисунке, являются: а) остроугольными; б) прямоугольными; в) тупоугольными; г) равнобедренными; д) равносторонними? Есть ли треугольники, которые обладают сразу несколькими из перечисленных свойств? а) Может ли быть треугольник равнобедренным и тупоугольным? А равнобедренным и прямоугольным? Сделай рисунки. б) Нарисуй в тетради диаграмму Эйлера-Венна, показывающую классификацию треугольников по виду углов. Покажи, как располагаются на ней подмножества равнобедренных и равносторонних треугольников. Какие сочетания видов треугольников возможны? а) Начерти равнобедренный треугольник АВС (АВ — ВС) и измерь транспортиром углы при основании АС. Что ты замечаешь? Сформулируй гипотезу. б) Начерти равнобедренный треугольник АВС (АВ = ВС) и проведи медиану к его основанию АС. Что ты замечаешь? Сформулируй гипотезу. Как ты считаешь, на какие виды треугольников можно распростронить построенные гипотезы? Обоснуй свой ответ. 81 Глава 4, § n.2 358| а) Построй отрезок АВ, равный 5 см. Затем проведи две дуги радиусом 4 см и центрами в точках А и В до их пересечения в точке С. Соедини точки А, В и С отрезками и определи вид треугольника АВС. Измерь с помощью транспортира углы получившегося треугольника. Что ты замечаешь? Сформулируй гипотезу. На какие виды треугольников ее можно распространить? Сколько общих точек могут иметь прямая и окружность? Рассмотри все возможные случаи и сделай рисунки. Является ли это разбиение классификацией? Прямая называется касательной к окружности, если она имеет с этой окружностью одну общую точку. Начерти прямую, касательную к окружности, и проведи радиус в точку касания. Что ты замечаешь? Сформулируй гипотезу. Можно ли распростронить ее на секущие к окружности? Почему? фш 3611 Какие из окружностей на рисунке являются вписанными в треугольник, а какие — описанными около него? Выяви существенные признаки вписанной и описанной окружностей и предложи свой вариант определений этих понятий. 362| Расположи ответы примеров в порядке возрастания, сопоставь им соответствующие буквы и расшифруй общенаучное понятие. Что оно означает? 5 3 3 4 7 ■ 15 Т ^■Н1) п Г О _9.16 45 А -|(-з,б) и -5:0,6 Е 11 (-4) 363| Прочитай предложения. Определениями каких понятий они могут служить? Почему? Поясни их с помощью диаграммы Эйлера-Венна и проиллюстрируй примерами из разных областей знания: 1) AczB о (аеА ^ а ^ В)-, 2) д:еАПБохеАид:еВ; 3) дгеАиВ о хеА или х е В. Прочитай высказывания и проиллюстрируй их с помощью диаграммы Эйлера-Венна. Найди ложные высказывания, построй отрицания и обоснуй их истинность. 1) АсВиВсС А а С; 3) дгеАиАсВ => х ^ В; 2) АаС VI В czC => А а В; 4) х х е А. 82 Глава 4, § 1, n.2 [365| Как найти часть от числа? Как найти число по его части? Найди: а) — от 16,2; б) 15% от 3,04; в) — от а; д) число, — которого равны 1,5; 5 е) число, 6% которого составляют 4,2; ч 2 ж) число, — которого составляют х; г) 58% от Ь; з) число, 140% которого равны у. [366| Найди часть, которую одно число составляет от другого, и вырази ее процентах: а) 18 от 50; б) 9 от 72; в) 1,2 от 15; г) от 5-; д) 0,42 от 5,6; е) 11^ от 7,2; 5 ж) а от Ь; з) т от п. |367| Блицтурнир. а) Посадили d семян. Из них k семян проросли. Чему равен процент всхожести семян? б) Цена товара на складе равна а р. Торговая наценка в магазине равна 24%. Сколько стоит этот товар в магазине? в) Акции фирмы в январе стоили п р., что составило 80”/) их стоимости в феврале. Сколько стоили акции этой фирмы в феврале? г) За месяц построено 60% дороги. Чему равна длина всей дороги, если осталось построить с км? д) Бак автомобиля вмещает х л бензина. На каждые 100 км пути расходуется 20% объема бака. Сколько литров бензина потребуется на 350 км пути? е) Фермер с каждого гектара из 4 га своего поля собрал по 6 т картофеля. На семена он оставил 25% всего урожая, а остальной картофель отвез на рынок. Сколько тонн картофеля он отвез на рынок? |36^ В городской думе 80 депутатов, среди которых 4 независимых депутата, а остальные представляют интересы трех партий. Число депутатов от первой партии на 20% больше, чем от второй, а число депутатов от второй партии составляет 62,5% числа депутатов третьей. а) Сколько депутатов от каждой из трех партий представлено в городской думе? б) Может ли какая-либо партийная фракция заблокировать принятие решения, для которого требуется квалифицированное большинство голосов 2 (не менее —) всех депутатов думы? О 83 Глава 4, § 1, п.2 3691 1) На бумаге в клетку отмечены шесть точек (рис. 29). Выпиши все треугольники, вершины которых могут быть в этих точках. 2) Подчеркни разными цветами треугольники, которые являются: а) остроугольными; б) прямоугольными; в) тупоугольными; г) равнобедренными. Переведи с математического языка на русский определение касательной к окружности; А В С D К м Рис. 29 Прямая а — касательная к окружности (О; г) в точке А (iff а П (О; г) = . Сколько касательных к окружности можно провести из точки, лежащей вне окружности? А из точки, лежащей на окружности? Сделай рисунки и сформулируй гипотезу. Можем ли мы считать ее верной для всех окружностей на основании выполненных построений и измерений? Учеников шестых классов попросили высказать свое мнение об утверждении: «Чтобы хорошо учиться по математике, надо заучивать текст учебника». Распределение их мнений приведено на круговой диаграмме. Сколько шестиклассников высказали то или иное мнение, если всего в опросе приняли участие 160 человек? А что по этому поводу думаешь ты? «Затрудняюсь ответить» 7,5% В трех школах поселка 1260 учеников. Число учащихся первой школы на 10% меньше, чем второй, а число учащихся второй школы составляет 80% от числа учащихся третьей школы. Сколько учащихся в каждой из этих трех школ? Расположи ответы примеров в порядке убывания, сопоставь им соответствующие буквы и расшифруй название геометрической фигуры. Начерти эту фигуру и придумай ее определение; 0(-1Г |Т]-1,9 + 2| Я = (-3) ц И if-(-1,4) Т -if-(-4) Е 4-1 ^ (-1) 84 Глава 4, § 1, п.З 374| Найди процентное отношение чисел: 1)А и В; 2) В и А. Ф [37^ Дан прямоугольник, длины сторон которого относятся как 2:1. Разрежь его на части так, чтобы из них можно было составить: а) равнобедренный прямоугольный треугольник; б) равнобедренный тупоугольный треугольник; в) равнобедренный остроугольный треугольник. 3761 Сколько равносторонних треугольников ты видишь на рисунке? 3. Задачи на построение. Исследование свойств фигур с помощью измерений имеет существенный недостаток — эта процедура приводит всегда к приближенному результату. Основой измерительных приборов — например, линейки и транспортира — является шкала. На собственном опыте вы убедились, что при проведении измерений второй конец отрезка или вторая сторона угла чаще всего проходит между делениями шкалы (рис. 30). И даже если можно определить, какое деление ближе, результат нельзя считать точным. Такова неустранимая погрешность непосредственных измерений. Стремясь к большей точности, древние математики предпочитали строить геометрические фигуры, избегая сложных измерений, а используя лишь проведение прямых по линейке и проведение окружностей циркулем. Не будем отступать от традиций и мы. Но, поставив цель — точность построений, — надо всегда помнить о технике построений. Математические линии не имеют толщины, и поэтому практические построения тем точнее, чем лучше отточен карандаш и грифель циркуля. 85 Глава 4, § 1, п.З—————————————————— ! Итак, у нас есть линейка без делений и циркуль. Какие же базовые опера-I ции можно выполнять с помощью этих инструментов? Их всего пять: построе-i ние прямой (1), окружности (2), построение точки пересечения двух прямых i (3), прямой и окружности (4) и двух окружностей (5): ® / о л л Этих базовых операций оказывается достаточно для выполнения самых разнообразных построений. Древние греки даже считали, что с помощью циркуля и линейки без делений можно выполнить любое построение на плоскости, пока не столкнулись с некоторыми задачами, которые никто не мог решить на протяжении почти 24 веков. Лишь в XIX веке было установлено, что с помощью циркуля и линейки эти построения выполнить невозможно. Прочитать об этом можно в энциклопедической литературе, а мы сейчас убедимся в удивительных возможностях двух простых инструментов — циркуля и линейки. Рассмотрим несколько задач. Описание их решения приведено как на обычном языке, так и на языке множеств — пусть каждый использует тот язык, который ему удобен. Дополнительно введем новые обозначения, которые помогут различать в записи прямую, луч, отрезок и окружность: (АВ) — прямая АВ; [АВ) — луч АВ; [АБ] — отрезок АВ; (О, г) — окружность с центром О и радиусом г. Слова типа «отложим», «проведем» и т.д. в описании на математическом языке будем опускать. «Равными» фигурами мы, как и прежде, будем считать фигуры, которые можно совместить наложением (при этом фигуры разрешается переворачивать в пространстве). Задача!. Построение отрезка, равного данному. Построение: Построить: [CD] такой, что CD = АВ. D 1) а. Се а; 2) г = АБ, (С; г); 3) П е а П (С; г). [CD] — искомый. Проведем произвольную прямую а и отметим на ней точку С. Возьмем раствор циркуля, равный данному отрезку, и проведем окружность с центром в точке С. Одну из точек пересечения этой окружности с прямой а обозначим D. Длина полученного отрезка CD равна радиусу проведенной окружности, то есть АВ. Следовательно, CD = АВ. Задача решена. Мы видим, что при проведении различных построений естественным образом возникает вопрос: как доказать их правильность? В данной задаче мы использовали для этого определение окружности. 86 Глава 4, § 1, п.З Для более сложных случаев необходимо использование общих свойств фигур, которые мы еще не изучали. Поэтому в настоящий момент мы можем лишь с некоторой степенью точности проверить правильность каждого конкретного построения с помощью, например, кальки или измерительных приборов. Строгие доказательства правильности рассмотренных построений разбираются в курсе геометрии старших классов. Построение отрезка, равного данному, выстроилось из основных операций 1, 2 и 4. Если данное построение нам встретится в следующих задачах, то мы не будем его повторять, а будем считать, что мы его уже провели. Таким образом, каждая рещенная задача будет расширять спектр наших возможностей. 3 а д а ч а 2. Построение треугольника, равного данному. Дано: Построение: В. 1) а; 2) [Л,С,] ^АВ 2) (А; г) Л (В; г) = ; 3) (СВ); 4) (СВ) Л [АВ] = . Точка М — искомая. Построим две пересекающиеся окружности одного радиуса г (где г > АВ) с центрами в концах данного отрезка АВ. Через точки С и В пересечения окружностей проведем прямую СВ. Точка пересечения прямой СВ с данным отрезком и есть искомая середина отрезка АВ. Задача решена. Заметим, что прямая СВ не только проходит через середину отрезка АВ, но и перпендикулярна к нему. Такую прямую называют серединным перпендикуляром к отрезку. Поэтому проведенное построение одновременно является и построением серединного перпендикуляра. 3 а д а ч а 6. Построение прямой, перпендикулярной данной и проходящей через данную точку. Рассмотрим два случая — когда данная точка принадлежит прямой и когда она прямой не принадлежит. I. Дано: Построение: Прямая а. ‘ В е а. Построить: прямую Ь такую, что В еЬ; Ь ±а. 1) (В; г) Л а = ; 2) Ы. CD, СВ = BD. Прямая Ь — искомая. 88 Глава 4j § 1, п.З 2. Дано: Прямая а. В ^ а. Построение: 4 1) (В; г) П а = ; 2) 61 СВ, CM = MD. Прямая Ь — искомая. Л Построить: прямую Ь такую, что В еЬ; Ь 1а. В обоих случаях проведем сначала окружность с центром в точке В, пересекающую прямую а в двух точках. Пусть это точки С и В. Затем построим серединный перпендикуляр Ь к отрезку СВ. Он пройдет через точку В. Прямая Ь — искомая. Задача решена. Для решения задач на построение далее нам потребуются следующие обозначения: угол и противолежащую сторону в треугольнике будем обозначать одной и той же буквой, причем угол обозначают прописной буквой, а сторону -строчной. Например, в треугольнике АВС: В а — сторона, противолежащая ZA; Ь — сторона, противолежащая /.В; с — сторона, противолежащая Z.C. ——-ь———-«с ^|37^ По описанию построения фигур, данному в тексте учебника, построй: а) отрезок, равный данному (задача 1); б) треугольник, равный данному (задача 2); в) угол, равный данному (задача 3); г) биссектрису данного угла (задача 4); д) середину данного отрезка (задача 5); е) прямую, перпендикулярную данной и проходящую через данную точку (задача 6). |37^ Построй треугольник АВС по трем сторонам а, 6 и с и определи вид этого треугольника: 1) 2) Сколько можно построить различных (не равных между собой) треугольников с тремя данными сторонами? Всегда ли эта задача имеет решение? Можно ли построить треугольник, у которого периметр равен 24 см, а сумма длин двух сторон — 9 см? 89 Глава 4, § 1, п.З Построй треугольник АВС по стороне h и прилежащему к ней углу А. Является ли решение однозначным? Всегда ли оно возможно? Какие виды треугольников могут получиться? 1) 2) Построй треугольник АВС по стороне h и двум прилежащим к ней углам А и С. Сколько различных треугольников можно построить по этим данным? Определяется ли треугольник этими элементами единственным образом? 1) 2) АС АС [38^ Построй треугольник АВС по двум сторонам а и 6 и углу А, прилежащему к стороне Ь. Является ли решение однозначным? 1) а 2) а |38j Построй треугольник АБС по двум сторонам а и с и углу В, заключенному между ними. Однозначно ли определяется треугольник этими элементами? 1) а 2) а В 384| Проанализируй решение задач № 378-383 и сформулируй гипотезу: из равенства каких элементов двух треугольников следует равенство самих треугольников? Как можно назвать эти свойства равенства треугольников? Можно ли считать твою гипотезу верной для любых треугольников? Почему? 90 Глава 4, § 1, п.З О Построй биссектрисы углов А, В иС треугольника АВС, если треугольник АВС: а) остроугольный; б) прямоугольный; в) тупоугольный. Что ты замечаешь? Сформулируй гипотезу. Построй серединные перпендикуляры к сторонам а, Ьис треугольника ASC, если треугольник АВС: а) остроугольный; б) прямоугольный; в) тупоугольный. Что ты замечаешь? Сформулируй гипотезу. Построй медианы сторон а, Ьис треугольника АБС, если треугольник АВС: а) остроугольный; б) прямоугольный; в) тупоугольный. Что ты замечаешь? Сформулируй гипотезу. Построй высоты треугольника АВС, проведенные к сторонам а, Ьис, если треугольник АВС: а) остроугольный; б) прямоугольный; в) тупоугольный. Что ты замечаешь? Сформулируй гипотезу. [389| Вычисли, сопоставь ответам соответствующие буквы и расшифруй названия знаменитых геометрических задач древности: а) Щ-2 + 0,6 [^0,1-0,08 [^-0,8-0,4 , [Т]о>3-3,1 К -0,15 + 0,2 [р] 0,54 — 5,4 -0,5-0,06 |

а|-1,32- 7,68 -0,56 -1.4 -9 0,02 -4,86 -9 0,05 -1.2 -4,86 -9 -0,56 -4,86 -1,2 -2,8 -9 б) Щ -0,8 • (-3) рЙ] -0,42 • 5 [т] (-0,8)^ -6,4: (-4) Щ 0,24-(-10) |

у| 2,1 : (-10) -8:0,2 Щ-4 *(-0,01) |

’ДорофМ1, 6 кл. Ч. 3 97 Глава 4, § 1, п.4 Если мы измерим длины получившихся отрезков медиан, то сможем проверить еще одно свойство: точка пересечения медиан делит их в отношении 2:1, считая от вершины. Это свойство медиан треугольника можно сформулировать так: Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2 : 1, считая от вершины. Мы познакомились с четырьмя замечательными точками треугольника. Но свойства этих точек далеко не исчерпывают всех свойств треугольника. Приведем лишь некоторые открытия великого математика Леонарда Эйлера (1707- 1783 гг.). Он доказал, что центр описанной окружности треугольника АВС совпадает с точкой пересечения окружностей, описанных около треугольников ABjCj, AjBCj и А^В^С, где А^, В, и Cj — середины сторон АС, СВ и АВ (рис. 40). Рис. 41 А вот еще одно открытие Эйлера: окружность, проходящая через середины сторон треугольника, пройдет и через основания его высот (рис. 41). Удивительным является и то, что некоторые из четырех замечательных точек связаны определенными соотношениями. Например, точка пересечения медиан М, ортоцентр Я и центр описанной окружности О лежат на одной прямой, причем точка М делит отрезок ОН в отношении 1 : 2 (рис. 42). ОёШ Построй окружность, описанную около треугольника АВС, если треугольник АВС: а)остроугольный; б) прямоугольный; в)тупоугольный. Построй окружность, вписанную в треугольник АВС, если треугольник АВС: а) остроугольный; б) прямоугольный; в) тупоугольный. Построй ортоцентр треугольника АВС, если треугольник АВС: а) остроугольный; б) прямоугольный; в) тупоугольный. ш Практическая работа. Точка пересечения медиан является одновременно центром тяжести треугольника. Чтобы познакомиться с этим свойством, начерти на плотном листе картона произвольный треугольник АВС и найди точку О пересечения его медиан. Затем вырежь треугольник АВС, расположи его горизонтально и помести на вертикальный стержень (например, на острие карандаша или ручки) сначала в точке О, а потом в других точках. Что ты наблюдаешь? ш |4Ш 98 Глава 4, § 1, п.4 1^ [420| Сравни дроби: а) 3,6 и 3,600; в) 0,207 и 0,21; д) 1,76 и 1,756; б) 0,4 и 0,09; г) 5,03 и 4,98; е) 0,0938 и 0,1. Прочитай число: 0,2803951476. Зачеркни пять цифр так, чтобы получилось: а) возможно большее число; б) возможно меньшее число. Расположи числа в порядке возрастания, сопоставь их соответствующим буквам и расшифруй имя великого ученого-геометра античности: 0,51; 0,05; 0,1; 0,508; 0,058; 0,008; 0,8; 0,5; И И о л н 0 й] 0 0,015. 0 д) -2,002-2,9; е) -4,06 • (-20,5); ж) -0,7752 : (-1,9); з) 218,08 : (-7,25). Выполни действия: а) -0,286- 18,4; б) 17,9-20,205; в) -5,98 + 48,004; г) -3,08-4,192; Закончи предложение: «Несократимую дробь можно записать в виде конечной десятичной дроби в том и только том случае, когда ее знаменатель не имеет простых делителей, кроме . » Найди дроби, которые можно перевести в десятичные, и выполни перевод: 17 9 5 12 10 24 а) б) 2^-5’ 2-5=*’ 3-22’ 22-3’ 7-52’ 3-2^-52’ i. 1. i. J.. JL. 3 4 ’ 5’ 6’ 60’ 25’ 8′ Реши примеры по столбцам и предложи правило, по которому можно было бы записать следующее число в ряду ответов: а) 4.2-1 б) 1 : 1,2 в)1д-3 _1. к 2 ■ 28 1,3-(-2^) Докажи, что данную дробь нельзя перевести в конечную десятичную, и запиши ее в виде бесконечной периодической дроби, указав период: 6-з| 9,6 :2| l|-0,75 а)|: 6)i; в) 12 ’ , 6 ,35 , 23 ,47 ,25 ^>-6’ ‘>18 • Образец: II — 1,5333. — 1,5(3); II = 0,407407. — 0,(407). 4* 99 Глава 4, § 1, п.4 Й281 Замени данную обыкновенную дробь десятичной с точностью до целых, десятых, сотых, тысячных: а)^- 77. 26’ 96 , 127 ®) —; г) 49 ’31 4291 Автомобиль проехал расстояние от А до В со скоростью Oj км/ч за часов, а обратный путь от В до А — за часов. Запиши с помощью буквенного выражения, чему равны: а) расстояние от А до В; б) скорость движения от В до А; в) общее время движения туда и обратно; г) средняя скорость движения за все время пути. 4301 а) Поезд длиной 400 м прошел мимо неподвижного наблюдателя за 20 с. За сколько времени он проедет тоннель длиной 400 м? б) Поезд проехал с одной и той же скоростью мимо столба за 7 с, а вдоль платформы длиной 378 м — за 25 с. Чему равна скорость и длина поезда? ш Турист выехал на велосипеде из пункта А. Проехав 1,5 ч со скоростью 16 км/ч, он сделал остановку на 0,5 ч, а затем продолжил путь с первоначальной скоростью. Через 3 ч после выезда первого туриста из пункта А по той же дороге выехал на мотоцикле второй турист со скоростью 56 км/ч. На каком расстоянии от пункта А второй турист догонит первого? От станции А в 12 ч отправился товарный поезд. В 14 ч с той же станции вышел пассажирский поезд, который догнал товарный в 20 ч. Чему равна скорость обоих поездов, если сумма их скоростей равна 140 км/ч? Грузовик выехал из села А в 10 ч. Через 15 мин из того же села в противоположном направлении выехал мотоциклист, скорость которого была на 20% меньше скорости грузовика. Чему равны скорости грузовика и мотоциклиста, если в 11 ч расстояние между ними составило 96 км? 1^ Из города А в 9 ч 30 мин выехал автомобиль, а в 11 ч в том же направлении выехал автобус. В 12 ч 15 мин расстояние между автомобилем и автобусом составило 130 км. В котором часу автобус прибудет в пункт В, если скорость автомобиля на 40% больше скорости автобуса, и автомобиль прибыл в пункт В в 12 ч 30 мин? Катер проплыл расстояние между двумя пристанями по течению реки за 1,5 ч, а против течения — на 15 мин дольше. Чему равна собственная скорость катера, если скорость течения реки равна 2 км/ч? 100 Глава 4, § 1, п.4 Моторная лодка шла 40 мин по течению реки и 1 ч 30 мин против течения. За все это время она прошла 41,4 км. Чему равна скорость течения реки, если скорость лодки по течению на 20% больше ее скорости против течения? 43^ Теплоход проплыл некоторое расстояние по озеру за 6 ч, а то же расстояние по течению реки — за 5 ч. Сколько времени понадобится плоту, чтобы проплыть это же расстояние по реке? 438| Построй треугольник АВС по трем сторонам а, 6 и с и опиши около него окружность. 1) ._______________________. 2) ,______________———. 439| Построй треугольник АВС по двум сторонам а и & и углу С, заключенному между ними, и впиши в него окружность. а Построй треугольник ASC по стороне с и двум прилежанщм к ней углам А и В. Построй центр тяжести треугольника АВС. 1) 2) 4411 Замени данную обыкновенную дробь десятичной с точностью до целых, десятых, сотых, тысячных: ,.83. «ИО. .214 а) Т7; б) — ; в) — ; г) ■ 11′ ’39’ ’27’ ^’43 442| Трамвай проехал мимо светофора за 2 с, а по мосту длиной 175м -за 16с. Чему равна длина трамвая? 101 Глава 4, § 1, п.4 ш Находясь в пункте А на дороге, Таня увидела своего младшего брата, который появился на дороге в пункте В. Вместо того, чтобы пойти навстречу сестре, он направился в противоположную сторону, а Таня побежала за ним. Сколько минут продолжалась ♦ погоня *, если расстояние от Л до В Таня преодолела за 3 мин, а скорость брата на 60% меньше, чем у нее? Плот и яхта плывут по реке навстречу друг другу. В 15 ч 30 мин расстояние между ними было 90 км, а в 16 ч 10 мин оно сократилось до 70 км. Чему равна собственная скорость яхты? Найди квадрат разности чисел А и В: 0 (37,8 : 7,5 — 2,в • 1,4) • (-l|) + 7 : (-2|) ; 0 (7| — 8) • 3,в — 1,6 • (i -1) + 11 : (-0,35). Выполни действия и зачеркни числа в квадрате по образцу (каждое число принадлежит только одному ответу): а) 0,078 + 15,382; д) 5,872 • 0,45; е) 23,6 *3,05; ж) 15,9258:0,762; з) 18,78:37,5. б) 4,245 + 5,86; в) 7,1-6,937; г) 15,20316-9,7026; 7 1 0. 1 6 4 1. 9 0, 0 2. 2 1 8 1 5 0. 4 5. 4 6 3 5 0 5. 6 5 6 2 0 5 0 0 9 0, 8 447| в произвольном треугольнике АВС построй точку А^ — середину стороны ВС, точку В, — середину стороны АС, и точку С^ — середину стороны АВ. Построй окружности, описанные около треугольников AB^Cj, AjBC, и A,BjC. Что ты замечаешь? а) В произвольном треугольнике АВС проведи высоты AA^, ВВ, и СС^. Построй окружность, описанную около треугольника A^B^C^, и найди точки ее пересечения со сторонами треугольника АВС. Определи свойство тех точек пересечения, которые не являются основаниями высот. б) Найди отношения отрезков, на которые построенная окружность делит отрезки АН, ВН и СН, где Н — ортоцентр треугольника АВС. Что ты замечаешь? В произвольном треугольнике АВС построй центр описанной окружности — точку О, центр тяжести — точку М, и ортоцентр — точку Н. Рассмотри взаимное расположение точек О, М и Н и найди отношение отрезков ОМ : МН. Что ты замечаешь? Сформулируй гипотезу. 102 Глава 4, § 2, п.1 §2. Геометрические фигуры в пространстве 1. Пространственные фигуры и их изображение. До сих пор мы рассматривали только фигуры на плоскости — и это понятно, ведь геометрия произошла от землемерия, а значит, от исследования свойств именно плоских фигур. Но предметы окружаювцего нас мира имеют пространственную форму, поэтому в геометрии рассматриваются как плоские, так и пространственные фигуры. Из названий ясно, что все точки плоской фигуры располагаются в одной плоскости, а пространственной — нет. Наблюдаемые нами пространственные фигуры называют также геометрическими телами. Мы уже встречались с такими пространственными фигурами, как прямоугольный параллелепипед, куб, пирамида, цилиндр, шар, конус (рис.43), Цилиндр Рис. 43 Конус Пирамида Однако при исследовании свойств геометрических тел мы сразу же сталкиваемся с проблемой их изображения, поскольку зрительный образ пространственной фигуры не всегда совпадает с ее реальной формой: окружность превращается в эллипс — «сплющенную» окружность, изменяются углы между прямыми и отрезками и т. д. Поэтому вначале рассмотрим некоторые правила, позволяющие приблизить изображение пространственной фигуры к ее естественно воспринимаемому образу. На рис. 44 изображена одна и та же пирамида. В первом случае видны лишь ее передние грани, и по такому рисунку нельзя даже определить, какой многоугольник лежит в ее основании. На втором рисунке пирамида стала прозрачной — мы видим все ее ребра, грани, но по этому рисунку не ясно, как линии расположены в пространстве. Поэтому в геометрии договорились линии, которые скрыты от глаз наблюдателя, изображать не сплошными, а пунктирными, как на третьем рисунке. 103 Глава 4, § 2, п.1 Еще одно правило, помогающее сделать рисунок фигуры более понятным: на пространственном чертеже сохраняется параллельность прямых и отношение параллельных отрезков. Именно так мы всегда и поступаем, изображая параллельные ребра куба и параллелепипеда. Исследование свойств пространственной фигуры можно проводить, строя ее сечения плоскостью. А виды сечений определяются взаимным расположением геометрического тела и секущей его плоскости. Рассмотрим лишь один пример. Пусть требуется изобразить сечение куба плоскостью а, проходящей через точки М, Л/ и if на ребрах куба (рис. 45). Решить эту задачу помогает свойство плоскостей, которое мы наблюдаем ежедневно, листая книгу или тетрадь: две различные непараллельные плоскости пересекаются по прямой. Вместе с тем мы знаем, что для проведения прямой достаточно иметь любые две ее точки. Значит, наша задача сводится к нахождению двух общих точек плоскости а и каждой грани куба, которую она пересекает. М iv, 1 1 1 t 1 1 Рис. 45 Теперь обратимся к чертежу. Точки MuN принадлежат одновременно плоскости а и передней грани куба, поэтому плоскость а пересекает переднюю грань по отрезку MN (рис. 46). Аналогично пересечением плоскости а с верхней гранью является отрезок NK, а с боковой гранью — отрезок КМ. Плоскость а будто отсекает от куба один из углов, и в сечении получается треугольник MNK. В завершение заметим, что иногда для более ясного представления о фигурю (например, рис. 47) изображают ее вид спереди, слева и сверху, как бы «фотографируют» ее с разных сторон (рис. 48). Полученные «чертежи-фотографии» называют проекциями. Поэтому полезно научиться по пространственному изображению фигуры строить ее проекции, и наоборот. / Рис. 47 Вид сверху ^1^ Вид спереди Вид слева Рис. 48 Найди в окружающей обстановке предметы, имеющие форму куба, прямоугольного параллелепипеда, шара, пирамиды, цилиндра, конуса. 104 Глава 4, § 2, п.1 |45iJ Какие геометрические тела изображены на рисунке? Перерисуй их по клеточкам в тетрадь. а) На рисунках изображены фигуры, которые называются «усеченными пирамидами». Что в них общего и чем они отличаются? N б) Какие плоские фигуры ограничивают усеченные пирамиды? Какие из них являются видимыми для наблюдателя, а какие — нет? в) По аналогии с усеченными пирамидами начерти «усеченный конус». Перенеси рисунок куба в тетрадь и построй его сечение плоскостью, проходящей через точки М, N и К. Проверь правильность построения с помощью модели куба. Глава 4, § 2, п.1 ш Перерисуй пирамиду в тетрадь и построй ее сечение плоскостью, проходящей через точки М, N и К. Построй модель этого сечения из палочек и пластилина. 4551 Сложи фигуры из кубиков. Перенеси рисунки в тетрадь и дорисуй их проекции. Фигура Вид спереди Вид слева Вид сверху а) а б) в) г) 106 Глава 4, § 2, п.1 14561 По рисункам фигур изобрази их проекции. Проверь свои изображения, сложив фигуры из кубиков. .—2 457 По данным проекциям фигуры сложи ее из кубиков и нарисуй. а) б) в) г) Вид спереди Вид слева Вид сверху 4581 Закончи предложения так, чтобы получились истинные высказывания, и запиши их на математическом языке. Что объединяет эти предложения? Подбери для них общее название. а) Если каждое из двух чисел делится на некоторое число, то их сумма . б) Если одно из двух чисел делится на некоторое число, а другое — не делится на это число, то их сумма . в) Если одно из двух чисел делится на некоторое число, то их произведение. г) Если первое число делится на второе число, а второе число делится на третье, то . 4591 Сформулируй признаки делимости на 10, 2,5,3, 9, используя обороты: *если и только если*, * тогда и только тогда*, * необходимо и достаточно*. Какие два логические следования в них содержатся? Почему для их названия используется слово «признаки»? 107 Глава 4, § 2, п.1 Найди истинные высказывания и составь из соответствующих им букв название учебника по геометрии, который использовался более 2000 лет. Кто его автор? 101 285 является делителем 3 [а] 3 -140 -17 кратно 10 |н| 17 500 кратно 100 [д] 815 + 72 413 делится на 5 Гр] 3048 делится на 2 и на 9 1Е1 9 не является делителем 34 — 567 [а] 123 456 кратно 6 6402 — 78 кратно 3 рв] 54 207 не делится на 9 1 А| 279 + 1300 — 45 делится на 9 [ч] 15 не является делителем 73 510 Щ 70 707 — 160 — 23 не кратно 30 461| 1) Что значит — сократить дробь? Сформулируй определение. На какие понятия оно опирается? 2) Запиши на математическом языке основное свойство дроби. Пользуясь им, определи, увеличивается или уменьшается дробь при сокращении? 462| Найди значения выражений: л . а) 25 ’ — 5^ ’ д) . 2=*- 3^- 5 б)дз; 2^ — 3 — 5=» ’ е) 15 • 2 15’2 + 8 • 15 ’ 54 • 14- 14 • 6 . 54 — 14 + 6 — 14 ’ ж) з) — 525 2 • 5=‘’ 7 ’ 36+18-7 36-18-7 4631 Сократи дроби с натуральными числителями и знаменателями; а) б) 12аЬ. 15&=*’ 14дг отметили точку М, на ребре АС — точку 7V, а на ребре ВС — точку К (рис. 72). Построй сечение тетраэдра АВСВ плоскостью а, проходящей через точки М, N viK. 118 Глава 4, § 2, п.З 3. Тела вращения. Со времен изобретения гончарного круга люди научились создавать круглые амфоры, вазы, горшки. Их можно получить в результате вращения в пространстве некоторой плоской фигуры вокруг прямой I, которая называется осью вращения (рис. 73). В геометрии такие фигуры называются телами вращения. -1 Рис. 73 Рис. 75 Рис. 74 Простейшими телами вращения являются цилиндр и конус. Цилиндр получается в результате вращения прямоугольника вокруг своей стороны (рис. 74), а конус — в результате вращения прямоугольного треугольника вокруг своего катета (рис. 75). Само название этих тел напоминает нам о том, что геометрические фигуры являются образами предметов окружающего мира. Так, цилиндром (xhXivShoQ в Древней Греции называли валик для перемещения тяжелых грузов, конусом (xGJvoQ называли еловую шишку и предметы, похожие на нее по форме, — пробку для бочки, верхушку шлема. При сечении цилиндра, конуеа или любого тела вращения плоскостью, содержащей ось вращения, получается осевое сечение. Осевым сечением цилиндра на рис. 74 является прямоугольник АВСП, а осевым сечением конуса на рис. 75 — равнобедренный треугольник АБС. Все осевые сечения одного тела вращения равны между собой. Развертка цилиндра на плоскости состоит из двух кругов — оснований цилиндра, и прямоугольника — его боковой поверхности. В основании конуса также лежит круг, а боковая поверхность представляет собой сектор круга. Развертки цилиндра и конуса приведены на рис. 76 и 77. основания боковая поверхность основание боковая поверхность Рис. 76 Рис. 77 119 Глава 4, § 2, п.З Еще одной фигурой вращения является шар. Шар получается вращением круга вокруг своего диаметра (рис. 78). Поверхность шара имеет специальное название — сфера. У шара и сферы, так же как у круга и окружности, есть центр, радиус и диаметр (рис. 79). Особенностью сферической поверхности является то, что ее невозможно «развернуть» на плоскости. Если какая-нибудь плоскость пересекает шар, то пересечением является либо точка, либо круг. Круг, проходящий через центр шара, называется большим кругом — его радиус равен радиусу шара. По мере удаления от центра размер круга сечения уменьшается (рис. 80). Это мы можем наблюдать, например, разрезая ножом апельсин. Рис. 82 Форму, близкую к форме шара, имеют арбуз, мяч, планеты, и в частности. Земля. Сечения поверхности Земли плоскостями, параллельными экватору, -это известные всем параллели (рис. 81). Когда параллели приближаются к полюсам, их радиусы уменьшаются, а самый большой радиус — у экватора Земли, он равен примерно 6378 км. А сечения поверхности Земли плоскостями, проходящими через Северный и Южный полюсы, — это меридианы (рис. 82). 5091 а) Продемонстрируй, как с помощью 4-5 карандашей цилиндрической формы одного диаметра осуществить перемещение какого-нибудь предмета. б) Сверни из бумаги коническую поверхность и продемонстрируй, как можно использовать ее в виде пробки. Нарисуй от руки окружность и постарайся с помощью штриховки придать «объемность» получившемуся кругу. 120 Глава 4, § 2, п.З unj Практическая работа. Вырежи из картона прямоугольник, прямоугольный треугольник, круг и закрепи их на стержне (рис. 83). Вращая стержень между ладонями, понаблюдай, как образуются цилиндр, конус, шар. б) Нарисуй в масштабе 1 : 4 тело вращения и три его проекции, если оно получается в результате вращения: а) прямоугольника со сторонами 10 см и 4 см вокруг большей стороны; б) прямоугольного треугольника с катетами 6 см и 8 см вокруг меньшего катета; в) круга радиуса 6 см вокруг диаметра. Практическая работа. а) Развертка боковой поверхности цилиндра — прямоугольник, одна из сторон которого равна длине окружности основания. Проведи эксперимент, позволяющий выявить зависимость между длиной окружности С и ее диаметром d. Для этого вырежи полоску бумаги 5 см х 27 см и сверни ее в трубочку высотой 5 см. Начерти окружности с диаметрами d, = 4 см, dg = 6 см и dg = 8 см. Совмещай с ними поочередно круглое отверстие трубочки, отмечая положение конца полоски (рис. 84). : с, : с, ‘ Рис. 84 Разверни полоску и измерь отрезки, показывающие длины окружностей С^, Сд и Сд. Найди отношение соответствующих значений С и d с точностью до сотых. Что ты замечаешь? б) Вычисли с точностью до сотых среднее арифметическое полученных отношений и обозначь его л. Запиши формулу зависимости С от d. в) Найди с точностью до сотых разность полученного тобой числа л и числа 22 Архимеда —— . 121 Глава 4, § 2, п.З 514| а) Сколько больших окружностей можно провести на сфере через одну точку? Проиллюстрируй с помощью предметной модели шара. б) Можно ли провести па шаре две большие окружности так, чтобы они не пересекались? А две произвольные окружности? в) На сколько частей делится сфера одной большой окружностью, 2 большими окружностями, 3 большими окружностями, имеющими общий диаметр? 515| На сфере проведены две большие окружности (рис. 85). По рисунку можно предположить, что они пересеклись в четырех точках. А сколько на самом деле точек пересечения? 51б| Отрезок ОА на рис. 86 равен 5 см. Что можно сказать о длинах отрезков ОВ и ОС на этом рисунке? 517| Нарисуй в масштабе 2 : 1 геометрические тела, которые получаются при вращении вокруг прямой I данных фигур. Опиши их. 518| Пусть радиус основания конуса равен г, а его боковую поверхность можно «развернуть* в сектор круга радиуса R. Величина угла а этого сектора в градусах вычисляется по формуле: 360“ • г а = R Вычисли угол а и построй развертку конуса для значений г=2сми/?=5см. Вырежи боковую поверхность из бумаги и, свернув ее в конус, убедись в том, что длина дуги сектора равна длине окружности основания. 122 Глава 4. § 2, п.З 519| а) Масштаб карты равен 1:100 000. Каким отрезком на карте изображается расстояние на местности, равное 50 км? б) Запиши масштаб карты, если отрезок в 3 км на местности изображается отрезком на карте в 2,4 см. в) Рисунок сделан в масштабе 10:1. Как изменены на нем реальные размеры предметов? г) Запиши масштаб рисунка, если фигура на рисунке увеличена в 5 раз. Счет-тест (5 мин). Вариант I ^562 4)-3i-(-l|) 5) -0,5-0,06 6) 17,2-0,01 7) -3,2 : (-0,08) 8) (1-0,2)- (-|) Вариант II 1)-^+ -^+ — ^ 14 21 7 5) -2,8-0,7 6) 15,6 : 0,01 7) 3,5-(-0,04) 4)-l|-(-2|) 8)|: (-1-0,2) 2)18-(-|) 521| а) Разбей число 425 на два слагаемых пропорционально числам 2 и 3. б) Раздели число 520 на три части в отношении — 2 3 4 Акциями предприятия владеют фирмы А, В и С. Количество их акций находится в отношении 3 : 5 : 7 и составляет 60% от числа всех акций предприятия. Остальными 200 000 акций владеют работники предприятия. Сколько акций имеет каждая фирма? Три каменщика за выполненное вместе задание получили 4700 р. Первый каменщик может выполнить все задание за 3 дня, второй — за 4, а третий -за 5. Как распределить между ними выплаченную сумму пропорционально их производительности? При строительстве дома по известным размерам стен можно вычислить, сколько кирпичей потребуется для ее укладки. Для этого используется формула N = eilh, где N — количество кирпичей, 1м- длина стены и Л м — высота стены. а) Найди N, если l = S, h = 3,5. б) Найди /, если N = 2440, h = 2,5. в) Найди Л, если N = 5000,1 = 4. (Ответ округли с точностью до десятых.) В каждом случае придумай соответствующую задачу. 123 Глава 4, § 2, п.З |52j в физике при расчете сопротивления R проводника используется формула: о- I R pg, где I — длина проводника, S — площадь его поперечного сечения и р — удельное сопротивление. Вырази из этой формулы значения р, 1и8. ш Количество теплоты Q, необходимое для нагревания физического тела, можно вычислить по формуле: Q — cm(t^ — fj), где с — удельная теплоемкость вещества, т — масса тела, — начальная и

конечная температуры тела. Вырази из этой формулы значения с, т, 527| Выполни действия и упрости, если возможно, полученные выражения (значения всех переменных отличны от нуля): О . т т “’l5‘25 = * J- 2 . в) _ 7х 121/2* д: ‘ V . -5fl2 9с2 ’ 18с ■ |528| Склей из бумаги модель цилиндра, радиус основания которого равен 3,5 см, а развертка боковой поверхности — прямоугольник со сторонами 7лсм и 10 см, где л- число, равное примерно 3,14. 529| Нарисуй в масштабе 1 : 3 геометрическое тело, которое получается при вращении квадрата вокруг своей диагонали, если длина диагонали равна 12 см. Начерти три проекции этого тела. 1^ Упрости выражения и найди их значения: 2 1 ^ 4 5 5с 4с 15с 6 . Зтп бт* 1 2 «о « ^ в) и:——> если т = — ;п = -—;х = 0,8; у = -0,5. 2ху ху 6 3 |53jJ На выполнение домашних заданий у Димы ушло 2 ч. Это время он распределил между математикой, русским языком, английским языком и биологией в отношении 2:2:3: 1. Сколько времени ушло на каждый из предметов? |532| Скорость V, с которой тело движется по окружности, можно вычислить по формуле: V — 2кг где г — радиус окружности, Т — время, за которое оно совершает один полный оборот (период обращения), к — число, равное примерно 3,14. Вырази из этой формулы значения пл.Т. 124 Глава 4, § 3, п. 1 533| Раздели число 64 в отношении а : Ь, если: ф|^ 0,2 • 0,8 — 0,2 • 1,8 (-0,2)=* 534| Сделай модель конуса, радиус основания которого равен 5 см, а радиус развертки боковой поверхности — 15 см. 1535| Из 6 одинаковых квадратов легко составляется развертка куба. Можно ли из 5 одинаковых прямоугольников составить развертку параллелепипеда? §3. Геометрические величины и их измерение 1. Измерение величин. Длина, площадь, объем. Понятие величины связано с количественной характеристикой какого-либо объекта или явления. Величина может быть измерена, а результат измерения выражается числом. Примерами величин являются время, скорость, масса, температура и т.д. Нам известны также геометрические величины длина, площадь, объем, характеризующие свойства геометрических фигур. Чтобы измерить величину, нужно выбрать единицу измерения и узнать, сколько раз она содержится в измеряемой величине. От выбора единицы измерения зависит результат измерения величины: чем она больше, тем меньше значение измеряемой величины, и наоборот. Поэтому сравнивать величины и выполнять над ними арифметические действия можно только тогда, когда они измерены одной единицей измерения. Первые единицы измерения были не слишком точны. Длины измерялись шагами, ступнями, локтями, ладонями и т.д. Единицами измерения площадей служили либо участки земли, которые можно было вспахать за день, либо длины обхода этих участков -ошибочно предполагалось, что фигуры, равные по площади, имеют и равные периметры. Объемы измерялись специальными мерными сосудами, которые в разных местностях были разными. Это привело к тому, что в Германии, например, было 40 различных единиц длины — локтей, во Франции — 18 единиц длины, называвшихся лье, а в России — более 100 различных футов’, ткацкий, рабочий, землемерный, инженерный и т.д. Разумеется, такой разнобой мешал развитию торговли и промышленности; потребности практики диктовали поиски единой системы мер. Ученые выдвигали разные идеи, стремясь зафиксировать общие, единые для всех меры. Предлагалось взять за основу размеры зерен, пчелиных сот, длину маятника, делающего одно качание в секунду. Но необходимой точности добиться не удавалось. 125 Глпва 4, § 3, п. 1 _________________________________________________ Лишь в середине XIX века была создана метрическая система мер — международные эталоны единиц измерения, которыми многие страны пользуются до сих пор. Основной единицей длины в этой системе является метр — 4Q QQ^Q Q(^ часть Парижского меридиана, а единицы площади и объема согласованы с нею: за единицу площади принят квадратный метр, за единицу объема — кубический метр. При этом было решено, что отношение соседних единиц измерения должно равняться 10 или быть кратно 10. Названия мер, больших основной единицы, образуются с помощью приставок дека (десять), гекто (сто), кило (тысяча) и мирна (десять тысяч); а для мер, меньших основной, используются приставки деци (десятая), санти (сотая), милли (тысячная) и нано (миллиардная). Наиболее распространенными единицами длины, площади и объема в повседневной жизни являются: 1 км 1м 1 дм 1 см 1 мм 1000 10 10 10 1 км^ 1 га 1а 1 м^ 100 100 100 100 1 М^ 1 ДМ‘* 1 см^ 1 мм^ 1000 1000 1000 1 дм^ 1 см^ 1 мм^ 100 100 Заметим, что единица объема, равная 1 дм^, имеет и другое название — литр, В литрах обычно измеряют объемы жидких веществ. Формулы зависимостей между линейными размерами геометрических фигур, их площадями и объемами позволили перейти от непосредственных измерений площадей и объемов к вычислениям по этим формулам. Некоторые из них нам уже известны — например, формулы периметра и площади прямоугольника и квадрата, формулы площади поверхности и объема прямоугольного параллелепипеда и куба (рис. 87). а а ,, Р = 2(а +Ь) S = ab Р = 4а S = a^ Л а S = 2 ^2 I > 1 В е.. ■Н——( б) площадь прямоугольника ABCD; В . С D □ в) объем прямоугольного параллелепипеда ABCDA^BjCjDj. В, »/У/У/Л 0 / Z7 / / 7 / / / / / / V Как изменяется результат измерения величин при увеличении мерки, при уменьшении мерки? 127 Глава 4; § 3, п. 1_ 37| В каких единицах обычно измеряют: а) длину шага; б) вместимость банки; в) площадь поля; г) объем бассейна; д) площадь квартиры; е) расстояние между городами; ж) рост человека? 53^ Вырази: а) 1 дм в миллиметрах, в километрах, в метрах; б) 1 а в гектарах, в квадратных метрах, в квадратных километрах; в) 1 см^ в кубических миллиметрах, в кубических метрах, в кубических дециметрах, в литрах. [539| Заполни пропуски и прочитай полученные числа: а) 2 м 45 см = . см б) 2 м 45 см = . м в) 2 м 45 см = . дм 2 м^ 45 см^ = . м^ 2 45 см^ = 2 м^ 45 см^ = . см* 2 45 см* = . см* 2 м* 45 см* = . м* дм» 2 м* 45 см* = . дм* 5401 Вычисли разными способами площади закрашенных фигур: а) 9 см б) 3 м 4 м в) 12 мм 7 см I 2 м 3 м 2 м ________________________I I__ 8 мм 9 мм 7 мм 9 мм ___I 8 мм 1| а) Длина прямоугольника на 16 см больше ширины, а периметр равен 22,4 дм. На сколько квадратных дециметров площадь этого прямоугольника меньше площади квадрата с тем же периметрюм? б) Периметр квадрата равен 6 м, а периметр прямоугольника на 20% больше. Ширина прямоугольника в 5 раз меньше длины. На сколько процентов площадь этого прямоугольника меньше площади квадрата? 542| Выполни действия: а) 4,1 м — 3,7 дм + 72,6 см; б) 10,2 дм + 8,4 см — 0,125 м; в) 1,64 км • 30,5 — 25 км 20 м; г) 3 дм* 2 см* + 35,4 см*: 0,05; д) 1,5 м* — 1,5 дм* + 51 500 см*; е) 28,8 а : 0,48 + 5,6 га • 0,25. 543| Измерения прямоугольного параллелепипеда 36 см, 8 дм и 12 дм 5 см. Найди его объем и вырази: а) в кубических дециметрах; б) в кубических метрах; в) в кубических сантиметрах. Сравни объемы и площади поверхностей куба и прямоугольного параллелепипеда, если: а) ребро куба равно 5 дм, а измерения прямоугольного параллелепипеда 15 см, 1 м и 8 дм; б) ребро куба равно 4 см, а измерения прямоугольного параллелепипеда 0,2 дм, 3 см и 25 мм. Что ты замечаешь? |545| Объем прямоугольного параллелепипеда равен 240 см*, ширина — 5 см, а высота — на 20% больше ширины. Длину этого параллелепипеда уменьшили на 3 см. На сколько процентов уменьшился его объем? 128 tnaea 4. 3. n.1 Найди объем тела, изображенного на рис. 89, и построй три его проекции в масштабе 1: 10. 40 см а) На изготовление какого из двух аквариумов на рис. 90 потребовалось больше стекла? б) Аквариумы заполнили водой так, что уровень воды в первом аквариуме ниже верхнего края на 10 см, а во втором — на 5 см. В каком аквариуме больше воды? Сравни: а) 40 см^ и 4 дм^; 500 мм^ и 5 см^; 8000 дм^ и 8 м^; 10 000 м^ и 1 га; б) 9000 дм^ и 9 м®; 700 см“ и 7 дм*; 20 000 мм* и 2 см*; 600 000 см* и 6 м*. Из текста учебника выпиши формулы, выражающие зависимости между величинами в круге и в шаре. Пользуясь ими, реши задачи: 1) Радиус окружности равен 5 см. Чему равна длина этой окружности? Число я округли до сотых. 2) Сколько оборотов сделает колесо на участке пути в 1,2 км, если диаметр колеса равен 0,8 м? Число я округли до целых. 3) Выполни измерения и найди площади заштрихованных фигур. Число я округли до десятых. В 4) Радиус мяча равен 1,5 дм. Найди его объем и площадь поверхности. Число я округли до сотых, а полученные ответы — до десятых. |550| Во сколько раз площадь поверхности шара радиуса г больше площади круга того же радиуса? 129 Глава 4, § 3, п.1 551| Докажи, что фигуры Л, В и С равновелики (имеют равные площади):

г с’ — А в N J Г ч ч — — 552| а) Перечерти и вырежи из бумаги параллелограмм (рис. 91). Покажи, как его можно «перекроить» в прямоугольник. б) Запиши формулу для вычисления площади параллелограмма по длине его стороны а и длине перпендикуляра h, опущенного из вершины параллелограмма на эту сторону (рис. 92). 553| Назови тему и рему общих высказываний и переформулируй их, используя союз «если. то. »: а) Куб является прямоугольным параллелепипедом. б) Диаметр окружности является хордой этой окружности. Построй обратные утверждения разными способами: меняя места.ми тему и рему и меняя местами условие и заключение. Докажи, что обратные утверждения являются ложными, и построй их отрицания. 5541 Перепиши в тетрадь равенства, вставляя вместо звездочек пропущенные цифры: а) 3- -^ ^11 22 б) -..-,8 : 5 — = . 13 1 2^6 ,15 ,26-15 , 11 11 ^ ^ 22 “ «22 48 • 3 3 • 3 = *,9. 10 • ■А • 1 10 ^2 ’ 5551 Чем похожи и чем отличаются выражения? Найди их коэффициенты и буквенные части: а) (-Зл:)^, -Зх^ и (-З)^д:; 155б| Выполни действия: а) -22 : (-0,25); б) (-|) 1,8; в)(-0,5)2 • 4,8; i,)-l|:(-|)’. 130 __________________________________-______________Глава 4, § 3, п.1 22 а) Какое число нужно вычесть из числителя и знаменателя дроби —, чтобы получить число, равное 0,5? б) Некоторое число вычли из числителя, прибавили к знаменателю дроби 7 1 — и после сокращения получили —. Какое это число? Упрости выражения и найди их значения: 2 а) 5(а — 1) — (2а + 3), если а — — — ; О б) -2(1 — Щ + 4(2 — Ь), если Ь = -0,2; в) 4-|—^д:+1^| + 2х, если х = -1,5; г) 1-| +2y-(2j- у), если 4 ——- 9 [559| в произведениях Ж.Верна встречаются такие строки: а) «Аэростат несся вперед со скоростью 45 миль в час. * б) «Туземцы были ростом от 5 футов 4 дюймов до 5 футов 7 дюймов*. в) «Аппарат, напоминавший огромного кита, был длиной приблизительно в 250 футов и возвышался на 10 — 12 футов над уровнем моря. » г) «Было решено ограничить дневные переходы 15-18 милями*. Переведи выделенные величины в метрическую систему, если: 1 миля = 4448 м; 1 фут = 32,5 см; 1 дюйм = 2 см 7 мм. Заполни пропуски и прочитай полученные равенства: а) 3 м 8 см = . см; б) 3 дм 8 см = . дм; в) 3 км 8 м = . км; 3 м^ 8 см^ = . см^; 3 дм^ 8 см^ = . дм*; 3 км* 8 м* = . км*; 3 м* 8 см* = . см’^; 3 дм* 8 см* = . дм*; 3 км* 8 м* = . км*. Выполни действия: а) 7 м 25 мм- 72,5 см; б) 9 км 48 м + 3,52 км — 556 м; в) 8 см* 5 мм* • 24 + 680 мм*; г) 0,02 дм*-2,7 см*: 0,25. ш Поле имеет форму прямоугольника. При проведении землеустройства длину поля увеличили на 5%, а ширину — на треть. На сколько процентов увеличилась площадь поля? Измерения одного прямоугольного параллелепипеда равны 0,4 м, 25 см и 1,5 дм, а измерения другого параллелепипеда — 0,3 м, 2 дм и 26 см. Какой из этих параллелепипедов имеет больший объем? Какой имеет большую площадь поверхности? Докажи, что I XI ZABC Рис. 94 При измерении углов, как и при измерении любых величин, выбирают единицу измерения и устанавливают, сколько раз она содержится в данном угле. Так, на рис. 95 угол АОВ измерен различными единичными углами е^, е.^ и е^. По рисунку видно, что чем больше единичный угол, тем меньше величина угла, и наоборот. ZAOB =12е. ZAOB = В ZAOB = 4е„ Самой распространенной единицей измерения углов является градус (обо- значается 1®). Угол величиной в 1° равен 90 части прямого угла (рис. 96). Например, величина угла MNK, выраженная в градусах, равна 42″ (рис. 97). 133 Глава 4, § 3, п.2 Градусная мера угла появилась в древнем Вавилоне более 3000 лет назад и связана с шестидесятиричной системой счисления, которая тогда там использовалась. При разработке метрической системы мер в конце XVIII — начале XIX в. было предложено делить прямой угол не на 90, а на 100 частей. Угол, равный части прямого угла, назвали град, однако используется он редко. На шкале известного нам прибора — транспортира — отложены углы в 1″, поэтому с его помощью можно измерять или строить на плоскости любой угол, выраженный в градусах. Вспомним, как это делают. Чтобы измерить угол, например, АОВ, надо приложить транспортир так, чтобы вершина угла О совпала с центром транспортира, а сторона ОА прошла через начало отсчета на шкале (рис. 98). Тогда сторона ОВ укажет на той же шкале величину угла в градусах: /ЛОВ = 124°. Чтобы построить угол, равный, например, 35°, надо совместить центр транспортира с началом некоторого луча ОА — точкой О — так, чтобы луч ОА прошел через начало отсчета на шкале (рис. 99). Затем около деления выбранной шкалы с отметкой 35° надо поставить точку В и соединить ее с точкой О. Градусная мера полученного угла АОБ равна 35°: /АОВ = 35°. Отметим, что такой же угол можно построить и по другую сторону от луча QA: /АОВ^ = 35°. О [STJ Вырази величину угла АОВ в единицах измерения е^, е^, е.^, е^: а) Как изменяется результат измерения углов при увеличении единицы измерения? При уменьшении единицы измерения? б) Какими единицами измерения удобнее измерять углы — большими или маленькими? Почему? в) Какая единица измерения углов является общепринятой? Известны ли тебе другие единицы измерения углов? 134 Глава 4, § 3, п.2 [57^ Чему равна градусная мера: а) прямого угла; б) острого угла; в) тупого угла; г) развернутого угла; д) угла, вертикального углу 75°; д) угла, смежного с углом 30°? По рис. 100 определи градусные меры углов: а) АОС, AOD, АОЕ, AOF, АОК; б) ВОК, ВОР, ВОЕ, BOD, ВОС; в) COD, EOF, FOK, EOC, DOK, COF. Почему транспортир удобно прикладывать так, чтобы одна из сторон угла проходила через нулевую отметку на его шкале ? Определи на глаз величины углов и проверь себя, измерив углы транспортиром. Заполни таблицу. К Название угла Величина угла Ошибка d= а- Ь на глаз (а) измерением (Ь) ZAOB ZCDE ZKLM ZSNT Начерти луч О А. С помощью транспортира отложи от него углы 35° и 120°. Приведи все возможные варианты решения. Построй с помощью транспортира угол АВС, равный: а) 58°; б) 116». Проведи биссектрису у1’ла АВС. Построй с помощью транспортира угол CDE, равный: а) 72°; б) 150°. Раздели его на три равные части. 135 Глава 4, § 3, п.2 Построй с помощью транспортира угол MNK, если известно, что: 2 а) он равен — развернутого угла; б) 0,75 его составляет прямой угол. У 580| Построй с помощью транспортира два смежных угла, если один из этих углов: а) на 28° больше второго; б) в 5 раз меньше второго; в) составляет 25% второго; г) на 40% больше второго; д) на 20% меньше второго угла. 581| 1) Найди 110 рисункам, не выполняя измерений, величину угла ЛОВ (на каждом рисунке равные углы обозначены одинаковыми дугами): г) О D 2) Сколько на каждом из рисунков острых углов (л:), прямых углов (у), тупых углов (г), развернутых углов (#)? Ответ дай в виде четырехзначного числа xyzt. В треугольнике АВС угол А равен 36°, а угол В равен 84°. Биссектрисы углов А и С пересекаются в точке О. Найди величину угла АОС, считая сумму углов треугольника равной 180°. 1) Построй четырехугольник АВС£) по координатам его вершин: А (-4; 0), В (2; 3), С (5; 0), D (0; -8). Измерь углы четырехугольника АВСВ и найди их сумму. 2) Начерти два произвольных четырехугольника и измерь их углы. Сравни полученные результаты и сделай вывод. Можно ли распространить этот вывод на любой четырехугольник? Почему? 3) Начерти произвольный четырехугольник и проведи его диагональ. Сколько получилось треугольников? Как связаны между собой углы этих треугольников и углы данного четырехугольника? Закончи предложение: €сии о/мма tftuoS iHfieifioubHUKa ра£на fifO «. tfio сумма углов 4eifibtfiexyioxbH.UKa (гавна_______. Будет ли это предложение истинным для любого четырехугольника? Почему? 136 Глава 4, § 3, п.2 |584| Построй треугольник АВС, используя линейку с делениями и транспортир, если: а) АВ = 5 см, ВС = 3,5 см, ZB = 76°; 6) АС = 4 см, ZA = 32°, ZB = 58°; в) АВ = б см, ZA = 47°; г) ВС = 3 см, ZB = 110°, ZC = 24°. Какие из приведенных задач имеют единственное решение? По рис. 101 объясни способ деления окружности на 5 равных частей с помощью транспортира. Раздели тем же способом окружность: а) на 6 равных частей; б) на 9 равных частей. Рис. 101 а) Ученикам 6 «А* класса был задан вопрос: «Какое из следующих занятий тебе нравится больше всего: чтение, спорт, прогулка, просмотр телевизионных передач?* При этом каждый выбирал только одно из этих занятий. Проанализируй результаты опроса с помощью круговой диаграммы (рис. 102). Измерь транспортиром углы секторов диаграммы и определи, сколько человек выбрали каждый ответ, если в 6 «А» всего 24 учащихся. б) Тот же вопрос в 6 «Б* классе дал следующие результаты: № Выбранный ответ Число учащихся 1 чтение 9 2 спорт 8 3 прогулка 6 4 телевизор 7 Построй круговую диаграмму и сравни вкусы учащихся обоих классов. в) Проведи в твоем классе аналогичный опрос, построй круговую диаграм му и проанализируй полученные результаты. [58Т| Перенеси рис. 103 в тетрадь. Построй без транспортира, используя клеточки, угол в 90», одной из сторон которого является: а) луч АВ; б) луч CD. Сколько градусов содержит угол между часовой и минутной стрелками часов в 3 ч, 6 ч, 8 ч, 10 ч, 11 ч, 14 ч 30 мин? Рис. 103 137 Глава 4, § 3. п.2 5891 Вычисли устно и найди следующее число в ряду ответов при условии сохранения закономерности: 9,1 0,8 -0,4 -26 0,7 : 13 •1,2 -0,8 + 17 : 0,2 + 0,9 : 0,16 •3 :(-6) + 1,5 •2,5 -4,8 t 1,6 -3 •0,08 -2,8 •0,5 : (-20) •0,2 -1 ? ? ? ? ? 5901 Запиши выражение и найди его значение при данных значениях букв: а) модуль числа, противоположного удвоенному произведению чисел аи Ь (а = —|;Ь = -1,4); б) сумма модулей чисел с и d (с = -0,8; d = 0,7); в) модуль разности частного чисел m и п и утроенного числа к(т= 1,6; п = -3, k = -0,4). Переформулируй предложения, используя союз «если. то. ». Докажи, что обратные утверждения являются ложными, и построй их отрицания: а) Четырехугольник является многоугольником. б) Квадрат отрицательного числа положителен. 592| Где расположена на координатной плоскости точка М (х; у), если: а) X > о, у > 0; в) х 0; д) х > 0, у -а>0; в) V х е Q: х -^>1; r)Vj/eQ: t/^=*l => |г/| = 1. Верны ли обратные утверждения? Какие утверждения равносильны? Запиши их и прочитай разными способами. 622 Заполни таблицу и сделай вывод. Запиши его на математическом языке. а 12 7 -5 4 0,9 2,5 0 Ъ 3 8 2 -6 1.4 0,7 -5 а-Ь Ь — а 623| Вычисли устно, если т ^ п: 3 3-^ , 1,2-0,12 33 0.12-1,2= 33 Найди значения выражений: а)(-1)Ч-1)Ч-1)'(-1)^ . (-1)2«о«; в) 56 4,56 г) 4,56- 56 78,9-7| 7| -78,9 Д) т- п п- т б)(-1)Ч-1)Ч-1)Ч-1Г . (-1) 2009. 625| Реши уравнения: а) I л: I = 2,5; в) | л: 4-5 | = 0; б) I л: I = -4; г) I 2д: — 3 I = 0; в) + (-2)=*««»; г) 52“°в -Ь (-5)2о«9; д) I д: — 2 I = -3; е) I д: + 11 = 5; д) ,999. 9 : 99; «У—‘ 100 цифр е) 999. 9 : 999. 9. ‘ у ‘ у ‘ 100 цифр 50 цифр ж) I 4 — Зх I = 2; з) I 2з: + 7 I — 1. ш Составь равенства, используя взаимосвязь условий. Какие задачи можно составить по этим условиям? Поставь вопросы так, чтобы решение задач было одинаковым. а) Катер плыл 4 ч по реке со скоростью х км/ч и 2 ч по озеру со скоростью на 3 км/ч большей. Весь путь составил 78 км. б) В зале расставили 78 стульев. В первых четырех рядах было по х стульев, а в каждом из двух остальных рядов — на 3 стула больше. Придумай другие задачи, которые решаются так же. 146 Глава 4, § 4, п.1 Приведи примеры величин, которые связаны зависимостью а = Ьс. Построй математические модели задач, используя табличный способ записи условий. Придумай задачи с другими величинами, которые решаются так же. а) На 160 р. можно купить тетрадей в линейку на 2 больше, чем в клетку. Сколько тетрадей каждого вида можно купить, если тетрадь в линейку на 4 р. дешевле, чем тетрадь в клетку? б) В каждом из двух домов по 112 квартир. Однако в первом доме на каждом этаже на одну квартиру больше, и поэтому число этажей в нем на 2 меньше, чем во втором. Сколько этажей в каждом доме? в) Первый автомат упаковывает в минуту на 3 пачки печенья больше, чем второй. Первому для упаковки 600 пачек печенья требуется на 10 мин меньше, чем второму. Сколько пачек в минуту упаковывает каждый автомат? |628| а) Проанализируй ритмическую структуру нескольких строк какого-нибудь стихотворения. Наблюдается ли в них симметрия? Приведи несколько примерюв симметрии из разных областей жизни, б) Согни полоску бумаги несколько раз пополам, вырежь по контуру элемент орнамента и разверни, как показано на рисунке. Какие виды симметрии можно наблюдать в получившемся орнаменте? /А. Ж >0. ^ в) Согни последовательно лист бумаги, как показано на рисунке. Сделай вырезы на заготовке и разверни. Что получилось? Какими видами симметрии обладает получившаяся фигура? 6* Глава 4, § 4, п.1 1629I Выполни построения и проверь их правильность с помощью кальки: а) Перенеси рисунок в тетрадь и построй фигуры, симметричные данным относительно прямой Г. б) Покажи на чертеже оси симметрии и центр симметрии прямоугольника. в) Перерисуй орнамент в тетрадь и продолжи его. Какие виды симметрии можно наблюдать в этом орнаменте? г) Придумай и нарисуй свой орнамент. Реши уравнения: а) I д: I = 3,6; б) | 2д: + 9 | = 0; в) | Зх — 1 | = 5; г) I 7-х| = -2. 6321 Вычисли: У лисы Алисы в 5 раз больше монет, чем у кота Базилио. Если она подарит ему 16 монет, то монет у них станет поровну. Сколько монет у каждого? а) i-(- ir-(i r) 0,1-0,12-0,18; 6)-i+l (-ir- (-1)” Д) -0,1+(-0,1)2+ (-0,1)8; f 1V в)-з-| (-3) -1 h)’ e) -0,1-(-0,1)2-(-0,1)8. Построй математическую модель задачи: «Дядя Федор должен был проехать 30 км, чтобы успеть к поезду. Однако из-за кота Матроскина он задержался с выездом на 20 мин. Чтобы приехать на станцию вовремя, он ехал со скоростью на 3 км/ч большей, чем предполагал. С какой скоростью ехал дядя Федор?* 148 Глава 4, § 4, п.2 о Слово СЕНО имеет горизонтальную ось симметрии, а слово ШАЛАШ — вертикальную. Кроме того, слово ШАЛАШ является палиндромом — при чтении его справа налево получается то же самое слово. Палиндромом является также предложение АРГЕНТИНА МАНИТ НЕГРА. Придумай свои примеры симметричных слов и палиндромов. Сколько плоскостей симметрии имеют: а) прямоугольный параллелепипед; б) куб; в) конус; г) цилиндр; в) шар? 2. Преобразования плоскости. Равные фигуры. В предыдущем пункте мы разобрали вопрос о том, как выяснить наличие или отсутствие разных видов симметрии фигур по рисунку. Но для математиков рисунок — это только иллюстрация, и поэтому нужно сначала дать точное определение видов симметрий на математическом языке, а в нем нет слов «перегнуть», «передвинуть», «вырезать». Чтобы перейти от рисунка к определению, как мы уже знаем, нужно выявить характеристические свойства точек во всех видах симметрии. И вот здесь будет необходим наш ^ опыт работы с симметричными фигурами. о— Перегибая лист бумаги по оси симметрии /, мы наблюдаем, что отрезок AA^ перпендикулярен прямой / и отрезки AM и А^М равны (рис. 113). В результате приходим к следующему определению: / J. М Рис. 113 Точки А и А,, не принадлежащие прямой I, называются симметричными относительно I, если отрезок АА, перпендикулярен этой прямой и делится ею пополам. При повороте вокруг точки О все точки плоскости движутся по окружностям с центром О, а значит, их расстояние до точки О не меняется. Кроме того, постоянными остаются угол поворота и направление поворота. Чтобы учесть направление поворота, углы поворота условились выражать рациональными числами: положительными — против часовой стрелки, а отрицательными — по часовой стрелке (рис. 114 а, б). Точка Aj называется результатом поворота точки А вокруг центра О на угол а, если: 1) ОА = ОА,; 2) Z AQAj = а. 149 Глава 4, § 4, п.2 Центральная симметрия является частным случаем поворота, когда угол поворота равен 180°. Особенностью центрально-симметричных точек является то, что они не только равноудалены от центра О, но и лежат на одной прямой с ним. Таким образом, построение упрощается: для нахождения точки А,, симметричной точке А относительно центра О, уже нет необходимости строить угол AOAj, а можно просто провести прямую ОА и отложить на ней отрезок ОА,, равный отрезку ОА (рис. 115). Точки А и Aj называются симметричными относительно точки О, если О является серединой отрезка АА,. При параллельном переносе все точки движутся по параллельным прямым. При этом они смещаются в одном направлении и на одинаковое расстояние. А это означает, что векторы AAj и d равны (рис. 116). Итак, Рис. 116 Точка Aj называется результатом параллельного переноса точки А на вектор d, если вектор AAj равен вектору d. Полученные определения позволяют строить с помощью чертежных инструментов точки-образы во всех рассмотренных преобразованиях. А значит, мы можем строить теперь преобразования фигур более точно, не прибегая к перегибаниям листа, вырезанию фигур из бумаги и т.д. На рис. 117 показано, как построить треугольник AjB,С,, в который переходит треугольник АВС при осевой симметрии (а), центральной симметрии (б), повороте на угол 120° (в) и параллельном переносе (г). _______________________________________________________/лава 4, § 4, n.2 Все описанные преобразования плоскости обладают важным общим свойством: в результате их выполнения получаются фигуры, которые можно совместить наложением, то есть равные фигуры. А значит, для обоснования равенства фигур достаточно показать, что эти фигуры могут быть получены друг из друга в результате данных преобразований. В Например, из того, что в равнобедренном треугольнике АВС медиана BD, проведенная к основанию, является осью симметрии, следует, что треугольники ABD и CBD равны, и поэтому равны их стороны и углы: AD = DC, Z1 = Z2, Z3 = Z4 = 90”(рис. 118). Значит, медиана, проведенная к основанию равнобедренного треугольника, является одновременно его биссектрисой и высотой! Таким образом, симметрия фигур помогает устанавливать разнообразные геометрические факты без непосредственных построений и измерений. А это является новым мощным инструментом как для познания природы явлений, так и для решения практических задач. [636| Перегни лист бумаги по прямой I и проткни его ножкой циркуля. Разверни лист и обозначь полученные точки буквами А и А,. Найди их характеристическое свойство и сформулируй определение точек, симметричных относительно прямой I. Сравни свое определение с определением на стр. 149 учебника. 637| Для проведения перпендикуляра к прямой часто используют чертежный угольник, как показано на рис. 119. т На бумаге без клеток начерти прямую I и отметь точку А ^ I. Построй точку А J, симметричную точке А относительно прямой I: а) с помощью чертежного угольника; б) с помощью циркуля и линейки (без делений). 63^ Перенеси рисунок в тетрадь и построй отрезок А^В^, симметричный отрезку АВ относительно прямой I. Глава 4, § 4, п.2 — ——- ——————- Ш Построй окружность, симметричную данной относительно прямой I, если: а) прямая I не имеет с окружностью общих точек; б) прямая I касается окружности; в) прямая I пересекает окружность в двух точках. |б^ Перечерти фигуры в тетрадь в масштабе 2 : 1 и проведи их оси симметрии: ш На бумаге без клеток начерти тупоугольный треугольник и построй симметричный ему треугольник относительно прямой I, содержащей: а) большую сторону; б) меньшую сторону; в) медиану, проведенную к его меньшей стороне. Отметь на кальке точки О и А и поверни кальку вокруг точки О на угол а. Чем определяется положение точки , полученной в результате поворота точки А? Сравни свои выводы с определением поворота на стр. 149 учебника. Воспроизведи чертеж и поверни: а) точку А на угол а = -80“; б) отрезок АВ на угол а = 100°; в) треугольник АВС сначала на угол а = 90”, а потом на угол а = -90°. Что можно сказать о полученных треугольниках? а) —П О А бй| Скопируй рисунок в тетрадь и построй отрезок, симметричный отрезку АВ относительно точки О. б)[ ГМ i i О f у—’— 1 iT I

в) ‘ A Б Начерти на бумаге без клеток произвольный треугольник АВС. Построй треугольник, симметричный треугольнику АВС: а) относительно точки О, лежащей вне треугольника АБС; б) относительно середины М стороны ВС; в) относительно вершины А. 152 Глава 4, § 4, п.2 Точка О — центр симметрии шестиугольника ABCD^lM (рис. 120). Назови точки, симметричные точкам С, К, D, М относительно точки О. Какая фигура симметрична относительно точки О отрезку ВО, треугольнику АОМ, четырехугольнику AOiCM, ломаной BODK, семиугольнику ABOCJDiiL’M? На рисунке 121 изображена часть фигуры, центром симметрии которой является точка О. Начерти эту фигуру в тетради. Точка А при параллельном переносе на вектор d переходит в точку Aj. Что означает равенство AAj = d? Сделай чертеж. Начерти в тетради параллелограмм ABCD. Построй фигуру, которая получится в результате параллельного переноса этого параллелограмма: а) на вектор ВС; б) на вектор DB; в) на вектор АО, где О — точка пересечения диагоналей параллелограмма ABCD. а) Если перемещать одну из сторон чертежного угольника вдоль линейки, то, проводя прямые вдоль другой его стороны, можно получить параллельные прямые (рис. 122). Построй указанным способом несколько параллельных прямых. Рис. 122 б) Начерти на гладкой бумаге произвольный треугольник АВС и вектор d. Построй параллельный перенос треугольника АВС на вектор сГ. Имеют ли отрезок, прямая, луч оси симметрии и сколько? Имеют ли они центры симметрии? Проиллюстрируй с помощью рисунков. Начерти фигуру, которая: а) имеет и центр, и ось симметрии; б) не имеет оси, но имеет центр симметрии; в) не имеет центра, но имеет ось симметрии. 153 Глава 4, § 4, п.2 653| Построй фигуры, симметричные сектору круга (рис. 123, а) и сегменту круга (рис. 123, б) относительно точки О. Рис. 123 Проведи на бумаге без клеток прямую I и ломаную ABCD, которая пересекает прямую Г. а) в одной точке; б) в двух точках. Построй фигуру, симметричную ломаной ABCD относительно прямой I. Начерти отрезок АС и построй его серединный перпендикуляр I. Отметь на прямой I точку В и проведи отрезки АВ и ВС. Пользуясь свойствами симметрии, докажи, что: а) треугольник АВС — равнобедренный; б) углы при основании треугольника АВС равны; в) медианы, проведенные к боковым сторонам треугольника АВС, равны. Начерти отрезок АВ и отметь точку О т-п; г) 3х,у ^Q: ху 1 и С на рисунке являются вписанными в окружность, а углы BuD-нет. Придумай определение угла, вписанного в окружность. С D Построй с помощью циркуля и линейки треугольник ЛВС: а) по двум сторонам а и 5; б) по трем сторонам а, 5 и с; в) по двум сторонам а и 6 и углу между ними С; г) по стороне а и двум прилежащим к ней углам В и С (стороны и углы задай произвольно). Сколько решений имеет задача? Всегда ли решение возможно? 167 Глава 4, Ь 4, ii.4 [72^ Найди множество корней уравнения: а) -5х + 7 = 4х — 8; в) 3(5 — 2z) — 4(2 + 6) = -5(2г + 3); б) — Zj + 1,5 = у ; г)-0,7х- 2(0,4х- 2,8) = -1,6 + 3(

0,5х + 2,4). 727| Катер за полчаса по течению реки и 1 ч 20 мин против течения проплыл 58 км. Какое расстояние проплывет по этой реке плот за 2 ч 40 мин, если 2 скорость катера против течения на 16—% меньше его скорости по течению? О 7281 в 11 ч 35 мин из Москвы по Рижскому шоссе выехал автобус со скоростью 75 км/ч, а в 12 ч 15 мин вслед за ним выехал автомобиль, скорость которого на 28% больше скорости автобуса. Через сколько времени после своего выезда автомобиль обхюнит автобус на 20 км? 7291 Составь выражение и найди его значение при данных значениях букв: а) Килограмм сметаны стоит а руб., а килограмм сыра на 50% дороже. Сколько стоит покупка 200 г сметаны и 400 г сыра? (а = 60) б) Цена акций некоторого предприятия сначала увеличилась на 10%, а затем уменьшилась на 10%. Сколько стала стоить акция, если ее прежняя цена Ь руб.? (Ь = 500) в) Самолет пролетел х км, а осталось ему пролететь у км. Сколько процентов всего пути составляет оставшийся путь? (х = 480, у = 720) Запиши значение выражения в виде бесконечной периодической дроби: (1,47:1,4-1,5)*(-з|):(-2,7) а) — 0,12 • 0,5 + 0,12 б) ( 18^ 12′ ^ 6 ^30 |732| Начерти параллелепипед ABCDA,BjC,Dj и назови: а) одно его видимое и одно невидимое ребро; б) одну видимую и одну невидимую грань. Вычисли его объем и площадь поверхности, если АВ = 5 м, AD = 6 м, АА = 4 м. 732| Начерти в масштабе 1 : 4 три проекции тела, изображенного на рис. 143, и вычисли его объем, если АВ =АА^ =AF = 20 см, ВС =12 см, CD = 8 см. 733| Построй на координатной плоскости треугольник АВС, если А (-2; -5), В (0; 3), С (8; 5). Измерь стороны и углы треугольника АВС и определи его вид. Е, Построй треугольник АВС, используя линейку с делениями и транспортир, если: а) АВ = 6 см, ВС = 4 см, ZB = 56”; б) ВС = 5 см, ZB = 105°, ZC = 32”; в) АС = 4,5 см, ZA = 74”. Сколько решений имеет каждая задача? 168 Глава 4, § 4, п.4 Л ^3 . -2^^=( 4-i 1^’ ,^6 Реши уравнения: ^9л:-15 7-5х а) ;—; 736| Лучи, исходящие из вершины развернутого угла, делят его на 4 части. Пер- 5 о вый угол относится ко второму как 2,4 :1Y , третий — на 15“ меньше первого, а четвертый — в 3 раза больше третьего. Найди величины этих углов и сделай чертеж. Граница арены цирка имеет длину 40,8 м. Пользуясь формулами, приведенными на стр. 127, найди диаметр и площадь арены. Число я округли до целых. Опытный дрессировщик может вымыть слона за 40 мин, а его сын — за 2 ч. За сколько времени они вымоют трех слонов, работая вместе? Выполни действия: а) (14 м 2 см — 9 дм 64 мм): 6,4 + 0,36 м; б) (3,24 а • 0,125 — 134 дм^ 40 см^): 7,8 — 0,00045 га; в) (17,5 дм=^ • 400,8 — 3,216 м^: 1,6): 1,39 + 7 200 000 см^ 7401 Составь формулы для вычисления периметра многоугольника: а) а X б) т в) а п Составь формулы для вычисления площади фигуры: а) _____________ б) 7421 Составь формулы для вычисления объема фигуры: а) ^—— а 169 Повторение Задачи на повторение. Начерти диаграмму Эйлера-Венна множеств: N — натуральных чисел; Z — целых чисел; Q — рациональных чисел; М — отрицательных чисел. Отметь 15 2 на этой диаграмме числа: —; -2; 1—; О; 4,.5; 7; -8 — . о 1о У Найди наименьшее натуральное число, кратное 36, в записи которого встречаются все 10 цифр по одному разу. Сформулируй алгоритм сравнения рациональных чисел. Сравни дроби yj и (“■^) пятью различными способами. Среди обыкновенных дробей найди те, которые можно представить в виде конечных десятичных. Расположи их в порядке возрастания и сопоставь соответствующим буквам. Что означает полученное слово? J. _± А А _1Р Jl М 14 60 5 12 58 24 25 45 300 56 ®®©©©©®®@® Можно ли сравнить на множестве рациональных чисел: 1) tt и -а; 3) а и а-Ь 2; 5) а и а-2; 7) а и а^; 4) а и 2а; 6) с и а : 2; 8) (-а)2 и -а2? 2) а и а Сформулируй определение числа, противоположного данному, и числа, обратного данному. Запиши числа, противоположное и обратное: а) числу х б) кубу числа У’, в) сумме чисел а и 6; г) разности чисел тип. Прочитай высказывания, докажи или опровергни их. Построй отрицгшия ложных высказываний. а) V X е Q: х + (-х) = 0; в) V а е Q: -а 0,06 (-1,2) 0,024 (-|)-5,6 г) 2,47: 0,26-(-5^: 5^)’ 11 11- Сформулируй и запиши в общем виде следующие свойства рациональных чисел: а) переместительное, сочетательное и распределительное свойства сложения и умножения; б) свойства числа 0 при сложении и вычитании; в) свойства чисел 0 и 1 при умножении и делении. Придумай примеры, в которых использование этих свойств упрощает вычисления. 757| Вычисли наиболее рациональным способом: а) 11,9-1^-1^ -3,9; б) -0,48*1-| — 0,48; в) -1,62+ l|* 4,1; г) -4,35 — 2^ — 5,18 + 1^ — 4| + 5,18; д) -12,5 • (-^) • 0.8 • (-2,5) • 0,4 • (-0,52); е) -3,7 • (I — 0,125) • (-бЦ) • 34,02. Что называется отношением двух чисел? Прочитай и упрости отношения: »)0.7^2.1:2.8; г)1.05;4|; 1 5 а) Раздели число 700 в отношении 3*^ : 0,5 : . 3 6 б) Выполни действия и раздели полученное число в отношении 0,1 : 0,7: 1,6-1,6*3^ (1,3- 1,236: 1,2): (-0,03) * I 171 Повторение Периметр треугольника АВС равен 16,8 см. Найди длины его сторон, если АВ относится к ВС как 7 : 5, а ВС относится к АС как 3:4. Сформулируй определение и основное свойство пропорции. Приведи примеры. Какие преобразования пропорций возможны? а) Приведи примеры прямо и обратно пропорциональных величин. Сформулируй их определение и запиши формулы прямой и обратной пропорциональностей. б) Построй на одной координатной плоскости графики зависимостей величин у = 2х и у = -2х. Что ты замечаешь? в) Построй на одной координатной плоскости графики зависимостей величин у = — и у = — — . Что ты замечаешь? а) На ипподроме лошадь, пробежав по кругу 8 раз, преодолевает 12,8 км. Сколько километров она преодолеет, пробежав по кругу 16 раз, 20 раз? б) Две одинаковые трубы наполняют бассейн за 12 ч. За сколько времени наполнят бассейн 4 такие же трубы, 5 таких же труб? в) Автомобиль может проехать расстояние между двумя городами, двигаясь со скоростью 80 км/ч, за 6 ч. На сколько он должен увеличить скорость, чтобы преодолеть это расстояние за 4 ч? На карте, выполненной в масштабе 1 : 1 000 000, расстояние от Москвы до Орехово-Зуево равно 9 см. Чему оно равно в действительности? Каким отрезком изобразится это расстояние на карте масштабом 1: 300 000? 7651 Реши уравнения: а) 5х + 1,6 3,9 2jc-0,8 2,6 б) 2у-3 ^ 4 ’ 0,81/+1- “3,75 Как найти: а) процент от числа; б) число по его проценту; в) процентное отношение двух чисел? Придумай и реши задачи на эти правила. Затем эти же задачи реши методом пропорций. Какой способ решения ты считаешь более удобным? Почему? а) Сплав состоит из меди, цинка и свинца. Медь составляет 54% сплава, а цинк — 26% сплава. Сколько меди и цинка входит в сплав, содержащий 0,8 кг свинца? б) Из 0,2 т винограда получается 64 кг изюма. Какой процент своей массы теряет виноград при сушке? в) Морская вода содержит 5% соли. Сколько килограммов простой воды нужно добавить к 24 кг морской воды, чтобы процентное содержание соли в ней стало равно 2% ? Поезд прошел 25% всего пути, а потом 40% оставшегося расстояния. Сколько процентов всего пути ему еще осталось пройти? 172 Повгорание При изготовлении сока из апельсинов 60% массы уходит в отходы. Что дешевле — купить апельсины по цене 60 р. за килограмм и сделать из них килограмм сока или купить свежий апельсиновый сок по цене 300 р. за килограмм? На сколько процентов дешевле? Длина прямоугольника в 4 раза больше ширины. Длину прямоугольника уменьшили на 20%, а ширину увеличили на 20%. На сколько процентов изменились периметр и плош;адь прямоугольника? Запиши выражение и найди его значение при данных значениях букв: а) разность куба числа а и утроенного произведения квадрата числа Ь на число с (а = -2; Ь = 0,5; с = -0,4); б) квадрат суммы удвоенного числа х и частного чисел у г (л: = -1,5; У 1д,2 g). Назови коэффициенты и буквенные части выражений: а) -5аЬ; б) 0,3дг^; в) т^п; г) -у; д) -26 • (-0,6с). Раскрой скобки и приведи подобные слагаемые: а) 2(7 — Зл:) + 4х — 9; в) 9т — 4(2/п + п) + 2(-т f Зл); б) а(у + 6) — у(а — 1) — 6а; г) 2а^ — а(3а — 6) — Ь <а — Ь). Найди множество корней уравнения: а) 2(3х + 4) = 20 — 6(2 — х); в) 7х — 4(2х + 3) = 4х^ = 25; в) | х [ = 5 => б) х^ = 25 => X = -5; г) х^ = 25 => | х | = 5. Три маляра покрасили забор за а ч. Первый маляр, работая один, может покрасить этот забор ■ 6 ч, а второй — за с ч. За сколько времени покрасит этот забор третий маляр, если будет работать один? а) Реши уравнение методом проб и ошибок: Зх(х + 1)(х — 1) = 0. б) Реши уравнение методом перебора: 5х(х — 1)(6 — х) = 120, где х N. 173 Как мы рассуждаем, или Вместо заключения Когда люди разговаривают, они не только сообщают друг другу некоторую информацию, но и определенным образом обосновывают свое мнение. Это начинается с раннего детства, и когда мама предлагает сварить ребенку манную кашу, а он говорит: «Не надо, потому что я ее не люблю», то в его потому что уже содержится логика. Ребенок рассуждает примерно следующим образом: «Я не люблю манную кашу, следовательно, я не буду ее есть. Никто не хочет работать напрасно, значит, и мама тоже. Но если она сварит кашу, то работа будет напрасной. Если человек работал напрасно, он огорчается. Я не хочу огорчать маму, поэтому и говорю «не надо». Если же мама скажет, что манную кашу надо есть, чтобы быстрее расти, то за этим «чтобы» тоже скрывается логика: «Ребенок, который ест манную кашу, быстрее растет, а ты хочешь быстрее расти, поэтому ты должен ее есть». Чем закончится диалог — неизвестно, но уже первые фразы показывают, что это «уважительный диалог», где мама не приказывает, ребенок не капризничает, но каждый из них объясняет, аргументирует свое поведение. А могло быть и так: Мама: Я сварю тебе манную кашу. Ребенок: Не хочу. Мама: Нет, надо. Какой диалог с мамой вы бы предпочли — логически обоснованный или командно-капризный? Историки считают, что математика в Древней Греции зародилась с развитием демократии — политическом строе, где человека надо убеждать, в отличие от тирании — строе, где человеку достаточно приказывать. Но уважительный диалог возможен, когда люди придерживаются одних и тех же правил, и это прежде всего правила логики. Фактически правила логики усваиваются через язык с раннего возраста, но математика учит их применять более осознанно. Общие правила логических рассуждений впервые описал один из величайших ученых в истории человечества — древнегреческий философ Аристотель. Это было примерно 2350 лет назад. Формулируя эти правила, Аристотель опирался на человеческую практику, на естественный язык. Если, например, известно, что: 1) Все ученики 125 й школы изучают английский язык, 2) Сережа Марков учится в 125-й школе, то сразу можно догадаться, что Сережа Марков изучает английский язык. Это и есть вывод, логическое следствие из данных утверждений, а сами исходные утверждения в науке логике называются посылами. А вот из посылов: 1) Все ученики 125-й школы изучают английский язык, 2) Сережа Марков изучает английский язык нельзя сделать вывод, что Сережа Марков учится в 125-й школе, — ведь не только в этой школе изучают английский язык. 174 Аналогичные умозаключения можно выводить независимо от содержания высказываний. Например, из посылов: 1) Все галбейны рыжие, 2) Вордик галбейн следует, что Вордик рыжий, а из посылов: 1) Все галбейны рыжие, 2) Вордик рыжий не следует, что Вордик галбейн. Казалось бы, весь этот пример — какая-то чепуха, поскольку речь в нем идет о несуществующих предметах. Но что изменится в рассуждениях, если галбейна-ми назвать породу собак, а Вордиком — одну из собак этой породы? Ровным счетом ничего. Значит, правила логического вывода зависят не от конкретных понятий, а от логических связей между ними, и именно поэтому их можно распространить на любую науку и любую сферу человеческой деятельности. Вспомним, например, как успешно применял правила логического вывода Шерлок Холмс. Вместе с тем накопленных нами знаний пока не всегда хватало для безупречного использования правил логического вывода. Поэтому порой мы применяли так называемую неполную индукцию — переход от одного или нескольких примеров к общему выводу. Так нами были «доказаны* признаки делимости натуральных чисел, свойство биссектрис треугольника и др. Этот же путь прошла в своем развитии и сама наука математика: путь наблюдений, выявления различных закономерностей, выдвижения гипотез и поиска способов их доказательства. Гениальным открытием в истории математики был аксиоматический метод. Александрийский геометр Евклид, живший в III веке до н. э., блестяще использовал этот метод, сведя вместе результаты, полученные многими поколениями ученых. В своей книге «Начала* он построил геометрию, в которой любое рассуждение строится как строгая последовательность логически обоснованных выводов. Эта Евклидова геометрия и составляет основу современного школьного курса геометрии, который вы начнете изучать в 7 классе. Многие свойства фигур, которые вы будете рассматривать в курсе геометрии 7-9 классов, вам уже встречались, но лишь на уровне исследования и выдвижения гипотез. Следующий этап — доказательство или опровержение этих гипотез — поможет вам освоить новый метод логического обоснования общих утверждений -дедукцию. Дедуктивный метод базируется на получении системы обоснованных выводов из согласованных утверждений (аксиом). Поэтому он используется не только в геометрии, но и во всех разделах математики, в том числе и в алгебре, которая также изучается в старших классах. И, несмотря на то что геометрия и алгебра имеют разные предметы исследования — геометрия изучает пространственные формы тел, а алгебра — количественные отношения, общим фундаментом алгебры и геометрии являются законы логики. Мы желаем вам успехов на пути познания математических закономерностей окружающего мира и будем рады, если наша совместная работа поможет вам в этом. Авторы 175 Ответы Глава 3. S3. 16. а) а + Ь + с 3 ч 5d — . 20. а) а — -30. 21. 5. 25. 50 коп. и 24 р. 50 коп. 26. 2 : 1. 33. б) -9. 37. 12. 38. в) -0,8п*; г) зД 39. б) -2а + 1. 56. б) 25%; г) 33%; е) 60%. 57. а) Ув. 100%; б) ув. 200%; в) ум. 75%; д) ум. 25% с) ув. 50%. 58. г) 1,54л р.; д) 2.5А р. 60.80 р. 61. а) 1,75; в) 15.62. в) -х + 2; г) 5у. 63. а) 9.64. в) Ув. иа 25%. 65. . 66.0,02.67. в) 3.68. 2 полушки. 80. а) -3.81. б) 14.82. б) Q; д) ; е) (-1; -5>. 83. а) 12; -8.84. 2. 85. 1480 фунтов. 105. а) 8; б) 7.5; в) 1,5; г) 25. 106.а);г)(2>;е);ж)«. 108. 24 л и 12 л. 109. 840.110.17,5 т. 113. а) 2”. 114.84.135. а) 3; б) 10,8; ж) Зс. 137. а) На 60%; б) на 150%. 141. а) 7. 142. в) S = об — Зс’. 149. а) 105 марок. 150. 500 т. 151. 75 кг. 152. 2,4 м’. 15,3. а)^; г) . 154.4 км/ч, 30 мин. 156. а) 0,72.158. Да. 160.50.161.2,52.165. б) 125 чисел. 166. а) 48 чисел. 167.40 сижобов. §4.188. б) -1.0.1,2,3.190. а) 66.193. а) 0,6; г) 5.195. а) 40 га; б) 5,4 км/ч. 199. -6.200. Частное 3, остаток 8. 201. 6)4-‘ 202. б) 14 р. 203. Иа 11%. 204. -1,5. 205. 6 мин. 207. Делимое 665, делитель 9, частное 73. 217. Например: а) р = ах’; б) р — ах + 5. 219. в) — —; г) . 222.13,8 км. 224. а) -4; 3,8; -10,4.227. г) — —. п оот 2 228. 2 км. 229.1. S5. 236. 0,2. 239. а) -9аЬ; б) 2,8лхр; д) а>5′; е) -х‘рг’. 240. 30, 24. 241. а) -6; б) -3. 243. 16 р. 244. 7. 245.1010101,-85; 1212,-50; 3210,-228; 4040,-520; 20 406, “5004; 1234„-2056; .500„= 15680.252. а); б) 0. 2.53. а) 315 см’; б) 107,2 дм’. 255. а) ; б) . 256. V =■ 6,75 дм’; S — 14,4 дм’. 2.57. 9 — 1001,, 25-11 001,, 32 — 100 000,, 75 — 1 001 011,, 100 — 1 100 100,. 267. а) 0,2; г) 0,7а; д) 2,7; е) 80; ж) 32; з) 2,55. 268. в) 0,2d 4 5; г) 0,6х. 269. б) НОД — 7, НОК — 980; в) НОД — 16. НОК — 160; 272. б) 0; в) . 27.3. 226 т. 274.37,8 т. 278.25 000 р. 279.416 р. 282. В 6-ричной с. с. 292. а) 16 и 24; б) 16 и 9.293. а) 0,9.302. б) -2,3; г) -2,5; с) 126.303. а) ; г) . 304. 25 мин 45 сек; на 20%. 307.350 и 450.308. -0,7. 309.400 м’. 310. в) -8.311, д) -0,3. 313. 30 кг, 50 кг. 314. На 1 деталь. 321. 0,72. 322. . 323. . Глава 4. S1.340. а) ; б) ; в) . 342. а) 6 м’. 346. б) ; в) . 347.5.348.180 км. 365. г) 0,585; е) 70.367. б) 1,24а; г) 2,5 с; д) 0,7х. .’468. а) 24, 20, 32. 372.360, 400, 500.374. А — 1,6: В ■= 4; а) 40%; б) 250%. 390. а) 3,6 дм. 392. а) На 56%; г) ум. на 1 %. 394. а) Ув. на 20%; б) ум. на 15%. 398. б) 49,5.399. а) -2,7.400. а) 0; в) . 402.3,6 см; 6 см; 7,4 см. 407. На 25%. 408.9720 р. 409.81. 410. а) 0; б) Q. 412.48 см’. 414. На 25%. 427. ж) 2,1 (36). 430. б) 21 м/с и 147 м. 431. 56 км. 435. 26 км/ч. 436. 1.8 км/ч. 442. 25 .м. 443. 5 мин. 445. 0,16. §2. 463. Д)р 4’^ i 12 мин. 465.Через56мин. 467,15ч. 468.6) 18ч; 14ч 24 мин. 471. д)|-^. 472.15 дн. 476. Две первые овцы. 497.6)30 мин. 498. а) 1,25; в) ^,5. 503. а) 1,9; б)-!-^. 504. а)216дп. 522. А — 60 000 акций, В -100 000 акций, С -140 000 акций. 523.2000 р., 1500 р.. 1200 р. 524. в) *20,5.527. а) ^; 75 в) -3,5р. 531. Математика — 30 мин, русский язык — 30 мин, французский язык — 45 мин, биология — 15 мин. 533. а — 7, 5 — 25; 14 и 50. S3.557. а) 7; б) 3.558. а) -10; г) -1,75.561. б) 12 км 12 м; г) 9.2 см*. 562. На 40%. .566. а)

Видео:Решение уравнений, 6 классСкачать

ГДЗ по математике 6 класс Петерсон Л.Г.

ГДЗ к учебнику Л.Г. Петерсон за 6 класс содержит решения задач по математике с детальным описанием алгоритмов и принципов поиска правильного ответа. Пособие включает в себя готовые задания для трёх частей учебника.

Автор подготовил базовый курс для шестиклассников, позволяющий получить фундамент знаний для последующего изучения алгебры и геометрии.

Решебник ускорит проверку домашних заданий и повысит уровень знаний ребенка. Решения дополняются графиками, иллюстрациями и дополнительными необходимыми материалами.

🎥 Видео

Виленкин. 6 класс за 100 минут. Математика: теория чисел, дроби, уравненияСкачать

6 класс, 42 урок, Решение уравненийСкачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Пропорция. Основное свойство пропорции. Практическая часть - решение задачи. 2 часть. 6 класс.Скачать

Математика 6 класс (Урок№51 - Решение задач с помощью уравнений. Часть 1.)Скачать

Математика 6 класс (Урок№50 - Уравнения. Часть 2.)Скачать

Пропорция. Основное свойство пропорции. Практическая часть - решение задачи. 1 часть. 6 класс.Скачать

Решение уравнений. Видеоурок 28. Математика 6 классСкачать

Пропорция. Основное свойство пропорции. 6 класс.Скачать

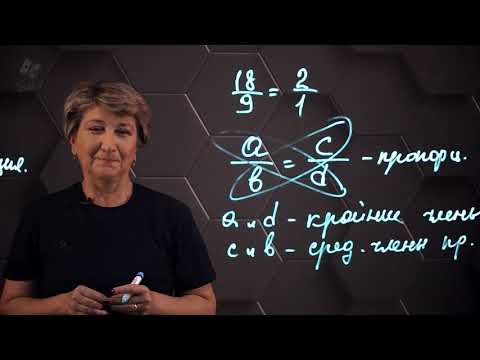
Решить уравнение - Математика - 6 классСкачать

Математика 6 класс (Урок№9 - Понятие о проценте.)Скачать

Прямо пропорциональная и обратно пропорциональная зависимость. 6 класс.Скачать

РЕШЕНИЕ УРАВНЕНИЙ ЛЕГКО ! 1 КЛАСС МАТЕМАТИКА УРАВНЕНИЯ - ПЕТЕРСОН / ОБЪЯСНЕНИЕ КАК РЕШАТЬ УРАВНЕНИЯСкачать

Решение задач с помощью уравнений. Видеоурок 29. Математика 6 классСкачать

Сложные уравнения. Как решить сложное уравнение?Скачать

Математика 6 класс (Урок№1 - Повторение материала по темам «Обыкновенные дроби» и «Смешанные дроби»)Скачать