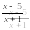Понятие рационального уравнения 8 класс никольский конспект урока (6 видео)

План конспект урока 8 класс «Понятие дробно-рационального уравнения»

Активизировать знания учащихся по теме. «Понятие дробно-рационального уравнения» Использовать их при решении задач.

Содержание

Просмотр содержимого документа «План конспект урока 8 класс «Понятие дробно-рационального уравнения»»
Понятие рационального уравнения. Решение простейших дробно-линейных уравнений.
Просмотр содержимого документа «Понятие рационального уравнения. Решение простейших дробно-линейных уравнений.»
Конспект урока на тему: «Понятие рационального уравнения»
📺 Видео

Просмотр содержимого документа
«План конспект урока 8 класс «Понятие дробно-рационального уравнения»»

Понятие дробного рационального уравнения

Содействовать развитию у учащихся мыслительных операций, анализировать, сравнивать.

Вырабатывать внимание, самостоятельность при работе на уроке. Способствовать формированию активности, максимальной работоспособности

I Организационный момент.

Проверка домашнего задания

х²=5, х²=,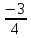

х=±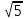. Ответ: нет корней.

Ответ: ±.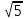

III Актуализация опорных знаний и умений учащихся:

Что такое уравнение?

Что означает решить уравнение?

Что такое уравнение?

Назовите основное свойство пропорции

IV. Объяснение нового материала.

Рациональное уравнение в котором левая и правая части являются целыми выражениями называют целым. рациональное уравнение, в котором левая и правая части являются дробными называют дробным.

Пример дробно-рационального уравнения

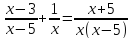
В левой части приведём к общему знаменателю, найдём область допустимых значений, данной дроби, избавимся от знаменателя дроби, получим целое уравнение: х(х-3)+х-5=х+5, после преобразования получим квадратное уравнение: х²-3х-10=0, корнями данного уравнения являются числа -2 и 5, но -5 обращает знаменатель дроби в ноль, следовательно корнем будет число -2. Выработаем алгоритм решения дробно-рациональных уравнений

1) Найти общий знаменатель дробей, входящих в уравнение;

2) умножить обе части уравнения на общий знаменатель;

3) решить полученное целое уравнение;

4) исключить из его корней те, которые обращают в нуль

5)существуют три способа чтобы избавится от знаменателя дроби:

а) умножить левую и правую часть уравнения на знаменатель,

б) приравнять знаменатели, тогда будут равными и числители,

в) воспользоваться основным свойством пропорции

V. Формирование умений и навыков.

На этом уроке отрабатывается применение алгоритма решения дробных рациональных уравнений.

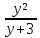
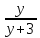
а). =Общий знаменатель (у + 3).

Умножим обе части на общий знаменатель дробей.

Можно предложить учащимся другой способ исключения посторонних корней. Как уже говорилось, при домножении обеих частей уравнения на общий знаменатель дробей, мы изменяем область допустимых значений выражений, входящих в запись уравнения. Можно тогда сперва определить ОДЗ (любые числа, кроме тех, которые обращают знаменатель в нуль), а в конце проверить, входят ли полученные корни в ОДЗ или нет.

а) 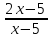– 4 = 0; ОДЗ: х + 5 ≠ 0,

в) ; ОДЗ: х # 0.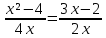

В о п р о с ы у ч а щ и м с я:

– Какое уравнение называется дробно-рациональным?

– Приведите примеры целого и дробного уравнения.

– Сформулируйте алгоритм решения дробного рационального уравнения.

– Какими способами можно исключить «посторонние» корни дробного рационального уравнения?

VII. Домашнее задание: № 600 (б, г, е), № 601 (б, е, з).

Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Понятие рационального уравнения. Решение простейших дробно-линейных уравнений.

Урок по теме арциональные уравнения.

Просмотр содержимого документа
«Понятие рационального уравнения. Решение простейших дробно-линейных уравнений.»

Конспект урока по теме «Рациональные уравнения»

знать, какое уравнение называется рациональным научиться решать рациональные уравнения;

Развивающие:
создать условия для развития мыслительных операций: наблюдения, сравнения, обобщения, конкретизации;
способствовать развитию математической речи; создать условия для развития познавательного интереса.

Воспитательные:
воспитывать навыки коммуникативности в работе, умение слушать другого, уважение к мнению товарища;
воспитывать у обучающихся такие нравственные качества, как настойчивость, аккуратность, инициативность, точность, самостоятельность, активность.

Тип урока: изучение нового материала.

Цели: создать деловой настрой для занятия; информировать о подготовке к уроку

Приветствует учащихся, отмечает их готовность к проведению урока.

2.Актуализация опорных знаний.

Цели: повторить основные понятия, необходимые на уроке, наметить шаги учебной деятельности

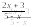
Закончите предложение:
«Дробь равна нулю тогда и только тогда, когда её числитель …
равен нулю, а знаменатель отличен от нуля.

При каких значения х данная дробь равна нулю?

Выберите правильный ответ слайд № 4

Как называются уравнения? Откуда вы их знаете? А как вы думаете, зачем ещё раз к ним вернулись? Слайд № 5

Работа с учебником: с. 94 – 95.
1) Рассмотреть пример 1.
2) Пробовать составить словесный алгоритм решения рационального уравнения. Каждому раздать.

Выполняем упражнения: 292(1 ст.), 293(1ст.)

— Какие уравнения решали?

— При решении рациональных уравнений в конце всегда надо сделать …

— Какой корень называют посторонним?

7.Подведение итогов учебной деятельности, домашнее задание.

Памятка «Правила работы в группе»

Слушай, что говорят другие

Делай выводы об услышанном, задавай вопросы

Говори спокойно, ясно, только по делу

Анализируй свою деятельность, вовремя корректируй недостатки

Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Конспект урока на тему: «Понятие рационального уравнения»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

8 класс алгебра

Дата проведения: 19.01.22г.

тема урока. Понятие рационального уравнения

Цели: ввести понятие рационального уравнения, формировать умение применять алгоритм решения рационального уравнения. Развивать математическую речь, логическое мышление, интерес к предмету. Воспитывать прилежание, трудолюбие, аккуратность, точность.

Личностные: умение контролировать, оценивать и анализировать процесс и результат учебной и математической деятельности; критичность мышления, инициатива, находчивость, активность при решении математических задач.

Предметные : знать: формулу нахождения корней квадратного уравнения; уметь вычислять квадратные корни, применять понятие и свойства квадратного корня при решении различных задач, решать квадратные уравнения с помощью формулы нахождения корней квадратного уравнения

Тип урока: формирование умений и навыков

Формы работы: фронтальная, индивидуальная

Методы и приёмы: самостоятельная, устный счёт, сравнение

Оборудование: учебник, таблица

I. Организационный момент.

II. Проверка домашнего задания.

III. Устная работа.

1. Какие из выражений являются целыми, какие – дробными?

а) ; б) (а – b) 2 – 3ab; в) ;

г) ; д) ; е) .

2. Решить уравнение: 3х 2 -4х-4=0

IV. Объяснение нового материала.

Объяснение следует проводить в н е с к о л ь к о э т а п о в.

1. В в е д е н и е п о н я т и я рационального уравнения.

Во время проведения устной работы были актуализированы следующие знания учащихся: целые выражения, дробные выражения, рациональные выражения, допустимые значения переменных. Предлагаем учащимся самим сформулировать понятие дробного рационального уравнения. Следует акцентировать их внимание на то, что наличие дроби в выражении не свидетельствует о том, что это дробное выражение (уравнение), необходимо присутствие переменной в знаменателе дроби.

2. Р а с с м о т р е н и е а л г о р и т м а решения рационального уравнения.

Рассматривая способ решения дробного рационального уравнения, учащиеся используют приём аналогии: решая целое уравнение с числом в знаменателе, они умножают обе части уравнения на общий знаменатель, что позволяет избавиться от дробей. Возникает идея применить этот приём для нового вида уравнений. После домножения обеих частей уравнения на общий знаменатель, обращаем внимание учащихся, что произошло с областью допустимых значений уравнения. Она «расширилась» и теперь допустимыми стали любые значения переменных, то есть полученное уравнение не равносильно исходному.

Вопрос: как же следует поступить в этом случае? Затем формулируется алгоритм решения дробного рационального уравнения:

1) Найти общий знаменатель дробей, входящих в уравнение;

2) умножить обе части уравнения на общий знаменатель;

3) решить полученное целое уравнение;

4) исключить из его корней те, которые обращают в нуль

V. Формирование умений и навыков.

№291 а)да; б) да; в) да; г) да; д) да; е) да; ж) нет; з) нет; и)нет; к)нет.

а)если х=2, то 3*2 — = 2+5, 6 + = 7, 6+1=7, 7=7. Ответ: является.