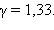Первое начало термодинамики является обобщением закона сохранения и превращения энергии для тепловых процессов. Первое начало было установлено, после того как экспериментально была доказана взаимосвязь теплоты и работы.
Первое начало термодинамики: количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами.
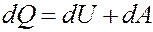
где dQ – элементарное количество теплоты, dA – элементарная работа, dU – приращение внутренней энергии.
Если dQ > 0 система получает теплоту, dQ 0 – система выполняет работу над внешними телами, dA 0, если тепловой поток направлен в сторону термодинамической системы. Величина A > 0, если система совершает положительную работу над окружающими телами.
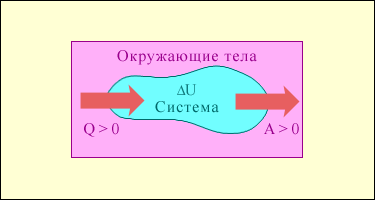 |
Рис.1. Обмен энергией между термодинамической системой и окружающими телами в результате теплообмена и совершаемой работы.
Первый закон термодинамики является обобщением опытных фактов. Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую.
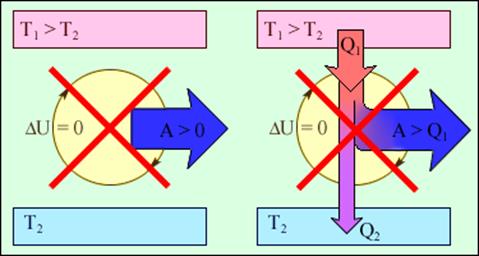
Важным следствием первого закона термодинамики является утверждение о невозможности создания машины, способной совершать полезную работу без потребления энергии извне и без каких-либо изменений внутри самой машины. Такая гипотетическая машина получила название вечного двигателя (perpetuum mobile) первого рода. Многочисленные попытки создать такую машину неизменно заканчивались провалом. Любая машина может совершать положительную работу A над внешними телами только за счет получения некоторого количества теплоты Q от окружающих тел или уменьшения ΔU своей внутренней энергии (рис.2).
Рис.2. Циклически работающие тепловые машины, запрещаемые первым законом термодинамики: 1 – вечный двигатель 1 рода, совершающий работу без потребления энергии извне; 2 – тепловая машина с коэффициентом полезного действия η > 1.
Внутренняя энергия изолированной системы постоянная величина. Для такой системы dQ = 0, dA = 0, следовательно, dU = 0 и значит U = const.
Какие бы процессы не протекали в изолированной системе, ее внутренняя энергия остается постоянной.
Если незамкнутая система выполняет круговой процесс, т.е. в результате его система возвращается в первоначальное состояние, то dU = U2—U1 = 0, следовательно, из (1) dQ = dA. То есть вся теплота, полученная системой, идет на выполнение работы. Отсюда вытекает невозможность создания вечного двигателя первого рода.
Применим I начало термодинамики к изопроцессам.
1). Изотермический процесс: T = const.
Внутренняя энергия идеального газа определяется выражением:
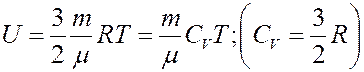
где CV – молярная теплоемкость при постоянном объеме. Определим изменение внутренней энергии.
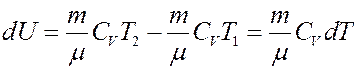
Если T = const, то dU = 0 и из I начала термодинамики получим:
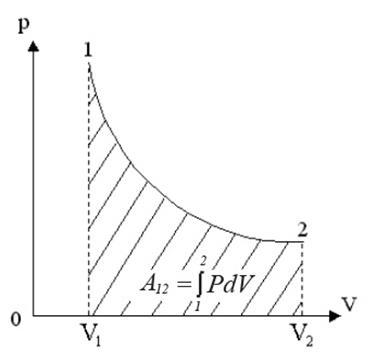
Теплота, полученная системой, идет на выполнение работы над внешними телами. Определим величину этой работы (рис.3).
Рис.3. Работа при изотермическом процессе
Элементарная работа определяется выражением:
Из уравнения Клапейрона-Менделеева:
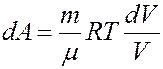
Проинтегрировав (4) найдем работу:
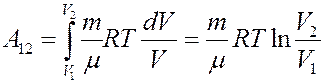
Работа численно равна площади под кривой 1 → 2. При расширении V2 > V1, и A12 > 0 система выполняет работу. При сжатии V2 V1 и A12 > 0, газ выполняет работу. При сжатии V2 T1, то Q12 > 0 газ получает тепло и его внутренняя энергия увеличивается, а если T2
| | | следующая лекция ==> | |
| Устройство пола из древесины | | | Политропический процесс. Теплоемкость. Принцип равномерного распределения энергии по степеням свободы и границы его применимости. |
Дата добавления: 2015-05-21 ; просмотров: 7537 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Применение первого начала термодинамики к изопроцессам
Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы, при которых один из основных параметров состояния сохраняется постоянным.
– Изохорный процесс (V= const). Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат (рис.11.5), где процесс 1-2есть изохорное нагревание, а 1-3— изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е.
Из первого начала термодинамикидля изохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии: δQ=dU.
Согласно формуле (11.12),
Тогда для произвольной массы газа получим
dQ=dU= 

A= 
и определяется площадью заштрихованного прямоугольника (рис.11.7).
Если использовать уравнение Клапейрона — Менделеева для выбранных нами двух состояний, то
V2–V1= ν 
Тогда выражение для работы изобарного расширения примет вид
Из этого выражения вытекает физический смысл молярной газовой постоянной R:если (Т2–Т1) = 1 К, то для 1 моль газа R=A,т. е. R численно равна работе изобарного расширения 1 моля идеального газа при нагревании его на 1 К.
В изобарном процессе при сообщении газу массой т количества теплоты
dQ= 
его внутренняя энергия возрастает на величину
dU= 
При этом газ совершит работу, определяемую выражением (11.20).
– Изотермический процесс (Т=const). Как уже указывалось, изотермический процесс описывается законом Бойля—Мариотта:
Диаграмма этого процесса (изотерма) в координатах р, V представляет собой гиперболу. Найдем работу изотермического расширения газа:

Так как при T=const внутренняя энергия идеального газа не изменяется:
dU= 
то из первого начала термодинамики (δQ=dU+δΑ)следует, что для изотермического процесса
т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:
Q = 
Следовательно, для того чтобы при расширении газа температура не понижалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.
– Адиабатический процесс.
Адиабатическим называется процесс, при котором отсутствует теплообмен (δQ=0) между системой и окружающей средой.
К адиабатическим процессам можно отнести все быстропротекающие процессы. Например, адиабатическим процессом можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько велика, что обмен энергией между волной и средой произойти не успевает. Адиабатические процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т. д. Из первого начала термодинамики для адиабатического процесса следует, что
т. е. внешняя работа совершается за счет изменения внутренней энергии системы.
Используя выражения (4.4) и (4.8), для произвольной массы газа перепишем уравнение в виде
Продифференцировав уравнение состояния для идеального газа pV=ν RT, получим
Исключим температуру Т

Разделив переменные и учитывая, что Ср/СV =γ, найдем
Интегрируя это уравнение в пределах от р1до p2 соответственно от V1до V2а затем потенцируя, придем к выражению
или p1 

Так как состояния 1 и 2выбраны произвольно, то можно записать
Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.
Для перехода к переменным Т, V p,Т исключим из (11.27) с помощью уравнения Клапейрона — Менделеева (7.9) соответственно давление или объем:
Выражения (11.27) – (11.29) представляют собой уравнения адиабатического процесса. В этих уравнениях безразмерная величина
называется показателем адиабаты. Для одноатомных газов (Ne, Не и др.), достаточно хорошо удовлетворяющих условию идеальности, i=3, γ = 1,67. Для двухатомных газов (Н2, N2, О2 и др.) i=5, γ= 1,4. Значения γ, вычисленные по формуле (11.30), хорошо подтверждаются экспериментом.
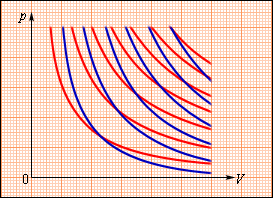
Диаграмма адиабатического процесса (адиабата) в координатах p, V изображается гиперболой (рис.11.7).

Вычислим работу, совершаемую газом в
Рис.11.7. адиабатическом процессе. Запишем уравнение (11.25) в виде
Если газ адиабатически расширяется от объема V1до V2,то его температура уменьшается от Τ1до Т2и работа расширения идеального газа
A= 
Применяя те же приемы, что и при выводе формулы (11.27), выражение (11.31) для работы при адиабатическом расширении можно преобразовать к виду
A= 
Работа, совершаемая газом при адиабатическом расширении 1–2 (определяется площадью, заштрихованной на рис.11.7, меньше, чем при изотермическом. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом – температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.
Рассмотренные изохорный, изобарный, изотермический и адиабатический процессы имеют общую особенность – они происходят при постоянной теплоемкости.
Видео:Первый закон термодинамики. 10 класс.Скачать

Пользуясь первым началом термодинамики и уравнением менделеева клапейрона обосновать закон пуассона
На рис. 3.9.1 условно изображены энергетические потоки между выделенной термодинамической системой и окружающими телами. Величина Q > 0, если тепловой поток направлен в сторону термодинамической системы. Величина A > 0, если система совершает положительную работу над окружающими телами.
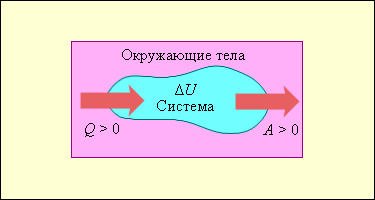 | ||||||||||||
| Рисунок 3.9.1. Если система обменивается теплом с окружающими телами и совершает работу (положительную или отрицательную), то изменяется состояние системы, т. е. изменяются ее макроскопические параметры (температура, давление, объем). Так как внутренняя энергия U однозначно определяется макроскопическими параметрами, характеризующими состояние системы, то отсюда следует, что процессы теплообмена и совершения работы сопровождаются изменением Δ U внутренней энергии системы. Первый закон термодинамики является обобщением закона сохранения и превращения энергии для термодинамической системы. Он формулируется следующим образом: Изменение Δ U внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q , переданной системе, и работой A , совершенной системой над внешними телами.
Соотношение, выражающее первый закон термодинамики, часто записывают в другой форме:
Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами. Первый закон термодинамики является обобщением опытных фактов. Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую. Важным следствием первого закона термодинамики является утверждение о невозможности создания машины, способной совершать полезную работу без потребления энергии извне и без каких-либо изменений внутри самой машины. Такая гипотетическая машина получила название вечного двигателя (perpetuum mobile) первого рода . Многочисленные попытки создать такую машину неизменно заканчивались провалом. Любая машина может совершать положительную работу A над внешними телами только за счет получения некоторого количества теплоты Q от окружающих тел или уменьшения Δ U своей внутренней энергии. Применим первый закон термодинамики к изопроцессам в газах. В изохорном процессе ( V = const) газ работы не совершает, A = 0. Следовательно,
Здесь U ( T 1) и U ( T 2) – внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит только от температуры (закон Джоуля). При изохорном нагревании тепло поглощается газом ( Q > 0), и его внутренняя энергия увеличивается. При охлаждении тепло отдается внешним телам ( Q изобарном процессе ( p = const) работа, совершаемая газом, выражается соотношением
Первый закон термодинамики для изобарного процесса дает:
При изобарном расширении Q > 0 – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии Q A T 2 T 1; внутренняя энергия убывает, Δ U изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, Δ U = 0. Первый закон термодинамики для изотермического процесса выражается соотношением Количество теплоты Q , полученной газом в процессе изотермического расширения, превращается в работу над внешними телами. При изотермическом сжатии работа внешних сил, произведенная над газом, превращается в тепло, которое передается окружающим телам. Наряду с изохорным, изобарным и изотермическим процессами в термодинамике часто рассматриваются процессы, протекающие в отсутствие теплообмена с окружающими телами. Сосуды с теплонепроницаемыми стенками называются адиабатическими оболочками , а процессы расширения или сжатия газа в таких сосудах называются адиабатическими . В адиабатическом процессе Q = 0; поэтому первый закон термодинамики принимает вид
т. е. газ совершает работу за счет убыли его внутренней энергии. На плоскости ( p , V ) процесс адиабатического расширения (или сжатия) газа изображается кривой, которая называется адиабатой . При адиабатическом расширении газ совершает положительную работу ( A > 0); поэтому его внутренняя энергия уменьшается (Δ U | ||||||||||||
| Рисунок 3.9.2. В термодинамике выводится уравнение адиабатического процесса для идеального газа. В координатах ( p , V ) это уравнение имеет вид
Это соотношение называют уравнением Пуассона . Здесь γ = C p / C V – показатель адиабаты, C p и C V – теплоемкости газа в процессах с постоянным давлением и с постоянным объемом (см. §3.10). Для одноатомного газа Работа газа в адиабатическом процессе просто выражается через температуры T 1 и T 2 начального и конечного состояний:
Адиабатический процесс также можно отнести к изопроцессам. В термодинамике важную роль играет физическая величина, которая называется энтропией (см. §3.12). Изменение энтропии в каком-либо квазистатическом процессе равно приведенному теплу Δ Q / T , полученному системой. Поскольку на любом участке адиабатического процесса Δ Q = 0, энтропия в этом процессе остается неизменной. Адиабатический процесс (так же, как и другие изопроцессы) является процессом квазистатическим. Все промежуточные состояния газа в этом процессе близки к состояниям термодинамического равновесия (см. §3.3). Любая точка на адиабате описывает равновесное состояние. Не всякий процесс, проведенный в адиабатической оболочке, т. е. без теплообмена с окружающими телами, удовлетворяет этому условию. Примером неквазистатического процесса, в котором промежуточные состояния неравновесны, может служить расширение газа в пустоту . На рис. 3.9.3 изображена жесткая адиабатическая оболочка, состоящая из двух сообщающихся сосудов, разделенных вентилем K . В первоначальном состоянии газ заполняет один из сосудов, а в другом сосуде – вакуум. После открытия вентиля газ расширяется, заполняет оба сосуда, и устанавливается новое равновесное состояние. В этом процессе Q = 0, т.к. нет теплообмена с окружающими телами, и A = 0, т.к. оболочка недеформируема. Из первого закона термодинамики следует: Δ U = 0, т. е. внутренняя энергия газа осталась неизменной. Так как внутренняя энергия идеального газа зависит только от температуры, температура газа в начальном и конечном состояниях одинакова – точки на плоскости ( p , V ), изображающие эти состояния, лежат на одной изотерме . Все промежуточные состояния газа неравновесны и их нельзя изобразить на диаграмме. Расширение газа в пустоту – пример необратимого процесса . Его нельзя провести в противоположном направлении. 📸 ВидеоАдиабатный процесс. 10 класс.Скачать  Обратимые и необратимые процессы. Энтропия. Второй закон термодинамики. 10 класс.Скачать  Физика 10 класс (Урок№24 - Первый закон термодинамики.)Скачать  Первый закон термодинамики | Физика 10 класс #41 | ИнфоурокСкачать  Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать  Применение первого закона термодинамики к изопроцессам. 10 класс.Скачать  Физика 10 класс: Уравнение Клапейрона-МенделееваСкачать  Законы Термодинамики. Что Такое Термодинамика?Скачать  Уравнение Менделеева - Клапейрона за 10 минут | Физика с Никитой АрхиповымСкачать  Применение первого начала термодинамики к изопроцессамСкачать  Урок 170. Количество теплоты. Первый закон термодинамикиСкачать  Что такое первый закон термодинамики?Скачать  ВСЯ МКТ И ТЕРМОДИНАМИКА ЗА 6 ЧАСОВ С НУЛЯ I Физика ОГЭ ЕГЭ 2024 I Эмиль Исмаилов I Global_EEСкачать  Первый закон термодинамикиСкачать  ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ просто | Физика ЕГЭ 10 класс УмскулСкачать  Лекция №2 "Второе начало термодинамики"Скачать  ФИЗИКА ЗА 5 МИНУТ - ТЕРМОДИНАМИКАСкачать  Физика. Термодинамика: Адиабатный процесс. Центр онлайн-обучения «Фоксфорд»Скачать  |
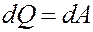
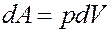
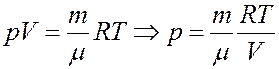
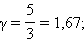 для двухатомного
для двухатомного 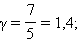 для многоатомного
для многоатомного