Получить дискретную передаточную функцию и разностное уравнение пид регулятора

ПИД-регулятор является простейшим регулятором, имеющим эффективные аппаратные аналоговые реализации, и потому применяемый наиболее широко. Для своей работы требует настройки 3х коэффициентов под конкретный объект, позволяющие подобрать процесс регулирования согласно требованиям. Обладая простым физическим смыслом и простой математической записью, применяется широко и часто в регуляторах температуры, регуляторах расхода газа и других системах, где требуется поддерживать некий параметр на заданном уровне, с возможными переходами между разными заданными уровнями. Разумеется, существуют более сложные регуляторы, позволяющие более точно и быстро и с меньшими перерегулированиями выходить на заданные параметры, а так же учитывающие нелинейность или гистерезис регулируемого объекта, однако они обладают большей вычислительной сложностью и сложнее в настройке.

Несмотря на свою простоту как физического смысла, так и математической записи: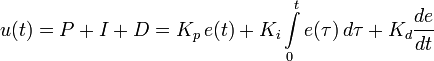

при програмной реализаци ПИД регулятора очень часто допускают ошибки, которые встречаются даже в поверенных приборах автоматики.

Причем проверить качество реализации ПИД регулятора крайне легко.

Рассмотрим простейший пример: терморегулятор. Для проверки его качестве лучше всего подходит быстрый, малоинерциальный, маломощный объект. Классика жанра: обычная лампочка на 100Вт с прикрученной к ней тонкой термопарой (ХА). И первое, на чем следует проверять ПИД регулятор — деградация ПИД до просто П-регулятора. То есть коэффициенты интегральной и дифференциальной ставим в ноль, а пропорциональную ставим в максимум.

Включаем регулятор, проверяем: текущая температура 22 градуса, уставка 16 градусов. Лампочка не горит. Начинаем начинаем увеличивать уставку: 16.1, 16.3, 16.7, 18… 19… лампочка загорелась. Как?! Откуда?! Останавливаемся — выключилась. Итак, мы встретились с первой классической ошибкой реализации ПИД регулятора.

Небольшое математическое отступление: вспомним еще раз интегральную запись указанную выше. Мы реализуем её програмно, а значит — дискретно. То есть с завидной регулярностью производим измерение входной величины, сравниваем её с уставкой, вычисляем воздействие, выдаём, повторить. А значит, надо из интегральной формы перейти в конечно-разностную схему. При переходе обычно используется переход «в лоб»: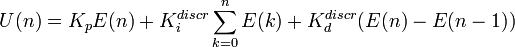

где E(n) = X(n) — X0(n) — то есть величина рассогласования между текущим и заданным значением регулируемого параметра.

Использование прямой формулы потребует во-1х считать и хранить интеграл рассогласований за большой период, во-2х требует работы с плавающей точкой высокой точности (так как интегральный коэффициент Ki всегда U(n) по вышестоящей формуле, добавляется еще ограничение результата:
if Un Umax then Un := Umax;
После чего, вычисленное Un и есть требуемая выходная мощность на текущий момент. Та-дам! Именно вот эта реализация и создаёт ошибку, о которой написано выше.

Причина банальна: в момент перехода от дикретной к конечно-разностной схеме, мы «выносим за скобки» операцию вычисления интеграла, и на каждом шаге мы прибавляем производную к накопленной сумме U(n-1) . Наложив же на неё ограничение, мы весь вычисленный интеграл фактически обнуляем. (Ну не сколько обнуляем, сколько приводим к диапазону 0-100, что в данном случае несущественно). Таким образом, мы дифференциурем ПИД регулятор, и остаётся дифференциально-ускорительный. Что в реальности выглядит как просто дифференциальный регулятор — мощность при этом подаётся пропорционально изменению уставки или регулируемой величины, а не пропорционально разности между уставкой и регулируемой величиной.

Вывод №1: вычисление U(n) нельзя ограничивать. Для ограничения мощности подаваемой на выходное устройство следует заводить отдельную переменную.

Теперь, когда мы завели Urn, для ограниченной мощности, перезаливаем, продолжаем тестировать.
Включаем регулятор, проверяем: текущая температура 22 градуса, уставка 16 градусов. Лампочка не горит.
Начинаем прибавлять уставку: 16.1, 16.4, 17, 18, 20, 22, 24 (опа! засветилось! ура!), 28, 30, 40, 60… Красота! Работает!
Наблюдаем за процессом — вышло примерно на 60, болтается чуток туда-сюда, но держит. Вроде, всё красиво. Выдыхаем, проверяем управление с ПК: задаём 600 градусов. И… Лампочка выключается. Как так? Уставка 600, текущая 60, а лампочка не горит?

Пока ждём и медленно осознаём, что мы явно напоролись на какой-то «Классический Косяк №2» ™ лампочка медленно разгорается, выходит на 100% мощности, и так и остаётся — 600-то градусов она выдать ну никак не может.

Возвращаемся снова к нашей разностной схеме. U(n) = U(n-1) + Kp*(dE + . ) . К текущему расчетному значению воздействия прибавляется разность невязки помноженная на коэффициент пропорциональности. У нас была уставка 60, температура 60, то есть невязка нулевая. Выходная мощность так же была нулевая. И тут разом, скачком, уставку увеличили до 600 градусов. невязка резко стала 540 градусов, помножили еще и на коэффициент пропорциональности… и вылетели за разрядность хранения U(n). Не смейтесь, использование математики с фиксированной точки, вместо плавающей точки. При разнице в 540 градусов и работе через 1/16, при коэффициенте пропорциональности 20, получаем… 540*20*16=172800, а если у нас 16тиразрядный U(n), да еще и знаковый, то фактически, в результате вычисления мы получили A300h = −8960. Опачки. Вместо большого плюса — ощутимый такой минус.

Вывод №2: вычисления должны проводиться с корректной поддержкой переполнения. Переполнилось? Ограничь предельным числом, уж никак не заворачивать.

Итак, нарастили разрядность U(n), перетранслировали, зашили, запускаем. Лампочка еще не совсем остыла, там 80 градусов, уставка всё те же 600. Лампочка зажигается… и тухнет. Зажигается и тухнет. Как так? Уставка 600, лампочка 80 — и поддерживает вполне себе свои 80! Как так-то?! Явно у нас вылез Жучок №3.

И снова лирически-математическое отступление. Итак, есть наша разностная схема: U(n) = G(U(n-1), dE(n)) . Еще раз: новое значение воздействия есть сумма прошлого воздействия и некого воздействия, зависящего от разности невязки в текущий момент и предыдущий. А что такое предыдущий момент? А какой момент предыдущий у предыдущего? Ну-ка, вспомнили школу. Доказательство по индукции. Если можно построить доказательство для K+1, считая что доказательство для K верно, И доказать отдельно что верно для K=0, тогда доказательство истинно. Итак, а как мы считаем U(0)?

Часто встречающееся решение: всё обнуляем, уставку считываем из флешпамяи уставки, ждём 1 цикл опроса, и считываем X(0). Вот, ноль готов, теперь работаем. И… И не правильно. Почему? Потому что рекурентная формула отталкивается от изменений в невязке. А проинициализировав нулём и загрузив текущие значения мы потеряли стартовые условия. Всё — вместо поддержания абсолютного значения температуры на уровне равном абсолютной уставке регулятор начинает держать температуру равную стартовой плюс разнице уставки. То есть было 80 градусов и уставка 200, включили прибор — он держет 80. Сменили уставку на 240 — он начал держать 120.

Правильная инициализация разностной схемы: обнулить _вообще всё_. То есть
X(0) = 0, X0(0) = 0. U(0) = 0. E(0)=X(0)-X0(0)=0.
И на первом же цикле вычислений у нас как бы скачком появляются уставке и текущее значение:
X(1) = 80. X0(1)=200. U(1) = U(0)+Kp*(E(1)-E(0)) = U(0)+Kp*(X(1)-X0(1)-E(0)) = 0 + 20*(200 — 80 — 0) = 2400
Вот теперь схема работает правильно.

Вывод №3: корректно инициализируй стартовые условия.

Правильно ли? Hу-ка, ну-ка… Еще раз… Ставим уставку 20. Ждём охлаждения… Выключаем. Включаем. Итак, красота: текущая 20, уставка 20. Ставим скачком 600. Поехало греться. 100, 120… ставим уставку 20. Отключилось, пошло охлаждаться. Ждём чуток (120… 110… 100… 90… 80. ) и ставим уставку 100. Поехало греться… 105 градусов, отключилось. Стоп. А почему оно держит 105? У нас же сейчас работает только пропорциональная составляющая. При правильной реализации из физического смысла процесса колебательный процесс не может держать уставку выше чем задано. Строго ниже. А держит на 5 градусов больше чем попросили. Это наблюдается Прикол №4.

Итак, вспоминаем что у нас было выше: Вывод№2: U(n) нельзя ограничивать. И Вывод№3: при переполнении ограничить всё-таки придётся. Да-да. Иначе «рабочая точка» смещается на ограниченный момент. Что же делать? Увеличить разрядость? Хорошо, если хватает вычислительной мощности. А надо ли? Собственно, что плохого, что у нас U(n) = 9999.99, а не 29999.99? В общем-то только то, что мы потеряли 20000. Но сейчас-то для работы нам так и так надо вваливать просто 100% мощности, правильно? Правильно. Значит, проблемы с ограничением в полку нет, до тех пор, пока мы не отходим от предела. Таким образом, в случае переполнения надо ставить флаг, и по достижении, например, половины диапазона (то есть как U(n) после 9999.9 опустилось ниже 5000.00), заново реинициализировать схему. То есть отбрасывать историю, сказать что n=0 и см. выше Вывод №3. Пытливый ум уже сообразил, что в случае полной схемы, когда все три компоненты не равны нулю, обнуляя в процессе итеративный процесс, мы в том числе обнуляем накопленный интеграл интегральной составляющей. Однако, в связи с тем, что обнуляем мы значительно заранее, он успеет подкопиться за время довырабатывания остатка. Да и не совсем корректно копить интеграл на «больших» перегонах, так как цель интегральной составляющей — «выбрать» невязку, которую не может отработать пропорциональная составляющая отдельно.

Вывод №4: если по какой-то причине U(n) было ограничено, схему следует переинициализировать как только создалось впечатление, что схема вернулась в нормальное состояние.

В следующем выпуске: а так ли надо реализовывать разностную схему? Подробная реализация прямой дискретной схемы, обладающей простыми и понятными настраиваемыми коэффициентами, с прямым физическим смыслом, которая без проблем вычисляет управляющее воздействие с частотой 25Гц на процессоре ADuC847 (быстрый 8-битный контроллер, с ядром 8051), оставляя еще море процессорного времени для других процессов.

(Картинки с изображением формул взяты из статьи ПИД-Регулятор в Wikipedia)

Видео:Теория автоматического управления. Лекция 2. Дискретные САУ. Решетчатые функцииСкачать

ПИД-регуляторы – для чайников-практиков

Обещал я недавно моему знакомому — хорошему электрику и чайнику в электронике — сделать небольшое устройство в автомобиль, которое, регулируя заслонку, будет поддерживать обороты в дОлжном состоянии (все подробности по авто-части к нему. Знаю, что назвали мы эту чучу умным словом «регулятор холостого хода»). Причем эти обороты должны зависеть от текущей температуры двигателя. «Так тебе нужно работать с ПИД-регулятором» — сказал я ему. А в ответ увидел туман в глазах, дым в ушах и дрожащий голос – «А это ничего общего со СПИДом не имеет. ». В общем, придется ему объяснить подробности, при этом избегая математики. В Интернете море статей на эту тему (достаточно начать отсюда). Моя статья – еще одна ложка в море информации. Интересующимся – под кат!

Что мы делаем?

Итак, мы делаем регулятор холостого хода.
В данном случае однозначно просится к реализации система управления с обратной связью. В своей статье про «Датчики и АЦП» я рассказывал про систему управления с обратной связью, подробности ищите там. Также там была неплохая картинка на эту тему:

Что это будет в данном случае?
Мы хотим управлять оборотами двигателя в состоянии холостого хода. Для этого у нас есть шаговый двигатель, который открывает/закрывает заслонку для регулировки подачи воздуха. Также у нас есть таблица, которая указывает желаемую частоту двигателя в зависимости от текущей температуры. Управление объектом тут у нас выполняется шаговым двигателем. Состояние объекта определяется 1) оборотами двигателя и 2) текущей температурой.
Для данной картинки получаем следующее:

• Объект — двигатель автомобиля;
• Измерение производится для 1) оборотов двигателя (в нашем случае – промежуток времени между соседними импульсами тахометра, которых два на один оборот) и 2) температуры двигателя (сопротивление терморезистора);
• Воздействие направлено на обороты двигателя, для чего регулируется заслонка воздуха. Регулируется она шаговым двигателем. Значит, мы задаем степень смещения для шагового двигателя;
• Расчет — вычисление требуемого смещения в зависимости от 1) оборотов двигателя, 2) температуры двигателя, 3) текущего состояния шагового двигателя;
• Общение в данном случае отсутствует (впрочем, я выведу наружу COM-порт для настройки/диагностики устройства).

Итак, мы измерили все, что надо, и получили Обороты (t) — текущие обороты двигателя (текущего момента времени t), Температуру (t) — текущую температуру. Также у нас есть Шаг (t) — текущий шаг заслонки и Обороты (t+1) — новое значение оборотов двигателя, которое зависит от температуры. Получить нам в итоге надо Шаг (t+1) — новое положение заслонки.
Немного математики:

Что это за функция? Она выдает нам текущее значение шага, которое зависит от всего вышеперечисленного. Как она это делает?
Вся собака зарылась в том, что мы хотели на данный шаг получить одни обороты, а они в реальности совсем другие! Значит, нам нужно знать значение текущей ошибки (невязки), и она может быть вычислена как разность предполагаемых оборотов в будущем и текущих:

Ошибка (t) = Обороты (t+1) — Обороты (t).

В случае, когда обороты четко соответствуют требуемому значению (к чему мы и стремимся), ошибка будет равна нулю. Эта ошибка нам показывает насколько сильным должно быть воздействие.
Формула для следующего шага теперь может быть записана следующим образом:

Теперь можно вынести значение предыдущего шага за скобки:

Все понятно? Мы на каждом шаге работы регулятора должны задавать текущее положение шагового двигателя. Он зависит, понятное дело, от предыдущего шага и от ошибки. Шаговый двигатель управляется смещениями, поэтому нам не так уж и важен текущий шаг (проигнорируем тему выхода за пределы допустимого количества шагов – моему другу электрику это знать не обязательно). В итоге можно перейти к такой записи:

ИзменениеШага (t+1) = Функция .

Во как все упростилось! В итоге мы пришли к загадочной функции, которая зависит от текущей ошибки. Что это за функция? Думаю, все уже догадались – это пропорционально-интегрально-дифференциальный регулятор.
Справедливости ради надо указать темы, которые мы проигнорировали (опять же – эти тонкости не для электриков!):

• дискретностьtили размер шага. С какой частотой мы делаем воздействие? Я не знаю – я еще только разрабатываю сие чудо техники. Думаю, что шага в 50 мсек хватит за глаза. В моей программе это будет настраиваемый из EEPROM параметр. Впрочем, эту тему игнорировать нельзя и мы к ней еще вернемся;
• управление шаговым двигателем. Там своя масса нюансов. Читайте Интернет, googl-ите – тема широко освещена;
• связь функции с шагом и оборотами. Ошибку-то мы вычислили, ее размерность совпадает с размерностью оборотов двигателя (в моем случае это время, мсек). Как она преобразуется в размерность шага? Эту тему мы тоже оставим за бортом, т. к. это не имеет отношения к теме, собственно, ПИД-регуляторов. Для особо любопытных – я буду брать % от максимально возможной ошибки (задается максимально/минимально допустимыми оборотами) и пропорционально его превращать в % от максимально возможного одиночного изменения шага (задается полным диапазоном шагов двигателя).

Формула ПИД-регулятора

Как я и обещал, формул тут не будет… ну, почти не будет. И этот раздел – как раз и будет формулой. Обещаю – больше формул не будет! Так что потерпите!
Итак, формула ПИД-регулятора:

(навеяно Википедией)
Тут у нас следующие буковки (разъясним чуть ниже):

• u (t) — наша Функция;
• P — пропорциональная составляющая;
• I — интегральная составляющая;
• D — дифференциальная составляющая;
• e (t) – текущая ошибка;
• Kp — пропорциональный коэффициент;
• Ki — интегральный коэффициент;
• Kd — дифференциальный коэффициент;

Все, расслабились – больше эта формула нам в работе не понадобится, она для пояснения сути.
А суть тут такая.
У нас есть воздействие, наша Функция (u (t) ). Она состоит из трех составляющих – Пропорциональной, Интегральной и Дифференциальной (отсюда и ПИД-регулятор).
Формула в вышеприведенном виде хороша для изучения, но неудобна для расчетов (хотя бы потому, что в вычислительной технике надо переходить к численным методам). В программной реализации, если верить этой статье, переходят к дискретной реализации:

Вот это уже выглядит куда реальнее и понятнее! Мы вычисляем сумму трех составляющих. Каждая из них определяется своими коэффициентами. Если данный коэффициент нулевой, то составляющая в вычислении не участвует. С этой формулой мы и будем работать далее, ее я и реализую.
Впрочем, есть еще и другая, рекуррентная реализация:

Какая из них лучше/правильней? Математика, в общем-то, одинаковая. Коэффициенты тоже. Говорят, что есть разные подводные булыжники при реализации.
Обратите внимание! Коэффициенты тут – обязательно дробные числа! В языке программирования Си – как минимум float, а лучше бы и double.
Вся магия ПИД-регуляторов – именно в этих коэффициентах. Как их подбирать – посмотрим в конце. А сейчас переведем дух от математики и поедем к изучению поведения этой формулы.
Все расчеты и моделирование я проводил на модели в Excel. Он – файл – приложен внизу, с ним можно поиграться самостоятельно. Модель – сугубо для ознакомления с идеей! Т. е. не надо ее стараться привести к какому-то реальному процессу, искать в ней научный смысл и т. п. Там все цифры слегка «отфонарные». Но зато и файл простенький и несложный. И моделируется быстро. И дает возможность понять суть ПИД-регулятора. Пару слов по файлу я дам в конце.

Пропорциональная составляющая

Первый коэффициент – пропорциональный. Он самый очевидный и понятный (реально я когда-то давно сам вывел формулу ПИД-регулятора, кому-то показал, и он рассказал мне об этой теории; так вот, вывод я начал с пропорционального вида).
Рассмотрим его – пропорционального коэффициента — влияние на результат.

«Ожидаемое» – это то, что мы хотим получить. Вначале оно равно какому-то низкому значению (в нашем примере – это те обороты двигателя, которые создает стартер). Далее, в момент времени 3, оно вдруг стало равно 2000 (завели мотор и, исходя из текущей температуры, мы должны получить 2000 оборотов в минуту).
(Небольшая ремарка – в автомобилях частоту измеряют в кол-во оборотов в минуту!)
Сделаем первый вариант: Kp = 2. Посмотрим на красную линию. Что мы видим? По ходу дела обороты начали расти – ошибка стала снижаться – значение коррекции постепенно растет — красная линия растет (обороты двигателя увеличиваются). В какой-то момент (почему-то 13-ый) обороты достигают требуемой величины. Класс? Супер! Да вот только медленно как-то…
Попробуем другой коэффициент: Kp = 5. Что видим? Зеленая линия. Достигла результата шустро – на 6-ом шаге. Класс! Да вот – ой! – перелет (по науке перерегулирование). Потом, правда, вернулись назад – порядок.
А что если коэффициент сделать еще больше? Kp = 20. Синяя линия – бух! За один шаг! Но – сразу перелет. Потом падаем вниз – ошибка стала отрицательной. Опять сильно вниз! Рывок вверх! Опять вниз! Что видим? Пошли колебания. Они, слава Богу, затухающие.
Если увеличивать коэффициент больше, то такие колебания могут стать незатухающими. Система начнет колебаться все больше и больше, пока не … ну-у, тут уже все зависит от конкретной системы.
Какова природа колебаний? Система, на которую воздействуют, всегда (в реальной жизни) инерционна. Обороты повышаются – коэффициент падает к нулю. И вот – достигли нужной точки. Коэффициент ошибки (и регулирования) достиг нуля. Но ведь процесс поднятия оборотов инерционен! Движёк раскочегарен, обороты продолжают по инерции расти. И тогда будем двигать заслону назад – опускать обороты. Опять достигли нуля – а обороты продолжают падать… И так, в общем-то, до бесконечности.
Особенно это очевидно в системах поддержания температуры. Нагрев надо выключать до нужной температуры – чтобы сам нагреватель перестал разогреваться и греть объект.
Для решения этой проблемы используется следующая –

Интегральная составляющая

Эта составляющая накапливает ошибку (как и любой интегратор). Т. е. постепенно накапливается эта самая ошибка, интегратор «наполняется» и его воздействие увеличивается. Эффект от такого накопления не мгновенен — ибо ошибка должна накопиться, на что уходит некоторое количество шагов алгоритма.
Рассмотрим случай, когда Kp = 5, а Ki будем менять:

Вариант 1 (красный) – Ki = 0.
Вариант 2 (зеленый) – Ki = 0.2.
Вариант 3 (синий) – Ki = -0.3.
Использование положительного коэффициента (зеленая линия) в данном случае, пожалуй, ничего нам не дало. А вот отрицательный коэффициент (синяя линия) очень даже неплохо помог! Но вот только линяя пошла вниз, и потом она приведет к раскачиванию системы… (но на практике раскачивания системы, как правило, не происходит, т. к. постоянно будут коррекции текущего состояния)
Итак, интегральная составляющая позволила нам сгладить резкий эффект пропорциональной составляющей. Это неплохо!
Но вы погодите – сейчас нам покажет всю свою мощь

Дифференциальная составляющая

Эта составляющая пропорциональна темпу изменений. Как подсказали в комментариях, она «придает ускорение».
Как и ранее, Kp = 5, а Kd будем менять:

Вариант 1 (красный) – Kd = 0.
Вариант 2 (зеленый) – Kd = 0.2.
Вариант 3 (синий) – Kd = -0.2.
Каково? И сглаживает, и не дает раскачиваться в будущем!

Реакция на помехи

Надо еще не забывать об одной такой малоприятной вещи – о помехах. Они будут раскачивать лодку нашей системы.
Вот картинка, когда у нас стоит задача поддерживать одно и то же значение оборотов:

Шумовое (случайное) воздействие – одинаковое для всех вариантов.
Вариант 1 (красный) – Kp = 10, Ki = 0, Kd = 10.
Вариант 2 (зеленый) – Kp = 10, Ki = 2, Kd = 0.
Вариант 3 (синий) – Kp = 10, Ki = 2, Kd = 6.
Как видно, с добавлением составляющих стабильность (немного) увеличивается.

Настройка

Я думаю, общее представление о формуле ПИД-регулирования вы получили. Программируется легко, эффект красивый. И следующий вопрос у вас будет – «а как получит коэффициенты»? И вот тут все становится кисло… Потому что, если до этих пор шла строгая математика, то дальше начинаются танцы с бубнами, шаманство и шайтанство. Нет, все-таки есть какие-то точные методы, но мне становится плохо при мысли, что я должен это проделать для своего двигателя в автомобиле!
В комментариях мой метод (и мое понимание) настройки разгромили, закопали и затоптали. И порекомендовали прочитать хорошую книгу «ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ДЛЯ «ЧАЙНИКОВ»» К.Ю. Полякова (созвучное название, не находите?). Согласен, тема (настройки) сложная, для меня неоднозначная, поэтому соглашусь с комментирующими — надо прочитать эту книгу и глубже вникать в тему. Но… это уже будет не для уровня чайников, не так ли? В книге Полякова формул более чем достаточно, а это уже уровень электро-чайника! Так что позвольте мне изложить свой подход. Неидеальный, но достаточный для старта и более детального изучения темы.

Прежде всего, вы должны иметь четкое представление о своей системе регулирования – насколько она инерционна? какие шумы на нее могут воздействовать? какие воздействия (результаты функции ПИД-регулятора) для нее недопустимы?
Следующий вопрос – насколько вашу систему можно погонять туды-сюды? Все методы, что я нашел, базируются на тестовых воздействиях на систему и анализе результатов. Нужно пробовать, пробовать, считать, считать, считать (ну или по науке — строить модель)… А температура двигателя-то растет, и воздействие через полчаса работы уже будет совсем не таким, как при начале. А как вы в один и тот же день проверите работу при -30оС и +30оС.
Вот несколько полезных советов оттуда же:

• увеличение пропорционального коэффициента увеличивает быстродействие и снижает запас устойчивости;
• с уменьшением интегральной составляющей ошибка регулирования с течением времени уменьшается быстрее;
• уменьшение постоянной интегрирования уменьшает запас устойчивости;
• увеличение дифференциальной составляющей увеличивает запас устойчивости и быстродействие.

Впрочем, несколько обнадеживает информация из другой статьи: «ПИД-регуляторы замечательны тем, что для их хорошей настройки не требуется отличного понимания формальной теории управления системами. При этом они позволяют решить около 90% всех задач управления простыми системами замкнутого цикла.»
Там же описана процедура настройки. Рекомендую почитать — просто и со вкусом.
Мой же подход базируется на следующем.

Частота опроса/воздействия

Есть очень важный момент работы при разработке ПИД-регулятора: воздействие должно быть строго периодичным, т. е. производиться через равные промежутки времени! Аналогично, ошибка должна вычисляться также периодически.
Какой должен быть период измерений/воздействий? Для начала определите время стабилизации системы – за сколько должно быть достигнуто устойчивое состояние (в случае регулятора холостого хода хватит периода 0.5 секунды). Потом разделите это время на 10 … 100 – и вы получите длительность шага (в моем случае хватит и 10 мсек). А вообще – чем выше частота, тем лучше! Но надо помнить, что операции с дробными числами весьма медленны. Фактически, они и зададут вам период работы.
Посмотрим, как период опроса (и воздействия) влияет на качество результата:

Коэффициенты ПИД-регулятора: – Kp = 10, Ki = 0, Kd = 0.
Вариант 1 (красный) – период опроса 0.5 у.е.
Вариант 2 (зеленый) – период опроса 0.35 у.е.
Вариант 3 (синий) – период опроса 0.15 у.е.
Как видим, в первом случае есть мощные выбросы. Во втором случае (70% от первого периода) они стали слабее, а в третьем (30%) – преобразование вообще получилось гладким! Т. е. для первых двух вариантов нужны дополнительно интегральная или дифференциальная составляющие, а для последнего мы обошлись только пропорциональной. А это существенная разница в вычислениях!
Так что вопросу выбора периода надо уделить первостепенное внимание.
Итак, время выбрали, все коэффициенты сбросили в ноль. Начинаем управлять системой.
Идеально, если вы сможете собрать статистику – записывать воздействие/результат/сопутствующую информацию в текстовый файл. Потом его можно открыть в том же Excel и проанализировать.

Настройка пропорционального коэффициента Kp

Для начала я устанавливаю коэффициент Kp в 1 и смотрю, что будет. Растет слишком медленно – увеличиваю. В какой-то момент начнутся перелеты и колебания. Значит, многовато – уменьшаем. Исчезли – немного увеличиваем. Начались – немного уменьшаем. Исчезли — … И так далее, пока не надоест. В итоге получили достаточно устойчивый пропорциональный регулятор, который надо немного скорректировать (надо ли? Если все работает вполне качественно, то не морочим себе голову и считаем, что все настроено)

Настройка дифференциального коэффициента Kd

Понемногу наращиваю коэффициент Kd — 0.5, 1,… Колебания системы уменьшаются, все работает красивее… Пока не происходит обратное – начинаются мощные выбросы. Все, перерегулировали, уменьшаем.
Итак, имеем выбросы – уже меньше, но все равно имеем. Самое то сгладить, притормозить воздействие!

Настройка интегрально го коэффициента Ki

Шаманим дальше. Берем совсем немного – 0.1 для начала. Можно попробовать и небольшое отрицательное значение. Смотрим, пробуем, крутим…
Процесс этот – настройки – итерационный. Стоит пробовать разные варианты, начинать сначала. Для меня он по-прежнему туманен и шайтанен.

Дополнительные модули?

Построили, сделали — и увидели, что все равно есть какие-то биения, ненужные колебания. Ну-с, а что вы хотели. Серьезный подход изобилует формулами, сложными расчетами!
И Бог с ними — вот что я скажу! Можно вполне на выходе добавить усреднение нескольких последних тактов — дешево (в плане расчетов) и сердито (в плане стабильности воздействий). Можно поставить еще какие-нибудь фильтры.
Не будем догматичными! Кто сказал, что нужно ограничиться одним лишь ПИД-регулятором?

Информация по модели

А теперь – обещанная пара слов по Excel-файлу. В нем реализована модель, схожая с перемещением по линии. Не очень корректная, возможно, но вполне достаточная для старта (может, по результатам обсуждения сделаю более точную модель — возьму для примера модель электродвигателя из статьи Полякова). Есть предыдущее положение, скорость и ускорение. Скорость рассчитывается как разница предыдущих перемещений. Ускорение определяется как П-И-Д – воздействие, умноженное на коэффициент усиления (в верхней части таблицы).
В таблице представлены 3 варианта. Они настраиваются сверху:

• Коэффициент усиления задает множитель для ускорения. Меньше единицы – воздействие будет «тормозить», больше – раскачивать систему;
• Начальное значение — стартовое значение оборотов двигателя;
• Шаг времени используется в формуле расчета новых значений. Его увеличение «ускоряет» моделирование (и исчезают все мелкие шаги);
• Шум — диапазон изменения случайного числа. Ставите 0 – и его воздействие на моделирование исчезает;
• Воздействие — три коэффициента для расчета. Меняете, смотрите;
• Колонка желаемое — то значение, к которому стремится ПИД-регулятор. Его можно менять в любой клетке по высоте. Там сейчас заложено несколько ступенек

Результат моделирования – 2 графика. Первый – маленький – показывает несколько значений вначале. Второй показывает всю таблицу.
Попробуйте поменять в этом файле коэффициенты – результат будет сразу виден. По ходу дела вы сами заметите закономерности, о которых тут написано (и выведете свои новые).

В заключение – о реализации

С теорией вроде бы разобрались. Теперь – о реализации.
Сердце регулятора – формула. Она оперирует с дробными числами. Учтите, что такие операции и на 32-хбитным контроллерах выполняются не моментально, что тут говорить о 8-битках! Вычисление отдельных частей формулы – П-, И-, Д- — лучше написать не одной строкой на Cи, а разбить на части. И делать между ними что-нибудь полезное.
(ну… все не так трагично. У меня на ATMega в Cv AVR2 с 8 МГц кварцем формула просчиталась за 0.18мсек. Для моих нужд — с головой!)
И еще не забываем ограничивать воздействие допустимыми пределами! Иначе можно что-нибудь угробить!
И учитываем периодичность измерения/воздействия.
UPD: кстати, насчет «периодичности» и временнЫх режимов.
Если вы реализуете свой алгоритм с помощью операционной системы реального времени, то там разумное учесть следующее:

• чтение текущего состояния (измерение ошибки) и воздействие должны быть вынесены в отдельный поток с максимально высоким приоритетом, т. к. весьма критична периодичность чтения/воздействия. Причем, эти потоки должны быть синхронны, но сдвинуты по фазе (другими словами, эти потоки должны вызываться с одинаковой периодичностью, но в разные моменты времени).
• расчет воздействия должен вестись в потоке с относительно низким приоритетом. Нет, ну он вообще-то может быть и весьма высоким, но однозначно ниже приоритета обработчиков прерываний и функций, непосредственно с ними — обработчиками прерываниями — связанными.
• также разумно поток вычисления воздействия сделать «спящим», а будить его должен поток измерения ошибки (после ее вычисления, конечно).
• возможна ситуация, что время воздействия пришло, а воздействие еще не рассчитано (т. к. разные приоритеты). Поэтому переменная с воздействием должна изменяться атомарно, да и считываться тоже: 1) меняться только в конце вычисления, 2) считываться только в одном месте потока воздействия. На худой конец повторится старое воздействие. Немного подпортит картинку, конечно, но потом, я думаю, система восстановится. Ну и нельзя забывать, что это в Си действия с float атомарные, на Ассемблере отнюдь! Похоже, что не обойтись без средств синхронизации/блокировки.

Я использую такой алгоритм:

Как видите – ничего революционного!
Прежде всего, все радости происходят в отдельной функции, которая вызывается периодически.
Первый вызов – инициализация из EEPROM или откуда-нибудь еще коэффициенты, обнуляем переменные для рекурсивных вызовов. Потом начинаем пошагово 1) измерять, 2) вычислять, 3) воздействовать, и так по кругу. Заодно производится привязка к реальному времени. Если текущее время меньше требуемого (функция TimeIsLower), то действие не производится.
В комментариях поинтересовались — зачем такие сложности с машиной состояний? С недетерминированным алгоритмом? Отвечаю: благодаря такому подходу я реализую простенький «параллелизм». Т. е. в промежутке между этапами вычислений я делаю какие-то другие действия (в моем случае общение по UART, которое может быть весьма напряженным — когда я использую сий девайс как логгер событий).
Вроде бы все… Что забыл, что перепутал – пишите. Как всегда, приветствуются комментарии о ляпах и ошибках!

P. S.Хочу поучаствовать в конкурсе, поэтому добавляю:

Видео:Теория автоматического управления. Лекция 16. Настройка ПИД-регулятораСкачать

Получить дискретную передаточную функцию и разностное уравнение пид регулятора

4.1. Цифровые регуляторы.

Как известно, наиболее важным функциональным узлом систем автоматического управления являются регуляторы, которые реализуются в микропроцессорной САУ программным путем и являются (из-за наличия в системе квантования по времени и уровню) цифровыми регуляторами.
Ограничиваясь рассмотрением линейных регуляторов, приведем классификацию цифровых регуляторов из [5].
Как видно из рис. 4.1, регуляторы разделяют на две группы: параметрически оптимизируемые и структурно оптимизируемые.
К параметрически оптимизируемым регуляторам относятся классические виды регуляторов типа П-регулятор, ПИ-регулятор, ПИД-регулятор и их модификации. К структурно оптимизируемым — компенсационные регуляторы и регуляторы состояния.
Компенсационные регуляторы проектируются с таким расчетом, чтобы снизить влияние некоторых параметров объекта на качество управления. При этом различают следующие модификации регуляторов этого типа:
— компенсатор — ликвидирует воздействие объекта в особых точках передаточной функции (нули и полюса);
— апериодический регулятор — обеспечивает окончание переходного процесса при ступенчатом возмущении за заданное время;
— регулятор-предиктор — регулятор с предсказанием реакции; модель объекта включается в обратную связь регулятора;
— регулятор с минимальной дисперсией — применяется в стохастических системах; минимизирует дисперсию значений регулируемой переменной.
Рассмотренные выше регуляторы называют регуляторами «входа-выхода», так как они контролируют входную и выходную величины и вырабатывают управляющее воздействие согласно определенному закону управления.
В отличие от этих регуляторов, регуляторы состояния контролируют характеристики вектора состояния объекта управления, описанного уравнениями в пространстве состояний. При наличии полной информации о векторе состояния применяется модальный регулятор в совокупности с модальным анализатором на входе и модальным синтезатором на выходе для синтеза реального вектора управления. Если некоторые переменные состояния невозможно измерить, используются регуляторы с наблюдате-

лями, восстанавливающими переменные состояния объекта.
В данном пособии мы ограничимся рассмотрением реализации в микропроцессорных системах некоторых регуляторов типа «вход-выход».

4.2. Алгоритмы цифровых регуляторов.

Наиболее распространенным регулятором, применяемым в системах управления динамическими объектами, является ПИД-регулятор и его модификации.
Аналоговый ПИД-регулятор имеет передаточную функцию вида , (4-1)

где К П — коэффициент передачи пропорциональной части регулятора, Т И — постоянная времени интегрирования, Т Д — постоянная времени дифференцирования.

Этой передаточной функции соответствует дифференциальное уравнение , (4-2)

где — выходная величина регулятора (управление), а — сигнал рассогласования.
При квантовании с малой длительностью такта Т это уравнение можно преобразовать в разностное с помощью дискретизации, заключающейся в замене производной разностью первого порядка, а интеграла — соответствующей интерполяционной формулой (по методу прямоугольников, трапеций, Симпсона и т.д.).
При использовании метода прямоугольников получаем . (4-3,а)

При использовании метода трапеций имеем . (4-3,б)

Для программной реализации в микропроцессорной системе более пригодны рекуррентные алгоритмы, в которых текущее значение управляющей переменной вычисляется через предыдущее значение и поправочный член , (4-4)

где, исходя из уравнений (4-3) для метода прямоугольников имеем , (4-5,a)

а, для метода трапеций (4-5,б)

Используя поправочный член , получаем рекуррентные выражения, описывающие динамику дискретного закона управления . (4-6)

Этому разностному уравнению соответствует дискретная передаточная функция регулятора , (4-7)

которая может быть получена из передаточной функции непрерывного регулятора (4-1) приближенным представлением оператора через оператор . В простейшем случае при использовании метода трапеций имеем . (4-8)

Согласно [5], существуют различные модификации дискретных ПИД-регуляторов.

Так, например, возможно повышение порядка регулятора за счет фильтрации сигнала рассогласования перед его дифференцированием. Этому закону управления в аналоговом регуляторе соответствует передаточная функция Рис. 4.2. Структура одноконтурной системы управления c дискретным регулятором. Произведя замену на , получим дискретную передаточную функцию регулятора более высокого порядка , (4-9) которой соответствует рекуррентное соотношение
, (4-10) где

B общем виде алгоритм работы регулятора описывается рекуррентным соотношением вида
, (4-10) что соответствует передаточной функции вида . (4-11) Обычно в регуляторах принимают ,а ; кроме того, исходя из требований нулевой статической ошибки, должно выполнятся условие .
Другой вид модификации регулятора заключается в раздельной обработке сигнала рассогласования и сигнала обратной связи , как показано на рис. 4.2. Это дает возможность избежать резких изменений управляющей переменной при резких изменениях сигнала задания .
В общем случае, вводя дополнительные параметры , получают обобщенный алгоритм цифрового регулятора в виде следующего рекуррентного выражения (4-12) Исходный алгоритм (4-10) получается при подстановке в (4-12) Таким образом, алгоритмы цифровых регуляторов могут быть построены на основании рекуррентных соотношений вида (4-10) или (4-12).
Рассмотрим реализацию ПИД-регулятора на базе микропроцессорной системы с использованием аппаратного таймера и системы прерываний. Схема алгоритма и временная диаграмма его работы показаны на рис. 4.3 и 4.4. Главная программа MAIN устанавливает начальное значение переменных, производит инициализацию всех устройств, разрешает прерывания и вызывает фоновую программу. По сигналу таймера формируется запрос на прерывание фоновой программы ЗПР 0 . В подпрограмме обслуживания этого прерывания INTER 0 обеспечивается вывод управляющего воздействия на ЦАП, либо передача его на программно-аппаратный драйвер исполнительного устройства, либо передача его на другой регулятор в случае многоконтурной (каскадной) САУ, а также запуск АЦП для измерения сигнала обратной связи y[n]. Сигнал готовности АЦП вызывает запрос на следующее прерывание ЗПР 1 и процессор переходит к подпрограмме обслуживания INTER 1 , где выполняется реализация алгоритма управления по рекуррентному соотношению ПИД-регулятора.
Как видно из временной диаграммы на рис. 4.4, время квантования Т задается таймером, вычисления по алгоритму регулятора начинаются по запросу ЗПР 1 и продолжаются в течение времени t РЕГ , а фоновая программа занимает оставшееся время и, кроме того, работает во время преобразования данных в АЦП. Требования к скорости вычислений, определяемой быстродействием процессора и сложностью алгоритма вытекают из необходимости соблюдения неравенства t РЕГ
Как видно из формул (4-10), (4-12), цифровой регулятор представляет собой рекурсивный фильтр. Сложный фильтр (регулятор) может быть эквивалентирован последовательным или параллельным соединением более простых фильтров. Реализацию таких систем программным путем иногда называют последовательным или параллельным программированием [1].
Если регулятор содержит интегральную составляющую, удобно представить его дискретную передаточную функцию в виде двух слагае — Рис. 4.3 Схема алгоритма цифрового ПИД-регулятора.

мых — интегратора и рекурсивного фильтра. Основными модулями алгоритма являются блок программной реализации интегратора И с ограничением и блок рекурсивного фильтра РКФ.
Как показано в [6], регулятор описывается дискретной передаточной функцией вида , (4-13,а) где К И =T/T И — коэффициент передачи интегратора, А i — коэффициенты РКФ, К — порядок РКФ.
Согласно ДПФ, представленной формулой (4-13,a), числовой код на выходе регулятора вычисляется как сумма N Р =N И +N Р.Ф. , где N И — код на выходе интегратора, определяемый по методу трапеций или

Рис. 4.4. Временная диаграмма выполнения алгоритма по схеме рис. 4.3.

прямоугольников, N Р.Ф . — код на выходе рекурсивного фильтра.
Для ограничения кода ошибки N е и кода на выходе интегратора N И и регулятора N Р используется макрокоманда LIM.
Алгоритм программной реализации работы цифрового регулятора с интегратором, построенным по методу правых прямоугольников, показан на рис. 4.5. Передаточная функция такого регулятора имеет вид . (4-13,б) Согласно формуле (4-13,б), код на выходе интегратора вычисляется, исходя из рекуррентного соотношения , (4-14) a, код на выходе рекурсивного фильтра представляет собой

В блоках 1 и 2 алгоритма, представленного на рис. 4.5, производится вычисление и ограничение сигнала рассогласования (ошибки) N е . В блоках 3 и 4 вычисляется интеграл от ошибки. Программе рекурсивного фильтра соответствуют блоки 5..11, а в блоках 12 и 13 вычисляется и ограничивается значение кода на выходе регулятора N Р .

4.3. Синтез цифровых регуляторов.

При достаточно малом периоде квантования Т (не превосходящем , где — наименьшая постоянная времени в системе) возможен синтез цифрового регулятора по непрерывному прототипу.

Рассмотрим для примера одноконтурную систему регулирования частоты вращения двигателя постоянного тока, структурная схема которой представлена на рис. 4.6,а. Она состоит из регулятора частоты вращения

Рис. 4.6. Одноконтурная система регулирования частоты вращения двигателя постоянного тока.

РЧВ, реализованного в микропроцессорной системе программно, вентильного силового преобразователя ВП и двигателя постоянного тока ДПТ, инерционность которого определяется двумя постоянными времени и , причем обычно Т М >>Т Я >Т ВП . Примем за аналоговый прототип РЧВ ПИД-регулятор с передаточной функцией, определяемой выражением (4-1) и приведем ее к следующему виду . (4-16) Выберем параметры регулятора так, чтобы скомпенсировать большие постоянные времени объекта управления и , т.е. примем . (4-17) Тогда структурная схема системы примет вид, показанный на рисунке 4.6,б. В этом случае передаточная функция замкнутой системы примет вид , (4-18) Где T’=T И /К, где К=К ВП К ДВ К ТГ К ОС .

Характеристический полином передаточной функции (4-18) обычно представляется в виде Т 1 2 р 2+2 x Т 1 р+1, где x — коэффициент колебательности, оптимальное значение которого для таких систем (т.е. около 0.707).
С учетом этого соотношения получим T’ И = 2T ВП , Откуда Т И = 2Т ВП К , (4-19) а передаточная функция замкнутой системы при таком выборе параметров регулятора будет иметь вид . (4-20) Таким образом, на основании уравнений (4-17) и (4-20) можно определить оптимальные параметры регулятора , а затем, выбрав период квантования , вычислить по формуле (4-5) коэффициенты передаточной функции цифрового ПИД-регулятора и осуществить конкретную настройку алгоритма его работы по рекуррентному соотношению (4-6). В реальных системах постоянная времени вентильного преобразователя составляет единицы мс, поэтому период квантования в таких системах должен быть, как правило, не более 1 мс, что предъявляет высокие требования к быстродействию аппаратуры и временной экономичности алгоритмов и программ вычислений.
Указанное ограничение особенно актуально для сложных многоконтурных систем управления, в которых существует несколько регуляторов, реализуемых в микропроцессорной системе программным путем последовательно.
В качестве иллюстрации вышеописанных особенностей рассмотрим цифровую трехконтурную следящую систему подчиненного управления, содержащую три каскадно включенных регулятора: регулятор положения, регулятор частоты вращения и регулятор тока. Структурная схема системы показана на рис. 4.7. Синтез регуляторов в такой системе производится, Рис. 4.7. Структурная схема следящей системы с каскадным включением регуляторов.

начиная с внутреннего токового контура, как наиболее быстродействующего; оптимальным для него является ПИ-регулятор, передаточная функция которого получается из (4-1) при Т Д =0. Порядок выбора оптимальных параметров и дискретизации тот же, как и при синтезе ПИД-регулятора. Наилучшим для данной системы регулятором частоты вращения (РЧВ) является П-регулятор, имеющий передаточный коэффициент К , оптимальное значение которого выбирается так же, как при синтезе ПИ-регулятора. Синтезированная система для внешнего контура показана на рис. 4.8,а, где

Если пренебречь достаточно малой постоянной времени Т 0 , получим идеальный следящий привод с передаточной функцией замкнутой системы , (4-21) где К РП — коэффициент передачи П-регулятора положения.
Как видно из (4-21), инерционность привода, его запаздывание Т ПР , обратно пропорционально добротности К w =К о К РП. Для того, чтобы уменьшить запаздывание и ошибку слежения в установившемся режиме (при движении с постоянной скоростью), в регулятор вводят дополнительную Рис. 4.8. Структурная схема внешнего контура следящей системы (а) и реализация регулятора положения с коррекцией по скорости.

коррекцию по скорости, как показано на рис. 4.8,а пунктиром. В этом случае установившаяся ошибка слежения будет определяться как , (4-22) где К n — коэффициент коррекции по скорости , Dj з — приращение координаты (угла поворота) за время квантования Т.
Оптимальным является соотношение К n =1/К w , а обычно выбирают К n w .

На рис. 4.8,б показана структурная схема одной из возможных реализаций цифрового регулятора положения с инкрементным датчиком, осуществляющего коррекцию по скорости.

Задание и сигнал обратной связи здесь представляются в виде приращений угла Dj з и Dj за время квантования Т. Поэтому регулятор содержит интегральную составляющую и способен выполнять коррекцию по скорости. Реализуемый им закон управления можно представить в виде

или при дискретизации и вычислении интеграла по методу прямоугольников (4-23).

Алгоритм работы цифрового регулятора по этой формуле показан на рис. 4.9.

Алгоритм работы цифрового регулятора рис. 4.9.

При больших величинах периода квантования применяются апериодические компенсационные регуляторы, синтез которых проводится по структурной схеме дискретной САР, переход к которой осуществляется дискретизацией объекта управления (объект представляется дискретной передаточной функцией D ОБ (z) ). Дискретная передаточная функция объекта управления может быть представлена в виде , (4-24)

причем обычно n

Работа обычного апериодического компенсационного регулятора ограничивается тем условием, что при ступенчатом воздействии переходный процесс должен закончится за m тактов. Тогда передаточная функция регулятора будет иметь вид , (4-25) a коэффициенты передаточной функции выбираются так, чтобы ее нули компенсировали полюса передаточной функции объекта управления. Кроме того, следует учесть, что p 1 +p 2 +. +p n =1, (4-26,a) q 0 +q 1 +. +q m =1/K. (4-26,б) Учитывая поставленные условия, получим Q(z)=A(z), B(z)=P(z) , откуда с учетом (4-26) можно вычислить значения коэффициентов регулятора через коэффициенты объекта управления q 1 =a 1 q 0 p 1 =b 1 q 0 q 2 =a 2 q 0 p 2 =b 2 q 0 . (4-27) q m =a m q 0 p n =b n q 0 q 0 =1/(b 0 +b 1 +. +b n ), q 0 =1/ [K(a 1 +a 2 +. +a m )].

Приведем пример синтеза цифрового регулятора частоты вращения для системы, структурная схема которой изображена на рис. 4.6. При пренебрежении инерционностью вентильного преобразователя ( Т ВП =0), передаточная функция объекта управления в системе, приведенной к виду, показанному на рис. 4.10 (a), будет равна Рис. 4.10. Структурная схема дискретной САР (а) и временная диаграмма изменения управляющего воздействия при ступенчатом управлении (б). , (4-28) где К=К ВП К ДВ К СС К ТГ .

Применив метод прямоугольников для выполнения дискретного интегрирования, получим дискретную передаточную функцию объекта .

где с М =Т М /Т, с Я =Т Я /Т .

Приведем передаточную функцию к стандартному виду , (4-29) где b 0 =К/(c М c Я +c М +1) , a 1 =-(2c М c Я +c М )/(c М c Я +c М +1), a 2 =(c М c Я )/(c М c Я +c М +1).

Передаточная функция апериодического регулятора будет иметь вид D (z)=q 0 +q 1 z -1 +q 2 z -2 , (4-30) где могут быть вычислены по формулам (4-27).
С целью получения рекуррентной формулы для вычисления управляющего воздействия, умножим числитель и знаменатель выражения (4-30) на ( 1-z -1 ) и получим дискретную передаточную функцию . (4-31) Из формулы (4-31) получаем рекуррентное соотношение для вычисления управляющего воздействия По формуле (4-32) может быть построен алгоритм работы регулятора, аналогично алгоритму рекурсивного фильтра, показанному на рис. 4.5.
При выборе периода квантования в апериодическом регуляторе следует исходить из того, что, поскольку синтез ведется из условия конечного времени управления при ступенчатом возмущении за m тактов, то при уменьшении периода квантования Т будет увеличиваться начальное управляющее воздействие u(0)=q 0 .
Так, для рассматриваемого регулятора частоты вращения из формулы (4-27) имеем соотношение q 0 =1/ b 0 = (c М c Я +c М +1)/ К = (T М T Я /T 2 +T М /T+1)/ К.

Приняв К=1 и Т М =10Т Я , получим

при T М /T=10	q 0 =u(0)=21
при T М /T=5	q 0 =u(0)=8.5
при T М /T=3	q 0 =u(0)=5
при T М /T=2	q 0 =u(0)=3.4

Рассчитаем значение управляющей переменной u[n ] при ступенчатом управлении Y=1. u [0]=q 0 ; u[1]=q 0 +q 1 =q 0 (1+a 1 ); u[2]=q 0 +q 1 +q 2 =q 0 (1+a 1 +a 2 ). Рассчитаем a 1 и a 2 для Т M /Т=3, получим a 1 =-0.98; a 2 =0.184 u [0]=q 0 =5; u[1]=0,1; u[2]=1.0

Временная диаграмма работы регулятора при единичном ступенчатом управлении показана на рис. 4.10,б. Как видно из диаграммы, при Т=Т M/3 для того, чтобы переходный процесс закончился за три такта, в первый такт регулятор должен воздействовать на объект с интенсивностью, в пять раз большей, чем в установившемся режиме, т.е. u[0]=5u[2].
Поэтому не следует выбирать слишком малые периоды квантования. Примерная рекомендация T>T S /m, (4-33) где T S — суммарная постоянная времени, а m — порядок объекта управления.

4.4. Алгоритмы пультовых операций и общая организация программного обеспечения.

В микропроцессорных системах обычно присутствует пульт оператора, посредством которого можно задавать различные режимы работы системы, вводить исходные данные, выводить определенную информацию о состоянии объекта и т.д. Пультовые режимы МПС поддерживаются программным обеспечением, в качестве примера которого может быть приведена встроенная операционная система «Монитор»; ее основными составляющими являются программы опроса пультовой клавиатуры, программы индикации, диспетчер режимов и т.п.
Рассмотрим более подробную программно-аппаратную организацию основных пультовых операций.
Работа с клавиатурой пульта . Можно выделить две основные фор-мы организации опроса клавиатуры: сканирование и опрос по прерыванию. В первом случае при необходимости определить состояние клавиатуры, основная программа передает управление процедуре, которая последовательно или последовательно-параллельно (группами), опрашивает состояние контактов клавиатуры; при этом каждому контакту может соот — Рис. 4.11. Организация последовательно-параллельного последовательного сканирования клавиатуры с унитарным кодированием. ветствовать один или несколько бит, т.е. определенный двоичный код (в частности, код КОИ-7 или Н-код). Во втором случае опрос клавиатуры осуществляется программой обслуживания, вызываемой автоматически по запросам прерывания, поступающим в контроллер при нажатии клавиши на клавиатуре; при этом, так же как в первом случае, клавише может соответствовать одинарный или комбинированный двоичный код.
При последовательно-параллельном сканировании, как показано на рис. 4.11,а, опрос осуществляется последовательным перемещением «0» в младших разрядах порта С4-С7. При этом считываемый столбец (полубайт) принимается старшими разрядами порта С0-С3, причем нажатой клавише соответствует «0», а не нажатой — «1».
В маломощных портах однокристальной микроЭВМ, в которых предусмотрена возможность побитной настройки разрядов порта, можно организовать последовательное сканирование, как показано на рис. 4.11,б. В этой системе столбцы также выбираются бегущим нулем в старших разрядах порта Р1 (Р1 .4-1. 7), настроенных на вывод, а принимается информация в выбранном столбце последова- тельно в младшие разряды порта (Р1 . 0-Р1 . 3) настройкой одного разряда на ввод, а всех других — на вывод нулей. На рис. 4.11,в показана схема считывания клавиатуры по запросупрерывания с кодированием клавиш. При нажатии клавиши через логическую схему ЛС в порт В пишется соответствующий код и одновременно формируется запрос прерывания ЗПР, по которому инициируется программа обслуживания, считывающая с порта В соответствующий клавише код. Рис. 4.12.a. Схема подсоединения восьмиразрядного динамического индикатора к порту ввода-вывода

Работа с устройствами отображения информации . Для индикации на пультах микропроцессорных систем часто используется линейка семисегментных светодиодных индикаторов, работающих в динамическом режиме, т.е. с последовательным обслуживанием разрядов с высокой частотой (примерно равной 1 кГц).
На рис. 4.12,а показана схема подсоединения восьмиразрядного динамического индикатора к порту ввода-вывода, в котором порт С через транзисторы по очереди подключает к питанию аноды семисегментных индикаторов, выбирая соответствующий разряд, а порт А выдачей нулей подключает катоды, задавая выводимый символ. Рис. 4.12.б. Схема подпрограммы динамической индикации INDIK
Схема подпрограммы динамической индикации INDIK показана на рис. 4.12,б. Подпрограмма вызывается по приходу прерываний от таймера, выставляемых им с промежутком, равным 1 мс, и поочередно выводит информацию на каждый разряд индикатора, т.е. за один проход программы выводится информация на один разряд. Таким образом, для хранения всей подлежащей индицированию информации в памяти контроллера должен быть организован массив — «регистр индикации» из n ячеек — по количеству разрядов индикатора. Кроме того, должны быть организованы программный счетчик адресов разрядов регистра индикации с циклическим переносом и регистр сдвига номера разряда индикатора, содержащий байт с одной «1», находящейся на месте, соответствующем номеру индицируемого разряда. Программа INDIK должна выполнять следующую последовательность действий:
1 — гашение индикатора записью в порт С всех нулей;
2 — опрос очередной ячейки регистра индикации по счетчику адресов этого регистра и увеличение счетчика на единицу;
3 — преобразование считанного кода в код управления сегментами индикатора;
4 — вывод преобразованного кода в порт А;
5 — формирование унитарного номера разряда, выводимого на индикатор сдвигом кода в регистре номера разряда;
6 — вывод этого кода в порт С. При этом подключается к питанию анод очередного индикатора и происходит его свечение до следующего запуска программы INDIK, т.е. в течение примерно 1 мс.
Программное обеспечение микропроцессорных систем управления обычно выполняется по модульному принципу и может быть разделено на программы, работающие в реальном времени по прерываниям, и программы, работающие в фоновом режиме. Работа ПО в фоновом режиме обычно организуется диспетчером режимов (для определенности названного далее PULT).

Инициализация программы PULT может происходить при включении источника питания, при выполнении программного сброса МПС, осуществляемого нажатием кнопки RESET, или макрокомандой операционной системы «Монитор», если таковая существует в данном варианте МПС.

Диспетчер режимов должен осуществлять переключение на выполнение различных программ в зависимости от состояния тумблеров пульта управления (ПУ), так как система может работать в различных режимах: рабочем, тестовом, наладочным и т.д. Для того, чтобы диспетчер режимов мог модифицировать и программы, работающие по прерываниям, удобно иметь программный регистр состояния системы (PCC, SSR), в котором отображается состояние переключателей ПУ и к которому могут обра — щаться все программы.

Примерный алгоритм программы диспетчера режимов приведен на рис. 4.13. Первые два блока (1 и 2) программы PULT обеспечивают начальную установку параметров — NUST — и инициализацию внешних устройств — INIT. Возможны два входа в программу: PULT.0 — с начальной установкой стандартных параметров и PULT.1 — с работой по нестандартным параметрам, которые должны быть заданы заранее до запуска программы PULT.

В блоке 3 диспетчер опрашивает переключатели ПУ, задающие различные режимы и программы работы МПС и отображает их состояние в регистре статуса системы — SSR, а затем переходит к выполнению рабочих фоновых программ. Рабочие фоновые программы и программы, работающие по прерыванию, при необходимости могут опрашивать регистр SSR для определения состояния ПУ. Часто бывает удобно иметь двойной SSR, в котором хранится и предыдущее состояние системы, так как иногда ход выполнения управляющей программы зависит от предыдущего состояния переключателей ПУ.

Для организации диалогового взаимодействия с микропроцессорной системой с помощью пульта оператора универсальные микроконтроллеры, такие, как, например, КПУ «Электроника МС 2702», имеют встроенную операционную систему — «Монитор».
Диалог “КПУ — пользователь” производится с пульта оператора. При задании на пульте очередной команды Монитора происходит прерывание рабочей программы и переход на обработку соответствующей команды.
Пользователь обращается к Монитору с помощью специальных команд. По окончании выполнения команды Монитора происходит передача управления на выполнение прерванной программы. Процесс ввода команды, а также результат ее выполнения отображаются обычно на дисплее пульта.

Команды Монитора (например, КПУ «Электроника МС 2702») по типу выполняемой ими функции можно разделить на три группы:
— команда управления выполнением программы — G;
— команды поддержки процесса отладки — E, S , J, A;
— сервисные команды — F, C, D, I, O, P, B.

Команда G (мнемоника “GO” — запустить) является командой запуска программы с определенного адреса или с адреса счетчика команд с возможными точками останова.
С помощью команды Е (“EMBARG” — загрузить) производится просмотр и модификация содержимого регистров микропроцессора.
По команде S (“SUBSTITUTE” — заменить) производится индикация и модификация содержимого памяти.
Команды J и A служат для установки и отмены режима трассировки при отладке программ.
Команды I и О служат для обращения к внешним устройствам (портам). Команда I (“INPUT” — ввод) производит индикацию содержимого регистра внешнего устройства по адресу, вводимому с пульта, а команда О (“OUTPUT” — вывод) производит вывод данных на регистр внешнего устройства.
Таким образом, Монитор представляет собой программный модуль диалогового взаимодействия пользователя с микропроцессорной системой.
Входными данными для Монитора являются его команды, а выходные данные представляют собой результаты выполнения команд, записываемые в ОЗУ или выдаваемые в виде сообщений на дисплее пульта или на внешних устройствах.
Так как реакция Монитора зависит от последовательности команд, задаваемой с пульта оператора, то он обычно строится как программный конечный автомат с памятью, имеющий определенное количество состояний, и выдающий выходные воздействия в зависимости от входных воздействий и своего внутреннего состояния, а также переходящий в новые состояния в зависимости от входных воздействий. Поэтому в Мониторе обычно реализуют программным путем автомат Мили или Мура, имеющий регистр состояния и определенные функции (матрицы) переходов и выходов. Программное обеспечение (ПО) микропроцессорной системы управления в соответствии с выполняемыми функциями можно разделить на три части:
— прикладное ПО — совокупность программ, разрабатываемых целевым образом для решения тех прикладных задач, для которых проектируется система — задач управления;
— ПО разработки программ — совокупность программ, используемых в качестве средств САПР прикладного ПО на всех этапах разработки программ для МПС с помощью отладочной системы;
— ПО вычислительного процесса — совокупность программ, предназначенных для организации вычислительного процесса в МПС и для контроля ее функционирования как при реализации прикладных задач,
и при ис пользовании микропроцессорной системы для разработки математического обеспечения. Рис. 4.14 Структура ПО МПС.

Подмножество программ, предназначенных для выполнения на данной микропроцессорной системе, называют ее резидентным программным обеспечением. Прикладное ПО и ПО вычислительного процесса являются резидентным программным обеспечением и располагаются в постоянной памяти программ микроконтроллера.

ПО, предназначенное для работы с микропроцессорной системой и ее программами, но реализованное на других, программно не совместимых с ней вычислительных средствах, называют кроссовым ПО данной микропроцессорной системы. К кроссовому ПО относят всевозможные программные отладчики, эмуляторы и симуляторы.

САПР-ПО может быть резидентным, кроссовым или смешанным.

Структура программного обеспечения микропроцессорных систем управления представлена на рис. 4.14.

🔍 Видео

Уроки Ардуино. ПИД регуляторСкачать

c12 4, Дискретные системы: Z преобразованиеСкачать

proТАУ: 1. Передаточная функцияСкачать

PID-регулятор. Коэффициенты и их настройка на простейшем примере.Скачать

Разностное функциональное уравнение решено двумя способами.Скачать

О PID регуляторе простым языком (что такое ПИДы)Скачать

7) ТАУ для чайников.Части 3.4 и 3.5 : Передаточная функция. Преобразование Лапласа...Скачать

Непрерывные законы регулированияСкачать

Как влияют параметры ПИД-регулятора на процесс? Ответ на вопрос 4Скачать

1) ТАУ (Теория автоматического управления) для чайников. Часть 1: основные понятия...Скачать

[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]Скачать

c12 1, Дискретные системы: определениеСкачать

Видеометодичка. Практикум по нахождению передаточных функций по дифференциальным уравнениямСкачать

Теория автоматического управления. Лекция 3. Дискретные САУ. ДПЛ и Z-преобразованиеСкачать

В.А. Александров «Синтез ПИД-регуляторов методом размещения полюсов»Скачать

ПИД регулятор теорияСкачать

Передаточные функцииСкачать

Основы теории автоматического управления. ПИД-регуляторСкачать