Кинематика материальной точки
1. Вектора. Запись векторов в декартовой системе координат. Модуль вектора.
2. Радиус-вектор. Запись радиус-вектора в Декартовых координатах.
3. Вектор скорости. Движение по инерции.
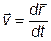
Пример:
Материальная точка, двигаясь равномерно и прямолинейно со скоростью V=5ex+2ey+7ez (м/с), На каком расстоянии от начала координат на расстоянии (в м) находится точка через 10с.
Скорость материальной точки задана уравнением v = 2ex +1ey+6 ez (м/c). Движение точки является равномерным, равноускоренным, равнозамедленным, с возрастающим ускорением или с убывающим ускорением?
Положение материальной точки задано уравнением r = 5t ex+ 1t 2 ey+ 0.5t 3 ez (м). Найти мгновенную скорость точки (в м/с) через 5с после начала движения.
4. Перемещение
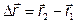
Пример:
Положение материальной точки задано уравнением r= 1tex+ 3t 2 ey+ 0.5t 3 ez (м). Найти перемещение (в м) за пятую секунду и модуль этого перемещения.
5. Траектория движения тела
Положение материальной точки задано уравнением r = 10t 2 ex+ 7ey+ 6t ez (м). Записать уравнение траектории движения тела.
6. Вектор ускорения.
Положение материальной точки задано уравнениемr =3t 2 ex+ 2t 2 ey+ t 2 ez (м). Найти вектор ускорения тела (в м/с 2 ) .
7. Типы движения. Равномерное, равноускоренное, равнозамедленное.
8. Нормальное и тангенциальное ускорения.
an=v 2 /R;
Материальная точка движется по окружности радиуса R= 20 см со скоростью V= 6t (м/с). Найти тангенциальное ускорение точки (в м/с 2 ) через 2 с от начала движения.
Материальная точка движется по окружности радиуса R=2 см со скоростью V=5м/с. Найти нормальное ускорение точки (в м/с 2 ).
9. Угловая скорость, Угловое ускорение.
Пример
Тело равномерно вращается по окружности радиуса 10 см с угловой скоростью ω=10 рад/с. Найти угловое ускорение (в рад/с 2 ):
10. Частота вращения, Число оборотов
Тело, равномерно вращается с угловой скоростью ω = 9.42 рад/с. Какова частота вращения (в об/с).
11. Уравнение кинематики равнопеременного вращательного движения
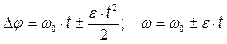
Пример 1:
Тело, вращаясь равнозамедленно, за 10 секунды изменило угловую скорость от ω1= 6 рад/с до ω2 = 1 рад/с. Найти угловое ускорение тела (в рад/с 2 ) .
Тело, вращаясь равноускоренно, за 10с от начала движения совершило 30 оборотов. Найти угловое ускорение тела (в рад/с 2 ).
Колесо радиусом 1м вращается согласно уравнению φ = 2-4t+0,1t 2 . Чему равна частота вращения колеса через t = 2с от начала отсчета времени.
Динамика материальной точки
- Сила. Нормальная и тангенциальная составляющие силы при криволинейном движении.
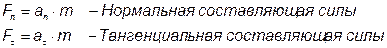
Пример:
Материальная точка массой 1 кг движется по окружности радиуса 1 м с возрастающей скоростью V= 3t (м/с). Найти нормальную составляющую силы, действующей на тело через 2 с от начала движения (в Н).

Найти координаты центра масс системы частиц с массами m1 = 15 кг и m2 = 20 кг, изображенной на рисунке.
Импульс материальной точки
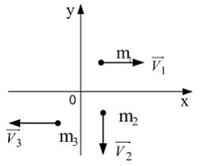
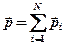
Пример:
Система состоит из трех шаров с массами 
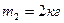
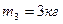
Cкорости шаров равны : 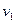

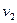
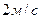
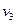
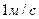
Второй закон Ньютона.
Материальная точка (тело массой 4 кг ) движется по окружности радиуса R= 2 см с возрастающей скоростью V= 2t (м/с). Найти тангенциальную составляющая силы, действующей на тело через 3 с от начала движения.
Тело массой 1 кг движется с ускорением 3 м/с 2 . Найти силу, действующую на тело.
Под действием результирующей силы 10Н у тела изменился импульс на 0.2 кг м/с. Найти время действия силы.
Скорость тела массой m = 1 кг изменяется по закону V = 1t ex+3t 2 ey+0.3t 3 ez (м/с). Найти модуль действующей силы через 1с от начала движения (в Н).
При взлете самолета пилот испытывает 2-кратные перегрузки. Найти ускорение самолета (в м/с 2 ).
Сила трения скольжения
Если коэффициент трения μ= 0,01 , то на тело массой m = 10 кг, движущееся по наклонной плоскости под углом 20 о к горизонту, действует сила трения
Сила Гравитации(Всемирного тяготения). Ускорение свободного падения(связь с законом всемирного тяготения)
Ускорение свободного падения на поверхности планеты:
Найти ускорение свободного падения на планете, масса которой в 3 раза меньше , чем у Земли, а радиус в 2 раза больше.
Сила натяжения подвеса. Вес тела.
Пример:
К нити подвешен груз массой 10 кг. Нить с грузом опускается с ускорением 5м/с 2 . Найти силу натяжения нити (в Н).
Силы вязкого трения.
Закон сохранения импульса
При выстреле из ружья массой 5 кг пуля массой 10 г летит со скоростью 600 м/с. Найти скорость отдачи ружья.
Катер, двигаясь со скоростью меньше критической, стал двигаться быстрее в 2 раза. Во сколько раз возросла сила сопротивления?
Пример:
Автомобиль массой 2т едет со скоростью 60 км/час по горизонтальной дороге. Коэффициент трения колес о дорогу μ = 0,5. Найти мощность двигателя (в кВт).
Инерциальная система отсчета.
Положения трёх тел относительно звезд изменяются по законам: 1) r1=3t ex+4t ey+1t ez(м), 2) r2=2t 2 ex +2t ey +5t 3 ez(м), 3) r3 = 6 ex + 5 ey + 1 ez (м). Системы отсчета, связанные с какими телами, являются инерциальными?
Видео:Определение кратчайшей расстоянии от точки до плоскостиСкачать

Физика-задачисеместр[1] (1). Физика, часть Кинематика и динамика материальной точки
| Название | Физика, часть Кинематика и динамика материальной точки |
| Анкор | Физика-задачисеместр[1] (1).doc |
| Дата | 06.03.2018 |
| Размер | 0.54 Mb. |
| Формат файла |  |
| Имя файла | Физика-задачисеместр[1] (1).doc |
| Тип | Документы #16294 |
| Подборка по базе: Экологические основы природопользования (ДО, СпДО, ПНК, КП, ПДО,, Теоретические основы начального курса математики с методикой пре, Брятова Л.И. Методические указания к выполнению лабораторных раб, Вторая часть Витязева.docx, 2 часть с отв.docx, Фильтрация нефти в пористой среде при наличии наночастиц графена, Английский Часть 1. письменная работа.pdf, введение, общая часть, специальная часть, заключение.docx, Экономическая часть.docx, СРС 2 часть матанализ.docx 1. Кинематика и динамика материальной точки. 1. Тело, вращаясь равноускоренно, за 6с от начала движения совершило 100 оборотов. Угловое ускорение тела равно (в рад/с 2 ) 2. Положение материальной точки задано уравнением r = 3t ex+2t 2 ey+1t 3 ez (м). Через 4с расстояние точки (в м) от начала координат равно 3. Колесо радиусом 30 см вращается согласно уравнению φ = 5-2t+0,2t 2 . В момент времени t = 4с от начала отсчета времени полное ускорение точек на ободе колеса равно (в м/с 2 ): 4. Графику зависимости скорости -: -: 5. Диск вращается вокруг своей оси, изменяя проекцию своей угловой скорости -: от 6. Тело брошено с поверхности Земли со скоростью 30 м/с под углом 60° к горизонту. Определите радиус кривизны его траектории в верхней точке. Сопротивлением воздуха пренебречь, g = 10 м/с 2 . 7. Под действием результирующей силы 10Н у тела изменился импульс на 5 кг м/с. Время действия силы равно (в с): 8.Материальная точка (m=2 кг) движется по окружности радиуса R= 2см с возрастающей скоростью V= 2t (м/с). Нормальная составляющая силы, действующей на тело через 2 с от начала движения, равна (в Н): 9. Брусок массой 0,1 кг покоится на наклонной плоскости.
10. Шарик массой -: 2. Механическая работа и энергия. 1. Потенциальная энергия тела на высоте 5 м от земли равна 80 Дж. Величина силы тяжести, действующей на тело, равна (в Н): 2. Чтобы сжатую на Х1= 3 см пружину с коэффициентом жесткости k=200 H/м сжать до Х2= 4 см, необходимо совершить работу (в мДж): 3. Потенциальная энергия гравитационного взаимодействия двух одинаковых материальных точек, находящихся на расстоянии 20 м друг от друга, равна 6,67 мкДж. Масса каждой из них равна (в т): 4. Зависимости потенциальной энергии тел №1 и №2 от высоты над поверхностью земли и их полная механическая энергия (Еполн ) представлены на рисунке. Кинетическая энергия тела №2 на высоте h=4 м равна (в Дж) : 5. Потенциальная энергия тела, вынужденного двигаться вдоль оси Х, имеет вид Епот.= кХ 4 , где к=10 6 Дж/м 4 . Сила, действующая на тело в точке с координатой 2см, равна (в Н): 6 -: в 3 раза больше, чем в точке В -: в 2 раза больше, чем в точке В -: в 2 раза меньше, чем в точке В -: в 3 раза меньше, чем в точке В 7 8. Тело массой 2 кг поднято над Землей. Его потенциальная энергия 900Дж. Если на поверхности Земли потенциальная энергия тела равна нулю и силами сопротивления воздуха можно пренебречь, то скорость, с которой оно упадет на Землю, составит… 9. Два тела двигались к стенке с одинаковыми скоростями и при ударе остановились. Первое тело катилось, второе скользило. Если при ударе выделилось одинаковое количества тепла, то больше масса тела . -: первого -: одинаковы -: второго 1. Два маленьких шара массами m1=50г и m2=10г закреплены на тонком невесомом стержне длиной 40 см (см. рис.). Момент инерции системы относительно оси ОО’ равен (в кг м 2 ): 2. Тонкий стержень длиной 5см, массой 120г вращается вокруг оси, проходящей через центр масс и перпендикулярной стержню. Суммарный момент внешних сил равен численно 0,001Нм. Угловое ускорение стержня равно (рад/с 2 ): 3. Вал радиусом 8 см и массой 40кг относительно оси АА’ имеет момент инерции (в кг . м 2 ): 4. Сплошной цилиндр массой 5 кг и радиусом 6 см катится без проскальзывания по горизонтальной поверхности со скоростью V = 4 м/с. Отношение его полной кинетической энергии к кинетической энергии вращения равно: 5. Вал радиусом 5см и массой 40кг вращается вокруг своей оси. Суммарный момент внешних сил равен 1Н•м . Угловое ускорение вала равно (в рад/с 2 ): 6. Момент импульса тела 7. Сплошной и полый цилиндры, имеющие одинаковые массы и радиусы, вкатываются без проскальзывания на горку. Если начальные скорости тел одинаковы, то… -: выше поднимется полый цилиндр -: оба тела поднимутся на одну и ту же высоту -: выше поднимется сплошной цилиндр 8. Если момент инерции тела увеличить в 2 раза, а скорость его вращения уменьшить в 2 раза, то момент импульса тела. -: уменьшится в 4 раза -: увеличится в 4 раза -: не изменится -: уменьшится в 2 раза 9. Диск и цилиндр имеют одинаковые массы и радиусы (рис.). Для их моментов инерции справедливо соотношение…
10. Потенциальная энергия тела на высоте 5м от земли равна 40Дж. Масса тела равна (в кг): 4. Релятивисткая механика. 1. Электрон движется со скоростью V =0,7c ( c- скорость света). Релятивистский импульс электрона ( me = 9,1х10 -31 кг) равен (в кг · м/с): 2. Если два фотона издалека летят навстречу друг другу, то они сближаются со скоростью (в м/с): — 3. На борту космического корабля нанесена эмблема в виде геометрической фигуры. Из-за релятивистского сокращения длины эта фигура изменяет свою форму. Если корабль движется в направлении, указанном на рисунке стрелкой, со скоростью, сравнимой со скоростью света, то в неподвижной системе отсчета эмблема примет форму, указанную на рисунке . -: 4. Физические явления в одинаковых условиях протекают одинаково во всех инерциальных системах отсчета – это принцип. -: независимости -: дополнительности -: относительности -: соответствия 5. Предмет движется со скоростью 0.8 с (с — скорость света в вакууме). Тогда его длина . -: увеличивается на 10% -: уменьшается на 10% -: увеличивается на 20% -: уменьшается на 40% 6. Скорость света в вакууме. -: зависит от длины волны -: зависит от скорости источника -: одинакова во всех инерциальных системах отсчета -: различна в разных системах отсчета 7.Относительно неподвижного наблюдателя тело движется со скоостью v. Зависимость массы этого тела от скорости при массе покоя m0 выражается соотношением. -: 8. Относительной величиной является. -: скорость света в вакууме -: барионный заряд -: длительность события -: электрический заряд 9. Скорость релятивистской частицы изменилась от V1=0,4с до V2=0,6с ( где с — скорость света).Её импульс увеличился в … раз. Ответ округлить до двух цифр после запятой. 10. Космический корабль с двумя космонавтами на борту, один из которых находится в носовой части ракеты, другой — в хвостовой, летит со скоростью -: меньше, чем -: больше, чем в 5. Молекулярно-кинетическая теория идеального газа. Основы термодинамики. 1. В сосуде под давлением 6х10 5 Па находится смесь кислорода, азота и аргона в одинаковых концентрациях. Парциальное давление аргона равно (в Па): 2. Если средняя квадратичная скорость молекул некоторого газа при температуре Т=300 К равна 1934 м/с, то название этого газа : 3. Плотность кислорода при температуре 320 К и давлении 1,92х10 5 Па равна (в кг/м 3 ): 4. На рисунке представлен график распределения Максвелла для водорода. Средняя арифметическая скорость молекул (в м/с) равна: 5. Средняя длина свободного пробега молекул азота при Р=1,05х10 5 Па и Т=300К равна (в м): 6. Если азот массой m = 28 г нагрели на 20 градусов, сообщив ему 415,5 Дж тепла, то молярная теплоемкость его равна 7. 7 молей газа расширяются изотермически от объема V1 = 2 л до объема V2 = 5,4 л. Прирост энтропии системы равен (в Дж/К) 8. Если у СО2 молярная теплоемкость при постоянном давлении равна 5хR/2 (где R – газовая постоянная), то число «замороженных» степеней свободы у него равно: 9. На (P, V)-диаграмме изображен циклический процесс.
-: повышается -: на CD-понижается, на DA- повышается -: понижается -: на CD- повышается, на DA- понижается -: 6. Механические колебания и волны. 1. Координата частицы массой 200г со временем изменяется по закону Х=5,4е –0,2 t cos(5t+π/6) (cм). Добротность системы равна 2. Приведенную длину физического маятника увеличили в 1,7 раза. Частота колебаний маятника изменилась: -: увеличилась в 1,7 раза -: увеличилась в 3,4 раза -: увеличилась в 1,5 раза -: уменьшилась в 1,3 раза -: уменьшилась в 3,4 раза 3. Частица массой 150г колеблется по закону Х= 3 cos (25t +π/6)(см). Коэффициент жесткости пружины равен (в Н/м): 4. Шарик, прикрепленный и насаженный на горизонтальную направляющую, совершает гармонические колебания. -: 5. Источник колебаний с периодом 0,004 с вызывает в воде звуковую волну с длиной волны 5,74 м. Скорость звука в воде равна (в м/с): 6. Если длина волны 7 м, а частота колебаний 220 Гц, то время прохождения волной расстояния 7,7км равно (в с): 7. Уравнение плоской волны в среде без затухания имеет вид: ξ(Х,t)=5cos(471t – 2х)(cм). Частота волны равна ( в Гц): 8. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ со скоростью 400 м/с, имеет вид -: 9. Если увеличить в 2 раза объемную плотность энергии и при этом уменьшить в 2 раза скорость распространения упругих волн, то плотность потока энергии… -: увеличится в 2 раза -: увеличится в 4 раза -: останется неизменной 10. Если ультразвуковой сигнал с частотой 60 кГц возвращается после отражения от морского дна с глубины 150 м через 0,2 с, то длина волны ультразвука в воде равна (в м) 7.Электростатическое поле в вакууме. 1 3. Если напряженность электрического поля равна Е= 6,8В/м, то сила, действующая на электрический заряд Q= 1,4Кл, равна (в Н) 4. В центре кольца радиусом R= 7см, равномерно заряженным с линейной плотностью заряда λ= 2,4нКл/м, потенциал электрического поля равен (в В): 5. Поток вектора напряженности однородного электрического поля напряженностью Е= 20 В/м через площадку радиуса r= 0,5м (см. рис.) при α= 60 о равен (в В·м):
7. Точечный заряд +q находится в центре сферической поверхности. Если добавить заряд +q внутрь сферы, то поток вектора напряженности электростатического поля -: уменьшится -: не изменится -: увеличится 8. В вершинах А и С квадрата ABCDнаходятся одноименные заряды q1= qи q2 =2 q . Если напряженность поля заряд q1в центре квадрата равна Е, то напряженность суммарного поля двух зарядов в этой точке будет равна. 9. Потенциал электрического поля изменяется по закону -: 1. На рисунке представлены кривые гистерезиса для двух сегнетоэлектриков. Максимальная поляризованность сегнетоэлектрика №2 (в условных единицах) равна: 2. Модуль вектора поляризации масла (ε=2,2) в электрическом поле напряженностью 23В/м равен (в 10 -10 Кл/м 2 ): 3. Если в плоском конденсаторе поверхностная плотность сторонних (свободных) зарядов равна 4нКл/м 2 , а поверхностная плотность связанных зарядов равна 2 нКл/м 2 , то модуль вектора электрического смещения равен (в нКл/м 2 ): 4. Заряд диполя Q=4,8 мкКл, плечо l=5 мм, то электрический дипольный момент его равен (в нКл·м): 5. Если напряженность электрического поля в парафине (ε=2) Е=3,6кВ/м , то электрическое смещение равно (в нКл/м 2 ): 6.Заряд Q = 3 нКл равномерно распределен внутри эбонитового шара радиусом R= 3 см. Дивергенция вектора электрического смещения в центре шара равна (в мкКл/м 3 ): 7. Явление гистерезиса, то есть запаздывания изменения вектора поляризации от изменения напряженности внешнего электрического поля, имеет место в . -: полярных диэлектриках -: неполярных диэлектриках -: сегнетоэлектриках -: любых диэлектриках 8. Если внести неполярный диэлектрик в электрическое поле, то … -: возникнет пьезоэлектрический эффект -: у молекул возникнут дипольные моменты, ориентированные в направлении, противоположном направлению линий напряженности внешнего электрического поля -: жесткие диполи молекул будут ориентироваться в среднем в направлении вдоль вектора напряженности электрического поля -: у молекул возникнут индуцированные дипольные моменты, ориентированные по направлению линий напряженности электрического поля -: электрическое поле внутри диэлектрика не изменится 9. Внутри стекла (ε=7) напряженность электрического поля равна 150 В/м. Плотность энергии электрического поля в нем равна (в мкДж/м 3 ) 10. Если значение вектора поляризации масла (ε=2,2) равно 4 нКл/м 2 , то диэлектрик находится в электрическом поле напряженностью (в В/м): 1. В конденсаторе емкостью С= 3,4 мкФ при разрядке через сопротивление R=4,3 МОм заряд уменьшится в 2,72 раза за время (в с) 2. Конденсатор с электроемкостью С= 3 пФ при разности потенциалов на обкладках конденсатора U= 220 В имеет заряд (в нКл) 3. Изолированный проводник, находящийся в вакууме, заряжен с поверхностной плотностью заряда σ= 6 нКл/м 2 . Снаружи возле его поверхности напряженность электрического поля равна (в В/м) 4. В проводнике, по которому течет ток плотностью j=3 х10 6 А/м 2 , напряженность электрического поля равна E=66 мВ/м. Удельное сопротивление проводника равно (в нОм·м) 5. Если напряженность электрического поля Е=100В/м, электрическое смещение D=2нКл/м 2 , то плотность энергии этого поля равна (в нДж/м 3 ): 6. Уединённый проводник с зарядом 0,7нКл имеет потенциал 5,5В. Его электроемкость равна (в нФ): 7. Электроемкость системы конденсаторов С1=12пФ, С2=24пФ, С3=24пФ, С4=8пФ равна (в пФ): 8. В электрическом поле плоского конденсатора перемещается заряд + q в направлении, указанном стрелкой.
-: равна нулю -: отрицательна -: положительна 9. На проводнике с электроемкостью С=45мкФ находится заряд Q=1мКл. Потенциал проводника равен (в кВ) 10. В плоском слюдяном (ε=7) конденсаторе, площадь каждой пластины которого равна 0,8 см 2 и расстояние между ними 0,4мм, электроемкость равна (в пФ): 11. Если (см. рис.) R1= 5 Ом, R2= 4 Ом, R3= 3 Ом, то сопротивление всей цепи равно (в Ом): 12. Если напряженность электрического поля Е= 125 В/м, электрическое смещение D=7 нКл/м 2 , то плотность энергии этого поля равна (в нДж/м 3 ) 13. Энергия взаимодействия зарядов q1= -6 мкКл и q2 = -3 мкКл (см рис.) равна (в Дж): 10. Электрический ток. 1. На рисунке дана зависимость силы тока от напряжения. 2. В электрической цепи с ЭДС=2,5В, внутренним сопротивлением 0,1Ом при силе тока I= 2,3А сопротивление нагрузки равно (в Ом): 3. Если уменьшить в два раза напряженность электрического поля в проводнике, то удельная тепловая мощность тока … -: увеличится в два раза; -: не изменится; -: уменьшится в 4 раза -: уменьшится в два раза; -: увеличится в 4 раза; 4. В медном проводе длиной L=1,5 м, сечением S=2 мм 2 при разности потенциалов на концах провода U=5 В протекает ток силой (в А): 5. Если утюг мощностью P=1,6кВт в течение t=20мин включен в цепь, то при стоимости 1,8 руб за кВт·час потратится энергии (в руб) 6. Удельная тепловая мощность в медном проводнике при плотности тока j= 40А/м 2 равна (в мкДж/(м 3 ·с)): 7. Вольтамперная характеристика активных элементов 1 и 2 цепи представлена на рисунке. 8. На рисунке дана вольтамперная характеристика для трех проводников №1,№2 ,№3. Электропроводимость проводника № 1 равна (в См): 9. Если увеличить в2 раза напряжение между концами проводника, а площадь его сечения уменьшить в 2 раза, то сила тока, протекающего через проводник. -: уменьшится в4 раза -: увеличится в 4 раза Видео:Задача 7. Найти расстояние от точки M0 до плоскости, проходящей через три точки M1, M2, M3.Скачать  Движение материальной точки задано уравнением r t i tj k 4 3 2 2 , м.
👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение. ➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб. ➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам. ⚡ Условие + 37% решения: Движение материальной точки задано уравнением r t i tj k 4 3 2 2 , м. Найдите, как изменяются с течением времени координаты точки и проекции ускорения на оси координат. Чему равняется ускорение в момент времени t 2 c . Решение Положение материальной точки в пространстве задается радиус-вектором r : r xi yj zk Где i , j , k – – единичные векторы направлений; x , y , z – координаты точки. Согласно условию задачи, движение материальной точки задано уравнением: r t i tj k 4 3 2 2 Из двух последних выражений можем записать: 2 x t 4t ; yt 3t ; zt 2 Найдем скорость х : t dt d t dt dx х 8 4 2 Найдем скорость y : 3 3 dt d t dt dy y Найдем скорость z : 0
Готовые задачи по физике которые сегодня купили: Образовательный сайт для студентов и школьников Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника. © Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института Видео:Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать  Уравнение движения материальной точкиДвижение материальной точки в пространстве – это изменение ее положения относительно других тел с течением времени. Имеет смысл говорить только о движении в некоторой системе отсчета. Видео:Составьте уравнение плоскости, проходящей через ось Оу и точку M (3;2;4).Скачать  Система отсчета. Системы координатТочки, располагаемые в пустом пространстве, не различаются. Поэтому о точке рассуждают при условии нахождения в ней материальной точки. Определить ее положение можно при помощи измерений в системе координат, где и проводится нахождение пространственных координат. Если рассматривать в виде примера поверхность Земли, то следует учитывать широту и долготу располагаемой точки. В теории используется декартова прямоугольная система координат, где определение точки возможно при наличии радиус-вектора r и трех проекций x , y , z – ее координат. Могут быть применены другие:
В теории зачастую не принимают во внимание реальную систему отсчета, а сохраняют только ту, которая представляет собой ее математическую модель, применяемую во время практических измерений. Видео:Уравнение плоскости через 3 точкиСкачать  Кинематическое уравнение движения материальной точкиЛюбая система отсчета или координат предполагает определение координат материальной точки в любой момент времени. При условии положения и определения материальной точки в данной системе отсчета считается, что ее движение задано или описано. Это возможно при использовании кинематического уравнения движения: Аналитически положение точки определяется совокупностью трех независимых между собой чисел. Иначе говоря, свободная точка имеет три степени свободы движения. Ее перемещение по уравнению ( 1 ) определено, если имеется указанное положение в любой момент времени t . Для этого следует задавать декартовы координаты точки в качестве однозначных и непрерывных функций времени: x ( t ) = x , y ( t ) = y , z ( t ) = z ( 2 ) . Прямоугольные декартовы координаты x , y , z — это проекции радиус-вектора r ¯ , проведенного из начала координат. Очевидно, что длину и направление r ¯ можно найти из соотношений, где a , β , γ являются образованными радиус-вектором углами с координатными осями. Равенства ( 2 ) считают кинематическими уравнениями движения материальной точки в декартовых координатах. Они могут быть записаны в другой системе координат, которая связана с декартовой взаимно однозначным преобразованием. Если движение точки происходит в плоскости О х у , тогда применимы полярные координаты r , φ , относящиеся к декартовым преобразованиям. Данный случай подразумевает использование уравнения движения точки следующего вида: r = r ( t ) , φ = φ ( t ) ( 3 ) . Кинематическое уравнение движения точки в криволинейных координатах q 1 , q 2 , q 3 , связанных с декартовыми преобразованиями вида x = x ( q 1 , q 2 , q 3 ) , y = y ( q 1 , q 2 , q 3 ) , z = z ( q 1 , q 2 , q 3 ) ( 4 ) , записывается как q 1 = q 1 ( t ) , q 2 = q 2 ( t ) , q 3 = q 3 ( t ) ( 5 ) . Кривая радиус-вектора, описываемая концом вектора r при движении точки, совпадает с ее траекторией. Параметрическое уравнение траектории с t представлено кинематическими уравнениями ( 2 ) , ( 5 ) . Чтобы получить координатное уравнение траектории следует исключить время из кинематических уравнений. Определение движения точки возможно с помощью задания траектории и мгновенного положения точки на ней. Ее положение на кривой определяется с помощью указания только одной величины: расстояния вдоль кривой от некоторой начальной точки с положительным направлением: Это и есть уравнение движения точки по траектории. Способ его задания относят к естественному или траекторному. Понятия координатного и естественного способа задания движения точки физически эквивалентны. С математической стороны это рассматривают как возможность применения разных методов, исходя из случая математической задачи. Задание такого закона возможно аналитическим, графическим путем или с использованием таблицы, последние два из которых зачастую рассматривают в виде графиков и расписаний движений поездов. Дано уравнение движения материальной точки x = 0 , 4 t 2 . Произвести запись формулы зависимости υ x ( t ) , построить график зависимости скорости от времени. На графике отметить площадь, численно равную пути, пройденному точкой за 4 секунды, произвести вычисление. Дано: x = 0 , 4 t 2 , t = 4 c Найти: υ x ( t ) , S — ? Решение При решении необходимо учитывать зависимость скорости от времени: υ x = υ 0 x + a x t . Зависимость координаты от времени и сравнение уравнения с заданным принимает вид: x = x 0 + υ 0 x t + a x t 2 2 , x = 0 , 4 t 2 . Очевидно, что x 0 = 0 , υ 0 x = 0 , a x = 0 , 8 м / с 2 . После подстановки данных в уравнение: Определим точки, изобразим график: υ x = 0 , t = 0 , υ x = 4 , t = 5 Путь, по которому двигалось тело, равняется площади фигуры, ограниченной графиком, и находится с помощью формулы: 🔥 ВидеоВекторный метод в стереометрии. Задача 14 профильный ЕГЭСкачать  Кинематика точки. Три способа задания движения. Скорость, ускорениеСкачать  Расстояние от точки до плоскости / Вывод формулыСкачать  Определение параметров движения по заданному радиус-вектору. Векторный способ задания движения.Скачать  1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать  Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать  №578. Найдите координаты центра и радиус сферы, заданной уравнением: а) х2+y2+z2 = 49; б) (x — 3)2Скачать  Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать  2 3 проекция точки на конусеСкачать  2.4. Радиус-вектор и вектор перемещенияСкачать  Построение параллельной плоскости на расстояние 40 мм. Плоскость задана со следами.Скачать  1 2 4 сопряжение окружностейСкачать  Радиус-векторыСкачать  Урок 3 Определение координаты движущегося телаСкачать  Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать  |
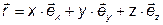
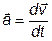
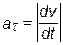
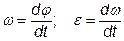
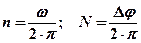
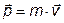
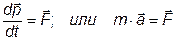
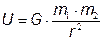

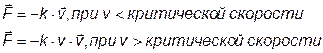
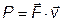
 от времени
от времени  соответствует уравнение.
соответствует уравнение. -:
-: 


 так, как показано на рисунке. Вектор угловой скорости
так, как показано на рисунке. Вектор угловой скорости  направлен по оси
направлен по оси  , а вектор углового ускорения
, а вектор углового ускорения  направлен против оси
направлен против оси 
 до
до  -: от 0 до
-: от 0 до  -: от
-: от до
до  Величина силы трения равна….
Величина силы трения равна…. упал с высоты
упал с высоты  на стальную плиту и упруго отскочил от неё вверх. Изменение импульса шарика в результате удара равно…
на стальную плиту и упруго отскочил от неё вверх. Изменение импульса шарика в результате удара равно… -:
-:  -:
-:  -:
-: 

 . Небольшая шайба начинает движение без начальной скорости по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты х изображена на графике U(x).Кинетическая энергия шайбы в точке С
. Небольшая шайба начинает движение без начальной скорости по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты х изображена на графике U(x).Кинетическая энергия шайбы в точке С . На рисунке показан вектор силы, действующей на частицу. Работа, совершенная этой силой при перемещении частицы из начала координат в точку с координатами (5; 0), равна .
. На рисунке показан вектор силы, действующей на частицу. Работа, совершенная этой силой при перемещении частицы из начала координат в точку с координатами (5; 0), равна .  -:
-:  -:
-:  -:
-: 


 изменяется со временем по закону
изменяется со временем по закону  .Момент действующих на тело сил станет равен нулю через…
.Момент действующих на тело сил станет равен нулю через… -:
-:  -:
-:  -:
-: 
 : 0,3х10 8 -: 2х10 8 -: 3х10 8 -: 6х10 8 -: 8х10 8
: 0,3х10 8 -: 2х10 8 -: 3х10 8 -: 6х10 8 -: 8х10 8 -:
-:  -:
-: 
 -:
-:  -:
-:  -:
-:  -:
-:
 . Космонавт, находящийся в хвостовой части ракеты, производит вспышку света и измеряет промежуток времени
. Космонавт, находящийся в хвостовой части ракеты, производит вспышку света и измеряет промежуток времени  , за который свет проходит расстояние до зеркало, укрепленного у него над головой, и обратно к излучателю. Этот промежуток времени с точки зрения другого космонавта.
, за который свет проходит расстояние до зеркало, укрепленного у него над головой, и обратно к излучателю. Этот промежуток времени с точки зрения другого космонавта. -: 752 -: 2825 -: 3050 -: 2500 -: 1,223х10 -20
-: 752 -: 2825 -: 3050 -: 2500 -: 1,223х10 -20 На участках CD и DA температура.
На участках CD и DA температура. -:
-:  -:
-:  -:
-: 
 На графике представлена зависимость проекции силы упругости пружины на положительное направление оси
На графике представлена зависимость проекции силы упругости пружины на положительное направление оси  от координаты шарика.
от координаты шарика. Работа силы упругости на участке
Работа силы упругости на участке  равна…
равна… -:
-:  -:
-:  -:
-: 
 Волновое число k равно.
Волновое число k равно. -:
-:  -:
-: 
 . Если в электрическом поле заряженной большой металлической плоскости расположены две одинаковые площадки 1 и 2, а угол α= 60 градусов, то отношение потоков ФЕ2 к ФЕ1 равно:
. Если в электрическом поле заряженной большой металлической плоскости расположены две одинаковые площадки 1 и 2, а угол α= 60 градусов, то отношение потоков ФЕ2 к ФЕ1 равно: -: 0,785 -: 36 -: 15,08 -: 15,70 -: 7,85
-: 0,785 -: 36 -: 15,08 -: 15,70 -: 7,85 через поверхность сферы…
через поверхность сферы… -:
-:  -:
-:  -:
-:  -:
-:
 , где
, где  — постоянный вектор,
— постоянный вектор,  радиус-вектор точки поля. Напряженность этого поля равна.
радиус-вектор точки поля. Напряженность этого поля равна. =
=  -:
-:  -: 4 -: 5 -: 8 -: 2 -: 3
-: 4 -: 5 -: 8 -: 2 -: 3
 Тогда работа сил поля на участке АВ…
Тогда работа сил поля на участке АВ…

 Мощность, выделяемая на сопротивлении, при U = 40В равна (в Вт):
Мощность, выделяемая на сопротивлении, при U = 40В равна (в Вт): При напряжении 40 В отношение мощностей
При напряжении 40 В отношение мощностей  равно
равно





