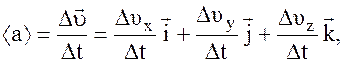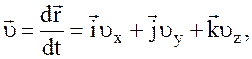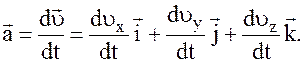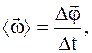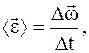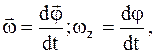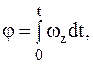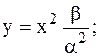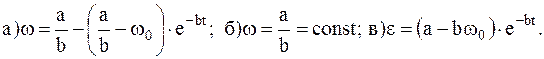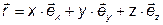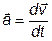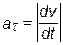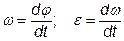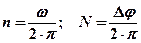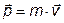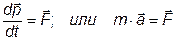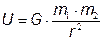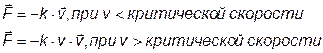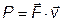Положение материальной точки задано уравнением

1. Положение материальной точки в пространстве задается радиус-вектором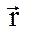

,

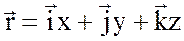
где 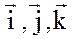– единичные векторы декартовой системы координат (орты); x, y, z – координаты точки.

Средние скорость и ускорение

Средний вектор скорости

где 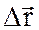– перемещение материальной точки за интервал времени Dt; – средние значения проекций скорости на координатные оси; Dx=x(t)–х₀; Dy=y(t)–y₀; Dz=z(t)–z₀ – проекции перемещения материальной точки за интервал времени Dt; x₀, y₀, z₀ – начальное положение точки в пространстве.

Среднее значение скорости:

,

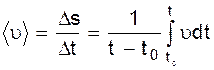
где Ds – пройденный путь за интервал времени Dt=t–t₀.

Средний вектор ускорения

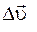
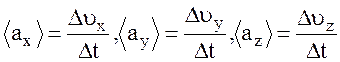
где – приращение вектора скорости материальной точки за интервал времени Dt.

– средние значения проекций ускорения на координатные оси.

Среднее ускорение ,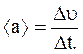

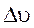
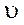
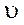
где = (t)- (t₀) .

Мгновенные скорость и ускорение

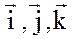
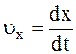
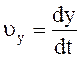
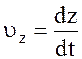
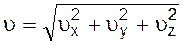
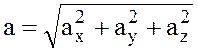
где – единичные векторы (орты осей декартовой системы координат); ; ; – проекции скорости на координатные оси.

.

.

Кинематические уравнения движения

Кинематическое уравнение движения материальной точки в векторной форме

,

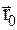
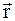
где – радиус-вектор материальной точки в начальный момент времени t₀; – радиус-вектор в произвольный момент времени t, закон изменения скорости точки со временем.

Векторное уравнение движения эквивалентно трем скалярным:

, ,

.

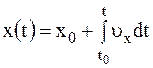
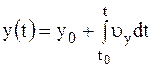
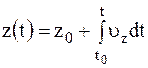
Кинематическое уравнение равномерного прямолинейного движения материальной точки вдоль оси x

Кинематическое уравнение равнопеременного прямолинейного движения (a=const) вдоль оси x

Скорость точки при равнопеременном движении вдоль оси x

Связь скорости и ускорения

Средние угловая скорость и ускорение

Средний вектор угловой скорости

где 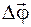– приращение угла поворота за интервал времени Dt .

Средний вектор углового ускорения

где 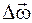– приращение угловой скорости за интервал времени Dt.

Средняя угловая скорость

, где = φ(t)- φ(t₀).

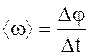
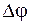
Среднее угловое ускорение

, где =ω(t)-ω(t₀).

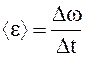
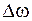
Мгновенные угловая скорость и ускорение

Мгновенная угловая скорость

где w_z – проекция угловой скорости на ось вращения.

Угловое ускорение ,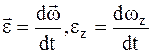

где e_z – проекция углового ускорения на ось вращения.

Угловая скорость и угловое ускорение являются аксиальными векторами, их направления совпадают с неподвижной в пространстве осью вращения.

Связь между линейными и угловыми величинами:

S=Rj; u=wR; a_t=e_zR; a_n= 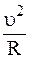=w 2 R,

где R – радиус окружности, по которой движется точка; S – длина дуги окружности; j – угол поворота, u – линейная скорость; e_z – проекция углового ускорения на ось вращения; w – угловая скорость; a_t – тангенциальное ускорение; a_n – нормальное ускорение.

При постоянной угловой скорости w=2p/T, w=2pn, где Т – период (время одного полного оборота); n – частота вращения (число оборотов, совершаемых движущейся точкой в единицу времени).

Кинематическое уравнение вращательного движения материальной точки относительно неподвижной оси

где j – угол поворота; w_z – проекция угловой скорости на ось вращения. Если w_z=const, то j=w_zt. Если угловое ускорение e=const, то 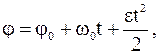где w₀ – начальная угловая скорость. Угловая скорость при таком вращении

Ускорение в плоском криволинейном движении

или
,

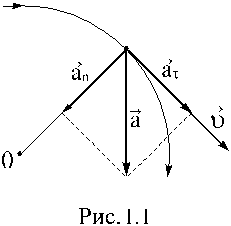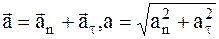
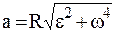
где характеризует быстроту изменения модуля скорости (см. рис. 1.1);

a_n = — характеризует быстроту изменения вектора скорости по направлению ( см. рис. 1.1).

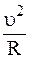
Соответствие линейных и угловых величин показано в табл.1.

Линейные величины	Угловые величины
S,х	φ
υ	ω
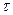а	e
an=	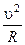an=ω 2 R
ux=u0x+axt	wz=w0z+ezt
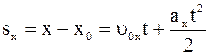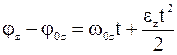2axsx=ux 2 –u0x 2	2ezjz=wz 2 –w0z 2

СПРАВОЧНЫЙ МАТЕРИАЛ

Заряд электрона e=1,6×10 -19 Кл.

Масса электрона m=9,1×10 -31 кг.

Ускорение свободного падения g=9,8 м/с 2 .

ВОПРОСЫ И УПРАЖНЕНИЯ

1. Что изучает механика как один из разделов физики?

2. Почему при изучении реальных физических явлений и объектов приходится использовать модельные представления и абстрагированные понятия? Дайте определение: а) материальной точке (частице); б) системе материальных точек; в) абсолютно твердому телу.

3. Каково содержание понятий пространства и времени в классической механике? Что означают понятия «однородность и изотропность пространства», «однородность времени»?

4. Какие существуют способы описания движения материальной точки? Что представляет собой система отсчета, система координат? Что называется радиусом-вектором ?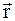

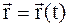
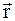
5. Покажите, что задание кинематического закона движения в координатной форме х=х (t), у=у (t), z=z (t) эквивалентно заданию его в векторной форме , где х, у, z – декартовы координаты положения материальной точки, – ее радиус-вектор. Каковы преимущества векторного описания движения?

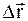
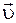
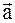
6. Дайте определение кинематических величин: а) перемещения ; б) скорости ; в) ускорения . В каких единицах измеряются эти величины? Как ориентированы векторы скорости и ускорения относительно траектории и друг друга?

7. Частица движется по закону где u₀ и g – известные постоянные; – орт координатной оси z. Найдите скорость частицы и ее ускорение , а также их проекции и как функции времени.

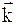
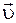
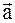
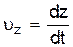
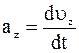
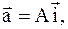
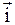
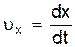
8. Ускорение движущейся частицы где A – известная постоянная; – орт координатной оси х. В момент времени t=0 х=x₀ и u_x=u₀, где х₀ и u₀ – известные постоянные (начальные условия). Найдите проекцию скорости и координату x как функции времени.

9. Какое движение абсолютно твердого тела называется: а) поступательным; б) вращательным? Приведите примеры таких движений.

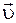
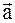
10. Что называется тангенциальным а_t и нормальным а_n ускорениями? Чему они равны? От чего зависит угол между векторами скорости и полного ускорения движущейся материальной точки?

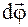
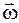
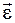
11. Какие векторы называют аксиальными? Дайте определение: а) угла поворота твердого тела; б) угловой скорости ; в) углового ускорения относительно неподвижной в пространстве оси вращения. В каких единицах измеряются эти величины?

12. Колесо вращается вокруг неподвижной оси, проходящей через его центр масс. Обладает ли любая точка на ободе тангенциальным и нормальным ускорениями, если вращение происходит: а) с постоянной угловой скоростью; б) с постоянным угловым ускорением? Изменяются ли при этом модули этих величин?

ЗАДАЧИ ГРУППЫ А

1.(1.25) Зависимость пройденного телом пути s от времени t дается уравнением s=A+Bt+Ct 2 +Dt 3 , где С=0,14 м/с 2 и D=0,01 м/с 3 . Через какое время t после начала движения тело будет иметь ускорение a=1 м/с 2 ? Найти среднее ускорение тела за этот промежуток времени.

Ответ: t=12 c, =0,64 м/с 2 .

2.(1.27) Камень, брошенный горизонтально, упал на землю через время t=0,5 с на расстоянии l=5 м по горизонтали от места бросания. С какой высоты h брошен камень? С какой скоростью u_x он брошен? С какой скоростью u он упадет на землю? Какой угол j составит вектор скорости камня с горизонтом в точке его падения на землю.

Ответ: h=1,22 м; u_x=10 м/с; u=11,1 м/с; j=26 0 12 ’ .

3.(1.30) Камень брошен горизонтально со скоростью u₀=15 м/с. Найти нормальное а_n и тангенциальное а_t ускорения камня через время t=1 с после начала движения.

Ответ: а_t=5,4 м/с 2 ; а_n=8,2 м/с 2 .

4.(1.31) Камень брошен горизонтально со скоростью u₀=10 м/с. Найти радиус кривизны R траектории камня через время t=3 с после начала движения.

Ответ: R=305 м.

5.(1.39) С башни высотой h₀=25 м брошен камень со скоростью u₀=15 м/с вверх под углом a=30 0 к горизонту. Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадет на землю? С какой скоростью u он упадет на землю? Какой угол j составит траектория движения камня с горизонтом в точке его падения на землю?

Ответ: t=3,16 c; l=41,1 м; u=26,7 м/с; j=61 0 .

6.(1.49) Вентилятор вращается с частотой n=900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N=75 об. Какое время t прошло с момента выключения вентилятора до полной его остановки?

Ответ: t=10 c.

7.(1.52) Точка движется по окружности радиусом R=20 см с постоянным тангенциальным ускорением а_t. Найти тангенциальное уско-рение а_t точки, если известно, что к концу пятого оборота после начала движения линейная скорость точки u=79,2 см/с.

Ответ: а_t=0,05 м/с 2 .

8.(1.55) Колесо радиусом R=10 см вращается с угловым ускорением e 3,14 рад/с 2 . Найти для точек на ободе колеса к концу первой секунды после начала движения: а) угловую скорость w; б) линейную скорость u; в) тангенциальное ускорение а_t; г) нормальное ускорение а_n; д) полное ускорение а; е) угол a, составляемый вектором полного ускорения с радиусом колеса.

Ответ: а) w=3,14 рад/с; б) u=0,314 м/c; в) a_t=0,314 м/c 2 ;

г) a_n=0,986 м/c 2 ; д) a=1,03 м/c 2 ; е) a=17 0 46 ’ .

9.(1.57) Точка движется по окружности так, что зависимость пути от времени дается уравнением s=A–Bt+Ct 2 , где В=2 м/c и С=1 м/c 2 . Найти линейную скорость u точки, ее тангенциальное а_t, нормальное а_n и полное а ускорения через время t=3 с после начала движения, если известно, что при t¢=2 с нормальное ускорение точки а¢_n=0,5 м/c 2 .

Ответ: u=4 м/c; a_t=2 м/c 2 ; a_n=2 м/c 2 ; a=2,83 м/c 2 .

10.(1.64) Во сколько раз нормальное ускорение а_n точки,лежащей на ободе вращающегося колеса, больше ее тангенциального ускорения а_t для того момента, когда вектор полного ускорения точки составляет угол a=30 0 с вектором ее линейной скорости?

ЗАДАЧИ ГРУППЫ Б

1.(1.4) По прямой линии движутся две материальные точки согласно уравнениям: x₁=А₁+В₁t+C₁t 2 и x₂=А₂+В₂t+С₂t 2 , где А₁=5 м, В₁=1 м/с, С₁=2 м/с 2 , А₂=–6 м, В₂=4 м/с, С₂=0,8 м/с 2 . В какой момент времени t скорости этих точек будут одинаковы? Найти скорости u₁, u₂ и ускорения a₁, a₂ этих точек в момент времени t₁=1c.

Ответ: t=1,25 c; u₁=5 м/с; u₂=5,6 м/с; а₁=4 м/с 2 ; а₂=1,6 м/с 2 .

2.(1.23) Кинематические уравнения движения двух материальных точек имеют вид x₁=A₁t+B₁t 2 +C₁t 3 и x₂= A₂t+B₂t 2 +C₂t 3 ,где B₁=4 м/с 2 , С₁= -3 м/с 3 , B₂= -2 м/с 2 , С₂= 1 м/с 3 . Определить момент времени, для которого ускорение этих точек будут равны.

Ответ: t=0,5 с.

3.(1.5) Движение материальной точки задано уравнением x=Аt+Bt 2 , где А=4 м/с, В=–0,05 м/с 2 . Определить момент времени t, в который скорость точки u=0. Найти координату x и ускорение точки a в этот момент.

Ответ: t=40 c; x=80 м; а=–0,1 м/с 2 .

4.(1.6) Точка движется по окружности радиусом R=2 м. Уравнение движения точки j=Аt+Bt 3 , где А=1 с -1 , В=0,4 с -3 . Определить тангенциальноеa_t, нормальное a_n и полное a ускорения точки в момент времени t=2с.

Ответ: а_t=9,6 м/с 2 ; а_n=67,3 м/с 2 ; а=68,0 м/с 2 .

5.(1.9) Колесо радиусом R=0,2 м вращается так, что зависимость от времени линейной скорости точек, лежащих на ободе колеса, дается уравнением u=At+Bt 2 , где А=0,06 м/с 2 , В=0,02 м/с 3 . Найти угол a, который составляет вектор полного ускорения с радиусом колеса в моменты времени t₁=1 с, t₂=2с после начала движения.

Ответ: a₁=72,2 0 ; a₂=35 0 .

6. (1.34) Колесо вращается с постоянным угловым ускорением e= 3 рад/с 2 . Определить радиус колеса, если через t=1с после начала движения полное ускорение колеса a=7,5 м/с 2 .

Ответ: R=79 см.

7. На вал радиусом R=10 см намотана нить, к концу которой привязана гиря. Двигаясь равноускоренно, гиря за t=20 с от начала движения опустилась на h=2 м. Найти угловую скорость и угловое ускорение вала для этого момента времени.

Ответ: w=2h/(Rt)=2 рад/с; e=2h/(Rt 2 )=0,1 рад/с 2 .

8.(1.66) При выстреле пуля вылетела со скоростью u₀=200 м/с под углом a=60 0 к горизонту. Определить наибольшую высоту подъема h, дальность полета S и радиус кривизны R траектории пули в ее наивысшей точке. Сопротивлением воздуха пренебречь.

Ответ: h=1531 м; S=3535 м; R=1020 м.

9.(1.69) Тело брошено со скоростью u₀=20 м/с под углом a=30 0 к горизонту. Пренебрегая сопротивлением воздуха, найти скорость u тела, а также его нормальное a_n и тангенциальное a_t ускорения через t=1,5 с после начала движения. На какое расстояние x переместится за это время тело по горизонтали и на какой высоте yоно окажется?

Ответ: u=17,9 м/с; a_n=9,72 м/с 2 ; a_t=2,67 м/с 2 ; x=26 м; y=4 м.

10.(1.73) Электроны, обладающие кинетической энергией Е_к=1,6 кэВ, влетают посередине между пластинами плоского конденсатора параллельно им. Какое минимальное напряжение U_m необходимо подвести к пластинам, чтобы электроны не вышли за пределы пластин? Длина пластин l=2 см, расстояние между ними d=1 см
(1 кэВ=1,610 -16 Дж).

Ответ: U_m=800 В.

ЗАДАЧИ ГРУППЫ С

1. Скорость течения реки по ее ширине меняется по закону u=Ax 2 +Bх+C, где 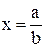(а – расстояние от берега, b – ширина реки), A=–4 м/с, B=–A, C=0,5 м/с. На какое расстояние снесет лодку течением при переправе, если скорость ее относительно стоячей воды равна u₁=2 м/с и направлена прямо к противоположному берегу? Ширина реки b=420 м.

Ответ: S=245 м.

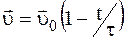
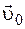
2. В момент t=0 частица вылетает из начала координат в положительном направлении оси х. Ее скорость изменяется со временем по закону , – начальная скорость, модуль которой u₀=10 см/с, t=5 с. Найти зависимость координаты частицы от времени. Рассчитать: а) координату х частицы в моменты времени 6, 10, 20 с; б) моменты времени, когда частица будет находиться на расстоянии 10 см от начала координат.

Ответ: а) x=u₀t(1–t/2t); 0,24; 0 и –4 м; б) 1,1; 9 и 11 с.

3. Радиус-вектор движущейся точки А изменяется со временем t по закону где a и b – постоянные, и – орты осей x и y. Найти: а) уравнение траектории точки; б) зависимости от времени скорости , ускорения и модули этих величин; в) зависимость от времени угла j между векторами и .

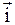
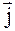
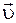
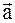
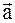
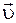
Ответ: a)

б) , a=2b;

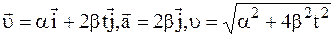
в)

4. Нормальное ускорение точки, движущейся по окружности радиусом R=4 м, изменяется по закону а_n=a+bt+ct 2 , где a, b, c – постоянные величины. Найти тангенциальное ускорение точки, путь, пройденный точкой за время t₁=6 c после начала движения, и полное
ускорение в момент времени t₂=2/3 с, если а=1 м/с 2 , b=3 м/с 3 ,
с=2,25 м/с 4 .

Ответ: а_t=3 м/с 2 , s=66 м; а=5 м/с 2 .

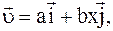
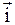
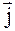
5. Частица движется в плоскости xy со скоростью где , – орты осей x и y соответственно, а и b – постоянные. В начальный момент частица находилась в точке x=y=0. Найти: a) уравнение траектории частицы y(x); б) радиус кривизны траектории в зависимости от координаты х.

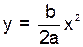
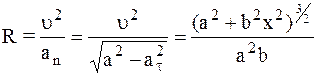
Ответ: a) ; б) .

6. Два тела бросили одновременно: одно – вертикально вверх со скоростью u₁=25 м/с, другое – под углом a=30 0 к горизонту со скоростью u₂=30 м/с. Пренебрегая сопротивлением воздуха, найти их относительную скорость во время движения.

Ответ: 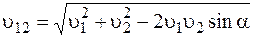=28 м/с.

7. Из пушки выпустили последовательно два снаряда со скоростью u₀=250 м/с: первый – под J₁=60 0 к горизонту, второй – под углом J₂=45 0 (азимут один и тот же). Найти интервал времени между выстрелами, при котором снаряды столкнутся друг с другом.

Ответ: 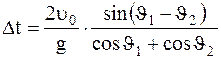=11 с.

8. Твердое тело начинает вращаться вокруг оси, неподвижной в пространстве, по закону j=аt–bt 3 , где а=6 рад/с, b=2 рад/с 3 . Найти:
а) средние значения угловой скорости и углового ускорения за промежуток времени от t=0 до остановки; б) угловое ускорение в момент остановки тела.

Ответ: a) =2а/3=4 рад/с; б) = 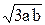=6 рад/с 2 .

9. При вращении махового колеса его угловое ускорение изменяется по закону e= — abw, а и b – постоянные. Найти: а) чему равна угловая скорость маховика через t_c после начала притормаживания, если в момент t=0 она была равна w₀? б) какой вид движения у маховика при t® ¥? в) как зависит от времени его угловое ускорение?

Ответ:

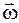
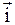
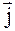
10. Твердое тело вращается с угловой скоростью =At +Bt 2 , где А=0,5 рад/с 2 , В=0,06 рад/с 3 . Найти для момента t=10 с: а) модули угловой скорости и углового ускорения; б) угол между этими векторами.

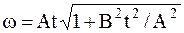
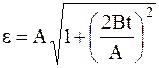
Ответ: а) =8 рад/с; =1,3 рад/с; б) 17 0 .

Видео:Кинематика материальной точки за 20 минут (кратко и доступно) Кинематика точкиСкачать

Динамика материальной точки. Кинематика материальной точки

Кинематика материальной точки

1. Вектора. Запись векторов в декартовой системе координат. Модуль вектора.

2. Радиус-вектор. Запись радиус-вектора в Декартовых координатах.

3. Вектор скорости. Движение по инерции.

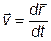
Пример:
Материальная точка, двигаясь равномерно и прямолинейно со скоростью V=5e_x+2e_y+7e_z (м/с), На каком расстоянии от начала координат на расстоянии (в м) находится точка через 10с.

Скорость материальной точки задана уравнением v = 2e_x +1e_y+6 e_z (м/c). Движение точки является равномерным, равноускоренным, равнозамедленным, с возрастающим ускорением или с убывающим ускорением?

Положение материальной точки задано уравнением r = 5t e_x+ 1t 2 e_y+ 0.5t 3 e_z (м). Найти мгновенную скорость точки (в м/с) через 5с после начала движения.

4. Перемещение

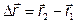
Пример:
Положение материальной точки задано уравнением r= 1te_x+ 3t 2 e_y+ 0.5t 3 e_z (м). Найти перемещение (в м) за пятую секунду и модуль этого перемещения.

5. Траектория движения тела

Положение материальной точки задано уравнением r = 10t 2 e_x+ 7e_y+ 6t e_z (м). Записать уравнение траектории движения тела.

6. Вектор ускорения.

Положение материальной точки задано уравнениемr =3t 2 e_x+ 2t 2 e_y+ t 2 e_z (м). Найти вектор ускорения тела (в м/с 2 ) .

7. Типы движения. Равномерное, равноускоренное, равнозамедленное.

8. Нормальное и тангенциальное ускорения.
a_n=v 2 /R;

Материальная точка движется по окружности радиуса R= 20 см со скоростью V= 6t (м/с). Найти тангенциальное ускорение точки (в м/с 2 ) через 2 с от начала движения.

Материальная точка движется по окружности радиуса R=2 см со скоростью V=5м/с. Найти нормальное ускорение точки (в м/с 2 ).

9. Угловая скорость, Угловое ускорение.

Пример
Тело равномерно вращается по окружности радиуса 10 см с угловой скоростью ω=10 рад/с. Найти угловое ускорение (в рад/с 2 ):

10. Частота вращения, Число оборотов

Тело, равномерно вращается с угловой скоростью ω = 9.42 рад/с. Какова частота вращения (в об/с).

11. Уравнение кинематики равнопеременного вращательного движения

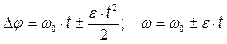
Пример 1:

Тело, вращаясь равнозамедленно, за 10 секунды изменило угловую скорость от ω₁= 6 рад/с до ω₂ = 1 рад/с. Найти угловое ускорение тела (в рад/с 2 ) .

Тело, вращаясь равноускоренно, за 10с от начала движения совершило 30 оборотов. Найти угловое ускорение тела (в рад/с 2 ).

Колесо радиусом 1м вращается согласно уравнению φ = 2-4t+0,1t 2 . Чему равна частота вращения колеса через t = 2с от начала отсчета времени.

Динамика материальной точки

Сила. Нормальная и тангенциальная составляющие силы при криволинейном движении.

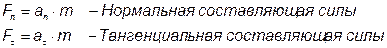
Пример:

Материальная точка массой 1 кг движется по окружности радиуса 1 м с возрастающей скоростью V= 3t (м/с). Найти нормальную составляющую силы, действующей на тело через 2 с от начала движения (в Н).

Центр масс системы материальных точек

Найти координаты центра масс системы частиц с массами m₁ = 15 кг и m₂ = 20 кг, изображенной на рисунке.

Импульс материальной точки

Импульс системы материальных точек

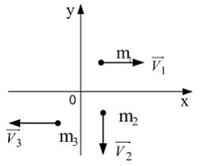
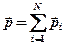
Пример:
Система состоит из трех шаров с массами , , , которые движутся так, как показано на рисунке.
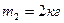
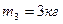
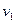
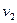
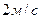
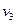
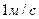
Cкорости шаров равны : = , = , = . Как направлен вектор импульса центра масс.

Второй закон Ньютона.

Материальная точка (тело массой 4 кг ) движется по окружности радиуса R= 2 см с возрастающей скоростью V= 2t (м/с). Найти тангенциальную составляющая силы, действующей на тело через 3 с от начала движения.

Тело массой 1 кг движется с ускорением 3 м/с 2 . Найти силу, действующую на тело.

Под действием результирующей силы 10Н у тела изменился импульс на 0.2 кг м/с. Найти время действия силы.

Скорость тела массой m = 1 кг изменяется по закону V = 1t e_x+3t 2 e_y+0.3t 3 e_z (м/с). Найти модуль действующей силы через 1с от начала движения (в Н).

При взлете самолета пилот испытывает 2-кратные перегрузки. Найти ускорение самолета (в м/с 2 ).

Сила трения скольжения

Если коэффициент трения μ= 0,01 , то на тело массой m = 10 кг, движущееся по наклонной плоскости под углом 20 о к горизонту, действует сила трения

Сила Гравитации(Всемирного тяготения). Ускорение свободного падения(связь с законом всемирного тяготения)

Ускорение свободного падения на поверхности планеты:

Найти ускорение свободного падения на планете, масса которой в 3 раза меньше , чем у Земли, а радиус в 2 раза больше.

Сила натяжения подвеса. Вес тела.

Пример:
К нити подвешен груз массой 10 кг. Нить с грузом опускается с ускорением 5м/с 2 . Найти силу натяжения нити (в Н).

Силы вязкого трения.

Закон сохранения импульса

При выстреле из ружья массой 5 кг пуля массой 10 г летит со скоростью 600 м/с. Найти скорость отдачи ружья.

Катер, двигаясь со скоростью меньше критической, стал двигаться быстрее в 2 раза. Во сколько раз возросла сила сопротивления?

Пример:
Автомобиль массой 2т едет со скоростью 60 км/час по горизонтальной дороге. Коэффициент трения колес о дорогу μ = 0,5. Найти мощность двигателя (в кВт).

Инерциальная система отсчета.

Положения трёх тел относительно звезд изменяются по законам: 1) r₁=3t e_x+4t e_y+1t e_z(м), 2) r₂=2t 2 e_x +2t e_y +5t 3 e_z(м), 3) r₃ = 6 e_x + 5 e_y + 1 e_z (м). Системы отсчета, связанные с какими телами, являются инерциальными?

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Уравнение движения материальной точки

Движение материальной точки в пространстве – это изменение ее положения относительно других тел с течением времени.

Имеет смысл говорить только о движении в некоторой системе отсчета.

Видео:К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать

Система отсчета. Системы координат

Точки, располагаемые в пустом пространстве, не различаются. Поэтому о точке рассуждают при условии нахождения в ней материальной точки. Определить ее положение можно при помощи измерений в системе координат, где и проводится нахождение пространственных координат. Если рассматривать в виде примера поверхность Земли, то следует учитывать широту и долготу располагаемой точки.

В теории используется декартова прямоугольная система координат, где определение точки возможно при наличии радиус-вектора r и трех проекций x , y , z – ее координат. Могут быть применены другие:

• сферическая система с положением точек и ее радиус-вектором, определенных координатами r , υ , φ ;
• цилиндрическая система с координатами p , z , α ;
• на полярной плоскости с параметрами r , φ .

В теории зачастую не принимают во внимание реальную систему отсчета, а сохраняют только ту, которая представляет собой ее математическую модель, применяемую во время практических измерений.

Видео:Дифференциальное уравнение движения материальной точки.Скачать

Кинематическое уравнение движения материальной точки

Любая система отсчета или координат предполагает определение координат материальной точки в любой момент времени.

При условии положения и определения материальной точки в данной системе отсчета считается, что ее движение задано или описано.

Это возможно при использовании кинематического уравнения движения:

Аналитически положение точки определяется совокупностью трех независимых между собой чисел. Иначе говоря, свободная точка имеет три степени свободы движения.

Ее перемещение по уравнению ( 1 ) определено, если имеется указанное положение в любой момент времени t . Для этого следует задавать декартовы координаты точки в качестве однозначных и непрерывных функций времени:

x ( t ) = x , y ( t ) = y , z ( t ) = z ( 2 ) .

Прямоугольные декартовы координаты x , y , z — это проекции радиус-вектора r ¯ , проведенного из начала координат. Очевидно, что длину и направление r ¯ можно найти из соотношений, где a , β , γ являются образованными радиус-вектором углами с координатными осями.

Равенства ( 2 ) считают кинематическими уравнениями движения материальной точки в декартовых координатах.

Они могут быть записаны в другой системе координат, которая связана с декартовой взаимно однозначным преобразованием. Если движение точки происходит в плоскости О х у , тогда применимы полярные координаты r , φ , относящиеся к декартовым преобразованиям. Данный случай подразумевает использование уравнения движения точки следующего вида:

r = r ( t ) , φ = φ ( t ) ( 3 ) .

Кинематическое уравнение движения точки в криволинейных координатах q 1 , q 2 , q 3 , связанных с декартовыми преобразованиями вида x = x ( q 1 , q 2 , q 3 ) , y = y ( q 1 , q 2 , q 3 ) , z = z ( q 1 , q 2 , q 3 ) ( 4 ) , записывается как

q 1 = q 1 ( t ) , q 2 = q 2 ( t ) , q 3 = q 3 ( t ) ( 5 ) .

Кривая радиус-вектора, описываемая концом вектора r при движении точки, совпадает с ее траекторией. Параметрическое уравнение траектории с t представлено кинематическими уравнениями ( 2 ) , ( 5 ) . Чтобы получить координатное уравнение траектории следует исключить время из кинематических уравнений.

Определение движения точки возможно с помощью задания траектории и мгновенного положения точки на ней. Ее положение на кривой определяется с помощью указания только одной величины: расстояния вдоль кривой от некоторой начальной точки с положительным направлением:

Это и есть уравнение движения точки по траектории. Способ его задания относят к естественному или траекторному.

Понятия координатного и естественного способа задания движения точки физически эквивалентны. С математической стороны это рассматривают как возможность применения разных методов, исходя из случая математической задачи.

Задание такого закона возможно аналитическим, графическим путем или с использованием таблицы, последние два из которых зачастую рассматривают в виде графиков и расписаний движений поездов.

Дано уравнение движения материальной точки x = 0 , 4 t 2 . Произвести запись формулы зависимости υ x ( t ) , построить график зависимости скорости от времени. На графике отметить площадь, численно равную пути, пройденному точкой за 4 секунды, произвести вычисление.

Дано: x = 0 , 4 t 2 , t = 4 c

Найти: υ x ( t ) , S — ?

Решение

При решении необходимо учитывать зависимость скорости от времени:

υ x = υ 0 x + a x t .

Зависимость координаты от времени и сравнение уравнения с заданным принимает вид:

x = x 0 + υ 0 x t + a x t 2 2 , x = 0 , 4 t 2 .

Очевидно, что x 0 = 0 , υ 0 x = 0 , a x = 0 , 8 м / с 2 .

После подстановки данных в уравнение:

Определим точки, изобразим график:

υ x = 0 , t = 0 , υ x = 4 , t = 5

Путь, по которому двигалось тело, равняется площади фигуры, ограниченной графиком, и находится с помощью формулы:

📸 Видео

Кинематика точки Задание К1Скачать

Кинематика точки. Авторы: Борисов Никита, Ларионов Егор, Петрашова Полина. Решение задачи.Скачать

Урок 7. Механическое движение. Основные определения кинематики.Скачать

Лекция №1 "Кинематика материальной точки" (Булыгин В.С.)Скачать

Прямолинейные колебания материальной точкиСкачать

Лекция 01 Кинематика материальной точкиСкачать

ЕГЭ по математике. Профильный уровень. Задание 7. Закон движения. ПроизводнаяСкачать

Физика 10 класс (Урок№2 - Равномерное прямолинейное движение материальной точки.)Скачать

Д1 Дифференциальные уравнения движения материальной точкиСкачать

Консультация к устному экзамену. Механика. Часть 1: "Движение материальной точки"Скачать

Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Механика || Кинематика материальной точки (Часть 1)Скачать

Решение графических задач на равномерное движениеСкачать

Теоретическая механика. Задание К1 (часть 1) из сборника ЯблонскогоСкачать

ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.Скачать

Материальная точка. Система отсчета | Физика 9 класс #1 | ИнфоурокСкачать