Планирование работы эксперимента. Различают активный и пассивный эксперимент. Пассивный – это сбор статистического материала в ходе эксплуатации оборудования, либо эксперимента с поочередным варьированием факторов. Различают несколько планов эксперимента. Один из основных – это полный фактор эксперимента (ПФЭ).
П.Ф.Э. – такое планирование эксперимента, при котором реализуются все сочетания из k факторов на выбранных уровнях.
Уровни – отдельные значения факторов, при которых проводится эксперимент.
При планировании эксперимента факторы приводятся к безразмерному виду.
Пусть требуется исследовать связь между выходом продукта в зависимости от 3-х факторов:
Z1 – температура, Z2 – давление, Z3 – время пребывания;



100, 200 – уровни исследования
Эксперимент проводится только на границах: на 2-х уровнях
Определяется ср. знач. интервала:
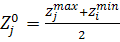
Точка 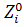
Определяется значение подинтервала (100,150), (150,200):
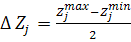
j – номер фактора
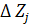
Переводим к безразмерному виду фактор 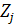
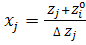
В центре плана все факторы = 0
На верхней границе исследования значения всех безразмерных факторов = +1, на нижней границе = -1.
После этого приступают к планированию эксперимента.
Количество опытов в П.Ф.Э. : N=q k (q – число уровней, k- количество факторов)
q=2 (опыты ставятся на верх или нижн границе)
План эксперимента (матрица эксперимента):
| № | x0 | x1 | x2 | x3 | x1 x2 | x1 x3 | x2 x3 | x1 x2 x3 | y |
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | y1 | |
| +1 | +1 | -1 | +1 | -1 | -1 | -1 | -1 | y2 | |
| +1 | -1 | +1 | +1 | -1 | -1 | +1 | -1 | y3 | |
| +1 | -1 | -1 | +1 | +1 | +1 | -1 | +1 | y4 | |
| +1 | +1 | +1 | -1 | +1 | +1 | -1 | -1 | y5 | |
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | y6 | |
| +1 | -1 | +1 | -1 | -1 | -1 | -1 | +1 | y7 | |
| +1 | -1 | -1 | -1 | +1 | +1 | +1 | -1 | y8 |
Это свойство называется свойством ортогональности
3. 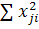
N – число опытов
П.Ф.Э. позволяет описать область исследования уравнением регрессии, которое включает в себя как линейные эффекты, так и эффекты взаимодействия. То есть в случае 3-х факторов уравнение регрессии будет иметь след. Вид:
b1, b2, b3 – линейные эффекты, остальные – эффекты взаимодействия.
Этот план можно использовать, если объект удовлетворяет уравнению (7), (если есть квадратичные эффекты, то ПФЭ не подходит)
Поставили эксперимент, получили y1…y8.
Нужно рассчитать коэффициенты исходя из матричного уравнения (X T X)B=(X T Y)
 | 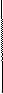 |
X T X=
Диагональные эксперименты – квадраты ( 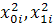
По свойствам 1,3 :




 |  |
X T Y =
bj = 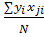
Исходя из (8) вытекает:
1. Коэффициенты регрессии рассчитываются независимо друг от друга по формуле (8)
2. Коэффициенты регрессии не коррелированны между собой, а это значит, что они являются несмешанными оценками соответствующих генеральных коэффициентов.
bj 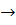
(bj учитывают только фактор xj)
Пусть y1…y8 = 1…8 соответственно
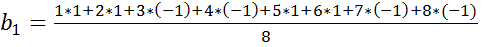
x0 – фиктивная переменная
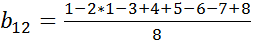
Так как коэффициенты регрессии не коррелированны , критерий Стьюдента рассчитывается отдельно для каждого коэффициента
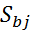
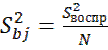
Матрица планирования обладает также свойством рототабельности.
Ошибка уравнения в соответствии с законом накопленных ошибок рассчитывается по формуле:
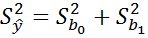
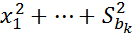
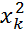
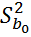
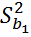
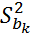
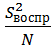
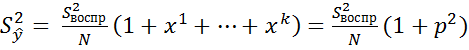
p – радиус сферы в k-мерном пространстве из (12) вытекает:
1. Ошибка ур-я увел-ся с увел-ем радиуса сферы.
2. Ошибка ур-я для эквидистантных точек, находящихся на поверхности сферы радиуса p одинаковы.
Это свойство рототабельности.
Обработка ПФЭ состоит из 3-х основных этапов:
1. Расчет коэффициентов регрессии.
2. При наличии параллельных опытов оценка значимости коэффициентов по кр. Стьюдента по сравнению с ошибкой эксперимента.
3. Проверка адекватности уравнения по кр. Фишера.
Динамические модели, временная и операторная формы представления моделей.
Видео:Выбор факторов, влияющих на результативный показательСкачать

Полный факторный эксперимент и уравнение регрессии
Перечисленные два этапа построения многофакторных моделей на практике часто решаются с помощью методики ПФЭ типа 2k. Применение этой методики позволяет достаточно просто и эффективно количественно оценить все линейные эффекты факторов и их взаимодействия («перекрестные связи»). взаимодействие возникает в том случае, если эффект одного фактора зависит от уровня, на котором находится другой фактор. Вначале рассмотрим методику получения линейной РМ.
Линейная регрессионная модель. Уравнение регрессии – это формула статистической связи между зависимыми и независимыми переменными. Если это уравнение линейное, то речь идет о линейной регрессии. Формула статистической связи двух переменных называется парной регрессией, зависимость от нескольких переменных – множественной регрессией. Например, Кейнсом была предложена линейная формула зависимости частного потребления С от располагаемого дохода 



Установление формы связи (9.2.1) начинают, как правило, с рассмотрения линейной регрессии вида

Целью исследователя является определение неизвестных коэффициентов 

Используя для этого метод наименьших квадратов (МНК) для линейной РМ получим простую формулу

где индекс 


Пример.подсчитаем коэффициенты для линейной двухфакторной РМ

Для этого воспользуемся значениями 
Коэффициент 

Нелинейная регрессионная модель.Если при проверке гипотезы о линейности РМ устанавливается, что статистический материал (или результат ПФЭ) не может быть описан линейным уравнением, то переходят к поиску нелинейной модели. Как уже указывалось, структура нелинейной РМ может быть совершенно различной. Пользуясь результатами ПФЭ можно достаточно просто построить нелинейную модель, включающую эффекты взаимодействия («перекрестные связи») факторов: парные ( 

Максимальное число всех возможных эффектов (всех членов уравнения регрессии, включая 

где k – число факторов, m – число элементов во взаимодействии, N – количество опытов в эксперименте (число строк в матрице планирования ПФЭ).
Пример.для ПФЭ 2 4 число возможных парных взаимодействий равно шести:
Для определения коэффициентов в модели при парных взаимодействиях надо, пользуясь правилом перемножения столбцов, получить столбец произведения двух факторов. Для вычисления коэффициента при соответствующем эффекте взаимодействия, с новым вектор-столбцом можно обращаться так же, как с вектор-столбцом любого фактора.
В табл.13 представлена матрица планирования ПФЭ типа 2 2 с учетом перекрестных связей между факторами.
Т а б л и ц а 13
| Номер опыта |  | 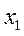 |  |  | y |
| +1 +1 +1 +1 | +1 –1 +1 –1 | +1 +1 –1 –1 | +1 –1 –1 +1 | y1 y2 y3 y4 |
Полная нелинейная РМ в данном случае имеет следующий вид:


Коэффициент 


Для определения коэффициентов в модели при тройных взаимодействиях и взаимодействиях более высокого порядка поступают аналогично. В табл.14 приведены условия проведения ПФЭ типа 2 3 и дополнительные столбцы для расчета коэффициентов в перекрестных связях. Полная нелинейная РМ с учетом всех возможных взаимодействий в этом случае имеет вид:


Коэффициент 


Т а б л и ц а 14
| Номер опыта |  | 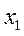 |  |  |  |  |  |  | y |
| +1 +1 +1 +1 +1 +1 +1 +1 | +1 –1 +1 –1 +1 –1 +1 –1 | +1 +1 –1 –1 +1 +1 –1 –1 | +1 +1 +1 +1 –1 –1 –1 –1 | +1 –1 –1 +1 +1 –1 –1 +1 | +1 –1 +1 –1 –1 +1 –1 +1 | +1 +1 –1 –1 –1 –1 +1 +1 | +1 –1 –1 +1 –1 +1 +1 –1 | y1 y2 y3 y4 y5 y6 y7 y8 |
Метод наименьших квадратов.Метод наименьших квадратов (МНК), или Least Squares Method (LS), это наиболее распространенный метод вычисления коэффициентов регрессионной модели. Как уже отмечалось, вычисление коэффициентов РМ с использованием матрицы планирования ПФЭ накладывает существенные ограничения на структуру РМ и является частным случаем МНК.
МНК минимизирует сумму квадратов отклонений наблюдений зависимой переменной от искомого уравнения регрессии (РМ). Рассмотрим суть метода на примере определения коэффициентов однофакторной линейной регрессионной модели

Для вычисления неизвестных коэффициентов 





где 


 |
|
 |
Требуется найти такие коэффициенты регрессии (9.4.8), при которых невязки будут минимальными.
В МНК коэффициенты находят из условия минимума функции V

Подставив (9.4.9) в (9.4.10), получим:


Минимум функции, если он существует, достигается при одновременном равенстве нулю частных производных по всем неизвестным, т.е.

Из выражений (9.4.11) и (9.4.12) получим систему уравнений для определения искомых коэффициентов РМ (9.4.8):

Решение системы (9.4.13) значительно упрощается, если использовать рассмотренные ранее свойства ПФЭ (9.2.6) – (9.2.8). В этом случае

Обобщая результат для любого количества факторов, можно записать общую формулу расчета коэффициентов множественной линейной регрессии для ПФЭ типа 
Эту формулу мы уже использовали для определения коэффициентов РМ с помощью матрицы планирования ПФЭ.
Чтобы формально можно было решить поставленную задачу, то есть найти некоторый наилучший вектор параметров РМ, должно выполняться неравенство 

Можно показать, что система нормальных уравнений (9.4.12) МНК в матричном виде записывается следующим образом:

где 


где 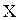
Проверка адекватности модели.После выбора структуры и вычисления коэффициентов регрессионной модели (РМ) встает вопрос о степени ее адекватности, т.е. о степени ее соответствия исследуемой системе. При проверке с помощью методов регрессионного анализа гипотезы об адекватности модели или о значимости входящих в РМ коэффициентов, приходится учитывать законы распределения случайных параметров.
регрессионный анализ применим при следующих предположениях.
1. Параметр оптимизации у есть случайная величина с нормальным законом распределения.
2. Дисперсия 
3. Значения факторов xj суть неслучайные величины.
Если в рассматриваемой задаче выполняются все предположения, то можно проверять статистические гипотезы.
Для проверки гипотезы об адекватности модели можно использовать критерий Фишера (этот критерий мы уже использовали для проверки однородности дисперсий):
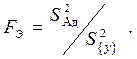
Здесь 

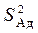

где 

Если рассчитанное значение критерия не превышает табличного ( 
В случае если опыты в матрице планирования дублируются, то дисперсия адекватности рассчитывается по формуле

где ni – число параллельных опытов в i —ой строке матрицы планирования; 


Для определения коэффициентов 
Пример.В табл.15 приведена матрица планирования ПФЭ типа 2 2 с двумя параллельными опытами в каждой строке. Во втором опыте один из параллельных опытов пришлось отбросить как грубый.
При двух параллельных опытах со значениями 


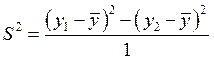
| № | 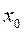 |  |  |  |  |  |  | 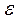 |  |  |  |  |
| +1 +1 +1 +1 | –1 +1 –1 +1 | –1 –1 +1 +1 | 4,5 3,0 2,0 0,5 | 5,5 — 2,0 1,5 | 5,0 3,0 2,0 1,0 | 4,75 3,25 2,25 0,75 | 0,25 -0,25 -0,25 0,25 | 0,0625 0,0625 0,0625 0,0625 | 0,125 0,0625 0,125 0,125 | 0,5 — 0,5 |
Т а б л и ц а 15
Зададимся начальной структурой регрессионной модели (РМ) в линейной форме
По результатам ПФЭ требуется определить коэффициенты РМ и доказать, что принятая модель адекватна.
Используя свойства и методику определения коэффициентов РМ с помощью матрицы планирования, по формуле (9.4.2) подсчитаем значения коэффициентов РМ.
Итак, мы получили линейную РМ:
Проверим адекватность этой модели. Вспомогательные расчеты представлены в последних шести столбцах табл.15.
Рассчитываем дисперсию воспроизводимости по формуле (9.2.13) с тремя степенями свободы:
Рассчитываем дисперсию адекватности по формуле (9.4.18) с одной степенью свободы:
Экспериментальное значение критерия Фишера рассчитаем по формуле (9.4.17): 
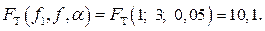

Методы упрощения уравнения регрессии.При построении РМ для целевой функции у на начальном этапе обычно стараются учесть как можно большее число факторов, влияющих на изменение у. В этом случае часто получаются неоправданно сложные модели, особенно при использовании нелинейных форм. эти модели можно значительно упростить, если выявить те факторы, которые незначительно влияют на функцию отклика, и исключить эти факторы из уравнения регрессии.
При отборе влияющих факторов используются статистические методы отбора. Так, существенного сокращения числа влияющих факторов можно достичь с помощью пошаговых процедур отбора переменных. Ни одна их этих процедур не гарантирует получения оптимального набора переменных. Однако при практическом применении они позволяют получить достаточно хорошие наборы существенно влияющих факторов.
Для анализа РМ с целью упрощения используются несколько методов. Коротко рассмотрим некоторые из них.
1. Метод всех регрессий. В этом методе функцию отклика представляют в виде комбинаций зависимостей, в которых меняют число факторов. Так для уравнения регрессии
можно записать функцию отклика в различных комбинациях:
Для каждого уравнения вычисляются коэффициенты регрессии и определяется дисперсия адекватности 
2. Метод исключения переменных. Метод исключения предполагает построение РМ, включающей всю совокупность переменных, с последующим последовательным (пошаговым) сокращением числа переменных в модели до тех пор, пока не выполнится некоторое, наперед заданное, условие.
После построения РМ с целью сокращения членов в уравнении РМ и ее упрощения зачастую различными способами проводят оценку значимости коэффициентов модели. оценку значимости можно осуществить с помощью t-критерия Стьюдента.
При проверке значимости коэффициентов 




Вычисленное значение 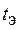


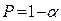
3. Метод включения переменных. Суть метода включения состоит в последовательном включении переменных в модель до тех пор, пока регрессионная модель не будет отвечать заранее установленному критерию качества. Последовательность включения определяется с помощью частных коэффициентов корреляции: переменные, имеющие относительно исследуемого показателя большие значения частного коэффициента корреляции, первыми включаются в регрессионное уравнение.
4. Метод анализа невязок состоит в том, что анализируется разница между значениями функции 

проверяют их среднее значение, которое должно быть близким к нулю:
Если это условие не выполняется, то в уравнение модели вносят дополнительные члены или принимают другую структуру РМ.
В 30-е гг. ХХ века повсеместное увлечение множественной регрессией сменилось разочарованием. Строя уравнение множественной регрессии и, стремясь включить как можно больше объясняющих переменных, исследователи все чаще сталкивались с бессмысленными результатами. Причина заключалась в том, что изолированно взятое уравнение регрессии есть не что иное, как модель «черного ящика», поскольку в ней не раскрыт механизм зависимости выходной переменной Y от входных переменных Хi , а лишь констатируется факт наличия такой зависимости.
Для проведения правильного анализа нужно знать всю совокупность связей между переменными. Одним из первых подходов к решению этой задачи является конфлюэнтный анализ, разработанный в 1934 г. Р.Фришем. Он предложил изучать иерархию регрессий между всеми сочетаниями переменных.
Значительный интерес представляет аналитический метод выбора типа уравнения регрессии, который основан на изучении материальной природы связи исследуемых признаков.
[1] Интеркорреляция – корреляция между объясняющими переменными.
Видео:Планирование и оптимизация экспериментаСкачать

Лекция 7 Введение в теорию Промышленного Эксперимента
| Название | Лекция 7 Введение в теорию Промышленного Эксперимента |
| Дата | 02.12.2020 |
| Размер | 1.77 Mb. |
| Формат файла |  |
| Имя файла | vse_lektsii_v_odnom_fayle.docx |
| Тип | Лекция #156246 |
| страница | 4 из 9 |
| Подборка по базе: 9 Лекция.pdf, №1 Введение.pdf, Логопсихология_ Введение в логопсихологию лекция.ppt, 1 лекция голова шея-1.docx, НУПЗиПИУ. Модуль 2. Лекция 2.docx, Хадур Мажд — 359А — лекция 1.docx, 1. Лекция Особенности макетирования и верстки длинных документов, Медицинская статистика Лекция проф.Виноградова К.А.(1).pptx, 6 лекция Отбасы.ppt, 9-10 Лекция дуниетану.ppt Линейное уравнение регрессии не всегда обеспечивает достаточную адекватность получаемой модели. В то же время подавляющее большинство объектов могут быть описаны с достаточной точностью уравнения регресии в виде полинома второго порядка:
Экспериментальные наблюдения за независимыми переменными образно можно представить как лежащие в вершинах n-мерного гиперкуба, вписанного в сферу с радиусом , n – количество опытов, которые нужно включить в матрицу планов. Если рассмотреть планирование двухфакторного эксперимента, то на осях координат x1 и x2 гиперкуб может быть представлен в виде квадрата с вершинами 1, 2, 3, 4, вписанного в сферу. Представим матрицу полного двухфакторного эксперимента, в которую желательно включить и коэффициенты при квадратах независимых переменных (табл.3.9).
В матрице плана нарушено свойство ортогональности между z0, Можно увеличить количество факторов, но тогда оно будет катастрофически возрастать. Выходом из этой ситуации является использование в матрице планов при двухуровневом планировании центральной точки с координатами (0,0. 0) и так называемых звездных точек. Координаты звездных точек определяются как (0,0. + ,– . 0,0), т. е. как нулевые для всех остальных переменных, за исключением одной, которая может принимать значение, равное со знаками « +» и «–». Таким образом, к нашей матрице планов кроме основных четырех опытов добавится еще пять (табл.3.10), где опыты 9 – центральные точки (nц).
Можно определить общее количество опытов (n), которые будут состоять из количества опытов ПФЭ (nпфэ), количества звездных точек (nзв) и количества центральных точек (nц):
Рассмотренные значения не приведут к ортогональности матрицы. Чтобы привести матрицу к отрогональному виду, необходимо преобразование столбцов соответствующих квадратов независимых переменных. Преобразование заключается в следующем:
Значение зависит от количества независимых переменных k: при k=2 = 1, при k=3 = 1,215, при k=4 = 1,414 [25]. С учетом преобразования получим ортогональную матрицу плана: при k=2, = 1, С 2 =4/9, С0,67 (табл. 3.11).
Уравнение регрессии выглядит следующим образом: Вычисление коэффициентов уравнения bi и проверка адекватности модели аналогична ПФЭ. Дробный факторный эксперимент Количество опытов в полном факторном эксперименте значительно превосходит число определяемых коэффициентов линейной модели. Другими словами, полный факторный эксперимент обладает большой избыточностью опытов. Было бы заманчивым сократить их число за счет той информации, которая не очень существенна при построении линейных моделей. При этом нужно стремиться, чтобы матрица планирования не лишилась своих оптимальных свойств. Сделать это не так просто, но все же возможно. Итак, начнем поиск путей минимизации опытов. Минимизация числа опытов Начнем с самого простого – полного факторного эксперимента 2 k . Запишем еще раз матрицу планирования
Пользуясь таким планированием, можно вычислить четыре коэффициента и представить результаты эксперт в виде неполного квадратного уравнения Если имеются основания считать, что в выбранных интервалах варьирования процесс может быть описан линейной моделью, то достаточно определить три коэффициента: b0, b1и b2. Остается одна степень свободы. Употребим ее для минимизации числа опытов. При линейном приближении и вектор-столбец x1x2 можно использовать для нового фактора x3. Поставим этот фактор в скобках над взаимодействием x1x2 и посмотрим, каковы будут оценки коэффициентов. Здесь уже не будет тех раздельных оценок, которые мы имели в полном факторном эксперименте 2 k . Оценки смешаются следующим образом: Но нас это не должно огорчать. Ведь мы постулируем линейную модель, и, следовательно, все парные взаимодействия незначимы. Главное, мы нашли средство минимизировать число опытов: вместо 8 опытов для изучения трех факторов оказывается можно поставить четыре! При этом матрица планирования не теряет своих оптимальных свойств (ортогональность, ротатабельность и т.п.). Найденное правило можно сформулировать так: чтобы сократить число опытов, нужно новому фактору присвоить вектор-столбец матрицы, принадлежащий взаимодействию, которым можно пренебречь. Тогда значение нового фактора в условиях опытов определяется знаками этого столбца. Поставив четыре опыта для оценки влияния трех факторов, мы воспользовались половиной полного факторного эксперимента 2 3 или «полурепликой». Если бы мы х3 приравняли к –x1x2, то получили бы вторую половину матрицы 2 3 . В этом случае , , . При реализации обеих полуреплик можно получить раздельные оценки для линейных эффектов и эффектов взаимодействия, как и в полном факторном эксперименте 2 3 . Объединение этихдвух полуреплик и есть полный факторный эксперимент 2 3 . Матрица из восьми опытов для четырех факторного планирования будет полурепликой от полного факторного эксперимента 2 4 , а для пятифакторного планирования – четверть-репликой от 2 5 . В последнем случае два линейных эффекта приравниваются к эффектам взаимодействия. Для обозначения дробных реплик, в которых p линейных эффектов приравнены к эффектам взаимодействия, удобно пользоваться условным обозначением 2 k — p . Так, полуреплика от 2 3 запишется в виде 2 3-1 а четвертьреплика от 2 5 – в виде 2 5-2 . эксперимента в условиях временного дрейфа Можно заметить, что с увеличением факторов растет число опытов в матрице плана эксперимента. Это количество можно уменьшить, если при планировании использовать дробные реплики. Если заменяется один фактор, тогда исполнительная часть матрицы составляет 1/2 от матрицы ПФЭ (n = 2 k –1 ), если заменяются два фактора – 1/4 от ПФЭ (n = 2 k –2 ), если заменяются три фактора – 1/8 от ПФЭ (n = 2 k –3 ). Допустим, нужно получить коэффициенты линейной модели в трехфакторном эксперименте, используя при этом четыре опыта вместо восьми. Тогда необходимо ввести одну так называемую дробную реплику. Введение реплики обеспечивается генерирующим соотношением. Эффект z3 может быть заменен эффектом парного взаимодействия z1·z2. Это возможно, если мы хотим ограничиться линейной моделью и предполагаем, что для исследуемого объекта влияние этих двух факторов несущественно. При этом найденный нами коэффициент уравнения регрессии будет отражать суммарное влияние фактора 3 и парного взаимодействия факторов 1 и 2: Неточность этого эксперимента есть результат платы за уменьшение количества опытов. Основные идеи дробного факторного эксперимента используются при планировании в условиях временного дрейфа, который представляет собой изменение наблюдаемой величины с течением времени, не зависящее от факторов, которыми мы варьируем. Это объясняется тем, что в реальных условиях на исследуемую переменную у оказывают влияние неуправляемые факторы, такие как колебания состава сырья, изменение внешней нагрузки, старение оборудования и т.д. Действие их вызывает нестационарное изменение у, называемое временным дрейфом у. Обычно предполагают, что дрейф не взаимодействует с факторами xi, варьируемыми в эксперименте. Такой дрейф можно интерпретировать как смещение математической модели. При экспериментировании на таком объекте выход его представляет сумму функции отклика, временного дрейфа и некоторого шума с нулевым средним и ограниченной дисперсией:
Сам дрейф – изменение выходного параметра при постоянных значениях факторов xi = constможет быть представлен в виде дискретного процесса или некоторой непрерывной функции времени. Рассмотрим наиболее простой характерный случай описания временного дрейфа линейной зависимостью. Влияние такого дрейфа на параметры математической модели можно практически устранить, разбивая серию опытов на отдельные блоки так, чтобы эффект от временного дрейфа оказался смешанным с произведениями факторов, для которых коэффициенты регрессии достаточно малы. Такое планирование эксперимента будет ортогональным к линейному дрейфу. Допустим, необходимо устранить влияние временного дрейфа на параметры уравнения регрессии, полученного в результате ПФЭ 2 3 (например, исследование эффекта вложения средств в рекламу в условиях инфляции). С этой целью разобьем матрицу планирования на два блока и введем новую независимую переменную zд, характеризующую дрейф. Положим
Количество плюсов и минусов в каждом столбце должно быть одинаково это свойство ортогональности матрицы. Уравнение регрессии имеет вид Можно доказать, что коэффициенты регрессии являются следующими оценками b: Таким образом, введенная переменная исключается в оценке коэффициента b1, т.к. суммируется одинаковое количество этих переменных со знаками плюс и минус. Аналогично вычисляются оценки коэффициентов b1, b2, b3, b12 , b23 , b13. В коэффициенте b123, определяющем взаимное влияние трех факторов, будет участвовать во всех восьми опытах со знаком плюс. Таким образом, этот коэффициент связан с влиянием факторов. Если в регрессионной модели мы пренебрегаем этим коэффициентом, то остальные коэффициенты мы получим независимо от дрейфа при проведении опытов в фиксированные моменты времени ti, для которых y=yi – yi-1= const. В случае, когда дрейф представляет более нелинейную функцию времени, то ее можно свести к линейной зависимости соответствующими преобразованиями. Задача планирования и обработка результатов эксперимента сводятся к следующему: 1. Определение величины интервала t и последовательности во времени проведения опытов t1 ,t2 ,…,tn. t должно быть таким, чтобы составляющая дрейфа от опыта к опыту изменялась на одну и ту же величину y = const. 2. Выявление влияющих факторов xi и построение матрицы плана. 3. Проведение эксперимента в соответствии с матрицей плана и в определенные в п. 1 моменты времени. Следует учитывать, что дублирование опытов невозможно. 4. Вычисление коэффициентов (производится аналогично расчетам в разд. 6.2 и 6.3). 5. Проверка адекватности модели. Пример 6.4. Пусть y – производительность труда работника. В начале рабочего дня она высокая. Варьируя моментами времени, можно устранить влияние временного фактора. Для этого необходимо ввести постоянную величину на характеристики временной зависимости t и определить момент времени, в который будет проводиться очередной опыт. Это позволяет получить оценки коэффициентов регрессии независимо от влияния временного фактора. Обработка эксперимента аналогична примеру 6.2. 📽️ ВидеоПолный факторный экспериментСкачать  ММХ. Модуль 8. Основы планирования многофакторного экспериментаСкачать 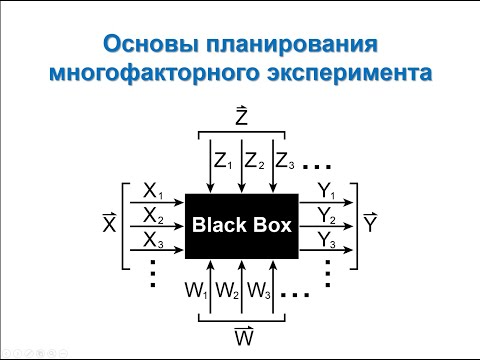 Математика #1 | Корреляция и регрессияСкачать  Метод наименьших квадратов. Регрессионный анализ.Скачать  Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать  Дробный факторный экспериментСкачать  Множественная регрессия в ExcelСкачать  Анализ производительности ПО при помощи математического планирования экспериментаСкачать  РЕГРЕССИОННЫЙ АНАЛИЗ STATISTICA #12Скачать  Множественная степенная регрессияСкачать  Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать  Лекция 7 Свойство полного и дробного МЕТСкачать  Эконометрика. Линейная парная регрессияСкачать  Регрессия в ExcelСкачать  design of experiments (DOE) примерСкачать  Центральные композиционные планыСкачать  Планированный трехфакторный экспериментСкачать  Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать  |
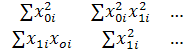
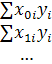
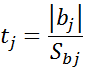










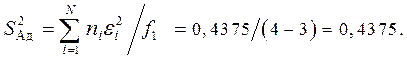





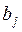









 . В один из блоков отберем опыты, для которых
. В один из блоков отберем опыты, для которых  = + 1, а в другой – опыты с
= + 1, а в другой – опыты с  .
.
 ;
;  ;
;

