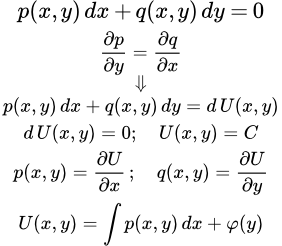Полный дифференциал функции заданная уравнением

Видео:Математический анализ, 30 урок, Полный дифференциалСкачать

Введение

Если найдена такая функция U ( x, y ) , то уравнение принимает вид:
dU ( x, y ) = 0 .
Его общий интеграл:
U ( x, y ) = C ,
где C – постоянная.

Если дифференциальное уравнение первого порядка записано через производную:
,
то его легко привести к форме (1). Для этого умножим уравнение на dx . Тогда . В результате получаем уравнение, выраженное через дифференциалы:
(1) .

Видео:11. Уравнения в полных дифференциалахСкачать

Свойство дифференциального уравнения в полных дифференциалах

Для того, чтобы уравнение (1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось соотношение:
(2) .

Доказательство

Далее мы полагаем, что все функции, используемые в доказательстве, определены и имеют соответствующие производные в некоторой области значений переменных x и y . Точка x ₀ , y ₀ также принадлежит этой области.

Докажем необходимость условия (2).
Пусть левая часть уравнения (1) является дифференциалом некоторой функции U ( x, y ) :
.
Тогда
;
.
Поскольку вторая производная не зависит от порядка дифференцирования, то
;
.
Отсюда следует, что . Необходимость условия (2) доказана.

Докажем достаточность условия (2).
Пусть выполняется условие (2):
(2) .
Покажем, что можно найти такую функцию U ( x, y ) , что ее дифференциал:
.
Это означает, что существует такая функция U ( x, y ) , которая удовлетворяет уравнениям:
(3) ;
(4) .
Найдем такую функцию. Проинтегрируем уравнение (3) по x от x ₀ до x , считая что y – это постоянная:
;
;
(5) .
Дифференцируем по y считая, что x – это постоянная и применим (2):

.
Уравнение (4) будет выполнено, если
.
Интегрируем по y от y ₀ до y :
;
;
.
Подставляем в (5):
(6) .
Итак, мы нашли функцию, дифференциал которой
.
Достаточность доказана.

В формуле (6), U ( x ₀ , y ₀) является постоянной – значением функции U ( x, y ) в точке x ₀ , y ₀ . Ей можно присвоить любое значение.

Видео:Полный дифференциалСкачать

Как распознать дифференциальное уравнение в полных дифференциалах

Рассмотрим дифференциальное уравнение:
(1) .
Чтобы определить, является ли это уравнение в полных дифференциалах, нужно проверить выполнение условия (2):
(2) .
Если оно выполняется, то это уравнение в полных дифференциалах. Если нет – то это не уравнение в полных дифференциалах.

Пример

Проверить, является ли уравнение в полных дифференциалах:
.

Здесь
, .
Дифференцируем по y , считая x постоянной:

.
Дифференцируем по x , считая y постоянной:

.
Поскольку:
,
то заданное уравнение – в полных дифференциалах.

Видео:Дифференциал функцииСкачать

Методы решения дифференциальных уравнений в полных дифференциалах

Метод последовательного выделения дифференциала

Наиболее простым методом решения уравнения в полных дифференциалах является метод последовательного выделения дифференциала. Для этого мы применяем формулы дифференцирования, записанные в дифференциальной форме:
du ± dv = d ( u ± v ) ;
v du + u dv = d ( uv ) ;
;
.
В этих формулах u и v – произвольные выражения, составленные из любых комбинаций переменных.

Пример 1

Ранее мы нашли, что это уравнение – в полных дифференциалах. Преобразуем его:
(П1) .
Решаем уравнение, последовательно выделяя дифференциал.
;
;
;
;

.
Подставляем в (П1):
;
.

Метод последовательного интегрирования

В этом методе мы ищем функцию U ( x, y ) , удовлетворяющую уравнениям:
(3) ;
(4) .

Проинтегрируем уравнение (3) по x , считая y постоянной:
.
Здесь φ ( y ) – произвольная функция от y , которую нужно определить. Она является постоянной интегрирования. Подставляем в уравнение (4):
.
Отсюда:
.
Интегрируя, находим φ ( y ) и, тем самым, U ( x, y ) .

Пример 2

Решить уравнение в полных дифференциалах:
.

Ранее мы нашли, что это уравнение – в полных дифференциалах. Введем обозначения:
, .
Ищем Функцию U ( x, y ) , дифференциал которой является левой частью уравнения:
.
Тогда:
(3) ;
(4) .
Проинтегрируем уравнение (3) по x , считая y постоянной:
(П2)
.
Дифференцируем по y :

.
Подставим в (4):
;
.
Интегрируем:
.
Подставим в (П2):

.
Общий интеграл уравнения:
U ( x, y ) = const .
Объединяем две постоянные в одну.

Метод интегрирования вдоль кривой

Функцию U , определяемую соотношением:
dU = p ( x, y ) dx + q ( x, y ) dy ,
можно найти, если проинтегрировать это уравнение вдоль кривой, соединяющей точки ( x ₀ , y ₀) и ( x, y ) :
(7) .
Поскольку
(8) ,
то интеграл зависит только от координат начальной ( x ₀ , y ₀) и конечной ( x, y ) точек и не зависит от формы кривой. Из (7) и (8) находим:
(9) .
Здесь x ₀ и y ₀ – постоянные. Поэтому U ( x ₀ , y ₀) – также постоянная.

Пример такого определения U был получен при доказательстве свойства уравнения в полных дифференциалах:
(6) .
Здесь интегрирование производится сначала по отрезку, параллельному оси y , от точки ( x ₀ , y ₀ ) до точки ( x ₀ , y ) . Затем интегрирование производится по отрезку, параллельному оси x , от точки ( x ₀ , y ) до точки ( x, y ) .

В более общем случае, нужно представить уравнение кривой, соединяющей точки ( x ₀ , y ₀ ) и ( x, y ) в параметрическом виде:
x ₁ = s ( t ₁) ; y ₁ = r ( t ₁) ;
x ₀ = s ( t ₀) ; y ₀ = r ( t ₀) ;
x = s ( t ) ; y = r ( t ) ;
и интегрировать по t ₁ от t ₀ до t .

Наиболее просто выполняется интегрирование по отрезку, соединяющим точки ( x ₀ , y ₀ ) и ( x, y ) . В этом случае:
x ₁ = x ₀ + ( x – x ₀) t ₁ ; y ₁ = y ₀ + ( y – y ₀) t ₁ ;
t ₀ = 0 ; t = 1 ;
dx ₁ = ( x – x ₀) dt ₁ ; dy ₁ = ( y – y ₀) dt ₁ .
После подстановки, получается интеграл по t от 0 до 1 .
Данный способ, однако, приводит к довольно громоздким вычислениям.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Автор: Олег Одинцов . Опубликовано: 10-08-2012 Изменено: 02-07-2015

Видео:14. Что такое параметрически заданная функция, производная параметрически заданной функции.Скачать

Уравнения в полных дифференциалах

В этой теме мы рассмотрим метод восстановления функции по ее полному дифференциалу, дадим примеры задач с полным разбором решения.

Бывает так, что дифференциальные уравнения (ДУ) вида P ( x , y ) d x + Q ( x , y ) d y = 0 могут содержать в левых частях полные дифференциалы некоторых функций. Тогда мы можем найти общий интеграл ДУ, если предварительно восстановим функцию по ее полному дифференциалу.

Рассмотрим уравнение P ( x , y ) d x + Q ( x , y ) d y = 0 . В записи левой его части содержится дифференциал некоторой функции U ( x , y ) = 0 . Для этого должно выполняться условие ∂ P ∂ y ≡ ∂ Q ∂ x .

Полный дифференциал функции U ( x , y ) = 0 имеет вид d U = ∂ U ∂ x d x + ∂ U ∂ y d y . С учетом условия ∂ P ∂ y ≡ ∂ Q ∂ x получаем:

P ( x , y ) d x + Q ( x , y ) d y = ∂ U ∂ x d x + ∂ U ∂ y d y

∂ U ∂ x = P ( x , y ) ∂ U ∂ y = Q ( x , y )

Преобразовав первое уравнение из полученной системы уравнений, мы можем получить:

U ( x , y ) = ∫ P ( x , y ) d x + φ ( y )

Функцию φ ( y ) мы можем найти из второго уравнения полученной ранее системы:
∂ U ( x , y ) ∂ y = ∂ ∫ P ( x , y ) d x ∂ y + φ y ‘ ( y ) = Q ( x , y ) ⇒ φ ( y ) = ∫ Q ( x , y ) — ∂ ∫ P ( x , y ) d x ∂ y d y

Так мы нашли искомую функцию U ( x , y ) = 0 .

Найдите для ДУ ( x 2 — y 2 ) d x — 2 x y d y = 0 общее решение.

P ( x , y ) = x 2 — y 2 , Q ( x , y ) = — 2 x y

Проверим, выполняется ли условие ∂ P ∂ y ≡ ∂ Q ∂ x :

∂ P ∂ y = ∂ ( x 2 — y 2 ) ∂ y = — 2 y ∂ Q ∂ x = ∂ ( — 2 x y ) ∂ x = — 2 y

Наше условие выполняется.

На основе вычислений мы можем сделать вывод, что левая часть исходного ДУ является полным дифференциалом некоторой функции U ( x , y ) = 0 . Нам нужно найти эту функцию.

Так как ( x 2 — y 2 ) d x — 2 x y d y является полным дифференциалом функции U ( x , y ) = 0 , то

∂ U ∂ x = x 2 — y 2 ∂ U ∂ y = — 2 x y

Интегрируем по x первое уравнение системы:

U ( x , y ) = ∫ ( x 2 — y 2 ) d x + φ ( y ) = x 3 3 — x y 2 + φ ( y )

Теперь дифференцируем по y полученный результат:

∂ U ∂ y = ∂ x 3 3 — x y 2 + φ ( y ) ∂ y = — 2 x y + φ y ‘ ( y )

Преобразовав второе уравнение системы, получаем: ∂ U ∂ y = — 2 x y . Это значит, что
— 2 x y + φ y ‘ ( y ) = — 2 x y φ y ‘ ( y ) = 0 ⇒ φ ( y ) = ∫ 0 d x = C

где С – произвольная постоянная.

Получаем: U ( x , y ) = x 3 3 — x y 2 + φ ( y ) = x 3 3 — x y 2 + C . Общим интегралом исходного уравнения является x 3 3 — x y 2 + C = 0 .

Разберем еще один метод нахождения функции по известному полному дифференциалу. Он предполагает применение криволинейного интеграла от фиксированной точки ( x 0 , y 0 ) до точки с переменными координатами ( x , y ) :

U ( x , y ) = ∫ ( x 0 , y 0 ) ( x , y ) P ( x , y ) d x + Q ( x , y ) d y + C

В таких случаях значение интеграла никак не зависит от пути интегрирования. Мы можем взять в качестве пути интегрировании ломаную, звенья которой располагаются параллельно осям координат.

Найдите общее решение дифференциального уравнения ( y — y 2 ) d x + ( x — 2 x y ) d y = 0 .

Проведем проверку, выполняется ли условие ∂ P ∂ y ≡ ∂ Q ∂ x :

∂ P ∂ y = ∂ ( y — y 2 ) ∂ y = 1 — 2 y ∂ Q ∂ x = ∂ ( x — 2 x y ) ∂ x = 1 — 2 y

Получается, что левая часть дифференциального уравнения представлена полным дифференциалом некоторой функции U ( x , y ) = 0 . Для того, чтобы найти эту функцию, необходимо вычислить криволинейный интеграл от точки ( 1 ; 1 ) до ( x , y ) . Возьмем в качестве пути интегрирования ломаную, участки которой пройдут по прямой y = 1 от точки ( 1 , 1 ) до ( x , 1 ) , а затем от точки ( x , 1 ) до ( x , y ) :

∫ ( 1 , 1 ) ( x , y ) y — y 2 d x + ( x — 2 x y ) d y = = ∫ ( 1 , 1 ) ( x , 1 ) ( y — y 2 ) d x + ( x — 2 x y ) d y + + ∫ ( x , 1 ) ( x , y ) ( y — y 2 ) d x + ( x — 2 x y ) d y = = ∫ 1 x ( 1 — 1 2 ) d x + ∫ 1 y ( x — 2 x y ) d y = ( x y — x y 2 ) y 1 = = x y — x y 2 — ( x · 1 — x · 1 2 ) = x y — x y 2

Мы получили общее решение дифференциального уравнения вида x y — x y 2 + C = 0 .

Определите общее решение дифференциального уравнения y · cos x d x + sin 2 x d y = 0 .

Проверим, выполняется ли условие ∂ P ∂ y ≡ ∂ Q ∂ x .

Так как ∂ ( y · cos x ) ∂ y = cos x , ∂ ( sin 2 x ) ∂ x = 2 sin x · cos x , то условие выполняться не будет. Это значит, что левая часть дифференциального уравнения не является полным дифференциалом функции. Это дифференциальное уравнение с разделяющимися переменными и для его решения подходят другие способы решения.

Видео:10. Полное приращение и полный дифференциал функции двух переменныхСкачать

Дифференциал функции онлайн

Дифференциалом функции называется главная (линейная по ) часть приращения функции. Чтобы понять данное определение, рассмотрим следующий рисунок.

На рисунке изображён график функции и касательной к ней в точке . Дадим аргументу функции некоторое приращение , тогда функция также получит некоторое приращение . Величина называется дифференциалом функции . При этом, из графика следует, что равно приращению ординаты касательной, проведённой в точке к функции . Именно поэтому дифференциалом называют линейную часть приращения функции, т.е. приращение ординаты касательной.

Из рисунка следует, что угол наклона касательной , который она образует с положительным направлением оси и — равны. Кроме того, тангенс угла наклона касательной равен значению производной функции в точке касания:

Из треугольника следует, что:

Таким образом, дифференциал функции выражается следующей формулой:

Рассмотрим ещё такой момент: из рисунка следует, что , причем . Причем, чем меньше , тем меньший вклад в величину вносит значение . Т.е. при достаточно малых значениях , можно считать, что . Данное соотношение позволяет вычислять приближенное значение функции в точке , если известно её значение в точке .

Дифференциал высшего порядка (например порядка ) определяется как дифференциал от дифференциала -ого порядка:

Например, дифференциал второго порядка вычисляется следующим образом:

Аналогичным образом получаем формулу для вычисления дифференциала -ого порядка:

где — -ая производная функции по переменной .

Пару слов стоит сказать о вычислении дифференциала функции многих переменных, который в этом случае называется полным дифференциалом. Полный дифференциал функции, зависящей от -переменных определяется по формуле:

Выражения для дифференциалов высших порядков функции многих переменных можно получить исходя из общей формулы:

В общем случае, для возведения суммы в -ую степень необходимо воспользоваться формулой бинома Ньютона. Рассмотрим процесс получения формулы полного дифференциала второго порядка функции двух переменных:

Наш онлайн калькулятор способен вычислить дифференциалы разных порядков для любых функций одной или нескольких переменных с описанием подробного решения на русском языке.

📽️ Видео

11. Производная неявной функции примерыСкачать

27. Дифференцирование неявной функции двух переменныхСкачать

25. Как найти дифференциал второго порядка функции двух переменных (часть 2)Скачать

11. Полный дифференциал примеры решения (часть 1)Скачать

29. Частные производные и дифференциал функции заданной неявно. примерСкачать

18+ Математика без Ху!ни. Производная неявной функции.Скачать

21. Дифференциал функцииСкачать

Математика без Ху!ни. Частные производные функции нескольких переменных. Градиент.Скачать

Математика Без Ху!ни. Производная функции, заданной параметрически.Скачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

24. Вычисление дифференциала. Дифференциал неявной функцииСкачать

Дифференциал: частный и полный дифференциалСкачать

Частные производные функции многих переменныхСкачать

17. Полный дифференциал сложной функции. Инвариантность формы первого дифференциалаСкачать