- План лекции:
- ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПАРАМЕТРЫ ПОВЕРХНОСТНОГО СЛОЯ
- ГЕОМЕТРИЧЕСКИЕ ПАРАМЕТРЫ ПОВЕРХНОСТИ
- ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ( ).
- Физический смысл
- КОГЕЗИОННЫЕ И ПОВЕРХНОСТНЫЕ СИЛЫ
- ВНУТРЕННЯЯ (ПОЛНАЯ) УДЕЛЬНАЯ ПОВЕРХНОСТНАЯ ЭНЕРГИЯ. ЗАВИСИМОСТЬ ЭНЕРГЕТИЧЕСКИХ ПАРАМЕТРОВ ПОВЕРХНОСТИ ОТ ТЕМПЕРАТУРЫ.
- Природа поверхностной энергии. Поверхностное натяжение
- Термодинамика поверхностного слоя
- 🎥 Видео
План лекции:
Видео:Свободная энергия Гиббса. 10 класс.Скачать

ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПАРАМЕТРЫ ПОВЕРХНОСТНОГО СЛОЯ
ГЕОМЕТРИЧЕСКИЕ ПАРАМЕТРЫ ПОВЕРХНОСТИ
Межфазные поверхности могут существовать только при наличии в системе жидкой или твердой фазы. Межфазную поверхность т-ж определяет профиль поверхности твердого тела. Поверхностный слой на межфазных границах имеет одну часть в первой фазе, другую – во второй.
Удельная поверхность тела определяется отношением площади его поверхности S 1,2 между фазами 1 и 2 к объему тела V .

Поверхность между фазами может быть отнесена к дисперсной фазе или к дисперсной среде. Обычно при определении удельной поверхности дисперсной системы ее относят к объему дисперсной фазы.
Дисперсные системы с одинаковыми по размерам частицами дисперсной фазы называются монодисперсными, с разными – полидисперсными.
Если поверхность и объем дисперсной фазы междисперсной системы выразить через поверхность и объем отдельных частиц, то число частиц будет входить и в числитель и в знаменатель. Поэтому S уд монодисперсной системы можно определить, зная размер отдельных частиц. Например, для частиц кубических с размерами ребра 1 и сферическим диаметром d :

для сферических частиц:

k – коэффициент формы частиц.
Часто S уд относят к массе дисперсной фазы:


Изменение S уд с изменением дисперсности зависит от формы частиц.
SHAPE * MERGEFORMAT



Зависимость возрастает, т. к. возрастает коэффициент формы.
Более конкретная характеристика дисперсности кривизна поверхности, определяемая производной площади поверхности по объему.
Видео:Свободная энергия Гиббса и самопроизвольные реакции (видео 8) | Энергия| БиологияСкачать

ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ (  ).
).


Термодинамическое определение 
dU = TdS – pdV + 


При S, V, n, q — const:



т.е. 

т.е. в общем виде, 

единицы измерения: СИ Дж/м 2 = Н*м/м 2 = Н/м
СГС Эр1/см 2 , Дин/см.
Физический смысл 
1. Работа, расходуемая на разрыв межмолекулярной связи. Чем сильней межмокулярные связи в данном теле, тем больше его 
2. Сила, направленная параллельно к поверхности. Поверхностные молекулы, обладая избыточной энергией, стремятся уйти вглубь конденсированной фазы и сжимают поверхность.
Видео:Лекция 13. Энергия Гиббса и ГельмгольцаСкачать

КОГЕЗИОННЫЕ И ПОВЕРХНОСТНЫЕ СИЛЫ
Когезия — взаимодействие молекул, атомов, ионов внутри одной фазы.
W к = 2 
т.к. определяется затратой энергии на обратимый разрыв тела по сечению равному единице площади.
Точную информацию о когезии и поверхностном натяжении можно получить из т/д характеристик тел, связанных с парообразованием.
В процессе испарения происходит полный разрыв межмолекулярных связей, поэтому работа когезии определяется энтальпией парообразования.



При равновесии при р, Т = const 


Отсюда следует, что, чем больше энтальпия парообразования (т.е. больше работа когезии, а значит и поверхностное натяжение), тем меньше давление насыщенного пара над веществом, т.к.


где 
При кипении р/ратм = 1
L = Ткип 

L — энтальпия парообразования при Ткип.
Свойства поверхности отражают природу ионов, атомов и молекул в ней.
Для жидкостей и твердых тел когезионные силы выражаются в межмолекулярном взаимодействии, обусловленном ван-дер-ваальсовыми и водородными связями. Оно отличается от химического взаимодействия отсутствующей специфичностью и насыщаемостью небольшими энергиями. Разрыв таких связей приводит к формированию поверхностей, способных образовывать ван-дер-ваальсовые и водородные связи с молекулами, попадающими на эту поверхность.
Видео:2 4 Свободная энергия ГиббсаСкачать

ВНУТРЕННЯЯ (ПОЛНАЯ) УДЕЛЬНАЯ ПОВЕРХНОСТНАЯ ЭНЕРГИЯ. ЗАВИСИМОСТЬ ЭНЕРГЕТИЧЕСКИХ ПАРАМЕТРОВ ПОВЕРХНОСТИ ОТ ТЕМПЕРАТУРЫ.
За толщину поверхностного слоя принимают расстояние по обе стороны от границы раздела фаз, за пределами которой свойства слоя перестают отличаться от свойств объемных фаз.
Установление границ поверхностного слоя со стороны объемных фаз трудная задача. Гиббс предложил относить все изменения т/д параметров в слое к разделяющей поверхности, не имеющей объема или толщины (метод избыточных величин Гиббса).
G = G 1 + G 2 + 
G – энергия Гиббса системы;
G 1 и G 2 – энергия Гиббса объемных фаз;

Избыточная внутренняя энергия:
Индекс « s » указывает на то, что потенциалы отнесены к единице поверхности.
q s = TS s теплота образования единицы поверхности (скрытая теплота образования, она равна количеству теплоты, которую нужно сообщить телу, чтобы при постоянной температуре увеличить его поверхность на единицу площади).
Учитывая, что G s = 
U s = 
Из уравнения 2.15 следует, что внутренняя энергия поверхности складывается из энергии Гиббса и теплоты образования поверхности.
Из объединенного уравнения, при постоянстве всех параметров, кроме температуры, имеем:
dGs = — S dT или ( 

Подставляя (2.16) в (2.14) или (2.15), получаем:
U s = 



(2.17) – уравнение Гиббса-Гельмгольца, оно связывает поверхностную энергию с поверхностным напряжением, следовательно, для определения полной поверхностной энергии нужно знать зависимость поверхностного напряжения от температуры. Конкретную зависимость можно получить только экспериментально, но качественные выводы можно сделать из уравнения (2.17).
qS – всегда больше 0. (для индивидуального вещества).
( 








Для большинства жидкостей поверхностная энергия почти не зависит от температуры.
Чтобы убедиться в этом проинтегрируем по температуре (2.17)
( 










( 






( 

Видео:Свободная энергия Гиббса и спонтанностьСкачать
Природа поверхностной энергии. Поверхностное натяжение
» data-shape=»round» data-use-links data-color-scheme=»normal» data-direction=»horizontal» data-services=»messenger,vkontakte,facebook,odnoklassniki,telegram,twitter,viber,whatsapp,moimir,lj,blogger»>
Природа поверхностной энергии. Поверхностное натяжение. ТЕРМОДИНАМИКА МЕЖФАЗНОЙ ПОВЕРХНОСТНОСТИ
Наиболее важной характеристикой поверхности является поверхностное натяжение а.
Поверхностное натяжение – это избыточная энергия, приходящаяся на единицу площади поверхности:
Физическая природа поверхностного натяжения в нескомпенсированности поля межмолекулярных сил на межфазных поверхностях.
Поверхностное натяжение характеризует различия в интенсивности межмолекулярных взаимодействий граничащих фаз. Чем сильнее межмолекулярные связи в веществе, тем больше поверхностное натяжение на его межфазной поверхности.
С термодинамической точки зрения, поверхностное натяжение определяется частной производной от любого термодинамического потенциала по величине площади межфазной поверхности при постоянстве других параметров. Используя потенциал Гиббса (G), можно записать
где р – давление; Т- температура; п. – число молей компонентов.
Поверхностная энергия является частью свободной энергии системы в целом. В самопроизвольных процессах эта энергия может быть снижена либо за счет уменьшения площади поверхности и изменения ее формы, либо за счет снижения поверхностного натяжения.
Факторы, влияющие на поверхностное натяжение
Поверхностное натяжение на границе раздела фаз между жидкостью и газом определяют следующие факторы: химическая природа вещества, температура, природа граничащих фаз, наличие примесей, заряд поверхности, кривизна поверхности жидкости.
Энергия межмолекулярных взаимодействий зависит от температуры, а значит, имеет выраженную температурную зависимость.
Взаимосвязь поверхностного натяжения, температуры и полной поверхностной энергии (внутренней энергии поверхностного слоя) Us выражается уравнением Гиббса – Гельмгольца:
Для многих веществ температурные коэффициенты поверхностного натяжения находятся в диапазоне от -0,1 до 0,2 мДж/(м 2 *К).
Рис. 2.1. Зависимость поверхностного натяжения жидкостей от температуры: вода (У), глицерин (2), нитробензол (3), гексан (4).
С повышением температуры поверхностное натяжение уменьшается, а теплота образования единицы площади поверхности увеличивается. Это объясняется тем, что с повышением температуры расстояние между молекулами в жидких телах увеличивается, и соответственно равнодействующая межмолекулярных сил (и, следовательно, поверхностное натяжение) уменьшается. С помощью температурного коэффициента можно определить поверхностное натяжение при любой температуре, если известно значение поверхностного натяжения при какой-то температуре, т. е.
Появление кривизны поверхности из-за стремления системы
к минимуму поверхностной энергии ведет не только к изменению площади межфазной поверхности, но и к появлению избыточного давления внутри фаз. Взаимосвязь между избыточным внутренним давлением в теле и кривизной его поверхности выражается уравнением Лапласа:
Искривление поверхности вызывает повышение или понижение давления в фазе по сравнению с плоской поверхностью фазы такого же химического состава. Очевидно, что это приводит к изменению термодинамических параметров вещества, которые определяют его физические свойства и реакционную способность. Понятие термодинамическая реакционная способность вещества характеризует его способность изменять химический или фазо
вый состав, т. е. вступать в химическую реакцию или переходить в новую фазу (например, испаряться или конденсироваться, растворяться).
У тел с искривленной поверхностью меняется не только внутреннее давление, но и его свободная энергия
Уравнение показывает, что приращение реакционной способности пропорционально 1/r- кривизне поверхности или дисперсности. Чем выше кривизна поверхности или дисперсность, тем выше ее влияние на реакционную способность.
При переходе из газообразного состояния в жидкое
гдер – давление пара над искривленной поверхностью; ps– давление пара над плоской поверхностью.
Тогда уравнение, записанное для сферической поверхности, называется уравнением капиллярной конденсации Кельвина (Томсона):
Из анализа данного уравнения можно сделать вывод о том, что при положительной кривизне жидкости (капля в невесомости или на поверхности твердого тела при отсутствии или неполной смачиваемости) над ней создается повышенное по сравнению с плоской поверхностью давление пара, т. е. испаряется больше жидкости. При отрицательной кривизне (жидкость, смачивающая капилляр) количество испарившейся жидкости в равновесии с ее паром будет меньше по сравнению с плоской поверхностью; иными словами, конденсация будет происходить при меньшем давлении паров.
При появлении кривизны поверхности и увеличении степени дисперсности уменьшается и температура фазовых переходов.
Свободная энергия единицы поверхности и поверхностное натяжение
3.1. Поверхностные свойства веществ
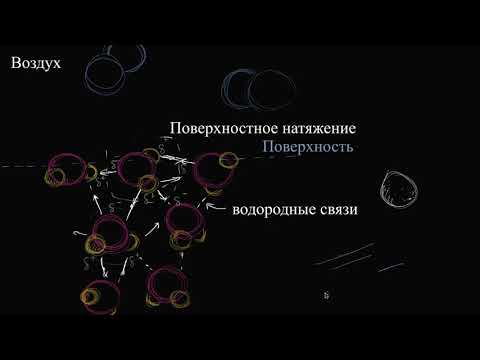
Если взять частицу внутри жидкости и, рассматривая ее как точку, провести сферу радиуса действия межчастичных сил, то за промежуток времени, больший по сравнению с периодом собственных колебаний, на частицу будут действовать силы, одинаковые во всех направлениях.
Следовательно, силовое поле атомов или молекул в объеме жидкости симметрично. Частицы в глубине и на поверхности имеют разные силовые поля. На поверхности жидкости частица будет испытывать преимущественное притяжение со стороны жидкой фазы. Если вторая фаза — пар или газ, то силами взаимодействия со стороны другой фазы можно пренебречь. Если вторая фаза — жидкость, то равнодействующая будет другая.
В общем случае межчастичные силы на межфазной границе несимметричны. Наличие такой асимметрии силового поля приводит к тому, что появляется равнодействующая, направленная перпендикулярно поверхности. Под действием этой силы поля частица втягивается вглубь жидкости. Если частицы уподобить шарикам, то перемещение подвижных частиц жидкости можно проиллюстрировать следующим рис. 3.3:
Когда частица из поверхностного слоя уйдет в объем жидкости, между оставшимися двумя соседними частицами будут действовать силы притяжения. Силы притяжения между частицами В и С сближают поверхностные частицы, поэтому жидкость самопроизвольно сокращает свою поверхность. Такой характер поведения жидкости обусловлен ее текучестью. Если на жидкость не действуют никакие другие силы, то жидкость принимает форму сферы, обладающей минимальной поверхностью. Если же действуют силы тяжести, то форма жидкости может быть другой. При малом объеме жидкости поверхностные силы намного превосходят силы тяжести и жидкость собирается в сферическую капельку. По мере увеличения объема жидкости эти силы становятся соизмеримыми и получается приплюснутая капля. В случае большого объема жидкости силы тяжести значительно больше поверхностных сил и жидкость принимает форму сосуда.
Если увеличивать поверхность жидкости, то на это увеличение нужно затрачивать работу: δА — работа увеличения поверхности на dω. При обратимом изотермическом процессе эта работа максимальна и равна убыли свободной энергии системы: δАмакс = –dF. Изменение свободной энергии, отнесенной к единице поверхности при постоянных объеме и температуре (V, T = const), называется свободной энергией единицы поверхности, или поверхностным натяжением.
F Работа δА отрицательна, так как работу совершаем мы, а не система. Размерность поверхностного натяжения:
Энергия на единицу поверхности. Эти размерности можно преобразовать:
Сила, действующая на поверхности жидкости, направленная по касательной к этой поверхности. Эту силу называют поверхностным натяжением — это сила на единицу длины, действующая по касательной к поверхности. Количественно свободная энергия единицы поверхности жидкости равна поверхностному натяжению, однако отождествлять их нельзя. Энергия — это скалярная величина, а сила — векторная. Они совпадают только в изотропных средах. В анизотропных средах (кристаллах) эти характеристики могут существенно отличаться. В кристаллических телах сила — не вектор, а тензор. Вектор можно задать тремя числами, а тензор определяется числовой матрицей, т. е. набором чисел. Если этих чисел три, то имеем вектор r (x, y, z). Если состояние напряженное, то надо знать напряжение по различным направлениям.
Натяжение в общем случае нужно рассматривать как тензор. Поэтому в кристаллах нельзя отождествлять свободную энергию и поверхностное натяжение. В жидкости они совпадают количественно, и обычно в литературе их отождествляют:
Поверхностное натяжение жидкостей обычно определяют на границе с их собственным насыщенным паром или инертным газом. Величина свободной энергии зависит от свойств жидкости и является вполне определенной. Поверхностное натяжение жидкости — ее свойство, ее характеристика при данной температуре. Натяжение на границе двух конденсированных фаз (ж1‑ж2, ж‑тв) зависит от свойств каждой жидкости и является их совместной характеристикой. Поэтому его называют межфазным натяжением. Размерность та же.
Для конденсированных фаз при малых давлениях F ≈ G, и обычно технологи пользуются энергией Гиббса. F (V, T), G (P, T) — в скобках записаны независимые переменные.
Правильнее было бы обозначать как σ V и σ Р . σ V — работа образования единицы поверхности при неизменном объеме системы; σ Р — работа образования единицы поверхности при постоянном давлении. Если изменение объема ΔV мало, что характерно для конденсированных фаз, то этими различиями можно пренебречь.
Для чистых жидкостей при малых давлениях PdV → 0 . Если давление большое, то σР > σV на работу против сил внешнего давления. Для чистых жидкостей это справедливо, а для растворов эти понятия не тождественны (т. к. имеем различные структурные коэффициенты). В дальнейшем мы будем рассматривать небольшие давления и считать, что σР = σV
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 2.1.
При конденсации тумана, состоящего из капель кадмия, образовалось 12,5 • 10 -6 м 3 жидкого кадмия. Поверхностное натяжение при температуре конденсации равно 570 мДж/м 2 . Свободная поверхностная энергия всех капель составляла 53 Дж. Вычислите дисперсность и диаметр капель жидкого кадмия.
Пример 2.2.
Рассчитать давление насыщенных паров над каплями воды с дисперсностью 0,1 нм -1 при 293 К. Давление над плоской поверхностью при этой температуре составляет 2338 Па, р = 1 г/см 3 , поверхностное натяжение 72,7 мДж/м 2 , мольный объем 18 • 10 -6 м 3 /моль.
Пример 2.3.
В воздухе, содержащем пары воды, образуется туман при температуре 270 К. Степень пересыщения составляет 3,01. Поверхностное натяжение 73 мДж/м 2 , мольный объем вещества в конденсированном состоянии 18*10 -6 м 3 /моль. Рассчитать критический размер ядер конденсации и число молекул, содержащихся в них.
Пример 2.4.
По экспериментальным данным (табл. 2.1) температурной зависимости поверхностного натяжения найти температурный коэффициент.
Видео:Вывод формул для энергии Гельмгольца, Гиббса и энтальпии с помощью преобразования ЛежандраСкачать

Термодинамика поверхностного слоя
Термодинамическая характеристика дисперсных систем. Термодинамический метод избыточных величин Гиббса и метод «слоя конечной толщины.
Дисперсной называют систему, в которой одно вещество распределено в среде другого, причем между частицами и дисперсионной средой есть граница раздела фаз. Дисперсные системы состоят из дисперсной фазы и дисперсионной среды.
Дисперсная фаза — это частицы, распределенные в среде. Ее признаки: дисперсность и прерывистость (рис. 1.1.1.1).
Дисперсионная среда — материальная среда, в которой находится дисперсная фаза. Ее признак — непрерывность .
Поверхность раздела фаз характеризуется раздробленностью и гетерогенностью. Раздробленность характеризуется:
1) степенью дисперсности : 
2) дисперсностью — величиной, обратной минимальному размеру:



3)удельной поверхностью : 

4) кривизной поверхности : 

где r 1 и r 2 — радиусы окружностей при прохождении через поверхность и нормаль к ней в данной точке двух перпендикулярных плоскостей.
5) размером тела по трем осям , причем определяющим является размер по той оси, где он минимальный. В зависимости от размеров частиц они имеют свои исторические названия (см. рис. 1.1.1.1).
Лиофильные системы – в них дисперсная фаза взаимодействует с дисперсионной средой и при определенных условиях способна в ней растворяться – растворы коллоидных ПАВ, растворы ВМС. Свободная энергия системы DF 0;
где W ког — работа когезии;
W сольв — работа сольватации.
При DU > 0, DU DU . Эта группа характеризуется малым значением поверхностного натяжения на границе раздела фаз.
Лиофобные системы – в них дисперсная фаза не способна взаимодействовать с дисперсионной средой и растворяться в ней. Для них DF > 0. Диспергирование в этом случае совершается либо за счет внешней работы, либо за счет других процессов, идущих в системе спонтанно (химическая реакция) и характеризуется высоким значением поверхностного натяжения на границе раздела фаз, что соответствует малому значению энергии сольватации.
Существует две группы способов получения дисперсных систем:
1. Способы диспергирования заключаются в раздроблении тела до коллоидного состояния (мукомольное производство).
2. Способы конденсации заключаются в укрупнении частиц, атомов, молекул до частиц коллоидных размеров (химическая реакция с образованием осадка).
Как уже отмечалось, на границе раздела фаз существует избыток свободной энергии. Процесс увеличения площади поверхности при постоянном объеме выводит молекулы из глубины фазы на поверхностный слой, совершая при этом работу против межмолекулярных сил. Эта работа в изотермических условиях равна увеличению свободной поверхностной энергии. Для описания термодинамики поверхностных явлений используют два метода:
1. Метод избыточных величин Гиббса .
2. Метод слоя конечной толщины .
За толщину поверхностного слоя принимаем расстояние по обе стороны границы раздела фаз, за пределами которого свойства слоя перестают отличаться от свойств фазы в объеме.
Определение границы поверхностного слоя задача очень сложная, поэтому Гиббсом предложено относить все изменения термодинамических параметров слоя разделяющей поверхности, не имеющей объема и толщины. При таком рассмотрении поверхность будет обладать избыточными термодинамическими параметрами, непосредственно отражающими проявление поверхностной энергии. В соответствии метода Гиббса позиция 1 на рис. 2.1.1.1 – энергия системы равна сумме энергий Гиббса объемных фаз DG 1 и 

В методе слоя конечной толщины рассматривается поверхностный слой, имеющий определенные размеры (позиция II на рис. 2.1.1.1). Его термодинамические параметры включают как поверхностную энергию, так и энергию объема слоя, имеющего те же свойства, что и объемная фаза. Этот метод не рассматриваем. В методе Гиббса все экстенсивные величины выражаются в виде избытков по сравнению со значением этих величин в реальных объемных фазах.
Тема 2.1.2. Поверхностное натяжение. Методы измерения поверхностного натяжения. Зависимость поверхностного натяжения от температуры и концентрации. Уравнение Шишковского
На образование коллоидной системы затрачивается работа А= × S , где коэффициент пропорциональности; S — новая поверхность.
Поверхностное натяжение есть частная производная от любого термодинамического потенциала по площади межфазной поверхности при постоянстве соответствующих параметров.
Если проводить процесс образования новой поверхности изотермически и обратимо, то вся работа перейдет в запас свободной энергии поверхности: A = F s , F s = s×S ; 
Коэффициент s — поверхностное натяжение; — это работа, совершаемая для образования единицы новой поверхности.
Поверхностное натяжение — это сила, действующая на единицу длины контура, ограниченного единицей поверхности и направленная в сторону сокращения поверхности, перпендикулярно к контуру вовнутрь его.
Наиболее часто используются 4 метода определения поверхностного натяжения.
1. Метод максимального давления в пузырьке газа (метод Ребиндера) (рис. 2.1.2.1, а).
Основан на продавливании пузырька газа (воздуха) под воздействием внешнего давления р через калиброванный капилляр радиусом r 0 . С увеличением давления пузырек растет, а радиус кривизны его поверхности R превышает радиус капилляра (положение 1 рис. 2.1.2.1, а : R > r 0 ). Дальнейшее увеличение объема пузырька будет происходить до тех пор, пока внутреннее давление достигнет своего максимального значения; радиус кривизны при этом будет минимальным, т.е. R = r 0 (положение 2). В этот момент пузырек теряет устойчивость: при увеличении его объема он отрывается от капилляра. Если в момент отрыва пузырька измерить давление р , то поверхностное натяжение можно представить


Чтобы не измерять радиус капилляра, можно определить р для жидкости, поверхностное натяжение которой известно (эталон, часто, вода). Отсюда

Исключив в уравнениях (1) и (2) радиус капилляра, получим выражение для определения поверхностного натяжения

где 



2. Сталагмометрический метод (рис. 2.1.2.1, б).
Определяют вес капли, которая отрывается от капилляра под действием силы тяжести. Считают, что при отрыве вес капли Р к уравновешивается силой, равной произведению поверхностного натяжения и длины окружности капилляра радиусом r 0 :

где k – поправочный коэффициент, учитывающий, что отрыв капель происходит по радиусу шейки капли, который меньше радиуса самой капли.
Определяют экспериментально вес капель и при помощи разработанных таблиц с учетом (3) находят s. Рекомендуется увеличивать время формирования капли до тех пор, пока число капель станет постоянным.

где r — плотность исследуемой жидкости;
n – число капель исследуемой жидкости;
sст , rст , n ст – значения s, r и n для стандартной жидкости.
3. Метод отрыва кольца (рис. 2.1.2.1, в).
Измеряют силу F , которой противодействует поверхностное натяжение жидкости, смачивающей периметр поверхности кольца.

где k – поправочный коэффициент, учитывает, что поднимающийся при отрыве кольца столб жидкости не имеет формы правильного полого цилиндра.
Метод капиллярного поднятия (рис. 2.1.2.1, г).
В капилляре за счет смачивания образуется вогнутый мениск с радиусом кривизны r , поверхностное натяжениеsжг вызывает капиллярное давление Dр . Оно уравновешивается весом Р н столба жидкости высотой Н :

где q — краевой угол смачивания.
Капиллярное давление уравновешивается весом столба РН жидкости высотой Н , т.е. Dр = РН . С учетом (4) и веса столба жидкости можно записать:

где r, r0 – плотность жидкости и газа (воздуха).
В связи с тем, что r >> r0 , плотностью газа можно пренебречь, тогда высота подъема жидкости в капилляре определяется по формуле

Р и с. 2.1.2.1. Методы определения поверхностного натяжения: а — наибольшего давления в пузырьке, б – сталагмометрическим, в – отрыва кольца,
г – капиллярного поднятия
При полном смачивании, когда q = 0 и cosq = 1, имеем


гдеD r – разность плотностей жидкости и газовой фазы;
g – ускорение свободного падения;
а – капиллярная постоянная.
Поверхностное натяжение индивидуальных веществ (жидкостей) монотонно убывает с возрастанием температуры.



где 

D Т — разность температур;
а — температурный коэффициент; 

Это объясняется тем, что вначале вся поверхность раздела жидкой фазы свободна от поверхностно-активных веществ (ПАВ) и небольшое его количество, присутствующее в растворе, почти целиком уходит на поверхность. Затем следует криволинейный участок, отвечающий средней концентрации. В этих условиях значительная часть поверхности занята молекулами поверхностно-активных веществ (ПАВ), что снижает скорость повышения концентрации на границе раздела. Большим концентрациям на изотерме отвечает почти горизонтальный участок (кривая 3), показывающий, что поверхностное натяжение мало зависит от концентрации. При этих условиях на границе «жидкость – воздух» образуется сплошной монослой поверхностно-активного вещества (ПАВ), и увеличение его концентрации на границе невозможно в дальнейшем. При увеличении концентрации поверхностного инактивного вещества в растворе изотерма полого поднимается (кривая 2). Это объясняется тем, что поверхностные инактивные вещества благодаря высокому поверхностному натяжению и активности уходят в объем, а на границе раздела «жидкость – воздух» имеются лишь сравнительно небольшие концентрации вещества, попадающего туда за счет диффузии из объема раствора. При увеличении концентрации веществ, не влияющих на поверхностное натяжение, изотерма представляет собой прямую, параллельную оси концентрации. Следует отметить, что отнесение веществ к той или иной группе зависит от природы растворителя. Одно и тоже вещество для разных растворителей может быть и поверхностно-активным веществом (ПАВ), и не влиять на поверхностное натяжение.
Для малых и средних концентраций поверхностно-активных веществ (ПАВ) при описании зависимости 

где s 0 – поверхностное натяжение растворителя (Н/м);
c – концентрация поверхностно-активного вещества (ПАВ);
А, b – константы, данные в справочнике.
Уравнение Гиббса-Гельмгольца для поверхностной энергии. Полная поверхностная энергия
Запишем известное из термодинамики выражение внутренней энергии для поверхности.



В этом уравнении q s = T D S — теплота образования единицы поверхности в обратимом процессе. Она равна количеству теплоты, которую необходимо подвести к системе, чтобы увеличить ее поверхность на единицу при T = const . Из уравнений фазы при постоянстве всех параметров, кроме температуры, имеем:
dG s = — S s dT , 
Подставляя эти значения в уравнение полной поверхностной энергии, получаем:

Оно связывает полную поверхностную энергию с энергией Гиббса (поверхностное натяжение).
Для гетерогенной системы изменение внутренней энергии, исходя из I и II начал термодинамики:
dU =TdS – pdV + 

гдеdU — изменение внутренней энергии;
dS — изменение энтропии;
dV — изменение объема;

n — число молей компонента;
dq — изменение электрического заряда;


S — межфазная поверхность.
При S , V , n , q =const уравнение примет вид: dU = 

т.е. 
Из уравнений видно 



В случае твердых фаз процесс образования новой поверхности носит необратимый характер и 
Возможны два варианта:
1. 
Отсюда следует, что в дисперсных системах в самопроизвольных процессах поверхность (а, следовательно, и поверхностное натяжение) уменьшается.
🎥 Видео
Энергия Гиббса и Гельмгольца.Фугитивность и активность.Термодинамические потенциалы.Скачать

Урок 197. Поверхностная энергия. Коэффициент поверхностного натяженияСкачать

Поверхностные явления. Адсорбция.Скачать

Поверхностное натяжение (видео 3) | Силы межмолекулярного взаимодействия | ХимияСкачать
Химия | Тепловой эффект химической реакции (энтальпия)Скачать

Решение задач на вычисление энергии Гиббса. 1 часть. 10 класс.Скачать

Энергия Гиббса. Практическая часть. 10 класс.Скачать

Почему энергия Гиббса так важна ?Скачать

4.1. Поверхностное натяжениеСкачать

Физическая химия # 1. Полные дифференциалыСкачать
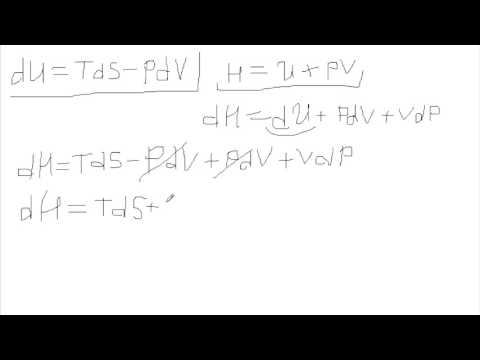
Адсорбция на поверхностях растворовСкачать

Поверхностное натяжениеСкачать

Лекция 87 Количественное описание адсорбцииСкачать

Поверхностные явления: адгезия, смачивание, адсорбция | Коллоидная химияСкачать


































