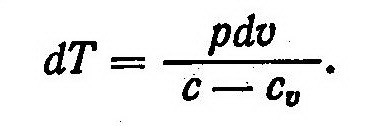• Воспользовавшись записью первого начала термодинамики в дифференциальной форме (9.2), получим выражение для теплоёмкости произвольного процесса:
• Представим полный дифференциал внутренней энергии через частные производные по параметрам 
После чего формулу (9.6) перепишем в виде
Соотношение (9.7) имеет самостоятельное значение, поскольку определяет теплоёмкость 
• Рассмотрим процесс при постоянном давлении 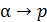
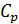
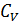
Исходя из полученной формулы, можно легко найти связь между теплоемкостями 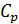
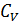
Уравнение Роберта Майера
Выразим частные производные в правой части уравнения (9.8), с помощью термического и калорического уравнений, записанных для одного моля идеального газа. Внутренняя энергия идеального газа зависит только от температуры и не зависит от объёма газа, следовательно
Из термического уравнения легко получить
Подставим (9.9) и (9.10) в (9.8), тогда
Вы, надеюсь, узнали (9.11). Да, конечно, это уравнение Майера. Еще раз напомним, что уравнение Майера справедливо только для идеального газа.
9.3. Политропические процессы в идеальном газе
Как отмечалось выше первое начало термодинамики можно использовать для вывода уравнений процессов, происходящих в газе. Большое практическое применение находит класс процессов, называемых политропическими. Политропическим называется процесс, проходящий при постоянной теплоемкости 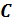
Уравнение процесса задается функциональной связью двух макроскопических параметров, описывающих систему. На соответствующей координатной плоскости 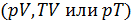
Вывод уравнения политропического процесса в идеальном газе
• Требование постоянства теплоёмкости 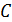
• Используя уравнение Майера (9.11) и уравнение состояния идеального газа, получаем следующее выражение для
• Разделив уравнение (9.12) на T и подставив в него (9.13) придем к выражению
• Разделив ( 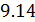
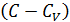
• Интегрированием (9.15), получаем
Это уравнение политропы в переменных
Исключая из уравнения ( 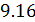

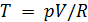
Параметр 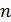
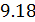
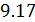
К этому классу процессов относится также адиабатный или адиабатический процесс. Адиабатным называется процесс, проходящий без теплообмена ( 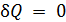
Из определения теплоемкости следует, что в адиабатическом процессе 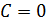
где 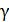
В этом случае уравнение политропы принимает вид
Уравнение адиабатного процесса (9.20) называют также уравнением Пуассона, поэтому параметр 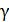
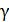
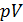
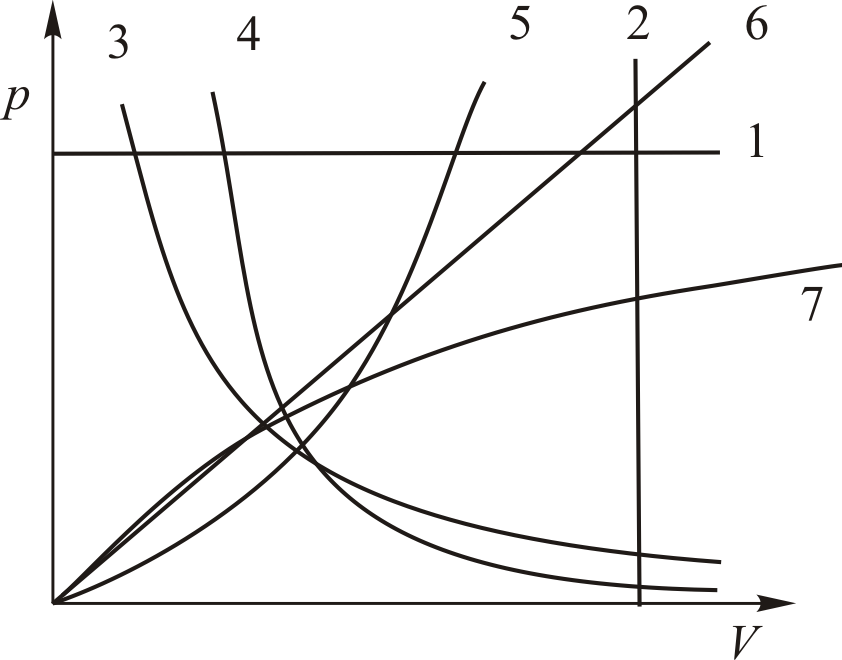
Графики политропических процессов для различных значений 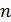
На рис. 9.1 графики процессов пронумерованы в соответствии с табл. 9.1.
| Номер политропы на рис. 9.1 | Значение показателя политропы | Уравнение политропы ( 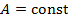 ) ) | Название процесса |
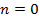 | 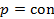 st st | изобарический | |
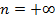 | 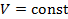 | изохорический | |
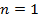 | 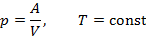 | изотермический | |
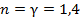 | 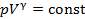 | адиабатический | |
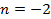 | 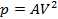 | — | |
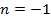 | 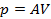 | — | |
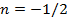 | 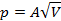 | — |
Знание показателя политропы 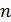
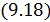
Тогда, бесконечно малое количество теплоты, сообщённое макросистеме в политропическом процессе равно
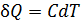
Соответственно полное количество теплоты, полученное системой при изменении её температуры от 

Зная 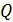
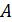
Таким образом, мы можем получить исчерпывающую информацию об энергообмене системы с окружающей средой.
Теперь уместно поставить следующие вопросы. Что делать, если процесс не политропический? Можно ли глядя на график процесса, догадаться, что это не политропа?
Иногда можно. Взгляните на рис. 9.2. Это уж точно не политропы.
Для подобных процессов количество теплоты рассчитать не так просто как в случае политропных процессов 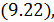
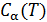
Полное количество теплоты, полученное системой в произвольном процессе, можно рассчитать только интегрированием
Вычисление теплоемкости и количества теплоты в различных процессах является внутренней подзадачей многих учебных задач, с которыми вы встретитесь при изучении термодинамики.
9.4. Тепловые машины и их эффективность.
Циклические процессы являются основой действия тепловых машин. В используемых на практике разнообразных тепловых машинах реализованы различные виды термодинамических циклов. Тепловыми машинами являются двигатели внутреннего сгорания, реактивные двигатели, холодильники, кондиционеры, тепловые насосы, паровые турбины и т. д.
| Рис. 9.3. |
Работа расширения 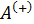
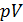
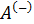
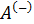
Действительно, проинтегрировав по циклу равенство, выражающее первое начало термодинамики, получим важный результат:
из которого следует, что работа равна количеству теплоты, полученной системой за цикл
Теплота в каких-то частях цикла поступает в систему ( 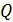
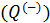
Определить поступает в систему количество теплоты или оно теряется иногда можно только расчётом, но зачастую это видно на графике процесса:
• Если температура 
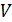
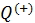
• Если температура 
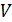
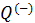
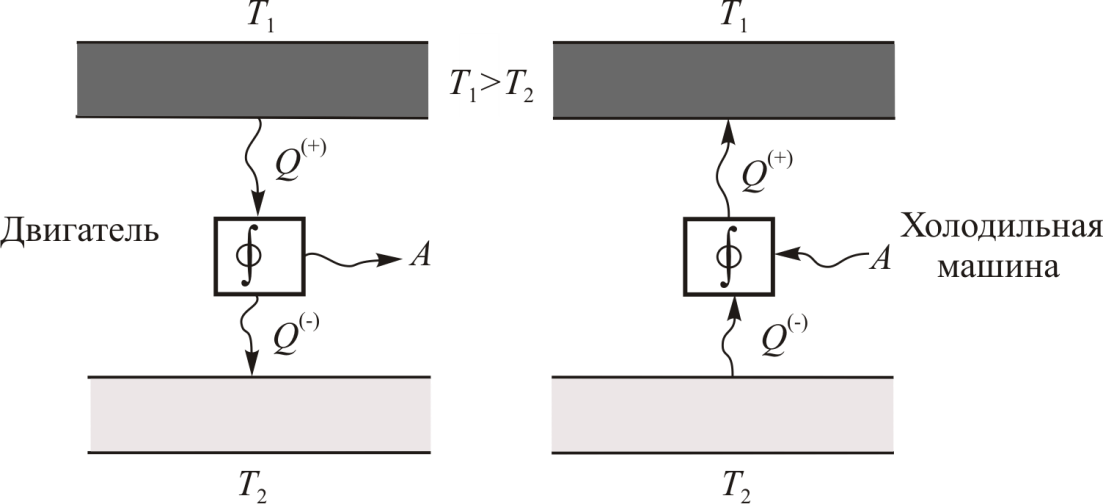
Принципиальная схема работы тепловой машины
Схематически работа машин по прямому и обращенному циклу представлена на рис. 9.4 и 9.5. Любая машина должна включать в себя нагреватель с температурой 

Принцип работы двигателя: в процессе работы машина получает количество теплоты от нагревателя, часть которого идёт на совершение полезной работы (приводится в действие какой-либо силовой агрегат), а часть отдаётся холодному резервуару.
Принцип работы холодильной машины: для того, чтобы отобрать количество теплоты от холодильника и передать его нагревателю, необходимо затратить некоторое количество энергии на совершение механической работы над рабочим веществом машины.
Показатели эффективности тепловых машин
Эффективность двигателя характеризуется коэффициентом полезного действия η (КПД). Эффективность холодильной машины – коэффициентом использования энергии ξ(КИЭ). На схеме 9.4.1 приведены формулы для вычисления КПД и КИЭ.
| Коэффициент полезного действия тепловой машины |
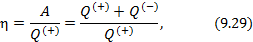  |
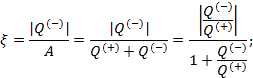 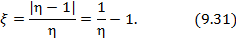 |
| Коэффициент использования энергии холодильной машины |
Чтобы воспользоваться формулами 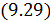
1. Сформулируйте первое начало термодинамики. Запишите его уравнение в дифференциальной форме, поясните обозначения бесконечно малых величин. К каким процессам применим этот постулат?
2. Что называется вечным двигателем первого рода?
3. Как определяются теплоемкости при постоянном объеме и при постоянном давлении? Почему их называют функциями состояния?
4. Получите уравнение, связывающее теплоемкости 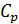
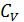
5. Сделайте вывод уравнения Майера. Для каких систем это уравнение применимо?
6. Что называется политропическим процессом? Запишите уравнение политропы для параметров
7. Как связан показатель политропы с теплоемкостью процесса?
8. Является ли адиабатный процесс политропическим процессом? Обоснуйте ответ.
9. Как выглядят графики политропических процессов? Приведите примеры.
10. Как можно определить работу, совершенную системой, через количество теплоты, полученное ею извне в политропическом процессе?
11. Нарисуйте принципиальные схемы тепловых машин, работающих как двигатель и как холодильная машина.
12. Дайте определения КПД и КИЭ. По каким формулам они вычисляются и как связаны между собой?
ТЕОРЕМЫ КАРНО И ИХ ПРИЛОЖЕНИЯ
В 1824 году французский физик и военный инженер Никола Леонар Сади Карно опубликовал свою работу «Размышления о движущей силе огня и о машинах, способных развивать эту силу», в которой им были сформулированы основные положения теории тепловых машин, содержащие по своей сути идею второго начала термодинамики.
В этом сочинении Карно ввёл в научный обиход множество понятий, использующихся в термодинамике и сейчас. Однако главной заслугой учёного стало выдвижение идей о необходимости перепада температур для создания циклически действующей тепловой машины и о том, что величина работы определяется только разностью температур нагревателя и холодильника и не зависит от природы рабочего вещества.
| Рис. 10.1. |
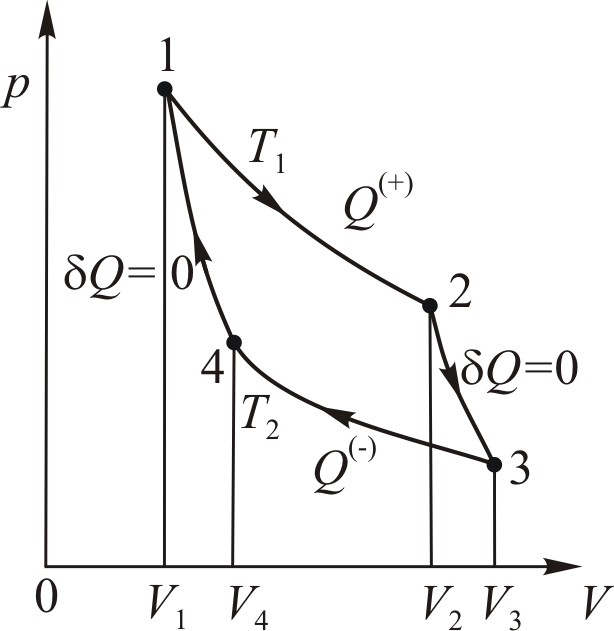
В идеальной машине Карно рабочее вещество (идеальный газ) совершает цикл, представленный на рис. 10.1, состоящий из двух изотерм и двух адиабат. Адиабата и изотерма слабо отличаются друг от друга, поэтому площадь внутри замкнутой кривой на диаграмме 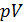
Расчёт КПД машины Карно
Идеальный газ совершает цикл, состоящий из двух изотерм и двух адиабат – цикл Карно, представленный на рис. 10.2.
Актуальная информация о системе и процессах
• Так как газ идеальный, то справедливо уравнение Клапейрона-Менделеева
• Изменение внутренней энергии идеального газа на изотерме равно нулю
• Уравнение адиабаты для идеального газа в параметрах 
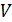
Рассчитать КПД тепловой машины Карно.
• По определению КПД двигателя равен
• Количество теплоты, поступающее к рабочему телу от нагревателя на
участке 1-2 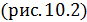
При записи (10.3) учтено, что изменение внутренней энергии идеального газа на изотерме не происходит.
• На участке 3-4 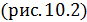

• На участках 2-3 и 4-1 рабочее тело изолируется от нагревателя и холодильника. Соответствующие квазистатические процессы идут без теплообмена
• Подставим в формулу (10.2) полученные значения 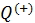
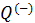
• Уравнение адиабатического процесса (10.1) позволяет существенно упростить это выражение. Действительно, для адиабаты 2 — 3 (рис. 10.2)
а для адиабаты 4 — 1 запишем
Если разделить уравнение (10.6) на уравнение (10.7), то получим
• Воспользовавшись этим результатом, из формулы (10.5) получим окончательный ответ
Из (10.9) видно, что чем ниже температура холодильника 



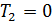

10.2. Теоремы Карно
Основные положения теории тепловых машин Сади Карно сформулировал в виде двух теорем, которые доказываются от противного [12]. Мы приведём лишь формулировки этих теорем и сфокусируем внимание на их приложениях (схема 10.2.1).
| Формулировки |
| Первая теорема Карно |
| Вторая теорема Карно |
| КПД тепловой машины, работающей по произвольному циклу с фиксированной максимальной и минимальной температурой, не превосходит КПД машины, работающей по циклу Карно с соответствующими температурами нагревателя и холодильника. |
| КПД машин, работающих по циклу Карно, не зависит от рабочего вещества и конструктивных особенностей машины, а определяется только температурами нагревателя и холодильника. |
| Приложения |
| • Построение абсолютной термодинамической шкалы температур. • Разработка метода теоретической термодинамики – метода циклов. |
| • Вывод неравенства Клаузиуса. • Определение энтропии в термодинамике. • Оценка эффективности тепловых машин сверху. |
Далее мы подробно рассмотрим каждое из приложений этих двух теорем. Начнем с построения абсолютной термодинамической шкалы температур.
Термодинамическая шкала температур
Поскольку КПД не зависит от рабочего тела, то можно представить следующую процедуру построения шкалы температур.
• В качестве нагревателя машины Карно берется некоторое стандартное тело, например, вода, кипящая при атмосферном давлении.
• В качестве холодильника выбирается другое стандартное тело, например лед, тающий при атмосферном давлении.
• Разность температур 

• Осуществляется обратимый цикл Карно с каким-либо телом.
• Измеряются 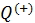
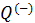
Кроме того 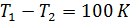




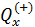
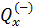
Отсюда находится искомая температура 
Построенная таким образом шкала температур Кельвина, как мы уже знаем, совпадает со шкалой газового термометра. Из уравнения (10.10) следует, что нулем температуры является температура, при которой 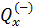
10.3. Метод циклов
С помощью первой теоремы Карно можно получить много важных соотношений между физическими величинами в дифференциальной форме, характеризующими систему в состоянии термодинамического равновесия. Для этого надо заставить систему надлежащим образом осуществить цикл Карно и применить к нему теорему Карно. Этот метод называется методом циклов. Проясним его сущность на примере решения следующей задачи.
Задача о нахождении зависимости внутренней энергии
макроскопического тела от его объема
Рассмотрим произвольное физически однородное тело, состояние которого характеризуется двумя параметрами 
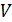
известно его термическое уравнение состояния
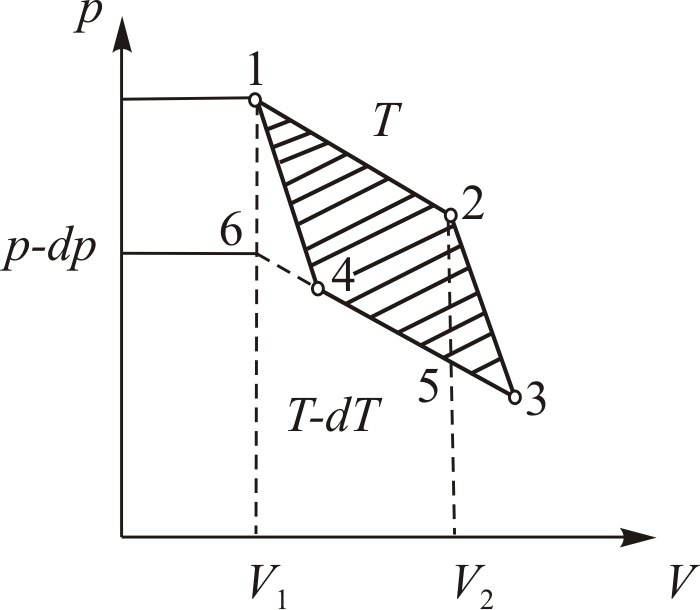
Для того, чтобы в соответствии с методом циклов получить зависимость энергии от объема в дифференциальной форме, необходимо осуществить бесконечно малый цикл Карно над рассматриваемым телом таким образом, чтобы температуры изотерм отличались на 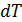

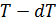
Запишем КПД цикла Карно с одной стороны через температуры, а с другой – через полученное телом количество теплоты и совершенную им работу
Работа 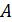
Высота этого параллелограмма численно равна приращению
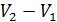
Основание же 6-1дает приращение давления при повышении температуры на 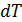
Для работы цикла, которая численно равна его площади, получаем
Вычислим теперь количество теплоты 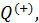
Так как на изотерме 1-2температура постоянна, то
Подставив (10.14) в (10.13), получим
Теперь вернемся к (10.11). Выразим числитель и знаменатель правой части этого уравнения согласно (10.12) и (10.15). Тогда получим
Из (10.16) легко выразить частную производную. В итоге получаем искомое решение
Подобным образом можно найти зависимость давления насыщенного пара от температуры или закон изменения поверхностного натяжения с температурой и множество других закономерностей.
10.4. Неравенство Клаузиуса. Определение энтропии
На основе второй теоремы Карно можно получить неравенство, связывающее приведённую теплоту нагревателя 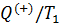
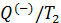
где 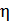


Запишем это неравенство более детально
или, что, то же самое
Знак минус в этом неравенстве показывает, что 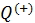
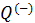
Отметим, что знак равенства относится к равновесному циклу Карно, а знак неравенства к неравновесному (необратимому).
Неравенство Клаузиуса можно обобщить для произвольного цикла [12]. Оно имеет следующий вид
здесь под 
Запишем (10.20) для произвольного обратимого цикла
Из этого следует (см. 8.1), что бесконечно малая величина под интегралом в (10.21) является полным дифференциалом некоторой функции состояния. Обозначим её буквой 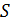
Равенство (10.22) определяет энтропию для обратимых процессов. Дальнейшему обсуждению этой важной термодинамической величины будет посвящена следующая лекция. Кроме того, свойства энтропии в окрестности абсолютного нуля температур мы рассмотрим при изучении третьего начала термодинамики.
10.5. Оценка эффективности тепловых машин сверху
В повседневной жизни мы постоянно используем различные виды тепловых машин. Наземные транспортные средства невозможно представить без бензинового двигателя внутреннего сгорания или дизельного мотора. На тепловых электростанциях работают паровые турбины. В небо нас уносят турбореактивные самолеты. В основе работы этих и многих других машин лежат различные циклические процессы и в них применяются разные рабочие вещества. У вас будет возможность научиться рассчитывать КПД и КИЭ на основе рассмотрения конкретных циклов Отто, Дизеля, Брайтона и других. Возникает вопрос, можно ли рассчитать показатели эффективности машины, не вдаваясь в детали ее работы. Оказывается можно, но, разумеется, приближенно. Вторая теорема Карно позволяет сделать оценки эффективности реальных машин сверху. Для этого нужно знать только максимальную температуру цикла машины 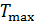
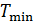
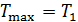
будем рассчитывать КПД и КИЭ реальных машин по формулам цикла Карно. Эти формулы приведены на схеме 10.5.1.
| Эффективность идеальной машины Карно |
| Коэффициент использования энергии |
| Коэффициент полезного действия |
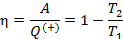 |
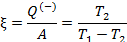 |
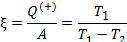 |
| Тепловой насос |
| Холодильник, кондиционер |
| Двигатель |
Примеры оценок эффективности тепловых машин сверху
КПД бензинового двигателя внутреннего сгорания




КПД реального теплового двигателя, работающего по циклу Отто, не превосходит 0,56.
Видео:30. Политропические процессыСкачать

Политропный процесс. Выведем уравнение политропного процесса
Читайте также:
|
 |
с=0; 
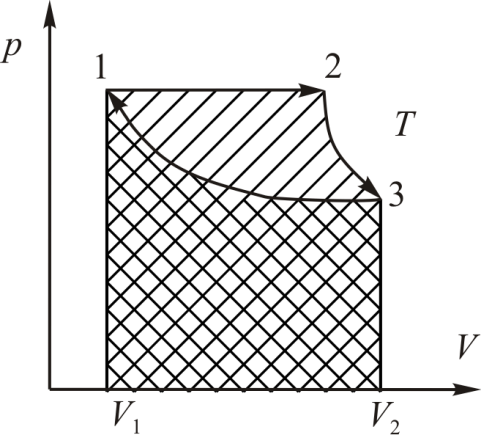
Если в координатах p, u выбрать произвольную точку А (рис. 4.9) и провести из т.А все рассмотренные выше процессы, а также сколько угодно других процессов, в которых показатель политропы меняется от +¥ до — ¥, то можно по графику процесса сказать о знаках работы, теплоты и изменения внутренней энергии, а также о знаке показателя n (как это показано на
рис. 4.9). Так, например, во всех процессах, исходящих из точки А и идущих правее адиабаты теплота, будет подводиться к рабочему телу q>0, а в противоположной области отводиться q
Дата добавления: 2015-01-19 ; просмотров: 37 ; Нарушение авторских прав
Видео:О.Я. Савченко 5.6.28* | Вывод уравнения политропыСкачать

Политропный процесс
Здравствуйте! В процессах изменения состояния газа переменными часто являются все параметры состояния (температура, давление, удельный объем), причем в некоторых процессах может изменяться и теплоемкость. Для того чтобы рассчитать такой процесс, необходимо знать зависимость теплоемкости от параметров процесса. Расчет значительно упрощается, если теплоемкость считать постоянной. Политропным называют процесс, происходящий при постоянной теплоемкости и вызываемый подводом тепла к рабочему телу или отводом тепла от него (название происходит от греческих слов «поли» — много и «тропос» — путь). В политропном процессе в общем случае могут изменяться все параметры и функции состояния.
Для вывода уравнения политропного процесса продифференцируем уравнение Клапейрона :
Из выражений dq=du+pdυ и du=cudT найдем
Подставив в это соотношение равенство dq = cdT, будем иметь
Из выражения (3) найдем
После подстановки этого равенства в выражение (1) получим
Величину газовой постоянной определим из уравнения Майера cp = cυ + R.
Подставив величину R в выражение (4), и выполнив некоторые преобразования, найдем
Разделив уравнение (5) на pυ и введя обозначение
Интегрирование этого выражения возможно при условии n = const, то есть c=const. После интегрирования уравнения (7) получим
Выражение (8) называют уравнением политропы. Оно определяет связь между параметрами состояния p и υ в политропном процессе. Величина n, которая находится из соотношения (6), называется показателем политропы. Показатель n является функцией теплоемкости и, как и теплоемкость зависит от характера процесса. Для анализа частных случаев процесса требуется знать соответствующий показатель политропы n.
При изохорном процессе (c=cυ) функция (6) претерпевает бесконечный разрыв, изменяясь от n = +∞ до n — ∞. При изобарном процессе (с = ср) показатель n = 0. Следовательно, показатель политропы n в зависимости от характера процесса может изменяться в широких пределах, принимая любые значения от —∞ до +∞.
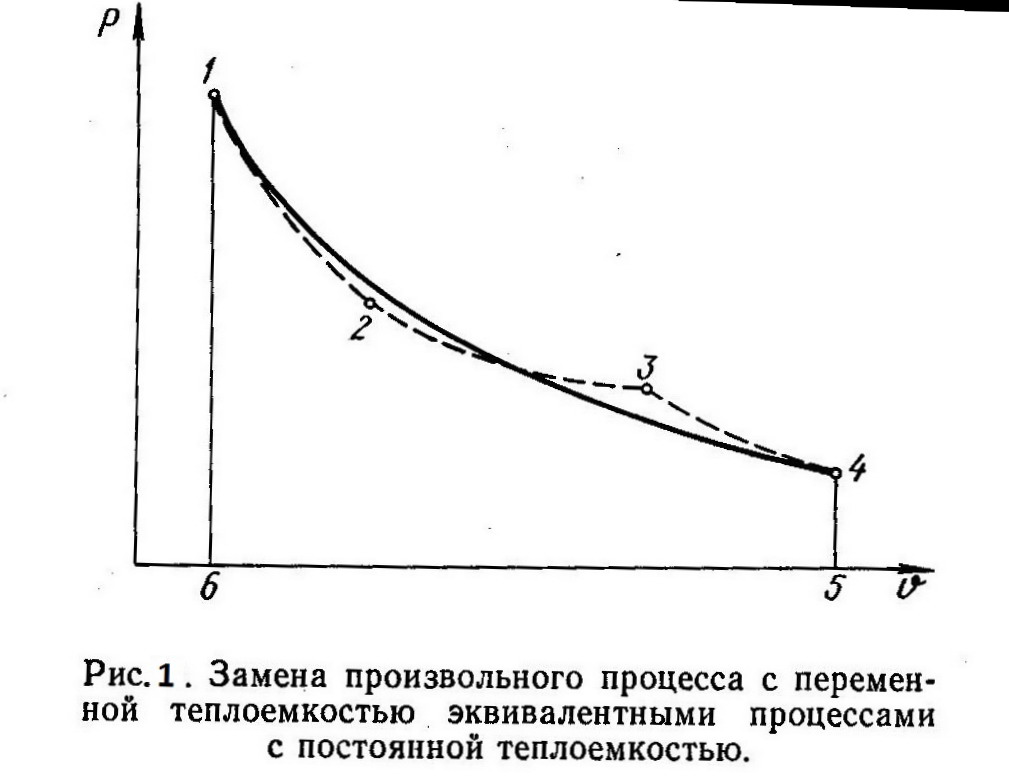
С помощью политропного процесса можно приближенно описать и рассчитать любой процесс изменения состояния 1—4 (рис. 1), для которого теплоемкость является переменной величиной. При этом произвольный процесс 1—4 необходимо заменить несколькими эквивалентными политропными процессами (процессы 1—2, 2—3 и 3—4), которые отличаются друг от друга постоянными значениями теплоемкости.
Замена должна производиться таким образом, чтобы работа в процессе 1—4 была равна работе на пути 1—2 — 3—4, то есть, чтобы были равны площади, ограниченные соответствующими кривыми процессов и ординатами 1—6 и 4—5. Так как изменение внутренней энергии ∆u на участке 1—4 не зависит от пути процесса (∆u=const), то, согласно уравнению q = ∆u + l первого закона термодинамики, количество теплоты в обоих случаях будет также одинаково. Погрешности, обусловленные такой заменой, окажутся тем меньшими, чем большим числом эквивалентных политропных участков будет заменен произвольный процесс 1—4, протекающий при переменной теплоемкости. Исп. литература: 1) Теплотехника, под общей ред. И.Н. Сушкина, Москва, «Металлургия», 1973. 2) Теплотехника, Бондарев В.А., Процкий А.Е., Гринкевич Р.Н. Минск, изд. 2-е,»Вышейшая школа», 1976.
🔥 Видео
Термодинамика Л3.1. Политропический процесс. Термодинамические циклы и КПДСкачать

Основы теплотехники. Термодинамические процессы. Изохорный, изобарный, изотермический, адиабатный.Скачать

Физика. Термодинамика: Адиабатный процесс. Центр онлайн-обучения «Фоксфорд»Скачать

Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Адиабатный процесс. 10 класс.Скачать

Политропный процессСкачать

Урок 178. Тепловые двигатели и их КПД. Цикл КарноСкачать

Политропический процессСкачать

Термодинамика Л3. 2022. Изопроцессы. Политропический процесс. Вращательные степени свободыСкачать

29. Адиабатический процесс. Уравнение ПуассонаСкачать

Выпуск 78. Политропный процесс. Решение задач по термодинамике.Скачать

ЧК_МИФ_ФМЛ_30 _ 2_2_5_3. ПОЛИТРОПНЫЕ ПРОЦЕССЫСкачать

Урок 167. Вычисление работы в термодинамикеСкачать

Урок 170. Количество теплоты. Первый закон термодинамикиСкачать

Адиабатный процесс. Практическая часть. 10 классСкачать

Термодинамика | уравнение МайераСкачать

Применение первого закона термодинамики к изопроцессам. 10 класс.Скачать

Семинар 7. Основы термодинамики.Скачать

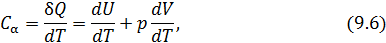
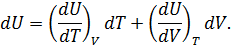
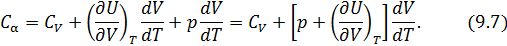
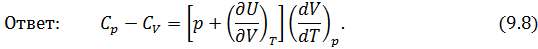

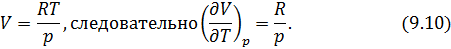
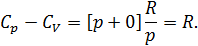


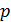

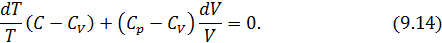
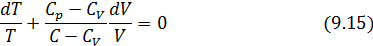

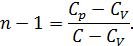
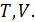
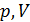




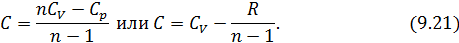

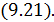
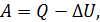
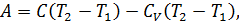
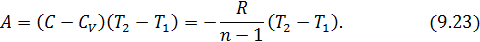
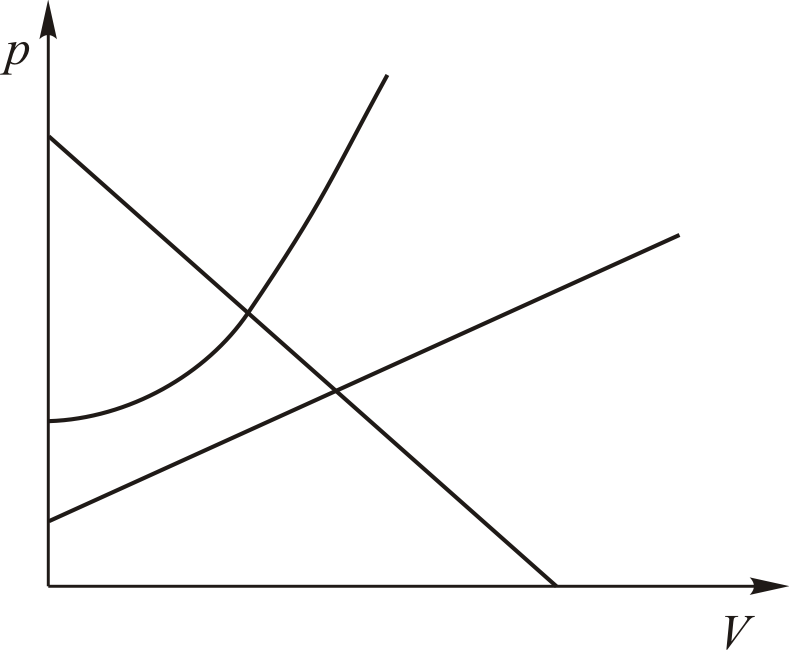

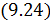

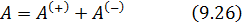
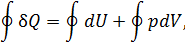
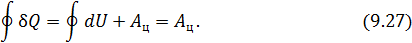

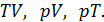

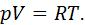
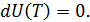


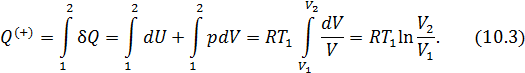
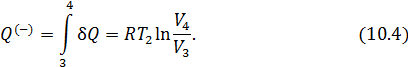
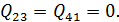
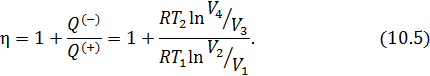


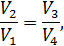



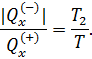
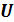
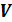
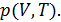

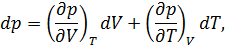
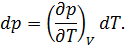
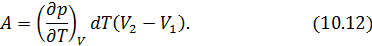
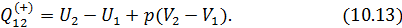

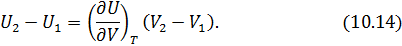
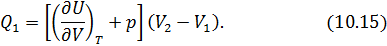
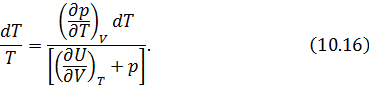
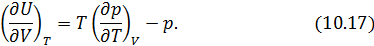
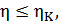
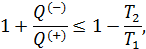





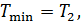
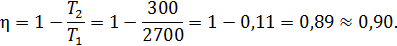
 . Обозначим
. Обозначим  — показатель политропы.
— показатель политропы. Проинтегрировав это уравнение, получим n ln u + ln p = const или ln pu n = const.
Проинтегрировав это уравнение, получим n ln u + ln p = const или ln pu n = const. ;
;  и
и  .
.
 , куда подставляют р = р1u1 n /v n , где p и u — текущие значения параметров.
, куда подставляют р = р1u1 n /v n , где p и u — текущие значения параметров. . (4.29)
. (4.29) , (4.30)
, (4.30) . (4.31)
. (4.31) . (4.32)
. (4.32) . (4.33)
. (4.33) . (4.34)
. (4.34) . Уравнение pu n = const представим в виде
. Уравнение pu n = const представим в виде  , тогда
, тогда  .
. ;
;  ;
; .
.