Полиномиальное относительно аргумента уравнение регрессии имеет (4 видео)

Полиномиальная регрессия

Полиномиальная регрессия означает приближение данных ( x_i , y_i ) полиномом k —й степени A ( x ) = a + b – x + c – x 2 + d – x 3 + . + h – x k . При k = 1 полином описывают прямой линией, при k = 2 – параболой, при k = 3 – кубической параболой и т.д. Как правило, на практике применяют k . Надо иметь в виду, что для построения регрессии полиномом k —й степени необходимо наличие по крайней мере ( k + l ) точек данных.

Чтобы осуществить полиномиальную регрессию с помощью MathCAD , надо выполнить следующие действия:

В главном меню необходимо выбрать «Вид – Панели инструментов – Матрица» , после чего в появившейся панели « Matrix » выбрать «Создать матрицу» на 1 строку и 7 столбцов и ввести координаты по оси x . Далее с помощью элемента «Транспонирование матрицы» той же панели транспонировать матрицу данных

х : = (0 1 2 3 4 5 6) Т .

Аналогичную операцию проводим с координатами по оси у

у : = (4,7 2,6 3,5 4,4 3,3 5,2 5,1) Т .

В MathCAD полиномиальная регрессия осуществляется комбинацией встроенной функции regress и полиномиальной интерполяции:

– regress ( х , у, k ) – вектор коэффициентов для построения полиномиальной регрессии данных;

– interp ( s , x , y , t ) – результат полиномиальной регрессии;

– х – вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;

– у – вектор действительных данных значений того же размера;

– k – степень полинома регрессии (целое положительное число);

– t – значение аргумента полинома регрессии.

Для построения полиномиальной регрессии после функции regress необходимо использовать функцию interp .

Далее записываем функцию полиномиальной регрессии как А ( t ): = interp ( s , x , y , t ).

Чтобы построить график, необходимо выбрать в главном меню «Вид – Панели инструментов – График» , далее на появившейся панели « Graph » выбрать элемент «Декартов график» , после чего на рабочей области программы MathCAD появится область построения графика. По оси ординат области построения графика необходимо ввести « A ( t ), y », а по оси абсцисс « t , x ». Далее двойным щелчком левой кнопки мыши по области построения графика необходимо вызвать панель форматирования графика, на которой выбрать закладку «Трассировки», выделить мышью « trace 2» и в поле «Символ» выбрать « dmnd ». Кроме того, для удобства можно установить диапазон значений по оси абсцисс, вводя соответствующие значения в области на оси x графика. Поскольку значения по оси х изменяются от 0 до 6, их и введём. Полученный график показан ниже.

Рис. Регрессия полиномом второй степени

Кроме того, мы можем рассчитать значение функции A ( t ) в требуемых точках. Например, для точки с аргументом x = 1,5 значение аппроксимирующей функции A ( t ) будет: A ( 1,5) = 3,553.

Содержание

Полиномиальная регрессия
Оглавление
Почему полиномиальная регрессия?
Компромисс против дисперсии
Применение полиномиальной регрессии к набору данных Housing
Вывод
Полиномиальное относительно аргумента уравнение регрессии имеет
🎦 Видео

Видео:Что такое полиномиальная регрессия? Душкин объяснитСкачать

Полиномиальная регрессия

Дата публикации Oct 8, 2018

Это мой третий блог в серии машинного обучения. Этот блог требует предварительных знаний о линейной регрессии. Если вы не знаете о линейной регрессии или нуждаетесь в обновлении, просмотрите предыдущие статьи этой серии.

Линейная регрессия требует, чтобы отношение между зависимой переменной и независимой переменной было линейным. Что если распределение данных было более сложным, как показано на рисунке ниже? Можно ли использовать линейные модели для подбора нелинейных данных? Как мы можем создать кривую, которая лучше всего отражает данные, как показано ниже? Что ж, мы ответим на эти вопросы в этом блоге.

Видео:Полиномиальная регрессияСкачать

Почему полиномиальная регрессия
Переоснащение против Подгонка
Уклон против Различий компромиссов
Применение полиномиальной регрессии к бостонскому набору данных.

Видео:Что такое линейная регрессия? Душкин объяснитСкачать

Почему полиномиальная регрессия?

Чтобы понять необходимость полиномиальной регрессии, давайте сначала сгенерируем случайный набор данных.

Сгенерированные данные выглядят как

Давайте применим модель линейной регрессии к этому набору данных.

Сюжет самой подходящей линии

Мы можем видеть, что прямая линия не может захватить шаблоны в данных. Это примерпод-фитинга, Вычисление RMSE и R²-показателя линейной линии дает:

Чтобы преодолеть несоответствие, нам нужно увеличить сложность модели.

Чтобы сгенерировать уравнение более высокого порядка, мы можем добавить мощности оригинальных функций в качестве новых. Линейная модель,

может быть преобразован в

Это все еще считаетсялинейная модельпоскольку коэффициенты / веса, связанные с признаками, все еще линейны. x² это только особенность. Однако кривая, которая нам подходитквадратныйв природе.

Для преобразования оригинальных функций в условия высшего порядка мы будем использовать PolynomialFeatures класс предоставлен scikit-learn , Далее мы обучаем модель с использованием линейной регрессии.

Подгонка модели линейной регрессии к преобразованным объектам дает график ниже.

Из графика совершенно ясно, что квадратичная кривая может соответствовать данным лучше, чем линейная линия. Вычисление RMSE и R²-балла квадратичного графика дает:

Мы можем видеть, что среднеквадратичное отклонение уменьшилось, а показатель R² увеличился по сравнению с линейной линией

Если мы попытаемся подогнать кубическую кривую (степень = 3) к набору данных, мы увидим, что он проходит через больше точек данных, чем квадратичный и линейный графики.

Метрика кубической кривой

Ниже приведено сравнение подгонки линейных, квадратичных и кубических кривых к набору данных.

Если мы продолжим увеличивать степень до 20, мы увидим, что кривая проходит через большее количество точек данных. Ниже приведено сравнение кривых для степени 3 и 20.

Для степени = 20 модель также фиксирует шум в данных. Это примернад-фитинга, Даже если эта модель проходит через большую часть данных, она не сможет обобщить невидимые данные.

Чтобы избежать перестройки, мы можем добавить больше обучающих выборок, чтобы алгоритм не распознавал шум в системе и мог стать более обобщенным.(Примечание: добавление дополнительных данных может быть проблемой, если данные сами по себе являются помехами).

Как выбрать оптимальную модель? Чтобы ответить на этот вопрос, нам нужно понять компромисс между компромиссом и дисперсией.

Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Компромисс против дисперсии

предвзятостьотносится к ошибке из-за упрощенных предположений модели при подборе данных. Высокое смещение означает, что модель не может захватить шаблоны в данных, и это приводит кпод-фитинга,

отклонениеотносится к ошибке из-за сложной модели, пытающейся соответствовать данным. Высокая дисперсия означает, что модель проходит через большинство точек данных, и это приводит кнад-фитингаданные.

На картинке ниже представлены результаты нашего обучения.

Из рисунка ниже мы можем наблюдать, что с увеличением сложности модели смещение уменьшается, а дисперсия увеличивается, и наоборот. В идеале модель машинного обучения должна иметьнизкая дисперсия и низкий уклон, Но практически невозможно иметь оба. Поэтому, чтобы получить хорошую модель, которая хорошо работает как на поездах, так и на невидимых данных,компромисссделан.

До сих пор мы рассмотрели большую часть теории полиномиальной регрессии. Теперь давайте реализуем эти концепции в наборе данных Boston Housing, который мы проанализировали впредыдущийблог.

Видео:Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

Применение полиномиальной регрессии к набору данных Housing

Из рисунка ниже видно, что LSTAT имеет небольшое нелинейное изменение с целевой переменной MEDV , Мы преобразуем исходные функции в полиномы более высокой степени, прежде чем обучать модель

Давайте определим функцию, которая преобразует исходные элементы в полиномиальные элементы заданной степени, а затем применяет к ним линейную регрессию.

Далее мы вызываем вышеуказанную функцию со степенью 2.

Производительность модели с использованием полиномиальной регрессии:

Это лучше, чем мы достигли с помощью линейной регрессии впредыдущийблог.

Вот и все для этой истории. Это GithubСделки рЕПОсодержит весь код для этого блога, и можно найти полный блокнот Jupyter, используемый для набора данных жилья в БостонеВот,

Видео:Множественная регрессияСкачать

Вывод

В этой серии машинного обучения мы рассмотрели линейную регрессию, полиномиальную регрессию и реализовали обе эти модели в наборе данных Boston Housing.

Мы расскажем о логистической регрессии в следующем блоге.

Видео:Линейная регрессия. Что спросят на собеседовании? ч.1Скачать

Полиномиальное относительно аргумента уравнение регрессии имеет

Модели нелинейной регрессии. Повысить точность оценок может позволить применение моделей нелинейной регрессии. Часто используют полиномиальные модели [c.90]

Сети нейронов высоких порядков Полиномиальная регрессия [c.202]

Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез. Как показывает опыт большинства исследователей, среди нелинейной полиномиальной регрессии чаще всего используется парабола второй степени в отдельных случаях — полином третьего порядка. Ограничения в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно менее однородна совокупность по результативному признаку. [c.63]

Хотя коэффициент детерминации по модели, параметры которой были рассчитаны обычным МНК, несколько выше, однако стандартные ошибки коэффициентов регрессии в модели, полученной с учетом ограничений на полиномиальную структуру лага, значительно снизились. Кроме того, модель, полученная обычным МНК, обладает более существенным недостатком коэффициенты регрессии при лаговых переменных этой модели xt и х, 3 нельзя считать статистически значимыми. [c.305]

Метод структурной минимизации риска может быть использован для восстановления регрессии в различных классах функций. Применим его для построения полиномиальной регрессии. [c.196]

Рис. 6.13. Истинная кусочно-линейная регрессия (—) и ее полиномиальная аппроксимация, полученная с помощью алгоритма структурной минимизации критерия адекватности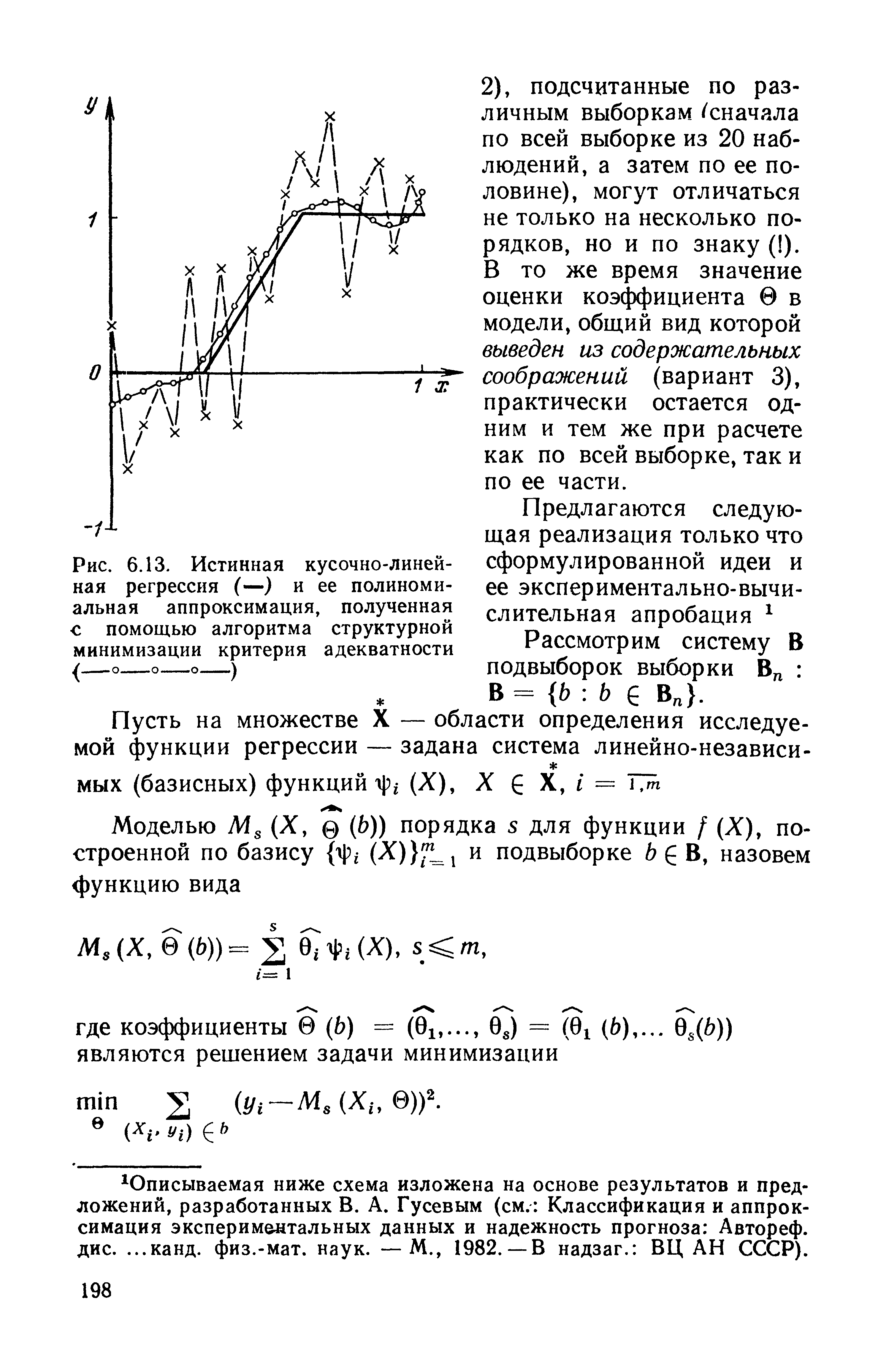

Полиномиальное относительно аргумента уравнение регрессии имеет

При проверке линейности регрессии (так Же, впрочем, как и при проверке гипотезы о полиномиальном характере регрессии заданного порядка т) в нормальных схемах зависимостей типа В и Сх описанный общий критерий является точным. При этом в линейном случае статистика у2, определенная соотношением (6.16), может быть выражена в более удобной форме, не требующей предварительного вычисления выборочной аппроксимирующей функции регрессии, а именно [c.203]

Когда истинный порядок полиномиальной регрессии не известен, то оценка параметров модели (7.18) проводится каж- [c.211]

Такая модель может быть получена, например, в полиномиальной регрессии при переходе к ортонормированной системе полиномов. В общей модели регрессии ортонормированными [c.262]

Полиномиальная регрессия. Рассмотрим случай скалярного (т. е. одномерного, р = 1) предиктора к, и пусть искомая функция регрессии / (х) принадлежит классу алгебраических полиномов степени т, т. е. [c.349]

Погрешность решения системы линейных уравнений 273 Полиномиальная регрессия 211, 349 Полиномы Чебышева 211, 327 Порядковые (ординальные) переменные 23, 99 [c.474]

Программа полиномиальной регрессии [c.180]

Многообразие и сложность экономических процессов предопределяет многообразие моделей, используемых для эконометрического анализа. С другой стороны, это существенно усложняет процесс нахождения максимально адекватной формулы зависимости. Для случая парной регрессии подбор модели обычно осуществляется по виду расположения наблюдаемых точек на корреляционном поле. Однако нередки ситуации, когда расположение точек приблизительно соответствует нескольким функциям и необходимо из них выявить наилучшую. Например, криволинейные зависимости могут аппроксимироваться полиномиальной, показательной, степенной, логарифмической функциями. Еще более неоднозначна ситуация для множествен- [c.189]

Здесь (11.5) — регрессия без ограничений, а (11.7) — регрессия с ограничениями.) В том случае, если значение F достаточно мало (меньше критического значения. F-статистики), модель полиномиальных лагов адекватна данным. Как обычно, при прочих равных условиях, надо выбирать модель с наименьшим количеством параметров. [c.267]

Полиномиальная регрессия выбирается, когда имеет место немонотонная зависимость между X и Y. Если на корреляционном поле есть только одна точка максимума или минимума, то выбирается квадратичная регрессия. [c.73]

Полиномиальная регрессия не может быть сведена с помощью замены переменных к линейной регрессии, поэтому для квадратичной модели надо пользоваться уравнениями (5.24). [c.74]

Построение линейных моделей. Осуществляется с использованием многомерной пошаговой регрессии и линейного варианта полиномиального алгоритма МГУА. Из полученных моделей была выбрана лучшая модель [c.322]

Пример. Дадим прогноз валового национального продукта США на 1979—1980 гг. в текущих ценах по данным4 за предшествующие 50 лет. Используем систему STADIA 5.O. Используя блок статистики системы и процедуру Простая регрессия (тренд) , получим оценки полиномиальной модели. Точность модели повышалась, пока степень полинома не достигла пятой [c.102]

IFPS имеет встроенный набор математических и статистических функций, в частности, функции линейной регрессии, линейной интерполяции, полиномиальной автокорреляции и скользящего среднего [c.314]

При сложных полиномиальных функциях с большим числом факторов необходимо помнить, что каждый параметр преобразованной функции является средней величиной, которая должна быть подсчитана по достаточному числу наблюдений. Если число наблюдений невелико, что, как правило, имеет место в эконометрике, то увеличение числа параметров функции приведет к их статистической незначимости и соответственно потребует упрощения вида функции. Если один и тот же фактор вводится в регрессию в разных степенях, то каждая степень рассматривается как самостоятельный фактор. Так, если модель имеет вид полинома второго порядка [c.104]

Рассмотрим общую модель с распределенным лагом, имеющую конечную максимальную величину лага /, которая описывается соотношением (7.3). Предположим, было установлено, что в исследуемой модели имеет место полиномиальная структура лага, т. е. зависимость коэффициентов регрессии Ь-, от величины лага описывается полиномом k-Pi степени. Частным случаем полиномиальной структуры лага является линейная модель (рис. 7.1 а)). Примерами лагов, образующих полином 2-й степени, явля- [c.298]

Некоторые вспомогательные преобразования, линеаризующие исследуемую парную зависимость. Часто при рассмотрении парных корреляционных полей ни линейная, ни полиномиальная регрессия не дают желаемой точности приближения. В этих случаях приходится обращаться к другим видам зависимостей гиперболической, степенной, показательной и др. Покажем, что в ряде ситуаций эти зависимости оказываются не менее удобными, чем линейная, поскольку легко к ней сводятся. [c.184]

В общем случае ответов на эти вопросы пока нет. Однако ориентиром может стать изучение модельных ситуаций. В частности, воспользуемся моделью засорения Шурыгина [14, п. 6.1.11]. В качестве основного распределения возьмем модель нормальной полиномиальной регрессии степени р, когда [c.221]

Случаи линейной (по предикторным переменным) и полиномиальной регрессии. Воспользуемся полученными в предыдущем пункте рекомендациями для анализа точности моделей линейной и полиномиальной регрессии. Нас будет интересовать, в частности, конкретизация формул (11.18 ) и (11.19) в этих случаях. [c.345]

Регрессионный анализ с помощью функции может выполнять простой, полиномиальный и анализ. Результат включает линейное уравнение регрессии, таблицу коэффициентов скорректированный таблицу ANOVA, таблицу соответствий и остатков, которые дали необычные наблюдения. Другие доступные характеристики включают ступенчатую регрессию, наилучшие подмножества, график подогнанной линии регрессии и диаграммы остатков. [c.675]

С учетом пяти форм полиномиальных уравнении тренда, можно получить девять форм уравнений регрессии. Речь идет только о трендах, т. е. об однофакторных моделях. (В Ex el, как известно, имеется также мощный инструментарий линейного многофакторного коррешвдионно-регресснонного моделирования.) [c.155]