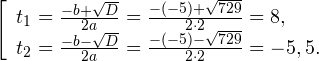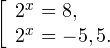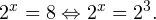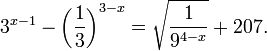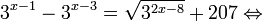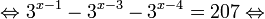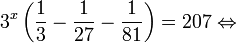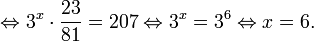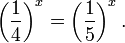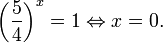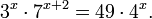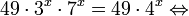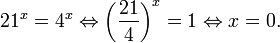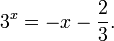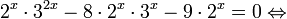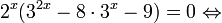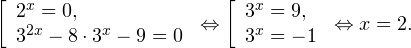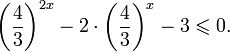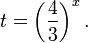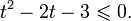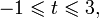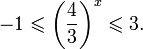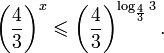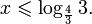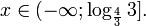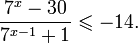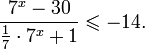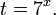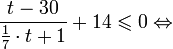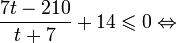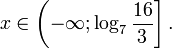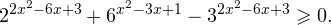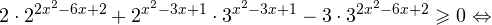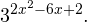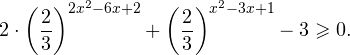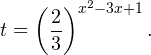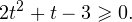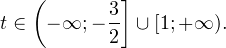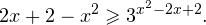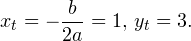О чем эта статья:
6 класс, 7 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать
Определение показательного уравнения
Показательными называются уравнения с показательной функцией f(x) = a х . Другими словами, неизвестная переменная в них может содержаться как в основании степени, так и в ее показателе. Простейшее уравнение такого вида: a х = b, где a > 0, a ≠ 1.
Конечно, далеко не все задачи выглядят так просто, некоторые из них включают тригонометрические, логарифмические и другие конструкции. Но для решения даже простых показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс следующие темы:
Если что-то успело забыться, советуем повторить эти темы перед тем, как читать дальнейший материал.
С точки зрения геометрии показательной функцией называют такую: y = a x , где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a
Иногда в результате решения будет получаться несколько вариантов ответа, и в таком случае мы должны выбрать тот корень, при котором показательная функция больше нуля.
Свойства степеней
Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут упрощать сложные показательные уравнения.
Видео:Показательные уравнения. 11 класс.Скачать
Показательная функция, ее свойства. Простейшие показательные уравнения
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На данном уроке мы рассмотрим показательную функцию, ее график и основные свойства. Также научимся решать простейшие показательные уравнения.
Если у вас возникнет сложность в понимании тему, рекомендуем посмотреть урок «Показательная функция и логарифм»
Видео:11 класс, 12 урок, Показательные уравненияСкачать
Показательные уравнения и неравенства
Решение большинства математических задач так или иначе связано с преобразованием числовых, алгебраических или функциональных выражений. Сказанное в особенности относится к решению показательных уравнений и неравенств. В вариантах ЕГЭ по математике к такому типу задач относится, в частности, задача C3. Научиться решать задания C3 важно не только с целью успешной сдачи ЕГЭ, но и по той причине, что это умение пригодится при изучении курса математики в высшей школе.
Выполняя задания C3, приходится решать различные виды уравнений и неравенств. Среди них — рациональные, иррациональные, показательные, логарифмические, тригонометрические, содержащие модули (абсолютные величины), а также комбинированные. В этой статье рассмотрены основные типы показательных уравнений и неравенств, а также различные методы их решений. О решении остальных видов уравнений и неравенств читайте в рубрике «Методическая копилка репетитора по физике и математике» в статьях, посвященных методам решения задач C3 из вариантов ЕГЭ по математике.
Прежде чем приступить к разбору конкретных показательных уравнений и неравенств, как репетитор по математике, предлагаю вам освежить в памяти некоторый теоретический материал, который нам понадобится.
Видео:Показательные уравнения. Практическая часть. 11 класс.Скачать
Показательная функция
Что такое показательная функция?
Функцию вида y = a x , где a > 0 и a ≠ 1, называют показательной функцией.
Основные свойства показательной функции y = a x :
| Свойство | a > 1 | 0 только в показателях каких-либо степеней. Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему: Помимо этого, полезно помнить об основных формулах и действиях со степенями:
Пример 1. Решите уравнение:
Решение: используем приведенные выше формулы и подстановку:
Уравнение тогда принимает вид:
Дискриминант полученного квадратного уравнения положителен:
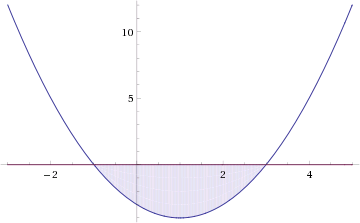
Это означает, что данное уравнение имеет два корня. Находим их:
Переходя к обратной подстановке, получаем:
Второе уравнение корней не имеет, поскольку показательная функция строго положительна на всей области определения. Решаем второе:
С учетом сказанного в теореме 1 переходим к эквивалентному уравнению: x = 3. Это и будет являться ответом к заданию. Ответ: x = 3. Пример 2. Решите уравнение:
Решение: ограничений на область допустимых значений у уравнения нет, так как подкоренное выражение имеет смысл при любом значении x (показательная функция y = 9 4 -x положительна и не равна нулю). Решаем уравнение путем равносильных преобразований с использованием правил умножения и деления степеней:
Последний переход был осуществлен в соответствии с теоремой 1. Пример 3. Решите уравнение:
Решение: обе части исходного уравнения можно поделить на 0,2 x . Данный переход будет являться равносильным, поскольку это выражение больше нуля при любом значении x (показательная функция строго положительна на своей области определения). Тогда уравнение принимает вид:
Ответ: x = 0. Пример 4. Решите уравнение:
Решение: упрощаем уравнение до элементарного путем равносильных преобразований с использованием приведенных в начале статьи правил деления и умножения степеней:
Деление обеих частей уравнения на 4 x , как и в предыдущем примере, является равносильным преобразованием, поскольку данное выражение не равно нулю ни при каких значениях x. Ответ: x = 0. Пример 5. Решите уравнение:
Решение: функция y = 3 x , стоящая в левой части уравнения, является возрастающей. Функция y = —x-2/3, стоящая в правой части уравнения, является убывающей. Это означает, что если графики этих функций пересекаются, то не более чем в одной точке. В данном случае нетрудно догадаться, что графики пересекаются в точке x = -1. Других корней не будет. Ответ: x = -1. Пример 6. Решите уравнение:
Решение: упрощаем уравнение путем равносильных преобразований, имея в виду везде, что показательная функция строго больше нуля при любом значении x и используя правила вычисления произведения и частного степеней, приведенные в начале статьи:
Ответ: x = 2. Видео:Как решать Показательные Уравнения? (часть 2)Скачать  Решение показательных неравенствПоказательными называются неравенства, в которых неизвестная переменная содержится только в показателях каких-либо степеней. Для решения показательных неравенств требуется знание следующей теоремы: Теорема 2. Если a > 1, то неравенство a f(x) > a g(x) равносильно неравенству того же смысла: f(x) > g(x). Если 0 f(x) > a g(x) равносильно неравенству противоположного смысла: f(x) 2x , при этом (в силу положительности функции y = 3 2x ) знак неравенства не изменится:
Тогда неравенство примет вид:
Итак, решением неравенства является промежуток:
переходя к обратной подстановке, получаем:
Левое неравенства в силу положительности показательной функции выполняется автоматически. Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству:
Поскольку в основании степени стоит число, большее единицы, эквивалентным (по теореме 2) будет переход к следующему неравенству:
Итак, окончательно получаем ответ:
Пример 8. Решите неравенство:
Решение: используя свойства умножения и деления степеней, перепишем неравенство в виде:
Введем новую переменную:
С учетом этой подстановки неравенство принимает вид:
Умножим числитель и знаменатель дроби на 7, получаем следующее равносильное неравенство:
Итак, неравенству удовлетворяют следующие значения переменной t:
Тогда, переходя к обратной подстановке, получаем:
Поскольку основание степени здесь больше единицы, равносильным (по теореме 2) будет переход к неравенству:
Окончательно получаем ответ:
Пример 9. Решите неравенство:
Решение:
Делим обе части неравенства на выражение:
Оно всегда больше нуля (из-за положительности показательной функции), поэтому знак неравенства изменять не нужно. Получаем:
Воспользуемся заменой переменной:
Исходное уравнение тогда принимает вид:
Итак, неравенству удовлетворяют значения t, находящиеся в промежутке:
Переходя к обратной подстановке получаем, что исходное неравенство распадается на два случая:
Первое неравенство решений не имеет в силу положительности показательной функции. Решаем второе:
Поскольку основание степени в данном случае оказалось меньше единицы, но больше нуля, равносильным (по теореме 2) будет переход к следующему неравенству:
Итак, окончательный ответ:
Пример 10. Решите неравенство:
Решение: Ветви параболы y = 2x+2-x 2 направлены вниз, следовательно она ограничена сверху значением, которое она достигает в своей вершине:
Ветви параболы y = x 2 -2x+2, стоящей в показателе, направлены вверх, значит она ограничена снизу значением, которое она достигает в своей вершине:
Вместе с этим ограниченной снизу оказывается и функция y = 3 x 2 -2x+2 , стоящая в правой части уравнения. Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 3 1 = 3. Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке x = 1. Ответ: x = 1. Для того, чтобы научиться решать показательные уравнения и неравенства, необходимо постоянно тренироваться в их решении. В этом нелегком деле вам могут помочь различные методические пособия, задачники по элементарной математике, сборники конкурсных задач, занятия по математике в школе, а также индивидуальные занятия с профессиональным репетитором. Искренне желаю вам успехов в подготовке и блестящих результатов на экзамене. P. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно. 🎥 ВидеоПО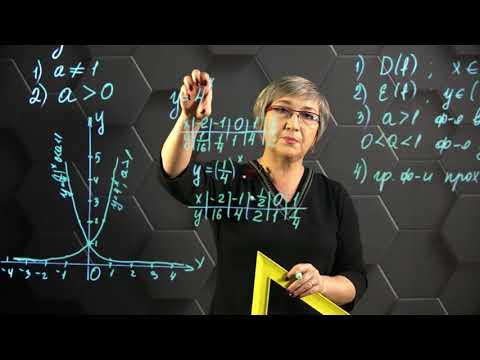КАЗАТЕЛЬНЫЕ УРАВНЕНИЯ😩 #математика #shorts #егэ #огэ #уравнение #показательныеуравненияСкачать  Показательная функция. 11 класс.Скачать  ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 10 класс решение показательных уравненийСкачать  Алгебра 10 класс (Урок№22 - Показательные уравнения. Системы показательных уравнений.)Скачать  Показательные уравнения — что это такое и как решатьСкачать  Показательные и логарифмические уравнения. Вебинар | МатематикаСкачать  Показательные уравнения за 50 минут | Математика ЕГЭ 10 класс | УмскулСкачать  Показательные уравнения. Видеоурок 11. Алгебра 10 классСкачать  Показательная функция | 10 класс АлимовСкачать  Показательные уравнения. Задание 13 | Математика ЕГЭ | УмскулСкачать  11 класс, 13 урок, Показательные неравенстваСкачать  11 класс, 11 урок, Показательная функция, её свойства и графикСкачать  Это просто! Как решать Показательные Неравенства?Скачать  Сложные показательные уравнения: примеры и способы решенияСкачать  Показательная функция. Видеоурок 10. Алгебра 10 классСкачать  |
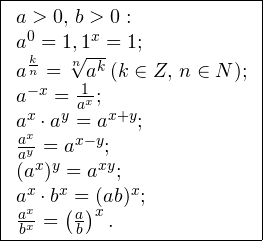0,, b>0: \ a^0 = 1, 1^x = 1; \ a^<frac>=sqrt[n]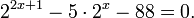 
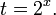
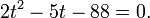
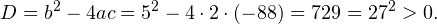0. ]» title=»Rendered by QuickLaTeX.com»/>
