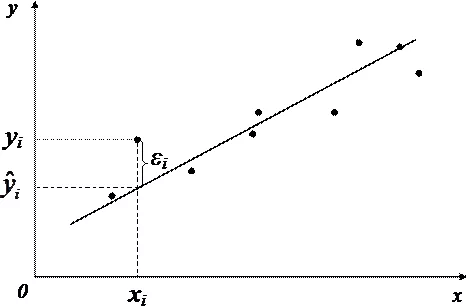
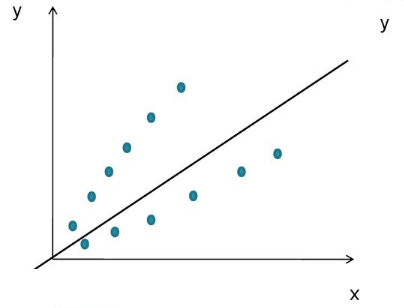
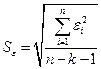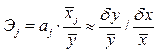Показатели качества уравнения регрессии в целом (8 видео)

Показатели качества регрессии

Качество модели регрессии связывают с адекватностью модели наблюдаемым (эмпирическим) данным. Проверка адекватности (или соответствия) модели регрессии наблюдаемым данным проводится на основе анализа остатков — .

Анализ остатков позволяет получить представление, насколько хорошо подобрана сама модель и насколько правильно выбран метод оценки коэффициентов. Согласно общим предположениям регрессионного анализа, остатки должны вести себя как независимые (в действительности, почти независимые) одинаково распределенные случайные величины.

Качество модели регрессии оценивается по следующим направлениям:

проверка качества всего уравнения регрессии;

проверка значимости всего уравнения регрессии;

проверка статистической значимости коэффициентов уравнения регрессии;

проверка выполнения предпосылок МНК.

При анализе качества модели регрессии, в первую очередь, используется коэффициент детерминации, который определяется следующим образом:

где — среднее значение зависимой переменной,

— предсказанное (расчетное) значение зависимой переменной.

Коэффициент детерминации показывает долю вариации результативного признака, находящегося под воздействием изучаемых факторов, т. е. определяет, какая доля вариации признака Y учтена в модели и обусловлена влиянием на него факторов.

Чем ближе 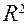к 1, тем выше качество модели.

Для оценки качества регрессионных моделей целесообразно также использовать коэффициент множественной корреляции (индекс корреляции) R

R = =

Данный коэффициент является универсальным, так как он отражает тесноту связи и точность модели, а также может использоваться при любой форме связи переменных.

Важным моментом является проверка значимости построенного уравнения в целом и отдельных параметров.

Оценить значимость уравнения регрессии – это означает установить, соответствует ли математическая модель, выражающая зависимость между Y и Х, фактическим данным и достаточно ли включенных в уравнение объясняющих переменных Х для описания зависимой переменной Y

Оценка значимости уравнения регрессии производится для того, чтобы узнать, пригодно уравнение регрессии для практического использования (например, для прогноза) или нет.

Для проверки значимости модели регрессии используется F-критерий Фишера. Если расчетное значение с n1= k и n2 = (n — k — 1) степенями свободы, где k – количество факторов, включенных в модель, больше табличного при заданном уровне значимости, то модель считается значимой.

В качестве меры точности применяют несмещенную оценку дисперсии остаточной компоненты, которая представляет собой отношение суммы квадратов уровней остаточной компоненты к величине (n- k -1), где k – количество факторов, включенных в модель. Квадратный корень из этой величины ( ) называется стандартной ошибкой:

значимость отдельных коэффициентов регрессии проверяется по t-статистике путем проверки гипотезы о равенстве нулю j-го параметра уравнения (кроме свободного члена):

где Saj — это стандартное (среднеквадратическое) отклонение коэффициента уравнения регрессии aj. Величина Saj представляет собой квадратный корень из произведения несмещенной оценки дисперсии и j -го диагонального элемента матрицы, обратной матрице системы нормальных уравнений.

где — диагональный элемент матрицы .

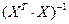
Если расчетное значение t-критерия с (n — k — 1) степенями свободы превосходит его табличное значение при заданном уровне значимости, коэффициент регрессии считается значимым. В противном случае фактор, соответствующий этому коэффициенту, следует исключить из модели (при этом ее качество не ухудшится).

Проверка выполнения предпосылок МНК.

Рассмотрим выполнение предпосылки гомоскедастичности, или равноизменчивости случайной составляющей (возмущения).

Невыполнение этой предпосылки, т.е. нарушение условия гомоскедастичности возмущений означает, что дисперсия возмущения зависит от значений факторов. Такие регрессионные модели называются моделями с гетероскедастичностью возмущений.

Обнаружение гетероскедастичности. Для обнаружения гетероскедастичности обычно используют тесты, в которых делаются различные предположения о зависимости между дисперсией случайного члена и объясняющей переменной: тест ранговой корреляции Спирмена, тест Голдфельда — Квандта, тест Глейзера, двусторонний критерий Фишера и другие [2].

При малом объеме выборки для оценки гетероскедастичности может использоваться метод Голдфельда — Квандта. Данный тест используется для проверки такого типа гетероскедастичности, когда дисперсия остатков возрастает пропорционально квадрату фактора. При этом делается предположение, что, случайная составляющая 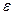распределена нормально.

Чтобы оценить нарушение гомоскедастичности по тесту Голдфельда — Квандта необходимо выполнить следующие шаги.

Упорядочение п наблюдений по мере возрастания переменной х.

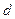
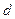
Исключение средних наблюдений ( должно быть примерно равно четверти общего количества наблюдений).

Разделение совокупности на две группы (соответственно с малыми и большими значениями фактора ) и определение по каждой из групп уравнений регрессии.

Определение остаточной суммы квадратов для первой регрессии и второй регрессии .

Вычисление отношений (или ). В числителе должна быть большая сумма квадратов.

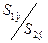
Полученное отношение имеет F распределение со степенями свободы k1=n1-k и k2=n-n1-k, (k– число оцениваемых параметров в уравнении регрессии).

Если , то гетероскедастичность имеет место.

Чем больше величина F превышает табличное значение F -критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин.

Оценка влияния отдельных факторов на зависимую переменную на основе модели (коэффициенты эластичности, b — коэффициенты).

Важную роль при оценке влияния факторов играют коэффициенты регрессионной модели. Однако непосредственно с их помощью нельзя сопоставить факторы по степени их влияния на зависимую переменную из-за различия единиц измерения и разной степени колеблемости. Для устранения таких различий при интерпретации применяются средние частные коэффициенты эластичности Э(j) и бета-коэффициенты b(j).

Эластичность Y по отношению к Х(j) определяется как процентное изменение Y, отнесенное к соответствующему процентному изменению Х. В общем случае эластичности не постоянны, они различаются, если измерены для различных точек на линии регрессии. По умолчанию стандартные программы, оценивающие эластичность, вычисляют ее в точках средних значений:

Эластичность ненормирована и может изменяться от — до + . Важно, что она безразмерна, так что интерпретация эластичности =2.0 означает, что если изменится на 1%, то это приведет к изменению на 2%. Если =-0.5, то это означает, что увеличение на 1% приведет к уменьшению на 0.5%.

Высокий уровень эластичности означает сильное влияние независимой переменной на объясняемую переменную.

где Sxj — среднеквадратическое отклонение фактора j

где .

Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении фактора j на один процент. Однако он не учитывает степень колеблемости факторов.

Бета-коэффициент показывает, на какую часть величины среднего квадратического отклонения Sy изменится зависимая переменная Y с изменением соответствующей независимой переменной Хj на величину своего среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных.

Указанные коэффициенты позволяют упорядочить факторы по степени влияния факторов на зависимую переменную.

Долю влияния фактора в суммарном влиянии всех факторов можно оценить по величине дельта — коэффициентов D (j):

где — коэффициент парной корреляции между фактором j (j = 1. m) и зависимой переменной.

В качестве основного литературного источника рекомендуется использовать [4], в качестве дополнительного – [2].

Содержание

Лекции по дисциплине «Эконометрика» (заочное отделение) (стр. 2 )
R — значит регрессия
Введение в регрессионный анализ
Линейная регрессия
Ограничения линейной регрессии
Как преодолеть эти ограничения
Линейная регрессия плюсов на Хабре
В заключение
🎦 Видео

Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Лекции по дисциплине «Эконометрика» (заочное отделение) (стр. 2 )

Показатели качества уравнения регрессии в целом

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4

Параметр формально является значением Y при X = 0. Он может не иметь экономического содержания. Интерпретировать можно лишь знак при параметре . Если > 0, то относительное изменение результата происходит медленнее, чем изменение фактора. Иными словами, вариация по фактору X выше вариации для результата Y. Также считают, что включает в себя неучтенные в модели факторы.

По итогам 2008 года были собраны данные по прибыли и оборачиваемости оборотных средств 500 торговых предприятий г. Челябинска. Результаты наблюдения сведены в таблицу.

Годовая прибыль предприятия, млн. руб.

Годовая оборачиваемость оборотных средств, раз

Требуется построить зависимость прибыли предприятий от оборачиваемости оборотных средств и оценить качество полученного уравнения.

Пусть y – прибыль предприятия, x – оборачиваемость оборотных средств.

На основе исходных данных были рассчитаны следующие показатели:

Уровень доверия возьмем q=0,95 или 95%.

1. Стандартные ошибки оценок , . намного больше =0,39, следовательно, низкая точность коэффициента . очень мала по сравнению с , следовательно, высокая точность коэффициента .

2. Интервальные оценки коэффициентов уравнения регрессии.

n – 2 = 500 – 2 = 498;

α: → → очень низкая точность коэффициента;

β: → → высокая точность коэффициента.

3. Значимость коэффициентов регрессии.

= >1,96 → коэффициент значим;

= >1,96 → коэффициент значим.

4. Стандартная ошибка регрессии. Se=0,91, по сравнению со средним значением =34,5 ошибка невысокая, точность уравнения хорошая.

5. Коэффициент детерминации. R2 = rxy2=0,782=0,6084 не очень близко к 1, качество подгонки среднее.

6. Средняя ошибка аппроксимации. A=11%, качество подгонки уравнения среднее.

Экономическая интерпретация: при увеличении оборачиваемости оборотных средств предприятия на 1 раз в год средняя годовая прибыль увеличится на 5,86 млн. руб.

Тема 6. Нелинейная парная регрессия

Часто на практике между зависимой и независимыми переменными существует нелинейная форма взаимосвязи. В этом случае существует два выхода:

1) подобрать к анализируемым переменным преобразование, которое бы позволило представить существующую зависимость в виде линейной функции;

2) применить нелинейный метод наименьших квадратов.

Основные нелинейные регрессионные модели и приведение их к линейной форме

1. Экспоненциальное уравнение .

Если прологарифмировать левую и правую части данного уравнения, то получится

Это уравнение является линейным, но вместо y в левой части стоит ln y.

В данном случае параметр β1 имеет следующий экономический смысл: при увеличении переменной x на единицу переменная y в среднем увеличится примерно на 100·β% (более точно: y увеличится в раз).

2. Логарифмическое уравнение .

Переход к линейному уравнению осуществляется заменой переменной x на X=lnx..

Параметр β1 имеет следующий экономический смысл: для увеличения y на единицу необходимо увеличить переменную x в раз, т. е. примерно на .

3. Гиперболическое уравнение .

В этом случае необходимо сделать замену переменных x на . Для гиперболической зависимости нет простой интерпретации коэффициента регрессии β1.

4. Степенное уравнение .

Прологарифмировав левую и правую части данного уравнения, получим

Заменив соответствующие ряды их логарифмами, получится линейная регрессия.

Экономический смысл параметра β1: если значение переменной x увеличить на 1%, то y увеличится на β1%.

5. Показательное уравнение (β1>0, β1≠1).

Прологарифмировав левую и правую части уравнения, получим

Проведя замены Y=ln y и B1=ln β1, получится линейная регрессия.

Экономический смысл параметра β1: при увеличении переменной x на единицу переменная y в среднем увеличится в β1 раз.

Тема 7. Множественная линейная регрессия: определение и оценка параметров

1. Понятие множественной линейной регрессии

Модель множественной линейной регрессии является обобщением парной линейной регрессии и представляет собой следующее выражение:

, t=1. n,

где yt – значение зависимой переменной для наблюдения t,

xit – значение i-й независимой переменной для наблюдения t,

εt – значение случайной ошибки для наблюдения t,

n – число наблюдений,

m – число независимых переменных x.

2. Матричная форма записи множественной линейной регрессии

Уравнение множественной линейной регрессии можно записать в матричной форме:

где , , , .

3. Основные предположения

2. для всех наблюдений;

3. = const для всех наблюдений;

4. ;

В случае выполнения вышеперечисленных гипотез модель называется нормальной линейной регрессионной.

4. Метод наименьших квадратов

Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов (МНК): .

Чтобы найти минимум этой функции необходимо вычислить производные по каждому из параметров и приравнять их к нулю, в результате получается система уравнений, решение которой в матричном виде следующее:

→ .

5. Теорема Гаусса-Маркова

Если выполнены предположения 1-5 из пункта 3, то оценки , полученные методом наименьших квадратов, имеют наименьшую дисперсию в классе линейных несмещенных оценок, то есть являются несмещенными, состоятельными и эффективными.

Тема 8. Множественная линейная регрессия: оценка качества

1. Общая схема проверки качества парной регрессии

Адекватность модели – остатки должны удовлетворять условиям теоремы Гаусса-Маркова.

Основные показатели качества коэффициентов регрессии:

1. Стандартные ошибки оценок (анализ точности определения оценок).

2. Интервальные оценки коэффициентов уравнения регрессии (построение доверительных интервалов).

3. Значимость коэффициентов регрессии (проверка гипотез относительно коэффициентов регрессии).

Основные показатели качества уравнения регрессии в целом:

1. Стандартная ошибка регрессии Se (анализ точности уравнения регрессии).

2. Значимость уравнения регрессии в целом (проверка гипотезы относительно всех коэффициентов регрессии).

3. Коэффициент детерминации R2 (проверка качества подгонки уравнения к исходным данным).

4. Скорректированный коэффициент детерминации R2adj (проверка качества подгонки уравнения к исходным данным).

5. Средняя ошибка аппроксимации (проверка качества подгонки уравнения к эмпирическим данным).

2. Стандартные ошибки оценок

Стандартные ошибки коэффициентов регрессии – это средние квадратические отклонения коэффициентов регрессии от их истинных значений.

где

— диагональные элементы матрицы ,

Стандартная ошибка является оценкой среднего квадратического отклонения коэффициента регрессии от его истинного значения. Чем меньше стандартная ошибка тем точнее оценка.

3. Интервальные оценки коэффициентов множественной линейной регрессии

Доверительные интервалы для коэффициентов регрессии определяются следующим образом:

1. Выбирается уровень доверия q (0,9; 0,95 или 0,99).

2. Рассчитывается уровень значимости g = 1 – q.

3. Рассчитывается число степеней свободы n – m – 1, где n – число наблюдений, m – число независимых переменных.

4. Определяется критическое значение t-статистики (tкр) по таблицам распределения Стьюдента на основе g и n – m – 1.

5. Рассчитывается доверительный интервал для параметра :

Доверительный интервал показывает, что истинное значение параметра с вероятностью q находится в данных пределах.

Чем меньше доверительный интервал относительно коэффициента, тем точнее полученная оценка.

4. Значимость коэффициентов регрессии

Процедура оценки значимости коэффициентов осуществляется аналогичной парной регрессии следующим образом:

1. Рассчитывается значение t-статистики для коэффициента регрессии по формуле .

2. Выбирается уровень доверия q ( 0,9; 0,95 или 0,99).

3. Рассчитывается уровень значимости g = 1 – q.

4. Рассчитывается число степеней свободы n – m – 1, где n – число наблюдений, m – число независимых переменных.

5. Определяется критическое значение t-статистики (tкр) по таблицам распределения Стьюдента на основе g и n – m – 1.

6. Если , то коэффициент является значимым на уровне значимости g. В противном случае коэффициент не значим (на данном уровне g).

t-тесты обеспечивают проверку значимости предельного вклада каждой переменной при допущении, что все остальные переменные уже включены в модель.

5. Стандартная ошибка регрессии

Стандартная ошибка регрессии Se показывает, насколько в среднем фактические значения зависимой переменной y отличаются от ее расчетных значений

Используется как основная величина для измерения качества модели (чем она меньше, тем лучше).

Значения Se в однотипных моделях с разным числом наблюдений и (или) переменных сравнимы.

6. Оценка значимости уравнения регрессии в целом

Уравнение значимо, если есть достаточно высокая вероятность того, что существует хотя бы один коэффициент, отличный от нуля.

Имеются альтернативные гипотезы:

Если принимается гипотеза H0, то уравнение статистически незначимо. В противном случае говорят, что уравнение статистически значимо.

Значимость уравнения регрессии в целом осуществляется с помощью F-статистики.

Оценка значимости уравнения регрессии в целом основана на тождестве дисперсионного анализа:

TSS – общая сумма квадратов отклонений

ESS – объясненная сумма квадратов отклонений

RSS – необъясненная сумма квадратов отклонений

F-статистика представляет собой отношение объясненной суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на одну степень свободы)

n – число выборочных наблюдений, m – число независимых переменных.

При отсутствии линейной зависимости между зависимой и независимой переменными F-статистика имеет F-распределение Фишера-Снедекора со степенями свободы k1 = m, k2 = n – m –1.

Процедура оценки значимости уравнения осуществляется следующим образом:

7. Рассчитывается значение F-статистики по формуле .

8. Выбирается уровень доверия q ( 0,9; 0,95 или 0,99).

9. Рассчитывается уровень значимости g = 1 – q.

10. Рассчитывается число степеней свободы n – m – 1, где n – число наблюдений, m – число независимых переменных.

11. Определяется критическое значение F-статистики (Fкр) по таблицам распределения Фишера на основе g и n – m – 1.

12. Если , то уравнение является значимым на уровне значимости g. В противном случае уравнение не значимо (на данном уровне g).

В парной регрессии F-статистика равна квадрату t-статистики: , а значимость коэффициента регрессии и значимость уравнения в целом эквивалентны.

Качество оценки уравнения можно проверить путем расчета коэффициента детерминации R2, который показывает степень соответствия найденного уравнения экспериментальным данным.

Коэффициент R2 показывает долю дисперсии переменной y, объясненную регрессией, в общей дисперсии y.

Коэффициент детерминации лежит в пределах 0 £ R2 £ 1.

Чем ближе R2 к 1, тем выше качество подгонки уравнения к статистическим данным.

Чем ближе R2 к 0, тем ниже качество подгонки уравнения к статистическим данным.

Коэффициенты R2 в разных моделях с разным числом наблюдений и переменных несравнимы.

8. Скорректированный коэффициент детерминации R2adj

Низкое значение R2 не свидетельствует о плохом качестве модели, и может объясняться наличием существенных факторов, не включенных в модель

R2 всегда увеличивается с включением новой переменной. Поэтому его необходимо корректировать, и рассчитывают скорректированный коэффициент детерминации

Если R2adj выходит за пределы интервала [0;1], то его использовать нельзя.

Если при добавлении новой переменной в модель увеличивается не только R2, но и R2adj, то можно считать, что вклад этой переменной в повышение качества модели существенен.

9. Средняя ошибка аппроксимации

Средняя ошибка аппроксимации (средняя абсолютная процентная ошибка) – показывает в процентах среднее отклонение расчетных значений зависимой переменной от фактических значений yi

Если A ≤ 10%, то качество подгонки уравнения считается хорошим. Чем меньше значение A, тем лучше.

10. Использование показателей качества коэффициентов и уравнения регрессии для интерпретации и корректировки модели

В случае незначимости уравнения, необходимо устранить ошибки модели. Наиболее распространенными являются следующие ошибки:

— неправильно выбран вид функции регрессии;

— в модель включены незначимые регрессоры;

— в модели отсутствуют значимые регрессоры.

После устранения ошибок требуется заново оценить параметры уравнения и его качество, продолжая этот процесс до тех пор, пока качество уравнения не станет удовлетворительным. Если после поделанных процедур, мы не достигли требуемого уровня значимости, то необходимо устранять другие ошибки (спецификации, классификации, наблюдения и т. д., см. тему 3, п. 6).

11. Интерпретация множественной линейной регрессии

Коэффициент регрессии при переменной xi показывает, на сколько увеличится среднее значение зависимой переменной y при увеличении xi на 1, при условии постоянства других переменных.

В апреле 2006 года были собраны данные по стоимости 200 двухкомнатных квартир в Металлургическом районе г. Челябинска, их жилой площади, площади кухни и расстоянии до центра города (пл. Революции). Результаты наблюдения сведены в таблицу.

Видео:Простые показатели качества модели регрессии (R2, критерии Акаике и Шварца)Скачать

R — значит регрессия

Статистика в последнее время получила мощную PR поддержку со стороны более новых и шумных дисциплин — Машинного Обучения и Больших Данных. Тем, кто стремится оседлать эту волну необходимо подружится с уравнениями регрессии. Желательно при этом не только усвоить 2-3 приемчика и сдать экзамен, а уметь решать проблемы из повседневной жизни: найти зависимость между переменными, а в идеале — уметь отличить сигнал от шума.

Для этой цели мы будем использовать язык программирования и среду разработки R, который как нельзя лучше приспособлен к таким задачам. Заодно, проверим от чего зависят рейтинг Хабрапоста на статистике собственных статей.

Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Введение в регрессионный анализ

Если имеется корреляционная зависимость между переменными y и x , возникает необходимость определить функциональную связь между двумя величинами. Зависимость среднего значения называется регрессией y по x .

Основу регрессионного анализа составляет метод наименьших квадратов (МНК), в соответствии с которым в качестве уравнения регресии берется функция такая, что сумма квадратов разностей минимальна.

Карл Гаусс открыл, или точнее воссоздал, МНК в возрасте 18 лет, однако впервые результаты были опубликованы Лежандром в 1805 г. По непроверенным данным метод был известен еще в древнем Китае, откуда он перекочевал в Японию и только затем попал в Европу. Европейцы не стали делать из этого секрета и успешно запустили в производство, обнаружив с его помощью траекторию карликовой планеты Церес в 1801 г.

Вид функции , как правило, определен заранее, а с помощью МНК подбираются оптимальные значения неизвестных параметров. Метрикой рассеяния значений вокруг регрессии является дисперсия.

k — число коэффициентов в системе уравнений регрессии.

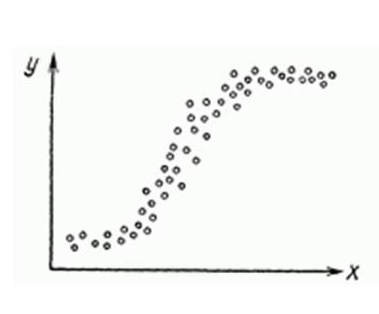
Чаще всего используется модель линейной регрессии, а все нелинейные зависимости приводят к линейному виду с помощью алгебраических ухищрений, различных преобразования переменных y и x .

Линейная регрессия

Уравнения линейной регрессии можно записать в виде

В матричном виде это выгладит

y — зависимая переменная;
x — независимая переменная;
β — коэффициенты, которые необходимо найти с помощью МНК;
ε — погрешность, необъяснимая ошибка и отклонение от линейной зависимости;

Случайная величина может быть интерпретирована как сумма из двух слагаемых:

— полная дисперсия (TSS).
— объясненная часть дисперсии (ESS).
— остаточная часть дисперсии (RSS).

Еще одно ключевое понятие — коэффициент корреляции R 2 .

Видео:Линейная регрессия. Оценка качества моделиСкачать

Ограничения линейной регрессии

Для того, чтобы использовать модель линейной регрессии необходимы некоторые допущения относительно распределения и свойств переменных.

Линейность, собственно. Увеличение, или уменьшение вектора независимых переменных в k раз, приводит к изменению зависимой переменной также в k раз.
Матрица коэффициентов обладает полным рангом, то есть векторы независимых переменных линейно независимы.
Экзогенность независимых переменных — . Это требование означает, что математическое ожидание погрешности никоим образом нельзя объяснить с помощью независимых переменных.
Однородность дисперсии и отсутствие автокорреляции. Каждая ε_i обладает одинаковой и конечной дисперсией σ 2 и не коррелирует с другой ε_i. Это ощутимо ограничивает применимость модели линейной регрессии, необходимо удостовериться в том, что условия соблюдены, иначе обнаруженная взаимосвязь переменных будет неверно интерпретирована.

Как обнаружить, что перечисленные выше условия не соблюдены? Ну, во первых довольно часто это видно невооруженным глазом на графике.

Неоднородность дисперсии

При возрастании дисперсии с ростом независимой переменной имеем график в форме воронки.

Нелинейную регрессии в некоторых случая также модно увидеть на графике довольно наглядно.

Тем не менее есть и вполне строгие формальные способы определить соблюдены ли условия линейной регрессии, или нарушены.

Автокорреляция проверяется статистикой Дарбина-Уотсона (0 ≤ d ≤ 4). Если автокорреляции нет, то значения критерия d≈2, при позитивной автокорреляции d≈0, при отрицательной — d≈4.
Неоднородность дисперсии — Тест Уайта, , при chi_$» data-tex=»inline»/> нулевая гипотеза отвергается и констатируется наличие неоднородной дисперсии. Используя ту же можно еще применить тест Бройша-Пагана.
Мультиколлинеарность — нарушения условия об отсутствии взаимной линейной зависимости между независимыми переменными. Для проверки часто используют VIF-ы (Variance Inflation Factor).

В этой формуле — коэффициент взаимной детерминации между и остальными факторами. Если хотя бы один из VIF-ов > 10, вполне резонно предположить наличие мультиколлинеарности.

Почему нам так важно соблюдение всех выше перечисленных условий? Все дело в Теореме Гаусса-Маркова, согласно которой оценка МНК является точной и эффективной лишь при соблюдении этих ограничений.

Видео:Парная регрессия: линейная зависимостьСкачать

Как преодолеть эти ограничения

Нарушения одной или нескольких ограничений еще не приговор.

Нелинейность регрессии может быть преодолена преобразованием переменных, например через функцию натурального логарифма ln .
Таким же способом возможно решить проблему неоднородной дисперсии, с помощью ln , или sqrt преобразований зависимой переменной, либо же используя взвешенный МНК.
Для устранения проблемы мультиколлинеарности применяется метод исключения переменных. Суть его в том, что высоко коррелированные объясняющие переменные устраняются из регрессии, и она заново оценивается. Критерием отбора переменных, подлежащих исключению, является коэффициент корреляции. Есть еще один способ решения данной проблемы, который заключается в замене переменных, которым присуща мультиколлинеарность, их линейной комбинацией. Этим весь список не исчерпывается, есть еще пошаговая регрессия и другие методы.

К сожалению, не все нарушения условий и дефекты линейной регрессии можно устранить с помощью натурального логарифма. Если имеет место автокорреляция возмущений к примеру, то лучше отступить на шаг назад и построить новую и лучшую модель.

Видео:Критерий Фишера для проверки адекватности построенной регрессииСкачать

Линейная регрессия плюсов на Хабре

Итак, довольно теоретического багажа и можно строить саму модель.
Мне давно было любопытно от чего зависит та самая зелененькая цифра, что указывает на рейтинг поста на Хабре. Собрав всю доступную статистику собственных постов, я решил прогнать ее через модель линейно регрессии.

Загружает данные из tsv файла.

points — Рейтинг статьи
reads — Число просмотров.
comm — Число комментариев.
faves — Добавлено в закладки.
fb — Поделились в социальных сетях (fb + vk).
bytes — Длина в байтах.

Вопреки моим ожиданиям наибольшая отдача не от количества просмотров статьи, а от комментариев и публикаций в социальных сетях. Я также полагал, что число просмотров и комментариев будет иметь более сильную корреляцию, однако зависимость вполне умеренная — нет надобности исключать ни одну из независимых переменных.

Теперь собственно сама модель, используем функцию lm .

В первой строке мы задаем параметры линейной регрессии. Строка points

. определяет зависимую переменную points и все остальные переменные в качестве регрессоров. Можно определить одну единственную независимую переменную через points

reads , набор переменных — points

Перейдем теперь к расшифровке полученных результатов.

Intercept — Если у нас модель представлена в виде , то тогда — точка пересечения прямой с осью координат, или intercept .
R-squared — Коэффициент детерминации указывает насколько тесной является связь между факторами регрессии и зависимой переменной, это соотношение объясненных сумм квадратов возмущений, к необъясненным. Чем ближе к 1, тем ярче выражена зависимость.
Adjusted R-squared — Проблема с в том, что он по любому растет с числом факторов, поэтому высокое значение данного коэффициента может быть обманчивым, когда в модели присутствует множество факторов. Для того, чтобы изъять из коэффициента корреляции данное свойство был придуман скорректированный коэффициент детерминации .
F-statistic — Используется для оценки значимости модели регрессии в целом, является соотношением объяснимой дисперсии, к необъяснимой. Если модель линейной регрессии построена удачно, то она объясняет значительную часть дисперсии, оставляя в знаменателе малую часть. Чем больше значение параметра — тем лучше.
t value — Критерий, основанный на t распределении Стьюдента . Значение параметра в линейной регрессии указывает на значимость фактора, принято считать, что при t > 2 фактор является значимым для модели.
p value — Это вероятность истинности нуль гипотезы, которая гласит, что независимые переменные не объясняют динамику зависимой переменной. Если значение p value ниже порогового уровня (.05 или .01 для самых взыскательных), то нуль гипотеза ложная. Чем ниже — тем лучше.

Можно попытаться несколько улучшить модель, сглаживая нелинейные факторы: комментарии и посты в социальных сетях. Заменим значения переменных fb и comm их степенями.

Проверим значения параметров линейной регрессии.

Как видим в целом отзывчивость модели возросла, параметры подтянулись и стали более шелковистыми , F-статистика выросла, так же как и скорректированный коэффициент детерминации .

Проверим, соблюдены ли условия применимости модели линейной регрессии? Тест Дарбина-Уотсона проверяет наличие автокорреляции возмущений.

И напоследок проверка неоднородности дисперсии с помощью теста Бройша-Пагана.

Видео:Эконометрика Линейная регрессия и корреляцияСкачать

В заключение

Конечно наша модель линейной регрессии рейтинга Хабра-топиков получилось не самой удачной. Нам удалось объяснить не более, чем половину вариативности данных. Факторы надо чинить, чтобы избавляться от неоднородной дисперсии, с автокорреляцией тоже непонятно. Вообще данных маловато для сколь-нибудь серьезной оценки.

Но с другой стороны, это и хорошо. Иначе любой наспех написанный тролль-пост на Хабре автоматически набирал бы высокий рейтинг, а это к счастью не так.