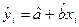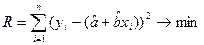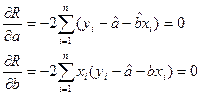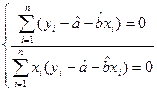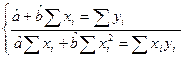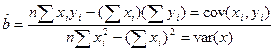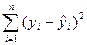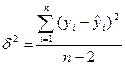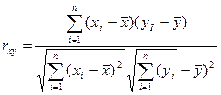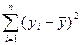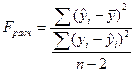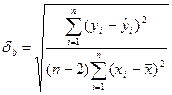Показатели качества подгонки для регрессионного уравнения (5 видео)

Однофакторное регрессионное уравнение

1. Понятие регрессионного уравнения.

2. Метод наименьших квадратов.

3. Проверка адекватности регрессионного уравнения.

3.1. Показатели качества подгонки.

3.2. Проверка различных гипотез относительно регрессионного уравнения.

3.3. «Хорошие» свойства оценок.

3.4. Экономический смысл коэффициентов регрессии.

1. Регрессионное уравнение модели отражает зависимость между экономическими переменными, а именно между одной зависимой (эндогенной) и одной или более независимыми (экзогенными) переменными. Зависимая переменная обозначается через «у», а независимая через «х».

Направление причинно-следственной связи между переменными определяется через предварительное обоснование и включается в модель как гипотеза.

Регрессионный анализ проверяет статистическую состоятельность модели при данной гипотезе.

Регрессионное уравнение может быть однофакторным и многофакторным. В первом случае одна переменная зависит от другой, во втором случае одна переменная зависит от нескольких других.

Регрессионное уравнение, которое отражает зависимость между математическим ожиданием (условным распределением) одной переменной и соответствующим значением другой переменной, называется однофакторным регрессионным уравнением.

В общем виде однофакторное регрессионное уравнение может быть записано в следующем виде:

₍₁₎

— условное математическое ожидание переменной Y при заданном значении переменной X.

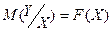
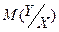
Частным случаем однофакторного регрессионного уравнения является линейная модель зависимости, которая записывается следующим образом:

y_i=a+bx_i+ (2)

y_i – объяснимая (зависимая) переменная;

x_i – объясняющая (независимая) переменная;

а – свободный член регрессии или постоянная;

b – коэффициент регрессии, отражает наклон линии, вдоль которой рассеяны данные наблюдения модели. Коэффициент регрессии может быть истолкован как показатель, характеризующий процентное изменение переменной, которым вызвано изменение значения х на единицу.

Если знак перед b положителен, то говорим, что переменные коррелированны положительно, при отрицательном знаке переменные отрицательно коррелированны.

– ошибка или так называемая случайная компонента. Наличие случайной компоненты обусловлено двумя основными причинами:

1. любая регрессионная модель является упрощением действительной, на самом деле есть другие параметры, от которых зависит y_i.

2. присутствуют ошибки измерений.

Необходимо различать кросс-секционную регрессию и регрессию временных рядов.

Кросс-секционная регрессия проверяет связь между переменными в определенный период времени. Например, зависимость между количеством работников предприятия и прибылью, полученной этим предприятием. Чтобы измерить эту связь мы должны собрать данные по численности работников за 1 период (например, год) и данные о размерах прибыли достаточно большого числа предприятий за тот же самый период.

Данные о прибылях компаний соответствовали бы зависимой переменной, а данные о количестве работников были бы независимыми переменными.

При анализе регрессии во временных рядах данные по каждой из переменных собираются в течение следующих друг за другом периодов времени.

Регрессионный анализ временных рядов позволяет установить взаимосвязь между переменными в среднем в течение того периода времени по которому имеются данные. Независимо от того проводится кросс-секционный анализ или анализ временных рядов, основные принципы положения регрессионного анализа остаются те же.

2.Для статистической проверки взаимозависимости между зависимой (у) и независимой (х) переменными, необходимо найти значения а, b, в выражении (2).

Метод оценки этих параметров должен быть таким, чтобы это были «хорошие» оценки.

Метод, используемый чаще других для нахождения параметров регрессионного уравнения и известный как метод наименьших квадратов дает наилучшие линейные несмещенные оценки. Метод называется так потому, что при расчете параметров линии с помощью этого метода минимизируются суммы квадратов значений ошибок .

Допустим на графике нанесены наблюдения о совокупных доходах семей (х) и расходах этих же семей на питание (y). Анализируя графики можно сделать следующие выводы:

1. Точки не лежат на одной кривой и можно только провести некоторую линию в непосредственной близости от всех этих точек.

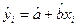
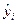
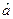
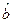
2. Можно сделать допущение, иными словами выдвинуть гипотезу, что доходы и расходы связаны линейной зависимостью, то есть можно построить некоторую прямую , отражающую зависимость между доходами и расходами, при этом значение назовем теоретически расчетными значениями зависимой переменной, а коэффициенты и – оценочными значениями коэффициентов а и b.

Для того, чтобы теоретическая прямая лежала в непосредственной близости от фактически наблюдаемых у_i необходимо минимизировать сумму квадратов отклонений между фактическими и расчетными значениями.

Разрыв скобки получим стандартную форму нормальных уравнений (для краткости опустим индексы у знаков сумм).

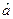
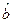
из этой системы находим и :

ковариация (cov) показывает тесноту связи

;

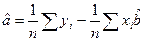
n – количество наблюдений.

Так рассчитываются величины регрессии.

Ошибка или случайная компонента находится как разница между расчетными значениями зависимой переменной и фактическими значениями:

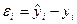
3. Адекватность регрессионного уравнения. То есть его соответствие реальному моделироваемому процессу, достоверность его параметров; исследуется с нескольких позиций:

1. Анализируются показатели качества подгонки регрессионного уравнения.

2. Проверяются различные гипотезы относительно параметров регрессионного уравнения.

3. Проверяется выполнение условий для получения «хороших» оценок МНК.

4. Производится содержательный анализ регрессионного уравнения.

3.1. Показатели качества подгонки отражают соотношение расчетных значений зависимой переменной 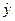с фактическими значениями зависимой переменной у.

Эти показатели как правило основываются на сумме квадратов разности этих показателей:

Первый из таких показателей – остаточная дисперсия.

Для однофакторного уравнения однофакторная дисперсия определяется по формуле:

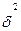
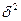
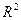
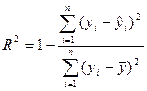
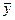
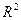
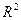
Чем меньше , тем лучше регрессионное уравнение, — является размерной величиной и сопоставление регрессионных уравнений по нему, отражающих различные переменные невозможно. Показателем, на основании которых возможно сопоставление различных уравнений является коэффициент детерминации, он обозначается :

, где — среднеарифметическое значение у.

принимает значения в интервале [0;1], чем ближе к 1, тем лучше качество подгонки регрессионного уравнения. На практике помимо коэффициента детерминации часто используются коэффициенты корреляции, показывающих степень связи между двумя переменными.

Этот показатель также независим от единиц измерения и характеризует силу и направление линейной связи между двумя переменными.

Значение коэффициента находится в интервале от (-1;1).

Если коэффициент близок к -1, то говорят об отрицательной линейной связи. Когда показатель близок к 0, то говорят о линейной независимости двух переменных. Когда показатель близок к 1 – о положительной линейной связи. При анализе коэффициентов корреляции необходимо учитывать, что коэффициент корреляции показывает только силу линейной связи.

— среднеарифметическое значение x.

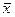
3.2. Приведенные ранее показатели качества подгонки не позволяют принять статистического решения по пригодности регрессионного уравнения, хотя и дают некоторое представление о качестве подгонки. Такие решения принимают на основе статистических критериев. Одним из таких критериев является F- критерий. Принятие решения на основе F-критерия опирается на общую процедуру проверки гипотезы. После оценки свободного члена регрессии и коэффициента регрессии выдвигается гипотеза о том, что линейная связь между x и y не подтверждается. 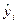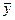Отсутствие связи можно изучить на основе отклонений расчетных значений от среднеарифметического значения .

Близкое к 0 значение свидетельствует об отсутствии какой-либо тенденции для y_i в связи с изменениями x. Строгое решение об опровержении линейной связи проверяется на основе F-статистики. Если F таб расч , то гипотезу об отсутствии линейной связи отвергаем с вероятностью p.

Значения F таб , берутся из таблицы критических точек распределения F (Фишера-Снедекора) для степеней свободы n₁=1, n₂=n-2.

Отдельно исследуется коэффициент регрессии b. Выдвигается гипотеза о том, что x влияет на y несущественно, то есть y изменяется по каким-то другим причинам, а не в связи с изменением x. Выдвинутая гипотеза равноценна тому, что b равен 0 для генеральной совокупности. Если наша гипотеза верна, то t-статистика подчиняется t-распределению со степенями свободы n-2.

, где — стандартная ошибка коэффициента b рассчитывается по формуле:

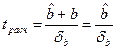
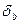
Если t расч >t табл , то с заданной вероятностью гипотезу о том, что b=0 отвергаем. t табл находится по таблице критических точек распределения Стьюдента с заданной вероятностью p b степенью свободы n-2. t-статистика используется также при построении доверительного интервала для коэффициента b.

Видео:Простые показатели качества модели регрессии (R2, критерии Акаике и Шварца)Скачать

показатели качества регрессии.

Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.

Для оценки качества модели регрессии используются специальные показатели.

Качество линейной модели парной регрессии характеризуется с помощью следующих показателей:

1) парной линейный коэффициент корреляции, который рассчитывается по формуле:

где G(x) – среднеквадратическое отклонение независимой переменной;

G(y) – среднеквадратическое отклонение зависимой переменной.

Также парный линейный коэффициент корреляции можно рассчитать через МНК-оценку коэффициента модели регрессии

Парный линейный коэффициент корреляции характеризует степень тесноты связи между исследуемыми переменными. Он рассчитывается только для количественных переменных. Чем ближе модуль значения коэффициента корреляции к единице, тем более тесной является связь между исследуемыми переменными. Данный коэффициент изменяется в пределах [-1; +1]. Если значение коэффициента корреляции находится в пределах от нуля до единицы, то связь между переменными прямая, т. е. с увеличением независимой переменной увеличивается и зависимая переменная, и наборот. Если коэффициент корреляции находится в пределах отминусеиницы до нуля, то связь между переменными обратная, т. е. с увеличением независимой переменной уменьшается зависимая переменная, и наоборот. Если коэффициент корреляции равен нулю, то связь между переменными отсутствует. Если коэффициент корреляции равен единице или минус единице, то связь между переменными существует функциональная связь, т. е. изменения независимой и зависимой переменных полностью соответствуют друг другу.

2) коэффициент детерминации рассчитывается как вадрат парного линейного коэффициента корреляции и обозначается как ryx2. Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимой переменной, в общем объёме вариации.

Качество линейной модели множественной регрессии характеризуется с помощью показателей, построенных на основе теоремы о разложении дисперсий.

Теорема. Общая дисперсия зависимой переменной может быть разложена на объяснённую и необъяснённую построенной моделью регрессии дисперсии:

где G2(y) – это общая дисперсия зависимой переменной;

σ2(y) – это объяснённая с помощью построенной модели регрессии дисперсия переменной у, которая рассчитывается по формуле:

δ2(y) – необъяснённая или остаточная дисперсия переменной у, которая рассчитывается по формуле:

С использованием теоремы о разложении дисперсий рассчитываются следующие показатели качества линейной модели множественной регрессии:

1) множественный коэффициент корреляции между зависимой переменной у и несколькими независимыми переменными хi:

Данный коэффициент характеризует степень тесноты связи между зависимой и независимыми переменными. Свойства множественного коэффициента корреляции аналогичны свойствам линейнойго парного коэффициента корреляции.

2) теоретический коэффициент детерминации рассчитывается как квадрат множественного коэффициента корреляции:

Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимых переменных;

характеризует в процентном отношении ту долю вариации зависимой переменной, которая не учитывается а построенной модели регрессии;

4) среднеквадратическая ошибка модели регрессии (Meansquareerror – MSE):

где h– это количество параметров, входящих в модель регрессии.

Если показатель среднеквадратической ошибки окажется меньше показателя среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений β(у), то модель регрессии можно считать качественной.

Показатель среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений рассчитывается по формуле:

5) показатель средней ошибки аппроксимации рассчитывается по формуле:

Если величина данного показателя составляет менее 6-7%, то качество построенной модели регрессии считается хорошим. Максимально допустимым значением показателя средней ошибки аппроксимации считается 12-15 %.

13 .

Свойства дисперсии определяются свойствами МО. Напомним, дисперсия является центральным моментом второго порядка:

Дисперсия любой случайной величины независимо от вида распределения, которому она подчиняется обладает следующими свойствами.

1.ДИСПЕРСИЯ НЕСЛУЧАЙНОЙ ВЕЛИЧИНЫ РАВНО НУЛЮ.

Пусть а — неслучайная величина. Тогда D(a)=M[(a-M(a))2]=M[0]=0.

2. ДИСПЕРСИЯ СУММЫ НЕСЛУЧАЙНОЙ И СЛУЧАЙНОЙ ВЕЛИЧИН РАВНА ДИСПЕРСИИ СЛУЧАЙНОЙ ВЕЛИЧИНЫ (ДИСПЕРСИЯ ИНВАРИАНТНА СДВИГУ).

Пусть а — неслучайная величина. Тогда D(a+x)=M[(a+x-M(a+x))2]= M[(x-M(x))2]=D(x).

3.ДИСПЕРСИЯ ПРОИЗВЕДЕНИЯ НЕСЛУЧАЙНОЙ ВЕЛИЧИНЫ НА СЛУЧАЙНУЮ РАВНА ПРОИЗВЕДЕНИЮ СЛУЧАЙНОЙ ВЕЛИЧИНЫ НА КВАДРАТ НЕСЛУЧАЙНОЙ ВЕЛИЧИНЫ.

Пусть а — неслучайная величина. Тогда D(a*x)=M[(a*x-M(a*x))2]=M[(a*(x-M(x))2]=

4. ДИСПЕРСИЯ СУММЫ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН РАВНА СУММЕ ДИСПЕРСИЙ ЭТИХ ВЕЛИЧИН И УДВОЕННОЙ КОВАРИАЦИИ ЭТИХ ВЕЛИЧИН.

Пусть x и у — случайные величины. Тогда D(x+y)=M[((x+y)-M(x+y))2]= =M[((x-Mx)+(y-My))2]=M[(x-Mx)2+(y-My)2+2*(x-Mx)*(y-My)]=M[(x-Mx)2]+ +M[(y-My)]+2*M[(x-Mx)*(y-My)]=D(x)+D(y)+2*COV(x,y).

Величина COV(x,y)=M[(x-Mx)*(y-My)] называется ковариацией и обладает свойством: ДЛЯ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН КОВАРИАЦИЯ ВСЕГДА РАВНА НУЛЮ. Отсюда, следует: ДИСПЕРСИЯ СУММЫ ДВУХ НЕЗАВИСИМЫХ (И ТОЛЬКО НЕЗАВИСИМЫХ) СЛУЧАЙНЫХ ВЕЛИЧИН РАВНА СУММЕ ДИСПЕРСИЙ ЭТИХ ВЕЛИЧИН.

Для оценки параметров нелинейных моделей используются два подхода. Первый подход основан на линеаризации модели и заключается в том, что с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными. Второй подход обычно применяется в случае, когда подобрать соответствующее линеаризующее преобразование не удается. В этом случае применяются методы нелинейной оптимизации на основе исходных переменных. Таким образом, функции, которые показывают изменение одной переменной от другой в процентах или в несколько раз являются функциями, отражающими эластичность.

10.

Обобщенный метод наименьших квадратов, теорема Айткена

Применение обычного метода наименьших квадратов при нарушении условия гомоскедастичности приводит к следующим отрицательным последствиям:

1. оценки неизвестных коэффициентов β неэффективны, то есть существуют другие оценки, которые являются несмещенными и имеют меньшую дисперсию.

2. стандартные ошибки коэффициентов регрессии будут занижены, а, следовательно, t -статистики – завышены, и будет получено неправильное представление о точности уравнения регрессии.

Обобщенный метод наименьших квадратов

Рассмотрим метод оценивания при нарушении условия гомоскедастичности, матрица имеет вид β= (ХТ Ω-1 Х)-1 ХТ Ω-1у

Расчёт неизвестных коэффициентов регрессии по данной формуле называют обобщённым методом наименьших квадратов (ОМНК).

Теорема Айткена: при нарушении предположения гомоскедастичности оценки, полученные обобщенным методом наименьших квадратов, являются несмещенными и наиболее эффективными (имеющими наименьшую вариацию). На практике матрица Ω практически никогда не известна. Поэтому часто пытаются каким-либо методом оценить оценки матрицы Ω и использовать их для оценивания. Этот метод носит название доступного обобщенного метода наименьших квадратов.

Видео:Эконометрика. Линейная парная регрессияСкачать

13.5. Качество подгонки

Один из возможных подходов основывается па том факте, что для стандартной линейной модели регрессии коэффициент детерминации Я2 совпадает с квадратом выборочного коэффициента корреляции между у и прогнозным значением у (см. упражнение 2.7)7. Исходя из этого можно для внутригрупповой регрессии (т. е. для модели с фиксированным эффектом) определить коэффициент детерминации равенством

Within = г2Ы — Уі, Уи — ft), (13.29)

Уг = (Хц — Xi)'(3pЕ И Г2(-, •) — выборочный КОэффиЦиеН’1′ корреляции (в данном случае объем выборки равен пТ).

Аналогично можно определить коэффициент детерминации для межгрупповой регрессии:

где уі = Ж-/Зв (в данном случае объем выборки равен п).

Наконец, для обычной модели объединенный коэффициент детерминации есть

^overall =r2(yit,yit), (13.31)

где уи = x’itpQ]jS.

На самом деле формулами (13.29), (13.30), (13.31) можно определить внутригрупповой, межгрупповой и объединенный коэффициенты детерминации для любой оценки /3 вектора параметров /3. При этом, естественно, считают, что уц = x’itf3, ft = Т ТЇ=і Мі. У = пТ ТІ=і Хл=і Уи- Именно такой подход реализован, например, в широко используемом эконометрическом пакете STATA: при оценивании моделей с панельными данными вычисляются три коэффициента детерминации в соответствии с формулами (13.29), (13.30), (13.31) независимо от того, какой метод оценивания применяется.

Следует сказать, что коэффициенты детерминации в моделях с панельными данными нецелесообразно использовать для того, чтобы определить, какой метод оценивания лучше. Так, если одну и ту же модель оценить, например, обычным методом наименьших квадратов и с помощью случайного эффекта, то объединенный коэффициент детерминации в первом случае всегда будет больше соответствующего объединенного коэффициента для второго метода, даже если более адекватным является использование случайного эффекта. Тем не менее коэффициенты детерминации можно применять для сравнения моделей, отличающихся набором регрессоров и оцениваемых одним и тем же методом.