Показатель пуассона в уравнении адиабатного процесса зависит от числа степеней свободы молекул газа

При изучении поведения газов в физике много внимания уделяется изопроцессам, то есть таким переходам между состояниями системы, во время которых сохраняется один термодинамический параметр. Тем не менее, существует газовый переход между состояниями, который не является изопроцессом, но который играет важную роль в природе и технике. Речь идет об адиабатическом процессе. В данной статье рассмотрим его подробнее, акцентируя внимание на том, что такое показатель адиабаты газа.

Видео:Адиабатный процесс. 10 класс.Скачать

Адиабатический процесс

Согласно термодинамическому определению, под адиабатическим процессом понимают такой переход между начальным и конечным состояниями системы, в результате которого не существует обмена теплом между внешней средой и изучаемой системой. Такой процесс возможен при наличии следующих двух условий:

• теплопроводность между внешней средой и системой по той или иной причине является низкой;
• скорость процесса велика, поэтому обмен теплом не успевает происходить.

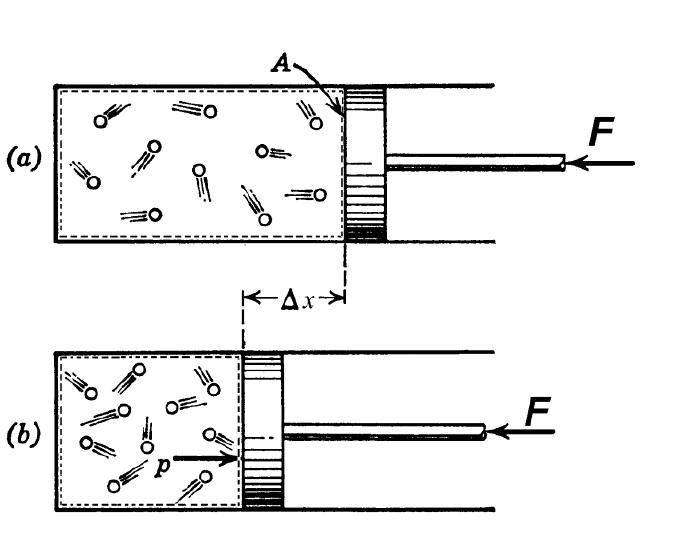
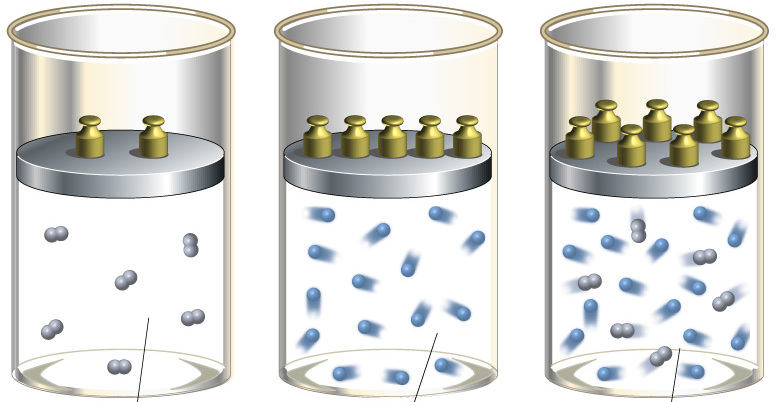
В технике адиабатный переход используют как для разогрева газа при его резком сжатии, так и для его охлаждения во время быстрого расширения. В природе рассматриваемый термодинамический переход проявляет себя, когда воздушная масса поднимается или опускается по склону холма. Такие подъемы и спуски приводят к изменению точки росы в воздухе и к возникновению осадков.

Видео:Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Уравнение Пуассона для адиабаты идеального газа

Идеальный газ представляет собой систему, в которой частицы движутся хаотично с большими скоростями, не взаимодействуют друг с другом и являются безразмерными. Такая модель является очень простой с точки зрения ее математического описания.

Согласно определению адиабатного процесса, можно записать следующее выражение в соответствии с первым законом термодинамики:

Иными словами, газ, расширяясь или сжимаясь, совершает работу P*dV за счет соответствующего изменения своей внутренней энергии dU.

В случае идеального газа, если воспользоваться уравнением его состояния (закон Клапейрона-Менделеева), то можно получить следующее выражение:

Это равенство называется уравнением Пуассона. Люди, которые знакомы с физикой газов, заметят, что если величина γ будет равна 1, то уравнение Пуассона перейдет в закон Бойля-Мариотта (изотермический процесс). Однако такое преобразование уравнений невозможно, поскольку γ для любого типа идеального газа больше единицы. Величина γ (гамма) называется показателем адиабаты идеального газа. Рассмотрим подробнее его физический смысл.

Видео:29. Адиабатический процесс. Уравнение ПуассонаСкачать

Что такое показатель адиабаты?

Показатель γ, который появляется в уравнении Пуассона для газа идеального, представляет собой отношение теплоемкости при постоянном давлении к аналогичной величине, но уже при постоянном объеме. В физике теплоемкостью называют величину теплоты, которую нужно передать данной системе или забрать у нее, чтобы она изменила свою температуру на 1 Кельвин. Будем обозначать символом C_P изобарную теплоемкость, а символом C_V — изохорную. Тогда для γ справедливо равенство:

Поскольку γ всегда больше одного, то он показывает, во сколько раз изобарная теплоемкость изучаемой газовой системы превышает аналогичную изохорную характеристику.

Видео:Физика 10 класс. Адиабатный процесс.Скачать

Теплоемкости CP и CV

Чтобы определить показатель адиабаты, следует хорошо понимать смысл величин C_P и C_V. Для этого проведем следующий мысленный эксперимент: представим, что газ находится в закрытой системе в сосуде с твердыми стенками. Если нагревать сосуд, то все сообщенное тепло в идеальном случае перейдет во внутреннюю энергию газа. В такой ситуации будет справедливо равенство:

Величина C_V определяет количество теплоты, которое следует передать системе, чтобы изохорно нагреть ее на 1 К.

Теперь предположим, что газ находится в сосуде с подвижным поршнем. В процессе нагрева такой системы поршень будет перемещаться, обеспечивая поддержание постоянного давления. Поскольку энтальпия системы в таком случае будет равна произведению изобарной теплоемкости на изменение температуры, то первый закон термодинамики примет вид:

Отсюда видно, что C_P>C_V, так как в случае изобарного изменения состояний необходимо расходовать тепло не только на повышение температуры системы, а значит, и ее внутренней энергии, но и на выполнение газом работы при его расширении.

Видео:О.Я. Савченко 5.6.28* | Вывод уравнения политропыСкачать

Величина γ для газа идеального одноатомного

Самой простой газовой системой является одноатомный идеальный газ. Предположим, что мы имеет 1 моль такого газа. Напомним, что в процессе изобарного нагрева 1 моль газа всего на 1 Кельвин, он совершает работу, равную величине R. Этим символом принято обозначать универсальную газовую постоянную. Она равна 8,314 Дж/(моль*К). Применяя последнее выражение в предыдущем пункте для данного случая, получаем такое равенство:

Откуда можно определить значение изохорной теплоемкости C_V:

Известно, что для одного моль одноатомного газа значение изохорной теплоемкости составляет:

Из последних двух равенств следует значение показателя адиабаты:

Отметим, что величина γ зависит исключительно от внутренних свойств самого газа (от многоатомности его молекул) и не зависит от количества вещества в системе.

Видео:Физика. Термодинамика: Адиабатный процесс. Центр онлайн-обучения «Фоксфорд»Скачать

Зависимость γ от числа степеней свободы

Выше было записано уравнение для изохорной теплоемкости одноатомного газа. Появившийся в нем коэффициент 3/2 связан с количеством степеней свободы у одного атома. У него существует возможность двигаться только в одном из трех направлений пространства, то есть существуют только поступательные степени свободы.

Если система образована двухатомными молекулами, то к трем поступательным добавляются еще две вращательные степени. Поэтому выражение для C_V приобретает вид:

Тогда значение γ будет равно:

Отметим, что на самом деле существует у двухатомной молекулы еще одна колебательная степень свободы, но при температурах в несколько сотен Кельвин она не задействуется и не вносит вклад в теплоемкость.

Если молекулы газа состоят из более, чем двух атомов, тогда у них будет 6 степеней свободы. Показатель адиабаты при этом будет равен:

Таким образом, при увеличении числа атомов в молекуле газа величина γ уменьшается. Если построить график адиабаты в осях P-V, то можно заметить, что кривая для одноатомного газа будет вести себя более резко, чем для многоатомного.

Видео:Основы теплотехники. Термодинамические процессы. Изохорный, изобарный, изотермический, адиабатный.Скачать

Показатель адиабаты для смеси газов

Выше мы показали, что величина γ от химического состава газовой системы не зависит. Однако она зависит от количества атомов, которое составляет ее молекулы. Предположим, что система состоит из N компонент. Атомная доля компонента i в смеси равна a_i. Тогда для определения показателя адиабаты смеси можно использовать следующее выражение:

Где γ_i — это величина γ для i-го компонента.

Например, это выражение можно применить для определения γ воздуха. Поскольку он состоит на 99 % из двухатомных молекул кислорода и азота, то его показатель адиабаты должен быть очень близок к значению 1,4, что подтверждается при экспериментальном определении этой величины.

Видео:Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Краткая теория. Отношение удельной теплоемкости при постоянном давлении сp к удельной теплоемкости при постоянном объеме сv

Отношение удельной теплоемкости при постоянном давлении с_p к удельной теплоемкости при постоянном объеме с_v, называемое показателем адиабаты

, играет в термодинамике весьма важную роль. В теории идеальных газов оно определяет число степеней свободы молекул. Это отношение входит в уравнение Пуассона, которое описывает адиабатный процесс. Этим отношением определяется скорость распространения звука в газах, от него зависит течение газов по трубам со сверхзвуковыми скоростями и другие процессы. Роль отношения заключается еще и в том, что, зная его, можно не прибегать к измерениям с_v, которые всегда трудны. Значение с_V можно получить из измеренных значений с_p и γ.

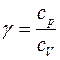
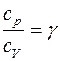
Адиабатным процессом называется процесс, осуществляющийся без теплообмена с внешней средой. Он протекает в системе, окруженной теплоизолирующей оболочкой, но его можно реализовать и при отсутствии такой оболочки. Для этого процесс должен протекать настолько быстро, чтобы за время его осуществления не произошло теплообмена между системой и окружающей средой. В настоящей лабораторной работе адиабатным можно считать быстропротекающий процесс расширения воздуха при открытом кране баллона.

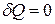
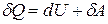
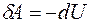
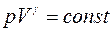
В случае адиабатного процесса и первое начало термодина­мики примет вид , т.е. при адиабат­ном процессе расширения газом совершается работа только за счет изменения запаса внутренней энергии. Этот процесс описы­вается уравнением Пуассона

, (1)

где р — давление; V — объём газа; γ — показатель адиабаты, равный отношению удельных теплоемкостей газа с_p и с_v или молярных теплоемкостей С_p и С_v:

. (2)

Выражение для γ в (2) следует из связи

, (3)

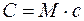
где М — молярная масса газа.

Удельной теплоемкостью с вещества называется физическая величина, численно равная количеству теплоты Q, необходимой для нагревания единицы массы вещества на один кельвин:

, , (4)

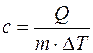
где m — масса вещества; DT = Т₂ — Т₁ — изменение температуры при нагревании вещества от температуры Т₁ до Т₂.

Молярной теплоемкостью С вещества называется физическая величина, численно равная количеству теплоты Q, необходимой для нагревания одного моля вещества на один кельвин:

, , (5)

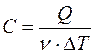
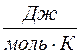
где ν – число молей вещества.

Для ве­щества в газообразном состоянии величина удельной и моляр­ной теплоёмкостей газа существенно зависит от того, при каких ус­ловиях он нагревается: при постоянном объёме или при постоян­ном давлении. В первом случае сообщенное газу тепло идёт только на уве­личение внутренней энергии газа, так как объём газа не изменяет­ся и поэтому не совершается работа расширения. Во втором слу­чае требуется дополнительное количество теплоты, необходимое для совершения работы расширения газа, так как неизменность давления обеспечивается увеличением объёма газа. Поэтому у газа различают две удельные и две молярные теплоёмкости: теплоём­кость при постоянном объёме и теплоемкость при постоянном давлении.

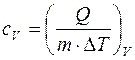
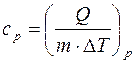
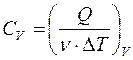
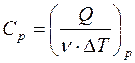
Удельной теплоемкостью с_v газа при постоян­ном объёме на­зывается физическая величина, численно равная количеству теп­лоты, необходимой для нагревания единицы массы на один кельвин при постоянном объёме: , при постоянном давлении определяется удельная теплоемкость . Молярная теплоемкость (5) при постоянном объеме равна , при постоянном давлении — .

Учитывая, что для ν молей элементарное количество теплоты δQ = νCdT,

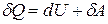
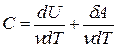
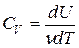
первое начало термодинамики можно записать как νСdT = dU + δA, откуда следует, что . При постоянном объеме работа газа δA = pdV= = 0 и соответствующая молярная теплоемкость равна . (6)

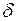
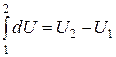
Здесь символ d употребляется для обозначения бесконечно малого приращения функции, а — для бесконечно малой величины. Бесконечно малое приращение внутренней энергии dU является полным дифференциалом, т.е. интеграл от dU зависит только от значений U в начальном и конечном состояниях: , а значит, внутренняя энергия является функцией состояния.

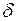
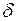
Элементарная работа А и элементарное количество теплоты Q не являются полными интегралами, поэтому работа A и количество теплоты Q являются функциями процесса.

Молярная теплоемкость при постоянном давлении равна

, (7)

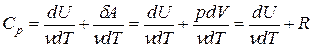
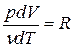
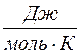
т.к. из уравнения Клапейрона-Менделеева PV = νRT следует, что , где R = = 8,314 — универсальная газовая постоянная, численно равная работе изобарного расширения одного моля газа при нагревании его на один кельвин.

Таким образом, молярная теплоемкость С_p газа при постоянном давлении больше молярной теплоёмкости C_v при постоянном объёме на универсальную газовую постоянную R:

. (8)

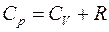
Это означает, что при изобарном процессе газу нужно сообщить кроме тепла, идущего на увеличение внутренней энергии, еще некоторое добавочное количество тепла, эквивалентное произведенной им внешней работе. Соотношение (8) называется уравнением Майера.

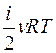
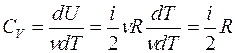
Известно, что внутренняя энергия ν молей газа определяется как U= , где i – число степеней свободы молекул газа. Числом степеней свободы называется число независимых координат, описывающих положение частицы (молекулы). Из (6) следует, что молярная теплоемкость газа при постоянном объеме равна

, (9)

а с учетом уравнения Майера (8) молярная теплоемкость при постоянном давлении равна

. (10)

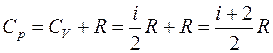
Для показателя адиабаты γ имеем

, (11)

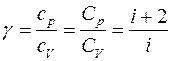
откуда видно, что величина g зависит только от числа степеней свободы молекул, из которых состоит газ.

Численное значение g различно для одно-, двух или многоатом­ных идеальных газов и зависит от числа i степеней свободы: для одноатомных i = 3, двухатомных

i = 5 и многоатомных i = 6.

Полное число степеней свободы молекулы определяется числом степеней свободы поступательного движения i_пост, вращательного движения i_вр и колебательного движения 2i_кол: i = i_пост+ i_вр+ 2i_кол . В идеальных газах не учитывается взаимодействие молекул на расстоянии, поэтому число степеней свободы колебательного движения 2i_кол (включающего равные по величине потенциальную и кинетическую энергии – отсюда множитель 2) считают равным 0.

Число поступательных степеней свободы i_пост равно 3 (в трехмерном пространстве поступательное движение центра масс молекулы можно описать тремя пространственными координатами х, у и z).

Число вращательных степеней свободы i_вр в общем случае равно трем, т.к. любое вращение сложной молекулы можно представить через сумму вращений вокруг трех осей х, у и z, проходящих через центр масс молекулы. Одноатомная молекула не вращается, двухатомная — имеет две оси вращения, как и трехатомная линейная молекула (например, углекислого газа СО₂), для них i_вр = 2, а полное число степеней свободы i = i_пост+ i_вр = 3 + 2 = 5. Для нелинейной молекулы из трех и более атомов число вращательных степеней свободы i_вр = 3, а i = i_пост+ i_вр = 3 + 3 = 6.

В атмосферном воздухе суммарные объемные доли азота N₂ (78,09 %) и кислорода О₂ (20,95 %) составляют более 99 % , поэтому воздух можно считать состоящим из двухатом­ных молекул и величину i считать приближённо рав­ной 5.

Процессы, при которых один из основных параметров состояния p, V, Т сохраняется постоянным, называются изопроцессами.

Изохорным называется процесс, протекающий при постоянном объеме V = =const, поэтому DV = dV = 0. Изохорный процесс описывается законом Гей-Люссака

const. (12)

Элементарная работа в изохорном процессе равна нулю: δA = pdV= 0, следовательно, все подводимое тепло идет на повышение внутренней энергии газа: δQ = δU.

Одним из методов определения показателя адиабаты γ для воздуха является метод Клемана и Дезорма, который также называют методом адиабатного расширения. Экспериментальная установка состоит из стеклянного баллона А (рис. 1), соединен-

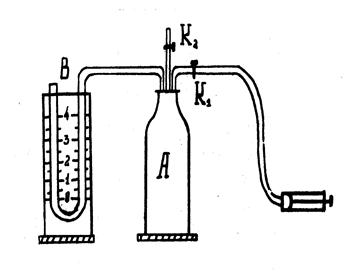Рис. 1

Н

ного с водяным манометром В и насосом Н. Водяной U-образный манометр В измеряет избыточное, по сравнению с атмосферным, давление воздуха в баллоне А. Через кран К1 воздух нагнетается в баллон, а через кран К2 — выпускается. Если кран К2 открыт, баллон сообщается с атмосферным воз­духом и давление р внутри него равно атмосферному, разность уровней воды в коленах манометра равна нулю, а температура Т в баллоне равна температуре окружающей среды.

В процессе работы воздух, заключенный в баллоне, проходит последовательно три состояния.

1. Если закрыть кран К₂ и накачать в баллон небольшое количество воз­духа, то давление в баллоне станет выше атмосферного, что отме­чается возникновением разности уровней воды в коленах манометра. При сжатии (накачке) воздух в баллоне нагревается выше комнатной температуры, после закрытия крана К₂ начинается теплообмен с внешней средой через стенки баллона. Это процесс изохорного охлаждения, который прекращается, когда воздух в баллоне примет температуру окружающей среды T₁. При этом разность уровней в манометре станет устойчивой и равной ρgh₁, где ρ – плотность воды в манометре; g— ускорение свободного падения; h₁ – разность уровней воды в коленах манометра. Состояние I воздуха в баллоне характеризуется температурой T₁, давлением р₁= р₀+ ρgh₁, где р₀ – атмосферное давление, а ρgh₁— добавочное давление, избыточное над атмосферным.

2. Если открыть и быстро закрыть кран К₂, то часть воздуха выйдет из бал­лона и давление сравняется с атмосферным р₀, а температура газа по­низится до Т₂

Видео:Лекция по физике №8. Распределение Больцмана. Теплоёмкость, Уравнение адиабатического процесса.Скачать

Экспериментальное определение постоянной адиабаты

Лабораторная работа 4

Экспериментальное определение постоянной адиабаты

Изучить закономерности адиабатного процесса. Освоить метод определения отношения удельных теплоемкостей воздуха.

Приборы и принадлежности

Закрытый стеклянный сосуд с краном. Манометр. Поршневой насос. Зажим.

Любые процессы, протекающие в газах, подчиняются первому закону (началу) термодинамики, являющемуся по — существу законом сохранения и превращения энергии:

, (1)

где – элементарное количество теплоты, получаемое газом;

– приращение внутренней энергии газа;

– элементарная работа, совершаемая газом.

Совершаемая газом работа определяется выражением:

, (2)

где p – давление газа;

dV – приращение объема, занимаемого газом.

Внутренняя энергия идеального газа — это суммарная кинетическая энергия поступательного и вращательного движения всех его молекул. Изменение внутренней энергии однозначно связано с изменением температуры:

, (3)

где м и m – соответственно молярная масса и масса вещества;

R= 8.31 — универсальная газовая постоянная;

dT – изменение температуры газа;

i – число степеней свободы молекул (число независимых координат, задающих изменение положения молекулы в пространстве при поступательном движении и вращении). Поскольку вращение атома вокруг собственной оси не изменяет его положения в пространстве, то для одноатомных молекул i = 3, для двухатомных i = 5, для трехатомных и более i = 6.

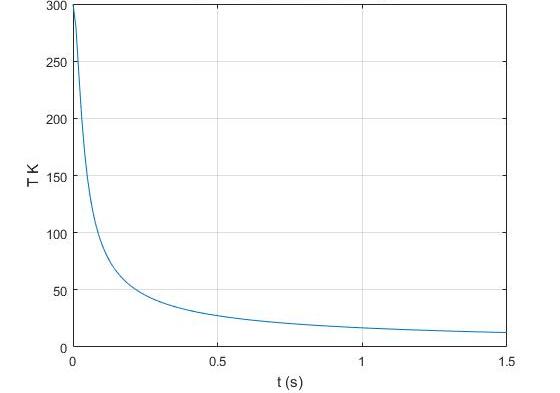
Количество теплоты получаемое (дQ > 0) или отдаваемое (дQ 0), а при быстром расширении – охлаждаются;

2) работа при адиабатном расширении газа (дA>0) совершается за счет уменьшения его внутренней энергии (dU CV, поэтому г >1.

На рисунке 1 приведен график адиабатного процесса (адиабата) и для сравнения – график изотермического процесса (изотерма). Поскольку в уравнении изотермы объем в 1-й степени, то и давление изменяется менее резко.

Как и сами теплоемкости, их отношение для чистых газов может быть рассчитано теоретически:

. (21)

В других случаях величину г определяют опытным путем.

III. Теория эксперимента

Возьмем стеклянный сосуд, оборудованный манометром и соединяющийся посредством крана с атмосферой или насосом. Пусть первоначально в сосуде было атмосферное давление Ро. Если с помощью насоса быстро накачать в сосуд некоторое количество воздуха и закрыть кран, то в результате адиабатного сжатия температура воздуха в сосуде повысится, и устойчивая разность уровней воды в манометре h1 установится тогда, когда в результате теплообмена температура воздуха в сосуде сравняется с температурой окружающей среды Т0.

Это состояние газа назовем первым и будем характеризовать давлением Р1 и температурой Т1. Из предыдущего ясно, что

Если теперь открыть кран, то воздух будет быстро выходить из сосуда, пока его давление не сравняется с атмосферным Р0 . Поскольку расширение газа можно считать адиабатным, то температура снизится до Т2. Назовем это вторым состоянием с параметрами Р2 и Т2. При этом Р2 = Р0.

Если сразу, как только давление воздуха в сосуде сравняется с атмосферным, снова закрыть кран, то давление газа в сосуде будет возрастать в результате нагрева от окружающего воздуха. Окончательная разность уровней жидкости в манометре h2 установится при температуре в сосуде, равной температуре окружающего воздуха Т0. Это будет третьим состоянием газа в сосуде:

К процессу адиабатного расширения, т. е. к переходу из состояния 1 в состояние 2, может быть применен закон Пуассона (20), который для двух состояний записывается в следующей формуле:

. (24)

Так как переход из состояния 2 в состояние 3 происходит без изменения объема (изохорический процесс), то, применяя закон Шарля, получим:

. (25)

Из уравнений (24,25) с учетом условий (22,23)получаем:

.

Так как и — величины малые по сравнению с единицей, то разлагая оба двучлена по биному Ньютона, получим в первом порядке приближения:

, откуда

и . (26)

Прибор состоит из стеклянного герметически закупоренного баллона А (рис. 2). Сквозь пробку баллона проходят три трубки. Они соединяются с водяным манометром М. Вторая – с краном К1 для быстрого выпуска и впуска воздуха. Третья подведена к насосу. Кроме того, имеется зажим К на трубе, ведущий к насосу.

Рис. 2. Прибор для определения постоянной адиабаты

Результаты измерений разностей уровней в коленах манометра

Обработка результатов измерений

Вычислить г для каждого измерения по формуле Определить среднее значение абсолютной погрешности . Подсчитать относительную погрешность:

.

Записать окончательный результат в виде:

.

Вопросы для подготовки к отчету по работе

Какой процесс называется адиабатным? Каким путем осуществляются адиабатные процессы? Запишите уравнение первого начала термодинамики для адиабатного процесса. Почему Ср больше ? Что такое внутренняя энергия газа? Изобразите графически изотермический и адиабатный процессы. Что происходит с температурой газа при адиабатном сжатии? Где на практике осуществляются адиабатные процессы? Какой процесс называется круговым? Чему равна работа при адиабатном изменении объема газа?

В каком случае и почему адиабатный процесс нужно проводить быстро? Дайте определение удельной теплоемкости при постоянном давлении. В каких единицах измеряется молярная теплоемкость при постоянном объеме? Что происходит с температурой газа при адиабатном расширении? Какой газ называют идеальным? Чему равна внутренняя энергия одного моля газа? Почему отношение теплоемкостей больше единицы? Сравните полученный Вами результат с табличным и объясните, почему они не совпадают? Как уравнение Пуассона связывает давление и объем при адиабатном процессе? Дайте описание установки для определения отношения теплоемкостей.

Можно ли считать расширение и сжатие горючей смеси в двигателях внутреннего сгорания адиабатным процессом? Пояснить. Как уравнение Пуассона связывает температуру и давление при адиабатном процессе? Как связаны между собой молярная и удельная теплоемкости при постоянном объеме? Что называется числом степеней свободы? Вычислите внутреннюю энергию 1 моля воздуха при 270 С. Вычислите теоретически отношение теплоемкостей воздуха. Запишите первое начало термодинамики для адиабатного сжатия. Вычислите молярную теплоемкость воздуха при постоянном объеме. Изобразите графически адиабатный процесс. Почему при адиабатном расширении газа его температура понижается?

🔍 Видео

9. Уравнение ПуассонаСкачать

Урок 170. Количество теплоты. Первый закон термодинамикиСкачать

Распределение Максвелла — Больцмана (часть 6) | Термодинамика | ФизикаСкачать

30. Политропические процессыСкачать

Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать

Определение показателя адиабатыСкачать

Урок 178. Тепловые двигатели и их КПД. Цикл КарноСкачать

Количество теплоты, удельная теплоемкость вещества. 8 класс.Скачать

Формула ПуассонаСкачать

Физика (лекция 22)Скачать

Изопроцессы, Адиабатный процесс.Скачать