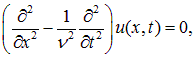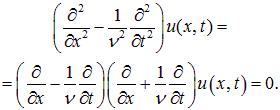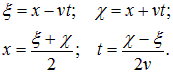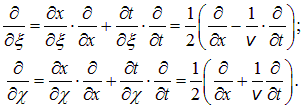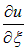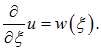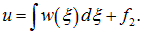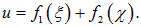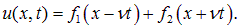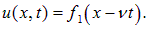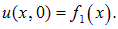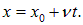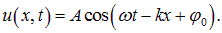Показать что любая дифференцируемая функция вида f t ax является решением волнового уравнения (6 видео)

2.2. Решение волнового уравнения

Уравнение типа (2.2), описывающее колебания различных упругих сред, называется волновым уравнением. Запишем его формально в виде:

Введем теперь вместо (x, t) новые переменные:

Производные по новым переменным выражаются по стандартным правилам дифференцирования сложной функции:

Отсюда следует, что уравнение (2.16) в новых переменных записывается в виде:

Поскольку производная по равна нулю,

не зависит от этой переменной и, следовательно, является некоторой функцией w только от переменной :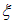

Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Интегрируем теперь это уравнение:

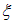
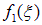
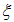
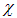
Первое слагаемое в правой части является только функцией переменной , которую мы обозначим как . Второе слагаемое — постоянная интегрирования. Она не зависит от , являясь, стало быть, функцией только переменной :

Мы получили, что решение волнового уравнения имеет вид:

Подставляя сюда выражения (2.17), мы возвращаемся к прежним переменным (x, t):

Функции f₁ и f₂ — совершенно произвольны и должны быть определены из начальных и граничных условий.

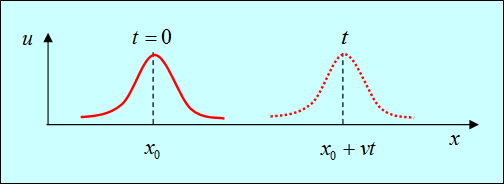
Обсудим физический смысл полученных решений. Ограничимся сначала первым слагаемым. Пусть

В момент времени t = 0 функция f₁(x) задает распределение смещений (профиль струны, деформацию твердого тела, распределение давления или частиц в газе и т. д.):

Предположим, например, что это распределение имеет максимум в точке 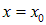(рис. 2.6).

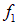
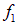
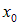
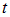
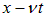
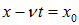
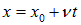
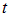
Такое распределение называют обычно волновым пакетом. В момент t максимум функции по-прежнему будет в точке, в которой аргумент равен , но теперь (в момент времени ) аргумент равен , таким образом: или . Другими словами, за время от 0 до волновой пакет сдвинется вправо на расстояние vt, так что максимум теперь придется на точку

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Нетрудно сообразить, что форму свою волновой пакет при этом перемещении не изменит.

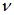
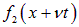
Мы видим, что начальное распределение движется вправо со скоростью . Аналогично, второе слагаемое, , описывает движение волнового пакета налево с той же скоростью . Общее решение (2.21) является суперпозицией двух этих решений.

В свою очередь, любой волновой пакет может быть представлен как суперпозиция гармонических функций. Отсюда — особая роль решений волнового уравнения вида:

Это решение описывает монохроматическую волну, распространяющуюся направо со скоростью

Решение волнового уравнения.

Известно два подхода к решению уравнения (1.61) (рис. 1.16). Первый подход состоит в непосредственном решении уравнения (1.61) и позволяет легко понять физическую картину явлений. Данный подход был предложен П. Эвальдом и М. Лауэ в 1926 г.

Второй подход сводится к преобразованию уравнения (1.61) в систему дифференциальных уравнений первого порядка в частных производных. Впервые такой подход был реализован С. Такаги (1969) и затем Д. Топеном (1967) [6, 7] и получил название уравнений Такаги—Топена. Эта система уравнений легко может быть обобщена на случай деформированного кристалла.

Видео:5. Решение волнового уравнения на отрезке методом ФурьеСкачать

Рассмотрим подход П. Эвальда и М. Лауэ к решению уравнения

(1.61) . Волновое уравнение (1.61) имеет бесчисленное множество частных решений D](r, t), D₂(r, t), . D„(r, t)- Например, для плоских волн

Здесь к — волновой вектор падающей волны в вакууме (перпендикулярен фронту волны)

Рис. 1.16. Два подхода к решению волнового уравнения:

К„ — волновой вектор л-й дифрагированной волны; л — номер дифрагированной волны; т — номер узла обратной решетки с индексами (hkl); к — волновой вектор падающей волны в вакууме х; — поляризуемость среды; D — вектор электрической индукции; /’ — мнимая единица; z,x — текущие координаты в плоскости рассеяния; С — коэффициент поляризации; а(г) — функция, описывающая локальные разориентации кристаллической решетки, связанные с дефектом; Н_ш — вектор обратной решетки; U(r) — функция поля смещений, определяемая полем дефекта

В случае распространения волны в кристалле необходимо учесть отличие коэффициента преломления от единицы. Выше отмечалось, что коэффициент преломления мало отличается от единицы, однако в динамическом приближениия при учете многократного рассеяния это может иметь существенное значение. Тогда уравнение волны следует записать как

Видео:Урок 454. Понятие о волновой функцииСкачать

Общее решение представляется суперпозицией частных решений и может быть записано в виде

Амплитуды волн Aj не зависят от времени, но могут меняться в пространстве, т.е. зависеть от координат. Дело в том, что электроны колеблются под действием распространяющейся волны, и испускаемые ими электромагнитные волны интерферируют между собой и с исходной волной. В результате устанавливается некоторое стационарное поле, характер которого определяется функцией распределения электронной плотности р(г) в кристаллической решетке. Поэтому, если мы имеем дело с кристаллической решеткой, распределение электронной плотности можно разложить в ряд Фурье по векторам обратной решетки:

Подставив выражение (1.63) в соотношение для поляризуемости среды (1.55), получим

Выражение в фигурных скобках есть не что иное, как Фурье-компо- нента разложения поляризуемости среды по векторам обратной решетки, и, следовательно, формулу (1.64) можно записать в виде

Выражение (1.66) показывает, что Xhki = Xн может иметь действительную и мнимую части, т.е. %_н = хн_г + Хн,> что соответствует учету поглощения в среде, причем в общем случае для структур, не имеющих центра симметрии, Хн ^ Хн• Численное значение действительной части X составляет величину порядка КГ 6 .

Как уже отмечалось выше, решение волнового уравнения можно представить в виде плоских волн,

где амплитуда А(г) должна иметь периодичность кристаллической решетки и может быть записана в виде ряда Фурье по векторам обратной решетки

Видео:5.1 Задача Коши для уравнений теплопроводности IСкачать

Индекс суммирования т определяет здесь узел в обратной решетке с индексами (hkl). Тогда решение волнового уравнения может быть записано в виде пакета плоских волн, или блоховской волны, с амплитудой, имеющей периодичность решетки:

Несложные, но достаточно громоздкие преобразвания приводят в конечном счете к уравнениям, связывающим волновые векторы распространяющихся в кристалле волн с их амплитудами (см. прил. 4):

Здесь (D_m)_n — проекция вектора D_m на направление, перпендикулярное вектору К„.

Полученные уравнения (1.69) называются фундаментальными уравнениями динамической теории [1, 4, 5,11]. Они представляют собой систему линейных уравнений, число которых равно числу волн с индукцией D. и связывают между собой значения волновых векторов и амплитуд волн самосогласованного волнового поля в кристаллической решетке, возбужденного внешней падающей волной. Другими словами, полученная система уравнений (1.69) связывает значения волновых векторов и энергий соответствующих мод. Таким образом, уравнения (1.69) — это дисперсионные уравнения для самосогласованного поля в кристаллической решетке.

Рис. 1.17. Геометрическая интерпретация связи волновых векторов с дисперсионной поверхностью

На рис. 1.17 приведена геометрическая интерпретация системы уравнений (1.69). Согласно представлениям Эвальда, дисперсионные уравнения описывают ш-листную поверхность, называемую дисперсионной поверхностью, в обратном пространстве в окрестности точки Лауэ (точные условия дифракции). Если из любой точки М дисперсионной поверхности (см. рис. 1.17) провести прямые линии в точки обратного пространства с индексами 0, 1, . т, полученные отрезки будут волновыми векторами Kq, К_ь . К„ волн самосогласованного волнового поля, распространяющегося в кристалле. Узлы 0, 1, 2, 3 соответствуют узлам обратной решетки с индексами h₀k₀l₀, hfali h₂k₂l2,h₃k₃l2, одновременно участвующими в дифракции. Таким образом, поверхность, описываемая дисперсионными уравнениями, является геометрическим местом точек распространения для m-волновой дифракционной задачи.