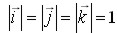Прямолинейное равномерное движение– движение, при котором материальная точка (тело) за любые равные промежутки времени совершает одинаковые перемещения.
Скорость равномерного прямолинейного движения– векторная физическая величина, равная отношению перемещения материальной точки (тела) за любой промежуток времени к значению этого промежутка ( 
).
Единица скорости в СИ – 1 м/с.
Средняя путевая скорость – скалярная физическая величина, равная отношению пути, пройденного точкой (телом) за некоторый отрезок времени, к величине этого отрезка времени ( 
= 
).
Средняя скорость перемещения – векторная физическая величина, равная отношению перемещения точки (тела) за некоторый отрезок времени к величине этого отрезка времени ( 
)
Кинематические уравнения равномерного прямолинейного движения (векторная и скалярная форма):
Равнопеременное прямолинейное движение. Средняя и мгновенная скорости. Ускорение, единица ускорения в СИ. Кинематические уравнения равнопеременного прямолинейного движения (векторная и скалярная форма)
Прямолинейное равнопеременное (равноускоренное) движение– движение,при котором скорость материальной точки (тела) за любые одинаковые промежутки времени изменяется одинаково.
Средняя скорость равнопеременного движения – отношение всего пути, пройденного точкой, ко всему времени движения ( = S/t).
Мгновенная скорость – скорость точки (тела) в данный момент времени или в данной точке траектории.
Ускорение – векторная физическая величина, равная отношению изменения скорости точки (тела) к отрезку времени, в течение которого это изменение произошло ( 
).
Единица ускорения в СИ – 1 м/с 
.
Кинематические уравнения равнопеременного прямолинейного движения (векторная и скалярная форма):
; 
; 
Видео:Физика - уравнения равноускоренного движенияСкачать
Кинематика Основные понятия, законы и формулы
Основные понятия, законы и формулы.
Кинематика — раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих движение.
Механическим движением называют изменение положения тела в пространстве с течением времени относительно других тел.
Простейшим механическим движением является движение материальной точки — тела, размеры и форму которого можно не учитывать при описании его движения.
Движение материальной точки характеризуют траекторией, длиной пути, перемещением, скоростью и ускорением.
Траекторией называют линию в пространстве, описываемую точкой при своем движении.
Расстояние, пройденное телом вдоль траектории движения, — путь(S).
Перемещение 
— направленный отрезок, соединяющий начальное и конечное положение тела.
Длина пути — величина скалярная, перемещение — величина векторная.
Средняя скорость 
— это физическая величена, равная отношению вектора перемещения к промежутку времени, за которое произошло перемещение:
.
Мгновенная скорость или скорость в данной точке траектории 
— это физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Dt:
.
Величину характеризующую изменение скорости за единицу времени, называют средним ускорением 
:
.
Аналогично понятию мгновенной скорости вводится понятие мгновенного ускорения
:
.
При равноускоренном движении ускорение постоянно.
Простейший вид механического движения-прямолинейное движение точки с постоянным ускорением.
Движение с постоянным ускорением 
называется равнопеременным; в этом случае:
; 
; 
.
Частным случаем прямолинейного движения с постоянным ускорением является падение тел с небольшой высоты (много меньшей радиуса Земли).
; 
; 
.
Простейшим видом криволинейного движения является равномерное движение точки по окружности:
; 
;
где 
и 
.
Связь между линейными и угловыми величинами при вращательном движении:
; 
; 
; 
.
Любое сложное движение можно рассматривать как результат сложения простых движений. Результирующее перемещение равно геометрической сумме и находится по правилу сложения векторов. Скорость тела и скорость системы отсчета так же складывается векторно.
, 
.
При решении задач на те или иные разделы курса, кроме общих правил решения, приходится учитывать некоторые дополнения к ним, связанные со спецификой самих разделов.
Задачи по кинематике, разбираемые в курсе элементарной физики, включают в себя: задачи о равнопеременном прямолинейном движении одной или нескольких точек, задачи о криволинейном движении точки на плоскости. Мы рассмотрим каждый из этих типов задач отдельно.
Прочитав условие задачи, нужно сделать схематический чертеж, на котором следует изобразить систему отсчета, и указать траекторию движения точки.
После того как выполнен чертеж, с помощью формул:
; ; .
устанавливают связь между величинами, отмеченными на чертеже.
Cоставив полную систему кинематических уравнений, описывающих движение точки, нужно записать в виде вспомогательных уравнений все дополнительные условия задачи.
Проверив число неизвестных в полученной системе уравнений, можно приступать к ее решению относительно искомых величин.
Решение задач о движении одних тел относительно других, которые в свою очередь двигаются относительно тела, принятого за неподвижное (чаще всего его связывают с Землей), начинают с выбора системы отсчета.
Для этого необходимо тщательно продумать условие задачи и выяснить, к какой системе относятся заданные и искомые характеристики движения.
Затем нужно установить подвижную и неподвижную системы отсчета, для движущихся тел указать кинематические характеристики относительного и переносного движений и составить уравнения движения отдельно для подвижной и неподвижной систем отсчета.
Составляя эти уравнения, необходимо следить за тем, чтобы начало отсчета времени было одинаковым для всех движущихся тел. Связь между абсолютным, переносным и относительным движениями задается формулами:
; .
Подстановкой в них развёрнутых выражений для Sn, S0, vn, v0 и т. д. и заканчивается первая часть решения.
Пример 1. Велосипедист ехал из одного города в другой. Половину пути он проехал со скоростью v1 = 12 км/ч далее половину оставшегося времени он ехал со скоростью v2 = 6 км/ч, а затем до конца пути шел пешком со скоростью v3 = 4 км/ч. Определить среднюю скорость велосипедиста на всем пути.
а) Эта задача на равномерное прямолинейное движение одного тела. Представляем ввиде схемы. При составлении ее изображаем траекторию движения и выбираем на ней начало отсчета (точка 0). Весь путь разбиваем на три отрезка S1,S2, S3, на каждом из них указываем скорости v1, v2, v3 и отмечаем время движения t1, t2, t3.
S = S1 + S2 + S3, t = t1 + t2 + t3.
б) Составляем уравнения движения для каждого отрезка пути:
S1 = v1t1; S2 = v2t2; S3 = v3t3 и записываем дополнительные условия задачи:
S1 = S2 + S3; t2 = t3; 
.
в) Читаем еще раз условие задачи, выписываем числовые значения известных величин и, определив число неизвестных в полученной системе уравнений (их 7: S1, S2, S3, t1, t2, t3, vср), решаем ее относительно искомой величины vср.
Если при решении задачи полностью учтены все условия, но в составленных уравнениях число неизвестных получается больше числа уравнений, это означает, что при последующих вычислениях одно из неизвестных сократится, такой случай имеет место и в данной задаче.
Решение системы относительно средней скорости дает:
.
г) Подставив числовые значения в расчётную формулу, получим:
; vср 7 км/ч.
Напоминаем, что числовые значения удобнее подставлять в окончательную расчетную формулу, минуя все промежуточные. Это экономит время на решение задачи и предотвращает дополнительные ошибки в расчётах.
Решая задачи на движение тел, брошенных вертикально вверх, нужно обратить особое внимание на следующее. Уравнения скорости и перемещения для тела, брошенного вертикально вверх, дают общую зависимость v и h от t для всего времени движения тела. Они справедливы (со знаком минус) не только для замедленного подъема вверх, но и для дальнейшего равноускоренного падения тела, поскольку движение тела после мгновенной остановки в верхней точке траектории происходит с прежним ускоронием. Под h при этом всегда подразумевают перемещение движущейся точки по вертикали, то есть ее координату в данный момент времени — расстояние от начала отсчета движения до точки.
Если тело брошено вертикально вверх со скоростью V0, то время tпод и высота hmax его подъема равны :
; 
.
Кроме того, время падения этого тела в исходную точку равно времени подъема на максимальную высоту (tпад = tпод), а скорость падения равна начальной скорости бросания (vпад = v0).
Пример 2. Тело брошено вертикально вверх с начальной скоростью v0 = 3,13 м/с. Когда оно достигло верхней точки полета, из того же начального пункта с такой же начальной скоростью бросили второе тело. Определите, на каком расстоянии от точки бросания встретятся тела; сопротивление воздуха не учитывать.
Решение. Делаем чертеж. Отмечаем на нем траекторию движения первого и второго тела. Выбрав начало отсчета в точке, указываем начальную скорость тел v0, высоту h, на которой произошла встреча (координату y=h), и время t1 и t2 движения каждого тела до момента встречи.
Уравнение перемещения тела, брошенного вверх, позволяет найти координату движущегося тела для любого момента времени независимо от того, поднимается ли тело вверх или падает после подъема вниз, поэтому для первого тела
,
.
Третье уравнение составляем, исходя из условия, что второе тело бросили позднее первого на время максимального подъема:
.
Решая систему трех уравнений относительно h, получаем:
; 
; 
.
б) В задачах на криволинейное движение точки можно выделить задачи о движении точки по окружности и задачи о движении тел, брошенных под углом к горизонту.
Решение задач о движении точки по окружности принципиально ничем не отличается от решения задач о прямолинейном движении. Особенность состоит лишь в том, что здесь наряду с общими формулами кинематики приходится учитывать связь между угловыми и линейными характеристиками движения.
; 
,
где и ; ; 
; 
.
Движение тел, брошенных под углом к горизонту, можно рассматривать как результат наложения двух одновременных прямолинейных движений по осям OX и ОУ, направленных вдоль поверхности Земли и по нормали к ней. Учитывая это, решение всех задач такого типа удобно начинать с разложения вектора скорости и ускорения по указанным осям и затем составлять кинематические уравнения движения для каждого направления. Необходимо при этом иметь ввиду, что тело, брошенное под углом к горизонту, при отсутствии сопротивления воздуха и небольшой начальной скорости летит по параболе, и время движения по оси ОХ равно времени движения по оси ОУ, поскольку оба эти движения происходят одновременно.
Пример 3. Артиллерийское орудие расположено на горе высотой h. Снаряд вылетает из ствола со скоростью v0, направленной под углом a к горизонту. Пренебрегая сопротивлением воздуха, определите:
а) дальность полета снаряда по горизонтальному направлению ;
б) скорость снаряда в момент падения ;
г)начальный угол стрельбы, при котором дальность полета наибольшая.
Прямоугольную систему координат выбираем так, чтобы ее начало совпало с точкой бросания, а оси были направлены вдоль поверхности Земли и по нормали к ней в сторону начального смещения снаряда. Изображаем траекторию снаряда, его начальную скорость 
, угол бросания a, высоту h, горизонтальное перемещение S, скорость в момент падения (она направлена по касательной к траектории в точке падения) и угол падения j (углом падения тела называют угол между касательной к траектории, проведенной в точку падения, и нормалью к поверхности Земли).
Движение тела, брошенного под углом к горизонту, можно представить как результат сложения двух прямолинейных движений: одного-вдоль поверхности Земли (оно будет равномерным, поскольку сопротивление воздуха не учитывается) и второго-перпендикулярно поверхности Земли (в данном случае это будет движение тела, брошенного вертикально вверх). Для замены сложного движения двумя простыми разложим (по правилу параллелограмма) скорости и 
на горизонтальные и вертикальные составляющие и найдем их проекций 
и 
— для скорости и vx и vy — для скорости .
а, б) Составляем уравнение скорости и перемещения для их проекций по каждому направлению. Так как в горизонтальном направлении снаряд летит равномерно, то его скорость и координаты в любой момент времени удовлетворяют уравнениям
(1)
и 
. (2)
Для вертикального направления:
(3)
и 
. (4)
В момент времени t1, когда снаряд упадет на землю, его координаты равны:
(5)
В последнем уравнении перемещение h взято со знаком «минус», так как за время движения снаряд сместится относительно уровня отсчета 0 высоты в сторону противоположную направлению, принятому за положительное.
Результирующая скорость в момент падения равна :
. (6)
В составленной системе уравнений пять неизвестных, нам нужно определить S и v.
Из уравнений (4) и (5) находим время полета снаряда :
.
Подставляя выражения для t1 формулы (2) и (3) с учетом (5), соответственно получаем:
; (7)
. (8)
После этого из (6) с учетом (1) и (8) находим:
. (9)
Из полученных результатов можно сделать следующие выводы.
Если h = 0, то есть снаряды падают на уровне вылета, то согласно формуле (7) дальность их полета будет равна :
.
Если при этом угол бросания равен 45град (sin 2a = 1), то при заданной начальной скорости v0 дальность полета наибольшая:
.
Подставив в выражение (9) значение h = 0, получим, что скорость снаряда в момент его полета к уровню, с которого был произведен выстрел, равна его начальной скорости: v = v0.
При отсутствии сопротивления воздуха, скрость падения тел равна начальной скорости бросания независимо от того, под каким углом было брошено тело, лишь бы точки бросания и падения находились на одном уровне. Учитывая, что горизонтальная составляющая скорости с течением времени не изменяется, легко установить, что в момент падения скорость тела образует с горизонтом такой же угол, как и в момент бросания.
д) Решая уровнения (2), (4) и (5) относительно начального угла бросания a получим:
. (10)
Поскольку угол бросания не может быть мнимым, то это выражение имеет физический смысл лишь при условии, что
,
то есть
,
откуда следует, что максимальное перемещение снаряда по горизонтальному направлению равно:
.
Подставляя выражение для S = Smax в формулу (10), получим для угла a, при котором дальность полета наибольшая:
.
Видео:Урок 7. Механическое движение. Основные определения кинематики.Скачать
Кинематические уравнения движения
Кинематика материальной точки
Кинематика изучает движение тел, не интересуясь причинами, обусловливающими это движение.
Всякое движение относительно, так как понятие перемещение в пространстве или движение имеет строго определенное содержание только при указании, относительно каких именно тел перемещается рассматриваемый объект.
Совокупность тела или системы тел, условно принятых за неподвижные, относительно которых определяется положение остальных тел, и прибора для отсчета времени (синхронизированных часов) называется пространственно-временной системой отсчета.
Для того, чтобы иметь возможность изучать конкретные движения тел, необходимо зафиксировать некоторую точку тела, принятого условно за неподвижное, то есть выбрать так называемое начало отсчета, относительно которого и будет производиться отсчет положения движущихся тел. Далее, для определения положения данного тела относительно начала отсчета необходимо выбрать масштаб отсчета расстояний и направления отчета положения. Обычно для этого пользуются тремя взаимно перпендикулярными осями декартовых координат или так называемыми обобщенными криволинейными координатами, к числу которых относятся полярные, цилиндрические и сферические системы координат. Часто выбор системы координат определяется постановкой самой задачи. Например, при изучении движения жидкости по цилиндрической трубе наиболее удобными оказываются цилиндрические координаты, в случае исследования обтекания сферы жидкостью или газом — сферические.
Наконец, поскольку движение тел совершается с течением времени, то для его описания необходимо выбрать начало отсчета времени и масштаб времени.
Итак, элементами системы отсчета, необходимыми для описания движений, являются: начало отсчета, масштабы отсчета расстояний, три направления отсчета положения тел, начало отсчета времени, масштаб времени.
Очевидно, что одно и то же движение в различных системах отсчета, движущихся относительно друг друга, будет выглядеть по-разному. Так, скорость, ускорение, направление и траектория движения пассажира, идущего от передней к задней стенке вагона, ускоренно движущегося по криволинейному железнодорожному пути, будут различными, если это движение рассматривать в системах отсчета, связанных: а) с движущимся вагоном; б) с Землей; в) с Солнцем и т.д.
Кинематические уравнения движения
Если с выбранными телами отсчета мы связали какую-либо систему координат, то движение тела можно изучать относительно этой системы координат.
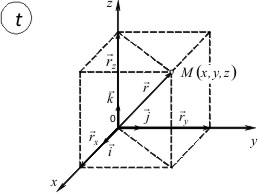
Для определения положения тела в пространстве обычно пользуются декартовой системой координат x,y,z (рис. 1.1).
Положение точки M относительно системы отсчета можно задать с помощью трех ее декартовых координат x,y,z представляющими собой расстояния от этой точки до координатных плоскостей yz, zx, xy соответственно.
Три координаты x,y,z можно объединить в один направленный отрезок или радиус-вектор r, проведенный из начала координат в рассматриваемую точку. Координаты x,y,z являются его проекциями на координатные оси, а потому
(1.1)
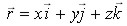
где i,j,k — координатные орты, то есть единичные векторы, направленные вдоль положительного направления координатных осей x,y,z соответственно, то есть
Геометрически вектор представляется диагональю параллелепипеда, построенного на трех взаимно перпендикулярных векторах rx=xi, ry=yj, rz=zk и по величине (по модулю) равен
(1.2)
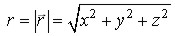
Будем пользоваться правой координатной системой, различать которую можно с помощью правила буравчика. Ввинчивая буравчик с правой нарезкой, вращая его ручку в плоскости xy кратчайшим путем от положительного конца оси x к положительному концу оси y, получим поступательное перемещение буравчика, совпадающее с положительным направлением оси z.
Движение точки будет описано полностью, если будет известно ее положение в любой момент времени относительно выбранной системы отсчета.
При движении материальной точки M ее координаты z,y,z и радиус-вектор r изменяются с течением времени t. В механике время считается аргументом, то есть независимым переменным, поэтому для задания закона движения материальной точки необходимо указать либо вид функциональной зависимости всех ее трех координат от времени
(1.3)
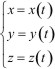
либо зависимость от времени ее радиус-вектора
Уравнения (1.3) и (1.4) называют кинематическими уравнениями движения материальной точки.
Геометрическое место точек концов радиус-вектора r называют траекторией точки M. Уравнения движения задают траекторию точки в параметрической форме. Роль параметра играет время t. Если надо получить уравнение траектории из кинематических уравнений движения исключают время, получая уравнение траектории, указывающее связь между тремя координатами любой точки.
📽️ Видео
Основные понятия и уравнения кинематики равноускоренного движения тела.Скачать
ФИЗИКА ЕГЭ 2021. Кинематика. Графики движения. Часть 1.Скачать
10 класс урок №4 Основные понятия кинематики равноускоренного движенияСкачать
Физика. 10 класс. Основные понятия и уравнения кинематики равноускоренного движения тела/07.09.2020/Скачать
Уравнение движенияСкачать
Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать
Урок 15. Решение задач на графики движенияСкачать
Задача из ЕГЭ по физике │Анализ графика #1Скачать
Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать
Кинематика. Закон движения. Урок 3Скачать
10 класс - Физика - Кинематические и динамические характеристики движенияСкачать
Физика 10 класс (Урок№2 - Равномерное прямолинейное движение материальной точки.)Скачать
Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать
Кинематика вращательного движения. ТермехСкачать
Поступательное и вращательное движенияСкачать
Уравнения и графики механических гармонических колебаний. 11 класс.Скачать
Прямолинейное движение. 10 класс.Скачать
Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать
