В ходе решения систем линейных уравнений нужно стараться использовать не «школьный метод», а метод почленного сложения (вычитания) уравнений системы. Почему? Это экономит время и упрощает вычисления, как сейчас увидите.
Пример 4:
Решить систему линейных уравнений:
Мы взяли ту же систему, что и в первом примере.
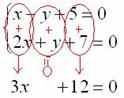
Анализируя систему уравнений, замечаем, что коэффициенты при переменной y одинаковы по модулю и противоположны по знаку (–1 и 1). В такой ситуации уравнения можно сложить почленно:
Действия, обведенные красным цветом, выполняются МЫСЛЕННО. Как видите, в результате почленного сложения у нас пропала переменная y.
В этом и состоит суть метода – избавиться от одной из переменных.
Теперь всё просто: 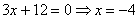
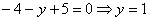
В чистовом оформлении решение должно выглядеть примерно так:
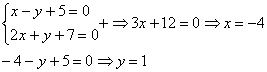
Пример 5:
Решить систему линейных уравнений:
В данном примере можно использовать «школьный» метод, но большой минус состоит в том, что когда мы будем выражать какую-либо переменную из любого уравнения, то получим решение в обыкновенных дробях. А возня с дробями займет время, к тому же, если у Вас не «набита рука» на действиях с дробями, то велика вероятность допустить ошибку.
Поэтому целесообразно использовать почленное сложение (вычитание) уравнений. Анализируем коэффициенты при соответствующих переменных:
Как видим, числа в парах (3 и 4), (4 и –3) – разные, поэтому, если сложить (вычесть) уравнения прямо сейчас, то от переменной мы не избавимся. Хотелось бы видеть в одной из пар одинаковые по модулю числа, например, 20 и 20 либо 20 и –20.
Будем рассматривать коэффициенты при переменной x:
Подбираем такое число, которое делилось бы и на 3 и на 4, причем оно должно быть как можно меньше. В математике такое число называется наименьшим общим кратным. Если Вы затрудняетесь с подбором, просто перемножьте коэффициенты: 3∙4 = 12.
Далее первое уравнение умножаем на число
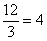
Второе уравнение умножаем на число 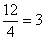
Вот теперь из первого уравнения почленно вычитаем второе.
На всякий случай приведём еще раз действия, которые проводятся мысленно:
Следует отметить, что можно было бы сделать и наоборот – из второго уравнения вычесть первое, это ничего не меняет. Начисто запишем:

Теперь подставим вычисленное значение переменной (y) в одно из уравнений системы. Например, в первое:
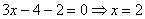
Ответ: 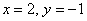
Решим систему другим способом. Рассмотрим коэффициенты при переменной (y):
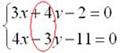
Очевидно, что вместо пары коэффициентов (4 и –3) нам нужно получить 12 и –12.
Для этого первое уравнение умножаем на 3, второе уравнение умножаем на 4:

Почленно складываем уравнения и находим значения переменных:
Ответ:
Пример 6:
Решить систему линейных уравнений:
Это пример для самостоятельного решения (ответ в конце урока).
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решение системы линейных уравнений методом сложения
Алгоритм решения системы линейных уравнений методом сложения
- Умножить обе части одного или обоих уравнений так, чтобы коэффициенты при одной из переменных стали противоположными (или равными) числами.
- Сложить (или отнять) уравнения, чтобы избавиться от одной из переменных.
- Решить второе уравнение относительно выраженной переменной.
- Решить полученное уравнение с одной переменной.
- Найти вторую переменную.
- Записать ответ в виде упорядоченной пары найденных значений переменных.
Умножаем первое уравнение на 2
Отнимаем от первого уравнения второе:
Находим y из первого уравнения:
В последовательной записи:
$$ <left< begin 3x+y = 5 | times 2 \ x+2y = 5 end right.> Rightarrow (-) <left< begin 6x+2y = 10 \ x+2y = 5 end right.> Rightarrow <left< begin 5x = 5 \ x+2y = 5 end right.> Rightarrow <left< begin x = 1 \ y = 5-3x = 2 end right.> $$
Примеры
Пример 1. Решите систему уравнений методом сложения:
$ а) <left< begin 5x-4y = 3 | times 2 \ 2x-3y = 4 | times 5 end right.> Rightarrow <left< begin 10x-8y = 6 \ 10x-15y = 20 end right.> Rightarrow <left< begin 7y = -14 \ 2x-3y = 4 end right.> Rightarrow <left< begin x = frac = -1 \ y=-2 end right.> $
$ б) <left< begin 4x-3y = 7 | times 3 \ 3x-4y = 0 | times 4 end right.> Rightarrow (-) <left< begin 12x-9y = 21 \ 12x-16y = 0 end right.> Rightarrow <left< begin 7y = 21 \ x = frac y end right.> Rightarrow <left< begin x = 4 \ y = 3 end right.> $
$ в) <left< begin 5a-4b = 9 | times 2 \ 2a+3b = -1 | times 5 end right.> Rightarrow (-) <left< begin 10a-8b = 18 \ 10a+15b = -5 end right.> Rightarrow <left< begin -23b = 23 \ a = frac end right.> Rightarrow <left< begin a = 1 \ b = -1 end right.> $
$ г) <left< begin 7a+4b = 5 \ 3a+2b = 1 | times (-2) end right.> Rightarrow (+) <left< begin 7a+4b = 5 \ -6a-4b = -2 end right.> Rightarrow <left< begin a = 3 \ b = frac end right.> Rightarrow <left< begin a = 3 \ b = -4 end right.>$
Пример 2. Найдите решение системы уравнений:
$$а) <left< begin frac-y = 7 \ 3x+ frac = 9 | times 2end right.> Rightarrow (+) <left< begin frac -y = 7 \ 6x+y = 18 end right.> Rightarrow <left< begin 6 frac x = 25 \ y = 18-6xend right.> Rightarrow $$
$$Rightarrow <left< begin x = 25: frac = 25 cdot frac = 4 \ y = 18-6 cdot 4 = -6 end right.> $$
$ в) <left< begin 3(5x-y)+14 = 5(x+y) \ 2(x-y)+9 = 3(x+2y)-16 end right.> Rightarrow <left< begin 15x-3y+14 = 5x+5y \ 2x-2y+9 = 3x+6y-16 end right.> Rightarrow $
$ г) <left< begin 5-3(2x+7y) = x+y-52 \ 4+3(7x+2y) = 23x end right.> Rightarrow <left< begin 5-6x-21y = x+y-52 \ 4+21x+6y = 23x end right.> Rightarrow <left< begin 7x+22y = 57 \ 2x-6y = 4 |:2 end right.>$
$$ Rightarrow <left< begin 7x+22y = 57 \ x-3y = 2 | times 7 end right.> Rightarrow (-) <left< begin 7x+22y = 57 \ 7x-21y = 14 end right.> Rightarrow <left< begin 43y = 43 \ x = 3y+2 end right.> Rightarrow <left< begin x = 5 \ y = 1 end right.>$$
Пример 3*. Найдите решение системы уравнений:
Введём новые переменные: $ <left< begin a = frac \ b = frac end right.> $
Перепишем систему и найдём решение для новых переменных:
$$ <left< begin2a+3b = 1| times 3 \ 3a-5b = 11 | times 2 end right.> Rightarrow (-) <left< begin 6a+9b = 3 \ 6a-10b = 22 end right.> Rightarrow <left< begin 19b = -19 \ a = frac end right.> Rightarrow <left< begin a = 2 \ b = -1 end right.> $$
Видео:Алгебра 7 Линейное уравнение с одной переменнойСкачать

10. Многочлены от одной переменной и действия над ними.
10.1. ОПРЕДЕЛЕНИЕ МНОГОЧЛЕНОВ ОТ ОДНОЙ ПЕРЕМЕННОЙ И ИХ ТОЖДЕСТВЕННОЕ РАВЕНСТВО
Рассмотрим одночлен и многочлен, которые зависят только от одной переменной, например от переменной х.
По определению одночлена числа и буквы (в нашем случае одна буква — х) в нем связаны только двумя действиями — умножением и возведением в натуральную степень. Если в этом одночлене произведение всех чисел записать перед буквой, а произведение всех степеней буквы записать как целую неотрицательную степень этой буквы (то есть записать одночлен в стандартном виде), то получим выражение вида ах n , где а — некоторое число. Поэтому одночлен от одной переменной х — это выражение вида ах п , где а — некоторое число, п — целое неотрицательное число. Если а 0, то показатель степени п переменной х называется степенью одночлена. Например, 25х 6 —одночлен шестой степени, — х 2 /3— одночлен второй степени. Если одночлен является числом, не равным нулю, то его степень считается равной нулю. Для одночлена, заданного числом 0, понятие степени не определяется (поскольку 0 = 0 • х = 0 • х 2 = 0 • х 3 . ).
По определению многочлен от одной переменной х — это сумма одночленов от одной переменной х (в которой приведены подобные слагаемые, то есть все одночлены-слагаемые имеют различную степень). Поэтому
Определение 1. Многочленом от одной переменной х называется выражение вида
Если аn 0, то этот многочлен называют многочленом п-й степени от переменной х. При этом член аnх п называют старшим членом многочлена f (х), число аn — коэффициентом при старшем члене, а член а0 — свободным членом. Например, 5х 3 — 2х + 1 — многочлен третьей степени, у которого свободный член равен 1, а коэффициент при старшем члене равен 5.
Заметим, что иногда нумерацию коэффициентов многочлена начинают с начала записи выражения (1), и тогда общий вид многочлена f (х) записывают так:
Т е о р е м а 1. Одночлены ах n , где а ≠ 0, и bx m , где b ≠ 0, тождественно равны тогда и только тогда, когда а = b и п = т.д.
Одночлен ах n тождественно равен нулю тогда и только тогда, когда а = 0.
Поскольку равенство одночленов
aх n = bх n (2)
выполняется при всех значениях х (по условию эти одночлены тождественно равны), то, подставляя в это равенство х = 1, получаем, что a = b. Сокращая обе части равенства (2) на a (где a ≠ 0 по условию), получаем x n =x m . При х = 2 из этого равенства имеем: 2 n = 2 m . Поскольку 2 n = 2• 2•. • 2 (n раз),
а 2 m = 2 • 2 •. • 2 (m раз), то равенство 2 n = 2 m возможно только тогда, когда n = m.
Таким образом, из тождественного равенства ax n = bx m (a 0, b 0) получаем, что a = b и n = m.
Если известно, что ax n = 0 для всех х, то при х = 1 получаем a = 0. Поэтому одночлен ax п тождественно равен нулю при a = 0 (тогда ax n = 0 • x n = 0).
Далее любой одночлен вида 0 • х n будем заменять на 0.
Т е о р ем а 2. Если многочлен f (x) тождественно равен нулю (то
есть принимает нулевые значения при всех значениях х), то все
его коэффициенты равны нулю.
Для доказательства используем метод математической индукции.
При n = 0 имеем f (х) = a0 = 0, поэтому a0 = 0. То есть в этом случае утверждение теоремы выполняется.
Предположим, что при n = k это утверждение также выполняется: если многочлен akх k + ak-1х k-1 + . + a1х + a0 тождественно равен 0, то
Докажем, что данное утверждение выполняется и при n = k + 1. Пусть
Поскольку равенство (3) выполняется при всех значениях х, то, подставляя в это равенство х = 0, получаем, что a0 = 0. Тогда равенство (3) обращается в следующее равенство: ak+1x k +1 + akx k + . + a1x = 0. Вынесем х в левой части этого равенства за скобки и получим
Равенство (4) должно выполняться при всех значениях х. Для того чтобы оно выполнялось при х 0, должно выполняться тождество ak+1x k + akx k -1 + . + a1 = 0.
В левой части этого тождества стоит многочлен со степенями переменной от х 0 до x k .Тогда по предположению индукции все его коэффициенты равны нулю: ak + 1 = ak = …= a1 = 0. Но мы также доказали, что a0 = 0,
поэтому наше утверждение выполняется и при n = k + 1. Таким образом, утверждение теоремы справедливо для любого целого неотрицательного n, то есть для всех многочленов.
Определение 2. Многочлен, у которого все коэффициенты равны нулю, обычно называют нулевым многочленом, или нуль-многочленом, и обозначают 0 (х) или просто 0 (поскольку 0 (х) = 0).
Теорема 3. Если два многочлена f (x) и g (x) тождественно равны,
то они совпадают (то есть их степени одинаковы и коэффициенты при одинаковых степенях равны).
Пусть многочлен f (х) = аnх n + аn-1х n — 1 + . + а2х 2 + а1х + а0, а многочлен g (x) = bmx m + bm — 1x m — 1 + . + b2x 2 + b1x + b0. Рассмотрим многочлен f (x) — g (x). Поскольку многочлены f (x) и g (x) по условию тождественно равны, то многочлен f (x) — g (x) тождественно равен 0. Таким образом, все его коэффициенты равны нулю.
Тогда a0 — b0 = 0, a1 — b1 = 0, а2 — b2 = 0, . . Отсюда a0 = b0, a1 = b1s а2 = b2, . . Как видим, если допустить, что у какого-то из двух данных многочленов степень выше, чем у второго многочлена (например, n больше m), то коэффициенты разности будут равны нулю. Поэтому начиная с (m + 1)-го номера все коэффициенты at также будут равны нулю. То есть действительно многочлены f (x) и g (x) имеют одинаковую степень и соответственно равные коэффициенты при одинаковых степенях.
Теорема 3 является основанием так называемого метода неопределенных коэффициентов. Покажем его применение на следующем примере.
Пример. Докажите, что выражение (х + 2)(х + 4)(х + 6)(х + 8) + 16 является полным квадратом.
Данное выражение может быть записано в виде многочлена четвертой степени, поэтому оно может быть полным квадратом только многочлена второй степени вида ах 2 + bх + с (а ≠ 0).
Раскрывая скобки в левой и правой частях этого тождества и приравнивая коэффициенты при одинаковых степенях х, получаем систему равенств. Этот этап решения удобно оформлять в следующем виде:
2-4-6 + 2-4-8 + 2-6-8 + 4-6-8 = 2bc
Из первого равенства получаем а = 1 или а = -1.
При а = 1 из второго равенства имеем b = 10, а из третьего — с = 20. Как видим, при этих значениях а, b и с последние два равенства также выполняются. Следовательно, тождество (5) выполняется при а = 1, b = 10, с = 20 (аналогично можно также получить а = -1, b = -10, с = -20).
1. Зная, что многочлены f (x) и g (x) тождественно равны, найдите значение
коэффициентов а, b, с, d:
3. Докажите тождество:
2)1+х 4 =(1+х +х 2 )(1-х +х 2 ).
4. Докажите, что данное выражение является полным квадратом:
5. Найдите такие а и b, чтобы при любых значениях х выполнялось равенство: 3х 4 + 4х 3 + 8х 2 + 3х + 2 = (3х 2 + ах + 1)(х 2 + х + b).
6. Запишите алгебраическую дробь 2/15х 2 +x-2 как сумму двух алгебраических дробей вида a/3x-1 и b/5x+2
10.2. ДЕЛЕНИЕ МНОГОЧЛЕНА НА МНОГОЧЛЕН С ОСТАТКОМ
Сложение и умножение многочленов от одной переменной выполняется с помощью известных правил сложения и умножения многочленов. В результате выполнения действий сложения или умножения над многочленами от одной переменной всегда получаем многочлен от той же переменной.
Из определения произведения двух многочленов вытекает, что старший член произведения двух многочленов равен произведению старших членов множителей, а свободный член произведения равен произведению свободных членов множителей. Отсюда получаем, что степень произведения двух многочленов равна сумме степеней множителей.
При сложении многочленов одной степени можно получить многочлен этой же степени или многочлен меньшей степени.
При сложении многочленов разных степеней всегда получаем многочлен, степень которого равна большей из степеней слагаемых.
Деление многочлена на многочлен определяется аналогично делению целых чисел. Напомним, что число а делится на число b (b≠ 0), если существует такое число q, что а = b • q.
Определение 3. Многочлен А (х) делится на многочлен В (х) (где В (х) —не нулевой многочлен), если существует такой многочлен Q (x), что
Как и для целых чисел, операция деления многочлена на многочлен выполняется не всегда, поэтому во множестве многочленов вводится операция деления с остатком
Разделить с остатком многочлен А (х) на многочлен В (х) (где В (х) — не нулевой многочлен) — это означает найти такую пару многочленов Q (x) и R (x), что А (х) = В (х) • Q (x) + R (x), причем степень остатка R (x) меньше степени делителя В (х) (в этом случае многочлен Q (х) называют неполным частным.)
Например, поскольку х 3 — 5х + 2 = (х 2 — 5) х + 2, то при делении многочлена х 3 — 5х + 2 на многочлен х 2 — 5 получаем неполное частное х и остаток 2.
Иногда деление многочлена на многочлен удобно выполнять «уголком», как и деление многозначных чисел, пользуясь следующим алгоритмом:
Алгоритм. При делении многочленов от одной переменной переменные в делимом и в делителе размещают по убыванию степеней и делят старший член делимого на старший член делителя. Потом полученный результат умножают на делитель, и это произведение вычитают из делимого. С полученной разностью выполняют аналогичную операцию: делят ее старший член на старший член делителя и полученный результат снова умножают на делитель и т. д. Этот процесс продолжают до тех пор, пока не получится в остатке 0 (если один многочлен делится на другой) или пока в остатке не получится многочлен, степень которого меньше степени делителя.
Докажем, что полученный результат действительно является результатом деления А (х) на В (х) с остатком.
Если обозначить результат выполнения первого шага алгоритма через f1 (x), второго шага — через f2 (x), третьего — через f3 (x), то операцию деления, выполненную выше, можно записать в виде системы равенств:
Сложим почленно равенства (1), (2), (3) и получим
Учитывая, что степень многочлена f3 (x) = х + 4 меньше степени делителя
В (х) = х 2 — 2х + 3, обозначим f3 (x) = R (x) (остаток), а х 2 — 3х — 8 = Q (x) (неполное частное). Тогда из равенства (4) имеем: А (х) = В (х) — Q (x) + R (x), то есть х 4 — 5х 3 + х 2 + 8х — 20 = (х 2 — 2х + 3)(х 2 — 3х — 8) + х + 4, а это и означает, что мы разделили А (х) на В (х) с остатком.
Очевидно, что приведенное обоснование можно провести для любой пары многочленов А (х) и В (х) в случае их деления столбиком. Поэтому описанный выше алгоритм позволяет для любых делимого А (х) и делителя В (х) (где В (х) — не нулевой многочлен) найти неполное частное Q (x) и остаток R (x).
То есть, имеет место следующая теорема.
Теорема 4. Для любой пары многочленов А (х) и В (х) (где В (х) — не нулевой многочлен) существует и притом единственная пара многочленов
Q(x) и R(x), такая, что А(х)=В(х)*Q(x) + R(x), причем сте-
пень R (x) меньше степени В (х) (или R (x) — нулевой многочлен).
Отметим, что в случае, когда степень делимого А (х) меньше степени делителя В (х), считают, что неполное частное Q (x) = 0, а остаток R (x) = А (х).
1.Выполните деление многочлена на многочлен:
1)3х 3 — 5х 2 + 2х — 8 на х — 2; 2) х 10 + 1 на х 2 + 1;
2. Выполните деление многочлена на многочлен с остатком:
1)4х 4 — 2х 3 + х 2 — х + 1 на x 2 + x + 2;
2)х 5 + х 4 + х 3 + х 2 + 1 на х 2 — х — 2.
3.При каких значениях а и b многочлен А (х) делится без остатка на многочлен В(х)?
4.Найдите неполное частное и остаток при делении многочлена А(х) на многочлен В(х) методом неопределенных коэффициентов:
10.3. ТЕОРЕМА БЕЗУ. КОРНИ МНОГОЧЛЕНА. ФОРМУЛЫ ВИЕТА
Рассмотрим деление многочлена f (x) на двучлен (х – а). Поскольку степень делителя равна 1, то степень остатка, который мы получим, должна быть меньше 1, то есть в этом случае остатком будет некоторое число R. Таким образом, если разделить многочлен f (x) на двучлен (х – а), то получим
Это равенство выполняется тождественно, то есть при любом значении х. При х = а имеем f (а) = R. Полученный результат называют теоремой Безу.
Те о р е м а 1 (теорема Безу). Остаток от деления многочлена f (х) на двучлен (х – а) равен f (а) (то есть значению многочлена при х = а).
Задача 1. Докажите, что х 5 – 3х 4 + 2х 3 + 4х – 4 делится на х – 1 без остатка.
- Подставив в f (х) = х 5 – 3х 4 + 2х 3 + 4х – 4 вместо х значение 1, получаем: f (1) = 0. Таким образом, остаток от деления f (х) на (х – 1) равен 0, то есть f (x) делится на (х – 1) без остатка.
О п р е д е л е н и е. Число α называют корнем многочлена f (x), если f (α) = 0.
Если многочлен f (х) делится на (х – α), то α — корень этого многочлена.
- Действительно, если f (х) делится на (х – α), то f (х) = (х – α)*Q (x) и поэтому f (α) = (α – α)*Q (α) = 0. Таким образом, α — корень многочлена f (х).
Справедливо и обратное утверждение. Оно является следствием теоремы Безу.
Т е о р е м а 2. Если число α является корнем многочлена f (x), то этот многочлен делится на двучлен (х – α) без остатка.
- По теореме Безу остаток от деления f (x) на (х – α) равен f (α). Но по условию α — корень f (x), таким образом, f (α) = 0.
Обобщением теоремы 2 является следующее утверждение.
Те о р е м а 3. Если многочлен f (x) имеет попарно разные корни α1, α2, . αn, то он делится без остатка на произведение
- Для доказательства используем метод математической индукции.
При n= 1 утверждение доказано в теореме 2. Допустим, что утверждение справедливо при n = k. То есть если α1, α2, . αk — попарно разные корни многочлена f (x), то он делится на произведение (х – α1)(х – α2)*…*(х – αk). Тогда
Докажем, что утверждение теоремы справедливо и при n = k + 1. Пусть α1, α2, . αk, αk + 1 — попарно разные корни многочлена f (x). Поскольку αk + 1 — корень f (x), то f (αk + 1) = 0.
Принимая во внимание равенство (1), которое выполняется согласно предположению индукции, получаем:
По условию все корни α1, α2, . αk, αk + 1 разные, поэтому ни одно из чисел αk + 1 – α1, αk + 1 – α2, . αk + 1 – αk не равно нулю. Тогда Q (αk + 1) = 0. Таким образом, αk + 1 — корень многочлена Q (x). Тогда по теореме 2 Q (x) делится на (х – αk + 1), то есть Q (x) = (х – αk + 1)*Q1 (x) и из равенства (1) имеем
Это означает, что f (х) делится на произведение
то есть теорема доказана и при n = k + 1.
Таким образом, теорема справедлива для любого натурального n.
С л е д с т в и е. Многочлен степени n имеет не больше n разных корней.
Пусть теперь многочлен n-й степени f (x) = аnх n + аn– 1 х n –1 + . + а2х 2 + а1х + а0 (an ≠ 0) имеет n разных корней α1, α2, . αn. Тогда этот многочлен делится без остатка на произведение (х – α1)(х – α2)*. *(х – αn). Это произведение является многочленом той же n-й степени. Таким образом, в результате деления можно получить только многочлен нулевой степени, то есть число. Таким образом,
Если раскрыть скобки в правой части равенства (2) и приравнять коэффициенты при старших степенях, то получим, что b = аn, то есть
Сравнивая коэффициенты при одинаковых степенях х в левой и правой частях тождества (3), получаем соотношения между коэффициентами уравнения и его корнями, которые называют формулами Виета:
Например, при n = 2 имеем:
| a1+a2+a3= — a2/a3; |
 |
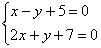
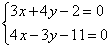
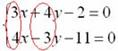
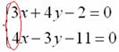
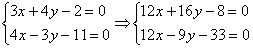
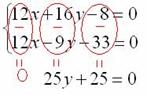
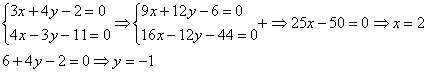
.jpg)















 имеет точно три корня.
имеет точно три корня. не имеет решений.
не имеет решений. имеет единственное решение.
имеет единственное решение.

 имеет три действительных корня, которые образуют геометрическую прогрессию?
имеет три действительных корня, которые образуют геометрическую прогрессию?
















