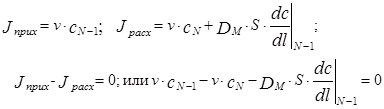Почему для решения уравнения диффузионной модели его обычно сначала приводят к безразмерному виду

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Диффузионная модель

Поршневой режим движения жидкостей, рассмотренный нами при выводе уравнения модели идеального вытеснения, в реальных процессах реализуется не всегда. На самом деле в реальных процессах жидкость в различных направлениях перемещается за счет следующих явлений:

· Поперечной неравномерности профиля скорости.

· Пристеночных эффектов, каналообразования.

· Переноса за счет молекулярной диффузии.

Будем считать, что все отклонения режима движения от поршневого могут быть сведены к переносу в обратном направлении за счет влияния конвективной диффузии, или осевой дисперсии.

Составим при этих допущениях уравнение материального баланса для элементарного объема проточного аппарата подобного аппарату идеального вытеснения, только с учетом диффузии в обратном направлении. На рис 3.10. приведена схема потоков в таком аппарате:

Рис.3.4.1. Схема потоков в аппарате, описываемом диффузионной моделью.

V=S×L – объем аппарата, S=p×d 2 /4 – площадь поперечного сечения, L – длина аппарата. Стрелками в обратном направлении обозначен перенос вещества в обратном направлении за счет конвективной диффузии или продольной дисперсии.

Поток вещества за счет турбулентной диффузии описывается уравнением, подобным уравнению диффузии Фика:

(3.4.1)

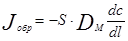
Где J_обр— поток вещества в обратном направлении.

D_M – коэффициент обратного переноса массы за счет турбулентной диффузии.

Составим уравнение материального баланса для элементарного объема аппарата, ограниченного сечениями j-1 и j+1, расположенными на расстоянии Dl.

Приход вещества в рассматриваемый объем складывается из прихода за счет конвективного переноса, равного произведению v×c_j-1 и приходу за счет обратного потока из предшествующего объема аппарата:

(3.4.2)

Накопление массы в рассматриваемом элементарном объеме будет равно интегралу от разности входящего и выходящего потоков в объем:

(3.4.3)

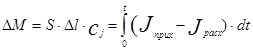
Перейдем теперь от накопления массы в объеме к изменению концентрации. Для этого разделим обе части уравнения на величину элементарного объема

DV=S×Dl и продифференцируем обе части уравнения по времени. Уравнение принимает следующий вид, с учетом того, что производная от интеграла по аргументу равна подинтегральному выражению и с учетом выражений уравнения (3.4.2) для потоков прихода и расхода вещества:

(3.4.4)

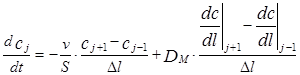
Рассмотрим пределы слагаемых правой части уравнения (3.4.4) при Dl®0.

(3.4.5)

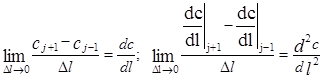
Подставив выражения пределов из (3.4.5) в (3.4.4) получим окончательно уравнение диффузионной модели в следующем виде:

(3.4.6)

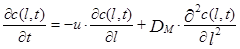
Уравнение записано как дифференциальное уравнение в частных производных, так как концентрация является функцией двух независимых переменных с(l,t). В дальнейшем мы не будем это писать для сокращения записей но будем постоянно иметь в виду, что с=с(l,t).

Приведем уравнение к безразмерному виду с помощью следующих подстановок:

x=l/L, где l – текущая длина, а L – полная длина аппарата. Тогда Ldx=dl и dl 2 =L 2 dx 2 . С использованием этих подстановок уравнение диффузионной модели может быть преобразовано к следующему виду:

(3.4.7)

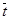
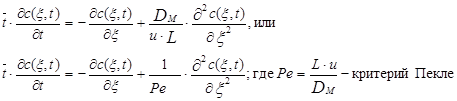
Умножим обе части уравнения (3.4.7) на величину L/u= — среднее время пребывания в аппарате. В итоге получим:

(3.4.8)

Рассмотрим предельное выражение уравнения диффу4зионной модели при Ре® ¥. При Ре® ¥ 1/Ре®0. Таким образом уравнение диффузионной модели превращается в следующее уравнение:

, которое является уравнением модели идеального вытеснения.

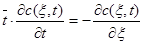
Для решения уравнения диффузионной модели преобразуем его по Лапласу по переменной t. В итоге получим:

(3.4.9)

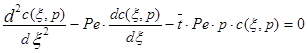
Уравнение (3.4.9) представляет собой однородное обыкновенное дифференциальное уравнение с постоянными коэффициентами. Для его решения необходимо решить характеристическое уравнение, в котором К есть d/dx. Характеристическое уравнение для уравнения (3.4.9) будет иметь вид:

K 2 -Pe×K- 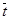×Pe×p=0 (3.4.10)

Найдем корни характеристического уравнения в следующем виде:

(3.4.11)

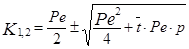
Обозначим первое слагаемое в уравнении (3.4.1) через a, а второе через b.

Тогда корни характеристического уравнения можно записать в следующем виде: К₁ = a+b, К₂ = a — b . Тогда общее решение уравнения (3.4.9) для случая когда К₁ ¹ К₂ (корни различные и действительные) можно записать в виде:

(3.4.12)

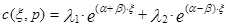
где -l₁ и l₂ – постоянные интегрирования, определяемые из граничных условий.

Если К₁ = К₂ (корни равные и действительные)

(3.4.13)

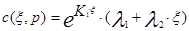
Если корни комплексные К_1,2=a±i×b — a- действительная часть, i×b -мнимая часть, то решение имеет вид:

(3.4.14)

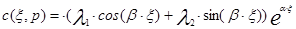
Найдем граничные условия для аппарата конечных размеров. Для этого составим уравнение материального баланса для входной ячейки аппарата, указанной на схеме рис.3.4.1. Приход массы в эту ячейку складывается из прихода с входным потоком и прихода за счет обратного диффузионного потока. Расход складывается из конвективного уноса массы в последующие объемы аппарата.

Для установившегося режима можно считать, что накопления массы во входном сечении аппарата не происходит и J_прих=J_расх. Устремим рассматриваемый входной объем к нулю, В этом случае с₁®с₀, и уравнение для граничного условия принимает вид:

(3.4.15)

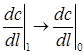
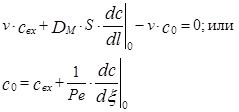
Таким образом, из уравнения (3.4.15) следует, что концентрация вещества во входном сечении аппарата не равна концентрации во входном потоке, Она изменяется скачкообразно за счет действия обратного перемешивания.

Рассмотрим теперь вывод уравнения граничного условия для второй, выходной границы аппарата. Для этой границы мы также составим уравнение материального баланса при условии отсутствия накопления массы в выходном сечении аппарата.

При Dl®0 c_N-1®c_N откуда следует, что

(3.4.16)

Для определения постоянных интегрирования нужно подставить в уравнения (3.4.15) и (3.4.16) значения функции (3.4.12) при x=0 и x=1 и ее производных при этих же значениях аргумента. Для получения значения производной продифференцируем уравнение (3.4.12) по x. В итоге получим следующее уравнение:

(3.4.17)

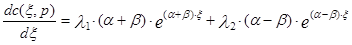
Подставим выражение для производных и функций в уравнения граничных условий, получим следующие выражения для постоянных интегрирования:

(3.4.18)

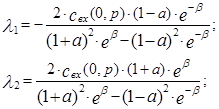
где a=b¤a

Подставив найденные выражения для постоянных интегрирования в уравнение (3.4.12), найдем уравнение для зависимости концентрации от длины и переменной Лапласа в следующем виде:

(3.4.19)

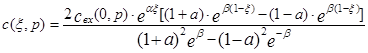
Найдем передаточную функцию аппарата с конечными размерами. Для этого вычислим значение выходной концентрации, положив в уравнении (3.4.19) x=1.

В итоге получим:

(3.4.20)

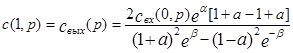
откуда найдем передаточную функцию:

(3.4.21)

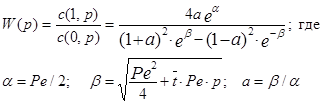
Критерий Пекле Pe и коэффициент продольной диффузии D_M, являющиеся параметрами диффузионной модели определяют экспериментально с использованием экспериментов с трассерами. Методы определения параметров модели по экспериментальным данным мы рассмотрим ниже.

Рассмотрим решение уравнения диффузионной модели для аппарата бесконечно больших размеров. В таком аппарате возмущения не доходят до его границ. Поэтому можно считать, что концентрация на входе в аппарат равна концентрации во входном потоке, а концентрация на выходе равна нулю, при L®¥. Для этого случая граничные условия будут иметь вид:

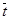
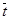
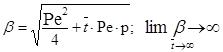
с_вх(р)=с(0,р); с(1,р)®0, так как ®¥. Рассмотрим пределы для переменных a и b при ®¥.

, следовательно e ( a — b ) ®0, поэтому второй член выражения (3.4.12) l₂e -( a — b ) ®0, тогда l₂¹0. Для того чтобы выполнялось второе граничное условие l₁e ( a + b ) +l₂e ( a — b ) =0, необходимо, чтобы член l₁e ( a + b ) был равен нулю. Следовательно, l₁=0. Для нахождения второй постоянной интегрирования l₂ воспользуемся первым граничным условием при x=0, учитывая, что

или при x=0 получим:

Окончательно будем иметь:

с(x,р)=с_вх(р) e ( a — b ) x (3.4.22)

Концентрация на выходе из аппарата будет равна:

Откуда передаточная функция аппарата бесконечно больших размеров будет равна:

(3.4.24)

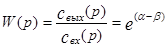
Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Однопараметрическая диффузионная модель

Объекты, описываемые этой моделью, как и моделью идеального вытеснения, относятся к объектам с распределенными параметрами. Схематическое изображение потока, в котором движение фазы представляется однопараметрической диффузионной гидродинамической моделью, приведено на рис. 2.3.

В этом случае наряду с конвективными потоками компонентов (/=. «), как это было показано для гидродинамической модели

Рис. 2.3. Диффузионная однопараметрическая модель

идеального вытеснения, существуют и обратные диффузионные потоки (со знаком «минус»).

Частичное перемещение фазы навстречу конвективному потоку (так называемое «обратное перемешивание») описывается уравнением потока, аналогичным уравнению молекулярной диффузии (закон Фика), в котором коэффициент диффузии D_L называют коэффициентом продольного перемешивания.

Динамическая модель. Уравнение покомпонентного баланса с учетом того, что уравнение молекулярной диффузии описывается второй производной по пространственной координате, может быть представлено для динамического режима рассматриваемого объекта следующем образом.

Уравнения покомпонентных балансов:

Уравнение общего материального баланса ^Х/=1 :

Уравнение теплового баланса записывается подобно уравнениям покомпонентных балансов с учетом замены х_;. на c_pt в покомпонентных балансах:

В результате для математического описания зоны потока, которая может быть представлена однопараметрической диффузионной гидродинамической моделью, получена система дифференциальных уравнений в частных производных второго порядка. Полученная система должна быть дополнена зависимостями для физико-химических коэффициентов элементарных процессов. В результате решения системы должна быть получена функция двух независимых переменных — времени t и пространственной координаты /.

Следует отметить, что в отличие от модели идеального вытеснения, процедура решения здесь оказывается более сложной, так как в данном случае приходится решать систему дифференциальных уравнений в частных производных второго порядка, тогда как в случае модели идеального вытеснения решается эта система уравнений первого порядка. Кроме того, для решения требуется определить коэффициент продольного перемешивания D_L, что связано с проведением специальных экспериментов.

Статическая модель. При описании стационарных режимов объектов, движение потока фазы которых представляется однопараметрической диффузионной гидродинамической моделью, производные по времени в системе уравнений, описывающей динамические режимы (2.25)—(2.27), равны нулю. Поэтому для случая однопараметрической диффузионной модели полученная СДУЧП (2.20), для описания стационарных режимов преобразуется в систему обыкновенных дифференциальных уравнений с одной независимой переменной — пространственной координатой /.

Уравнения покомпонентных балансов:

Уравнение общего материального баланса ^*,=1 :

Уравнение теплового баланса записывается подобно:

Так как объекты, движение фаз которых описывается однопараметрическими диффузионными гидродинамическими моделями, также относятся к объектам с распределенными параметрами, общий вид решений не будет отличаться от решений, получаемых при описании гидродинамики процесса моделью идеального вытеснения.

Однако поскольку в этом случае решается система уравнений второго порядка, алгоритм решения оказывается более сложным, и, кроме того, возникает задача определения коэффициента продольного перемешивания D_L путем проведения специальных экспериментов.

Видео:Составить дифференциальные уравнения семейств линийСкачать

Двухпараметрическая диффузионная модель

Используют также двухпараметрическую диффузионную модель, в которой параметры рассматриваются как функции не только длины аппарата, но и его радиального измерения (добавляется член D_{r д}

—R—г—— , учитывающий радиальное перемешивание). Запи- RL oR oR )

шем уравнения покомпонентных балансов:

В уравнения общего материального и теплового балансов также добавляется член, учитывающий радиальное перемешивание.

В уравнениях (2.25)—(2.31) для диффузионных моделей часто используют критерий Пекле (1.60), который имеет вид Pe_L =—- для

продольной и Pe_R =-для радиальной диффузии. При этом даже

стационарный режим потока описывается уже дифференциальным уравнением в частных производных второго порядка, решение которого довольно сложно.

Видео:Частное решение дифференциального уравнения. 11 класс.Скачать

Ячеечная модель

Основой модели является представление об идеальном перемешивании в пределах ячеек, расположенных последовательно, и в отсутствии перемешивания между ячейками (табл. 2.1). Параметром, характеризующим модель, служит число ячеек N. Математическое описание ячеечной модели состоит из N линейных дифференциальных уравнений первого порядка — в соответствии с числом ячеек идеального перемешивания:

Уравнения модели идеального смешения (2.16)—(2.18) рассмотрены выше. При N = 1 ячеечная модель переходит в модель идеального смешения, а при N = °° — в модель идеального вытеснения.

Из изложенных выше моделей потоков следует, что для решения прямых задач математического моделирования ХТП необходимо располагать основными алгоритмами решения систем обыкновенных дифференциальных уравнений и уравнений в частных производных.

Видео:ДУ Уравнения, не разрешенные относительно производнойСкачать

Диффузионные модели. Различают однопараметрическую и двухпараметрическую диффузионные модели.

Однопараметрическая модель. Ее основой является модель идеального вытеснения, осложненная обратным перемешиванием, подчиняющимся формальному закону диффузии. Параметром, характеризующим модель, служит коэффициент турбулентной диффузии, или коэффициент продольного перемешивания D_L.

При составлении однопараметрической диффузионной модели принимаются следующие допущения: изменение концентрации субстанции является непрерывной функцией пространственной координаты; концентрация субстанции в данном сечении постоянна; объемная скорость потока и коэффициент перемешивания не изменяются по длине и сечению потока.

При таких допущениях модель описывается уравнением

Член уравнения учитывает турбулентную диффузию, или продольное перемешивание. Величина D_L определяется расчетным или опытным путем.

Двухпараметрическая модель. В этой модели учитывается перемешивание потока в продольном и радиальном направлениях; причем модель характеризуется коэффициентом продольного (D_L) и радиального (D_R) перемешивания. При этом принимается, что величины D_L и D_R не изменяются по длине и сечению аппарата, а скорость потока постоянна.

При условии движения потока в аппарате цилиндрической формы радиуса R с постоянной по длине и сечению скоростью уравнение двухпараметрической модели имеет вид

При опытном определении коэффициентов продольного и радиального перемешивания (D_L и D_R) обычно их представляют в виде безразмерных комплексов — критериев Пекле: или , где L — определяющий линейный размер системы. Тогда уравнение диффузионной модели также приводится к безразмерному виду. С этой целью вводятся безразмерная концентрация ; безразмерная длина и время .

Учитывая, что объемная скорость принимается постоянной, для установившегося режима уравнение (2.8) приводится к виду

Если , диффузионная модель переходит в модель идеального вытеснения; если — в модель идеального перемешивания.

Ячеечная модель. Основой модели является представление об идеальном перемешивании в пределах ячеек, расположенных последовательно, и в отсутствии перемешивания — между ячейками. Параметром, характеризующим модель, служит число ячеек N.

Математическое описание ячеечной модели включает N линейных дифференциальных уравнений первого порядка:

где i =1, 2, . N (N — номер ячейки);

Ячеечной моделью оценивают функции распределения в последовательно соединенных аппаратах с мешалками, осуществляющими интенсивное перемешивание.

Кривые отклика при ступенчатом или импульсном возмущении для различных типов гидродинамических моделей представлены в табл. 2.1.

Таблица 2.1Типовые модели структуры потоков в аппарате

🔥 Видео

11. Уравнения в полных дифференциалахСкачать

Общее, частное и особое решение ДУ. ПримерСкачать

Не разрешенные относительно производной 1Скачать

Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

12. Интегрирующий множитель. Уравнения в полных дифференциалахСкачать

Применение степенных рядов к решению дифференциальных уравнений.Скачать

6. Особые решения ДУ первого порядкаСкачать

Разностное функциональное уравнение решено двумя способами.Скачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Дифференциальные уравнения за 8 часовСкачать

Геометрический смысл дифференциального уравненияСкачать

Операционное исчисление. Решить неоднородное дифференциальное уравнение 2 порядкаСкачать