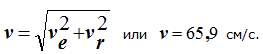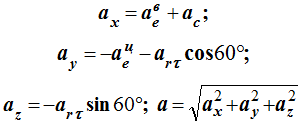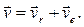Теоретическая механика: Решебник Яблонского:
Сложное движение (К7, К8)

Бесплатный онлайн решебник Яблонского. Выберите задание и номер варианта для просмотра решения. Смотрите также способы и примеры решения задач по темам сложное движение точки и тела и кинематика механизмов.

Видео:Cложное движение точки. ТермехСкачать

Задание К.7. Определение абсолютной скорости и абсолютного ускорения точки

Точка M движется относительно тела D. По заданным уравнениям относительного движения точки M и движения тела D определить для момента времени t=t₁ абсолютную скорость и абсолютное ускорение точки M.

Схемы механизмов показаны на рис. 99–101, а необходимые для расчета данные приведены в табл. 34.

Примечания. Для каждого варианта положение точки M на схеме соответствует положительному значению s_r; в вариантах 5, 10, 12, 13, 20–24, 28–30 OM=s_r – дуга окружности; на схемах 5, 10, 12, 21, 24 OM – дуга, соответствующая меньшему центральному углу. Относительное движение точки M в вариантах 6 и 27 и движение тела D в вариантах 23 и 29 определяются уравнениями, приведенными в последнем столбце табл. 34.

Варианты с решением: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 (решено 100%)

Видео:Динамика относительного движения точки.Скачать

Задание К.8. Определение угловых скоростей звеньев планетарного редуктора

Найти угловые скорости ведомого вала II и сателлитов редуктора. Схемы редукторов показаны на рис. 104–106, необходимые для расчета данные приведены в табл. 36.

Примечания. Положительный и отрицательный знаки угловых скоростей означают соответственно направление вращения против и по часовой стрелке, если смотреть со стороны ведущего вала I (для редуктора с цилиндрическими колесами) или со стороны положительного направления соответствующей оси (для редуктора с коническими колесами).

В вариантах 26 и 28 использованы численные данные из сборника 2006 г. издания. В сборнике 1985 г. численные данные для этих двух вариантов поменяны местами относительно более нового издания, а схемы редукторов те же самые. Поэтому если вам нужно сделать подсчеты по изданию 1985 г. (или любого другого, где задания отличаются только значениями величин) – просто подставьте свои числа в формулы из решения нужного варианта.

Видео:К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать

iSopromat.ru

Пример определения для заданного момента времени абсолютной скорости и абсолютного ускорения точки по заданным уравнениям относительного движения точки и треугольника вращающегося вокруг оси.

Видео:Урок 19. Относительность движения. Формула сложения скоростей.Скачать

Задача

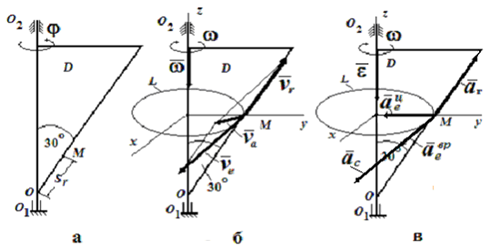
Треугольник D вращается вокруг оси O₁O₂ (рис. 1, а). По стороне треугольника движется точка M. По заданным уравнениям относительного движения точки M и движения треугольника D определить для момента времени t= t₁ абсолютную скорость и абсолютное ускорение точки M.

Видео:Решение графических задач на равномерное движениеСкачать

Решение

Точка M совершает сложное движение. Движется относительно треугольника D и вместе с треугольником вращается вокруг оси O₁O₂. Тогда движение точки относительно треугольника будет относительным, движение вместе с треугольником – переносным.

Будем считать, что в заданный момент времени плоскость чертежа совпадает с плоскостью треугольника D. Положение точки M на треугольнике D определяется расстоянием s_r= OM.

Абсолютную скорость точки М найдем как геометрическую сумму относительной и переносной скоростей:

Модуль относительной скорости v_r = | v_r |, где

v_r= ds_r/dt = 24π sin(3π t) — алгебраическое значение относительной скорости.

Положительный знак у v_r показывает, что вектор v_r направлен в сторону возрастания s_r.

Модуль переносной скорости

где R – радиус окружности L, описываемой той точкой тела, с которой в данный момент совпадает точка М;
R = s_rsin 30° = 10,0 см;
ω_e – модуль угловой скорости тела

Отрицательный знак у величины ω_e показывает, что вращение треугольника происходит вокруг оси Oz в сторону, обратную направлению отсчета угла φ. Поэтому вектор ω_e направлен по оси Oz вниз (рис. 1, б).

Модуль переносной скорости по формуле (1)

Вектор v_e направлен по касательной к окружности L в сторону вращения тела.

Так как v_e и v_r взаимно перпендикулярны, модуль абсолютной скорости точки М

Абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова ускорений

или в развернутом виде

Модуль относительного касательного ускорения

Отрицательный знак a_rτ показывает, что вектор a_rτ направлен в сторону отрицательных значений s_r. Знаки v_r и a_rτ различны, следовательно, относительное движение точки М замедленное.

Относительное нормальное ускорение

так как траектория относительного движения – прямая ( ρ = ∞).

Модуль переносного вращательного ускорения

где ε_е = | ε_е | – модуль углового ускорения тела D

Знаки ε_е и ω_e одинаковы; следовательно, вращение треугольника D ускоренное, направления векторов ε_е и ω_e совпадают (рис. 1, б, в).

Согласно (2) a_e в = 102 см/с 2 . Вектор a_e в направлен в ту же сторону, что и вектор v_e.

Модуль переносного центростремительного ускорения

Вектор a ц _e направлен к центру окружности L.

Модуль кориолисова ускорения

С учетом найденных выше значений ω_e и v_r получаем

Вектор a_C направлен, согласно правилу векторного произведения, к нам — перпендикулярно плоскости треугольника D (рис. 1, в).

Модуль абсолютного ускорения точки М находим способом проекций:

Результаты расчета сведены в таблицу 1.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Урок 7. Механическое движение. Основные определения кинематики.Скачать

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Видео:Кинематика точки Задание К1Скачать

VI. Определение абсолютной скорости

И абсолютного ускорения точки. Задание К.5.

Точка М движется относительно тела D. По заданным уравнениям относительного движения точки М и движения тела D определить для момента времени t = t₁ абсолютную скорость и абсолютное ускорение точки М.

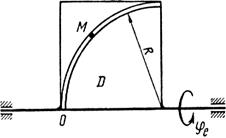
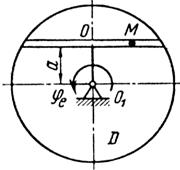
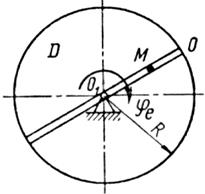
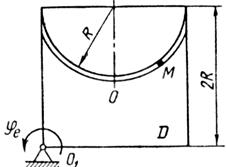
Схемы механизмов показаны на рис. 26-28, а необходимые для расчета данные приведены в табл. 10.

Пример выполнения задания. Дано: схема механизма (рис. 29),

s_r = OM = 16 — 8 cos (3πt) см; φ_с=0,9t 2 -9t 3 рад; t₁=2,9 c.

Решение. Будем считать, что в заданный момент времени плоскость чертежа (рис. 29) совпадает с плоскостью треугольника D. Положение точки М на теле D определяется расстоянием s_r = ОМ.

Абсолютную скорость точки М найдем как геометрическую сумму относительной и переносной скоростей:

Модуль относительной скорости ,

.

=65,2 см/с; v_r = 65,2 см/с.

Положительный знак у показывает, что вектор направлен в сторону возрастания s_r.

Модуль переносной скорости

где R — радиус окружности L, описываемой той точкой тела, с которой в данный момент совпадает точка М, R = s_r sin 30° = 10,0 см; ω_e, – модуль угловой скорости тела:

ω_е = | |; = dφ_е/dt= 1,8t – 27t 2 .

= -0,93 рад/с; ω_е = 0,93 рад/с.

Отрицательный знак у величины показывает, что вращение треугольника происходит вокруг оси Oz в сторону, обратную направлению отсчета угла φ. Поэтому вектор ω_е направлен по оси Oz вниз (рис. 30, а).

Таблица 10

Номер варианта (рис. 26-28)	Уравнение относительного движения точки М OM=sк=sк(t) см	Уравнение движения тела	t1, с	R, см	а, см	α, град	Дополнительные данные
φe=φe(t), рад	xe=xe(t), см
18sin(πt/4)	2t 3 -t 2	—	2 /3	—	—
20sin(πt)	0,4t 2 +t	—	5 /3	—	—
6t 3	2t+ 0,5t 2	—	—	—
10sin(πt/6)	0,6t 2	—	—	—
40π соз(πt/6)	3t-0,5t 3	—	—	—
—	—	3t+0,27t 3	10 /3	—	—	φr=0,15π/t 3
20cos(2πt)	0,5t 2	—	3 /8	—
6(t+0,5t 2 )	t 3 -5t	—	—	—
10(1+sin(2πt)	4t+1,6t 2	—	1 /8	—	—	—
20π соs(πt/4)	1,2t-t 2	—	4 /3	—
25sin(πt/3)	2t 2 -0,5t	—	—	—
15πt 3 /8	5t-4t 2	—	—
120πt 2	8t 2 -3t	—	1 /3	—	—
3+14sin(πt)	4t-2t 2	—	2 /3	—	—
3π(t 2 +t)	0,2t 3 +t	—	—
20sin(πt)	t-0,5t 2	—	1 /3	—	—
8t 3 +2t	0,5t 2	—	—		—
10t+t 3	8t-t 2	—	—	—
6t+4t 3	t+3t 2	—	—	—
30π соs(πt/6)	6t+t 2	—	—	—
25π(t+t 2 )	2t-4t 2	—	1 /2	—	—
10π sin(πt/4)	4t-0,2t 2	—	1 /3	—	—
6πt 2	—	—	—	—	φ=5πt 3 /6; О1О=О2А=30 см
75π(0,1t+0,3t 3 )	2t-0,3t 2	—	—	—
15sin(π/t 3 )	10t-0,1t 2	—	—	—	—
8cos(π/t 2 )	-2πt 2	—	3 /2	—	—
—	—	50t 2	—	—	φr=5πt 3 /48
2,5πt 2	2t 3 -5t	—	—	—
5πt 3 /4	—	—	—	—	φ=πt 3 /8; О1О=О2А=40 см
4πt 2	—	t 3 +4t	—	—

Примечания. Для каждого варианта положение точки M на схеме соответствует положительному значению s_r; в вариантах 5, 10, 12, 13, 20—24, 28 — 30 OM= s_r —дуга окружности; на схемах 5, 10, 12, 21, 24 ОМ — дуга, соответствующая меньшему центральному- углу. Относительное движение точки M в вариантах 6 и 27 и движение тела D в вариантах 23 и 29 определяются уравнениями, приведенными в последнем столбце табл. 10.

Рис. 26.

Рис. 27.

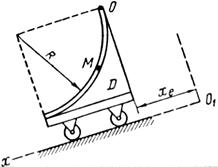Рис. 28.

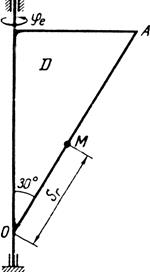	Модуль переносной скорости, по формуле (1), ve = 9,3 см/с. Вектор направлен по касательной к окружности L в сторону вращения тела. Так как и взаимно перпендикулярны, модуль абсолютной скорости точки М , v = 65,9 см/с. Абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова ускорений: , или в развернутом виде
Рис. 29

Модуль относительного касательного ускорения

где

При t = 2 /₉ c. = –355 см/с 2 ; = 355 см/с 2 .

Отрицательный показывает, что вектор направлен в сторону отрицательных значений s_r. Знаки и одинаковы; следовательно, относительное движение точки М ускоренное.

🎬 Видео

Термех. Кинематика. Сложное движение точкиСкачать

Определение абсолютной скорости и абсолютного ускорения точкиСкачать

Сложное движение точкиСкачать

Динамика относительного движенияСкачать

13.7. Относительное движениеСкачать

Сложное движение точки. Решение задачи. Авторы: Ермишин Степан, Ходунов Алексей, Хужаев ДмитрийСкачать

Кинематика. 4.3. Сложное движение точки на примере диска. Определение абсолютной скорости точки.Скачать

Теоретическая механика. Задание К7 (часть 3) из сборника ЯблонскогоСкачать

Теоретическая механика. Задание К7 (часть 1) из сборника ЯблонскогоСкачать

Д1 Дифференциальные уравнения движения материальной точкиСкачать

Сложное движение точки #1Скачать

Плоско-параллельное движение. Определение скоростей. ТермехСкачать

кинематика точкиСкачать