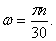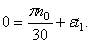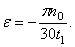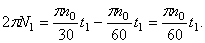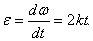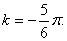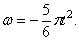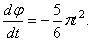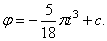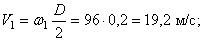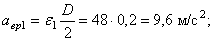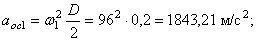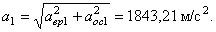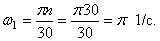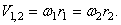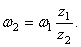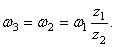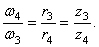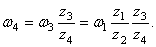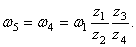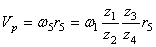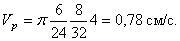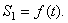По заданному уравнению вращения твердого тела

Видео:Вращательное движение. 10 класс.Скачать

По заданному уравнению вращения твердого тела

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ

Кинематика вращения тела вокруг неподвижной оси

1. Краткие сведения из теории

Уравнение вращательного движения твердого тела вокруг неподвижной оси имеет вид

. (40)

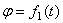
Отсчет угла ведется от выбранного начала. При этом углам, отложенным в направлении движения часовой стрелки, придается знак “минус”, а углам противоположного направления – знак “плюс”.

Угол поворота выражается в радианах. Иногда угол поворота определяется числом оборотов N. Зависимость между и N следующая .

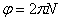
Угловая скорость тела:

(41)

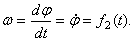
Знак производной 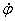дает возможность установить происходит ли вращение тела в положительном направлении отсчета угла поворота (знак “плюс”) или в обратную сторону (знак “минус”). Единица измерения угловой скорости – радиан в секунду (или 1/с).

Иногда угловую скорость характеризуют числом оборотов в минуту и обозначают буквой n . Зависимость между и n имеет вид

Угловое ускорение тела:

(42)

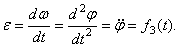
Знак производной 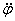дает возможность установить является ли вращение тела в данный момент времени ускоренным или замедленным. Если знаки и одинаковы, тело вращается ускоренно, а если их знаки различны – замедленно. Единица измерения углового ускорения – радиан на секунду в квадрате (или 1/с 2 ).

Траекториями точек тела, не лежащих на оси вращения, являются окружности с центрами на оси вращения и радиусами, равными кратчайшему расстоянию от этих точек до оси вращения.

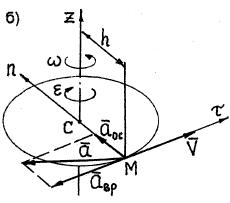
Модуль скорости любой точки тела, находящейся на расстоянии h от оси вращения (рис. 18), определяется по формуле

. (43)

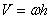
Направлена скорость точки по касательной к описываемой точкой окружности в сторону движения.

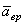
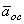
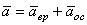
Ускорение любой точки тела состоит из двух составляющих – вращательного и осестремительного ускорений:

.

Модуль вращательного ускорения точки определяется по формуле

. (44)

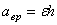
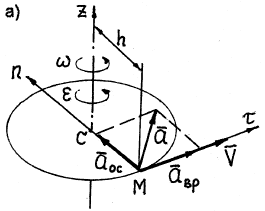
Вращательное ускорение направлено по касательной к описываемой точкой окружности в ту же сторону, что и его скорость, если вращение тела ускоренное (рис. 18, а) и в сторону, противоположную скорости, если вращение замедленное (рис.18, б).

Модуль осестремительного ускорения определяется по формуле

. (45)

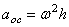
Осестремительное ускорение всегда направлено по радиусу окружности от точки к центру окружности (рис. 18).

Модуль полного ускорения точки определяется по формуле

(46)

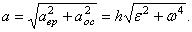
2. Основные типы задач кинематики вращения тела вокруг оси

В зависимости от того, что задано в условии задачи и что требуется определить, различают следующие два основных типа задач.

1. Исследуется движение тела в целом. В этих задачах вначале нужно получить законы (40)–(42) и, используя связь между ними, определить требуемую величину (см. примеры 17 и 18).

2. Требуется определить скорости и ускорения отдельных точек тела. Для решения задач этого типа вначале надо установить кинематические характеристики движения всего тела в целом, т.е. найти , и . После чего по формулам (43), (44), (45), (46) определить скорости и ускорения точек тела (см. пример 19).

Пример 17. Пропеллер самолета, делающий 1200 об / мин , после выключения двигателя останавливается через 8 с. Сколько оборотов сделал пропеллер за это время, если считать его вращение равнозамедленным?

Вначале получим законы вращения пропеллера (40), (41) и (42). По условию задачи пропеллер вращается равнозамедленно , из этого следует, что

.

, (47)

(48)

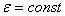
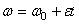
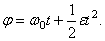
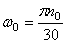
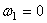
Начальной угловой скоростью при замедленном вращении будет та, которую пропеллер имел до выключения двигателя. Следовательно, . В момент остановки при t₁ = 8 сек. угловая скорость тела . Подставляя эти значения в уравнение (47), получим

Отсюда

Если обозначить число сделанных пропеллером за время t₁ оборотов через N₁, то угол поворота за то же время будет равен

.

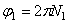
Подставляя найденные значения и в уравнение (48), получим

Отсюда оборотов.

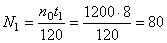
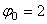
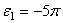
Пример 18. Найти закон вращения тела вокруг оси, если известны следующие данные: угловая скорость изменяется пропорционально t 2 , начальный угол поворота рад, для заданного момента времени t₁ = 3 с угловое ускорение 1/с 2 .

По условию задачи модуль угловой скорости изменяется пропорционально t 2 . Обозначая неизвестный коэффициент пропорциональности буквой k , имеем

. (49)

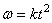
Найдем , беря производные по времени от обеих частей равенства (49),

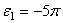
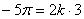
Определим коэффициент k из условия, что при t₁ = 3 сек. угловое ускорение 1/с 2 : или

Подставляя значение k в уравнение (49), получим

Учитывая, что 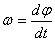, будем иметь

Умножая обе части этого уравнения на dt и интегрируя, находим

В начальный момент при t = 0, 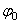= 2 рад, следовательно, c = 2.

Таким образом, 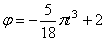радиан.

Пример 19. В период разгона ротор электродвигателя вращается по закону 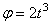, где t в сек, в рад.

Определить в конце 4-й секунды линейную скорость, вращательное, осестремительное и полное ускорения точки, лежащей на ободе ротора, если диаметр ротора D = 40 см .

По заданному уравнению вращения ротора находим его угловую скорость и угловое ускорение , .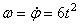

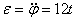
Подставляя значение t₁ = 4 сек в выражение для и , найдем

1/с,

1/с 2 .

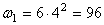
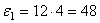
Определим модули линейной скорости, вращательного и осестремительного ускорений в этот же момент времени по формулам (43), (44) и (45)

Модуль полного ускорения точки обода ротора определим по формуле (46)

3. Определение скоростей и ускорений в случаях, когда вращающееся тело входит в состав различных механизмов

Рассмотрим механизмы с поступательным и вращательным движением звеньев. Решение задачи начинают с определения скоростей точек того звена, для которого движение задано. Затем рассматривают звено, которое присоединено к первому звену и т.д. В результате определяют скорости точек всех звеньев механизма. В такой же последовательности определяют и ускорения точек.

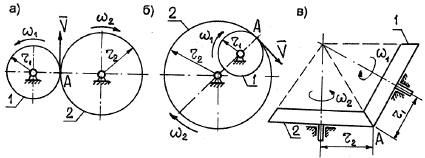
Передача вращения от одного вращающегося тела, называемого ведущим, к другому, называемому ведомым, может осуществляться при помощи фрикционной или зубчатой передачи (рис. 19).

Во фрикционной передаче вращение передается вследствие действия силы трения в месте контакта соприкасающихся колес, в зубчатой передаче – от зацепления зубьев. Оси вращения ведущего и ведомого колес могут быть параллельными (рис. 19, а, б) или пересекаться (рис. 19, в). В рассмотренных случаях линейные скорости точек А соприкасания колес одинаковы, их модули определяются так:

. (50)

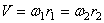
Отсюда 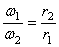. (51)

То есть угловые скорости колес фрикционной или зубчатой передачи обратно пропорциональны радиусам колес.

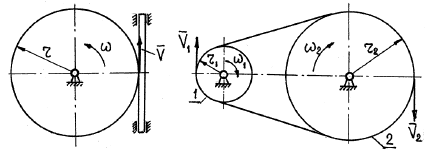
При преобразовании вращательного движения в поступательное (или наоборот) часто используют зацепление зубчатого колеса с зубчатой рейкой (рис. 20). Для этой передачи выполняется условие: .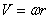

Кроме фрикционной и зубчатой передач, существует передача вращения при помощи гибкой связи (ремня, троса, цепи) (рис. 21).

Так как модули скоростей всех точек ремня одинаковы и ремень не скользит по поверхностям шкивов, то соотношения (50) и (51) относятся и к ременной передаче.

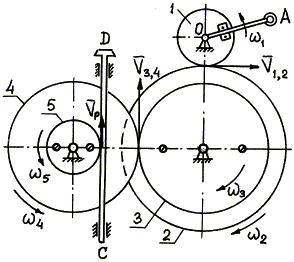
Пример 20. В механизме домкрата при вращении рукоятки ОА шестерни 1, 2, 3, 4, 5 приводят в движение зубчатую рейку ВС домкрата (рис. 22).

Определить скорость рейки, если рукоятка ОА делает 30 оборотов в минуту ( n = 30 об /мин). Числа зубцов шестерен: z₁ = 6, z₂ = 24, z₃ = 8, z₄ = 32; радиус пятой шестерни r₅ = 4 см .

Так как рукоятка ОА жестко соединена с шестерней 1, то последняя делает тоже 30 об /мин или

Модули скоростей точек соприкасания зубчатых колес 1 и 2 одинаковы для точек обоих колес и определяются по формуле (50)

Отсюда 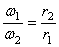(см. также (51)).

Так как числа зубьев пропорциональны радиусам колес, то .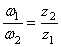

Отсюда

Шестерни 2 и 3 жестко соединены между собой, поэтому

Для находящихся в зацеплении колес 3 и 4 на основании (51) можно записать

Отсюда

Шестерни 4 и 5 жестко соединены между собой, поэтому

Модули скоростей точек соприкосновения зубчатой рейки ВС и шестерни 5 одинаковы, поэтому

или

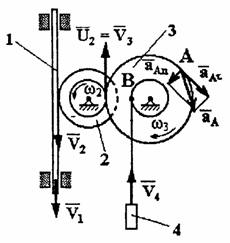
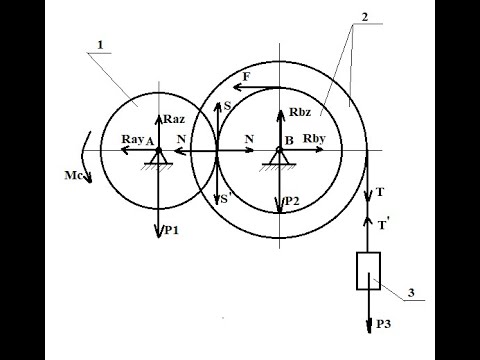
Пример 21. Рейка 1, ступенчатое колесо 2 с радиусами R ₂ и r ₂ и колесо 3 радиуса R ₃ , скрепленное с валом радиуса r₃, находятся в зацеплении; на вал намотана нить с грузом 4 на конце (рис.23). Рейка движется по закону

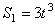
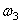
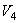
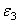
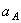
Дано: R ₂ =6 см, r₂=4 см, R₃=8 см, r₃=3 см, ( S — в сантиметрах, t — в секундах), А — точка обода колеса 3, t ₁ =3 с. Определить: , , , в момент времени t = t₁.

Указания. Пример 21 — на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что, когда два колеса находятся в зацеплении, скорость точки зацепления каждого колеса одна и та же, а когда два колеса связаны передачей, то скорости всех точек ремня и, следовательно, точек, лежащих на ободе каждого из этих колес, в данный момент времени численно одинаковы, при этом считается, что ремень по ободу колес не скользит.

Условимся обозначать скорости точек, лежащих на внешних ободах колес (радиуса R ₁ ), через V₁, а точек, лежащих на внутренних ободах (радиуса r ₁ ), через U₁.

1. Зная закон движения рейки 1, находим ее скорость:

. ( 52 )

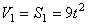
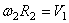
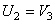
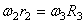
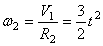
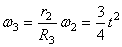
Так как рейка и колесо 2 находятся в зацеплении, то V ₂ = V₁ или . Но колеса 2 и 3 тоже находятся в зацеплении, следовательно, или . Из этих равенств находим:

, . (53)

Тогда для момента времени t₁ = 3 сек. получим 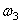= 6,75 с -1 .

2. Определяем V ₄ . Так как 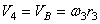, то при t₁=3 c ек . V ₄ = 20 ,25 см/с.

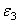
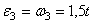
3. Определяем . Учитывая второе из равенств (53), получим .

Тогда при t₁ = 3 сек. 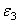= 4,5 с -2 .

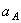
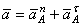
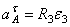
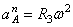
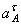
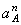
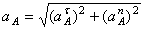
4. Определяем . Для точки А , где численно , . Тогда для момента времени t₁ = 3 сек. имеем = 36 см/с2, = 364,5 см/с2.

= 366,3 см/с 2 ,

Все скорости и ускорения точек, а также направления угловых скоростей показаны на рис.2.

Ответ: 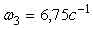, см/ с , , .

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Кинематика точки и твердого тела (стр. 4 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5

По заданному уравнению вращения тела φ = t2 – 3t определить угловую скорость, угловое ускорение и характер вращения тела в момент t1 = 1 с.

1. ω = 1 с–1; ε = – 2 с–2 — замедленное.

2. ω = – 1 с–1; ε = – 2 с–2 — ускоренное.

3. ω = 1 с–1; ε = + 2 с–2 — равноускоренное.

4. ω = – 1 с–1; ε = + 2 с–2 — равнозамедленное.

Основная задача кинематики твердого тела:

1) определить положение тела в выбранной системе отсчета;

2) вычислить кинематические характеристики тела;

3) определить положение тела в выбранной системе отсчета, кинематические характеристики всего тела, а затем каждой его точки.

Простейшими видами движения твердого тела являются:

2) плоскопараллельное движение.

Тема 5. ОПРЕДЕЛЕНИЕ ДВИЖЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ

ТВЕРДОГО ТЕЛА И ИХ КИНЕМАТИЧЕСКИХ ХАРАКТЕРИСТИК

Изучив движение всего тела в целом и установив кинематические характеристики его, перейдем к изучению движения и кинематических характеристик каждой точки тела.

Рассмотрим движение какой-либо точки М вращающегося тела (рис. 44). Эта точка при вращении тела будет описывать окружность в плоскости, перпендикулярной оси вращения, и с центром О, лежащим на оси вращения. Расстояние от точки до оси вращения называется радиусом вращения. Обозначим его через R (OM = R). Выберем за начало отсчета дуговых координат точку O1, лежащую в плоскости I, а за положительное направление — направление вращения тела. Тогда

S = = R φ.

Найдем скорость точки

vM = = R = R ω.

Называется эта скорость линейной скоростью точки. Изобразим траекторию точки М в плоскости нашего листа. Получим такое изображение (рис. 45), где вектор направлен по касательной к траектории точки М.

Вывод. Линейная скорость точки пропорциональна радиусу вращения и направлена перпендикулярно ему. Для различных точек тела при вращательном движении скорости будут различны. Распределение скоростей таких точек можно увидеть на рис. 46 (для точек прямой MM1).

Определим ускорение точки М (линейное). Так как точка М движется по кривой, то ускорение ее будет складываться из касательного и нормального:

Изобразим траекторию точки М и расставим эти векторы (рис. 47). Вектор āτ направлен, как и , перпендикулярно радиусу вращения, а ān — по радиусу к оси вращения. ā cоставляет с радиусом угол α, tg α = |aτ|/an. Найдем величину этих векторов (из кинематики точки):

an = v2/ρ; aτ = dv/dt; .

an = v2/R = R2ω2/R = R ω2; ;

tg α = |ε|/ω2;

. (14)

Вывод. Линейное ускорение точки пропорционально радиусу вращения и составляет с ним угол α, tg α = |ε|/ω2.

Для различных точек вращающегося тела ускорения различны. Распределение ускорений показано на рис. 48 (для точек прямой MM1).

Угловая скорость и угловое ускорение тела как векторные величины

Доказательство некоторых теорем кинематики и динамики, если рассматривать угловую скорость и угловое ускорение как векторные величины, можно упростить. Вектор (рис. 49), изображающий угловую скорость, строят на оси вращения, направляя его вдоль оси в ту сторону, чтобы, глядя с его конца, видеть вращение происходящим против часовой стрелки. Начало его можно поместить в любой точке оси, — вектор скользящий. Модуль || = |dφ/dt| = | | равен абсолютной величине угловой скорости.

Вектор = d/dt.

Если взять орт оси z — , то ω = φ и = (d/ dt) или = , т. е. вектор углового ускорения направлен, как и , по оси z и равен по модулю | |. Точку приложения можно поместить в любую точку оси вращения, — скользящий вектор.

Вектор может совпадать по направлению с , может не совпадать. Если вращение ускоренное, то оба вектора направлены в одну сторону (рис. 50), если замедленное — в разные (рис. 51).

Пользуясь векторными понятиями угловой скорости и углового ускорения, выразим линейную скорость и линейное ускорение в виде векторных произведений.

Выражение линейной скорости и ускорения в виде векторных

Пусть мы имеем тело, вращающееся около неподвижной оси. Изобразим его угловую скорость и угловое ускорение в виде векторов и . Начало их поместим в точку О оси вращения. Возьмем в теле любую точки М. Проведем из точки О радиус-вектор точки М — . Угол между осью z и обозначим через α. Покажем, что вектор линейной скорости точки М .

В этом нетрудно убедиться, вспомнив определение векторного произведения двух векторов. Векторное произведение двух векторов есть новый вектор, перпендикулярный плоскости, в которой лежат два данных вектора, и равен по модулю произведению их модулей на синус угла между ними. Вектор (рис. 52) перпендикулярен плоскости ΔOMO1 и равен ωr sin α = ωR (R = r sin α из ΔOMO1).

Вектор линейной скорости v = ω R, и направлен перпендикулярно R, т. е. плоскости ΔOMO1 в ту сторону, чтобы поворот и происходил против часовой стрелки. Следовательно, векторы и равны, что и требовалось доказать.

(15)

— основная формула кинематики или формула Эйлера.

Вектор линейного ускорения получим как производную от вектора скорости по времени:

ā = dv/dt = d()/dt = (d/dt)´ + ´ (d/dt) = =´ + ´,

так как d/dt = ; d/dt = .

Вектор ā равен сумме двух векторов. Покажем, что ´ — есть āτ, ´ — ān — векторы касательного и нормального ускорений. Вектор ´ равен по модулю εr sin α = εR и направлен перпендикулярно плоскости, в которой лежат и , т. е. плоскости ΔOMO1, следовательно, ´ есть вектор, перпендикулярный радиусу вращения и равный произведению углового ускорения на радиус вращения, т. е. этот вектор равен āτ.

Вектор ´ по модулю равен ωv sin β, нo β = 90° и ωv sin β = ωv = ω2R, так как v = ω R.

Направлен он перпендикулярно плоскости, в которой лежат и , т. е. по радиусу к центру (рис. 53).

Итак, ´ = ān; ´= āτ; ā = āτ + ān;

āτ = ´; (16)

ān = ´. (17)

Пример. На шкив радиусом R = 0,5 м навернут торс, к свободному концу которого подвешен груз А (рис. 54). Груз опускается из состояния покоя равноускоренно с ускорением aA = 2 м/с2 и приводит во вращение шкив. Найти закон вращательного движения шкива, угловую скорость, угловое ускорение его в произвольный момент времени t, а также скорость и ускорение āM точки М, лежащей на ободе шкива. Груз движется равноускоренно, значит, можно найти его скорость vA = aAt = 2t м/с. Скорость груза равна скорости точек обода, т. е. vM = vA = 2t, тогда ω = vM /R = 4t c–1, угловое ускорение ε = dω/dt = 4 c–1, т. е. ε = const и вращение шкива равноускоренное. ω0 = 0 и потому закон вращения:

Ускорение āМ = āτM + ānM, но aτM = R ε = 2 м/с, anM = R ω2 = 0,5∙16 t2 = 8 t2 м/с2, тогда = м/с2.

Рядовая зубчатая передача

Вращательное движение широко распространено в различных машинах и механизмах. Вращение может передаваться на расстояние посредством гибких связей (ременные передачи) или непосредственным соприкосновением (фрикционные или зубчатые передачи). В ременных и фрикционных передачах используются силы трения, а в зубчатых — механическое зацепление. В каждом из этих видов передач имеется ведущее звено, которое сообщает движение, и ведомые звенья, которые получают движение от ведущего звена. Рассмотрим рядовую зубчатую передачу или рядовое соединение зубчатых колес.

Соединение зубчатых колес, у которых все валы вращаются в неподвижных подшипниках, называется рядовым соединением или рядовой зубчатой передачей (рис. 55).

Расстояние между двумя соседними зубьями называют шагом зубчатой передачи h:

; ,

где R1, z1 — радиус и число зубьев I колеса; R2, z2 — радиус и число зубьев II колеса.

Рядовая передача характеризуется передаточным числом. Передаточное число i1,2 зубчатой передачи равно отношению угловой скорости ведущего колеса ω1 к угловой скорости ведомого ω2. i1,2 = ω1/ω2.

Передаточное число может быть выражено отношением радиусов колеса, т. к. vA = ω1 R1 и
vA = ω2 R2, тогда ω1 R1 = ω2 R2 или

, но и .

Если в зацеплении находится n колес, то передаточное число такой передачи равно произведению передаточных чисел сцепленных пар:

i1n = i12 i23 … i(n–1)n; или ,

где m — число внешних зацеплений.

При внутреннем зацеплении (рис. 56) передаточное число положительно, при внешнем — отрицательно.

Зубчатый редуктор состоит из трех зубчатых колес (рис. 57). Первое колесо имеет диаметр 0,2 м и делает 7 200 об/мин. Второе колесо — 4 000 об/мин, а третье — 600 об/мин. Определить диаметры второго и третьего колеса.

1. d2 = 0,36 м; d3 = 2,4 м.

2. d2 = 0,18 м; d3 = 1,2 м.

3. Нет верного ответа.

Колесо радиусом 0,8 м, вращающееся в период разгона равноускоренно из состояния покоя, совершило за некоторое время 750 оборотов. Определить время разгона, если скорости точек на ободе достигли при этом 200 м/с.

Колесо радиусом 0,5 м, вращаясь равноускоренно, имеет через 10 с угловую скорость n = 120 об/мин (n0 = 0). Определить ускорение точки А обода колеса в момент t = 1 мин.

3. аА = 2 880 м/с2.

№49

Рукоятка ОА (рис. 58) вращается по закону φ = 5t. Определить, за какое время груз поднимается на высоту 5 м, если r1 = 0,2 м; r2 = 0,3 м; r3 = 0,15 м.

Вращение тела вокруг неподвижной оси задано уравнением φ = 1,5t2 – 4t. Определить скорость и ускорение точки тела, отстоящей от оси вращения на 0,2 м в момент t1 = 2 с.

Чему равно линейное ускорение точки вращающегося тела?

3. .

Маховик радиусом R = 1,2 м вращается равномерно, делая n = 90 об/мин. Определить скорость и ускорение точки, лежащей на ободе маховика.

1. v = const = 3,6π м/с; a = 0.

2. v = const = 3,6π м/с; a = const = 10,8π2 м/с2.

3. v ≠ const; a = const = 10,8π2 м/с2; v = at = 10,8π2 м/с/

Груз B приводит во вращение вал радиусом r и сидящую на одной оси с валом шестерню 1 радиусом r1 (рис. 59). Движение груза начинается из состояния покоя и происходит с постоянным ускорением a. Определить закон вращения шестерни 2 радиусом r2.

1. .

2. .

3. .

Как распределятся ускорения точек вращающегося тела при его равномерном вращении (рис. 60–62)?

Диск вращается вокруг неподвижной оси в течение некоторого промежутка так, что ускорения всех точек составляют с их скоростями одинаковые углы, равные 45˚. Определить угловую скорость диска как функцию времени, если в момент t = 0 она была равна ω0.

ОТВЕТЫ И РЕШЕНИЯ

Способы задания движения точки

Движение точки при координатном способе задается ее координатами, которые выражаются функциями времени. В выбранной системе отсчета точка М будет иметь координаты

,

где φ = 2t. Подставив значение φ, получим

.

Ответ 2 задает движение этой точки естественным способом, ответ 3 — векторным. Следовательно, они здесь не являются верными.

При естественном способе движение точки задается дуговой координатой S = О1М, которая выражается функцией времени. В данной задаче известен угол φ = 2t, через него и выразим дугу О1М. S = R φ = 2tR; S = О1М = 2Rt — закон движения данной точки М.

Ответ 3 верен, 1 и 2 неверны, они задают движение векторным и координатным способами, а не естественным.

3. Неверно найдены уравнения движения точки Д. Их просто определить, если найти , тогда

, но .

1. Неверный. Вы перепутали название координатных осей.

2. Неверный. Ответ неполный. Вы не указали область изменения координат.

3. Неверный. Неверно указана область изменения координаты z. Так как z = t, а всегда t ≥ 0, то условие – ∞ ≤ z 0, то x и y должны быть больше нуля. Траектория — правая часть параболы. Верен ответ 2. Остальные неверны. Вы ошиблись в расчетах, проверьте их снова.

Чтобы задать движение точки естественным способом, нужно дуговую координату S = выразить функцией времени. Учитывая, что S = Rφ, имеем S = = 10t 4 = 40t (м).

Верен ответ 2. Ответ 1 задает движение координатным способом, ответ 3 — векторным. Они для данного случая неверны.

Чтобы найти уравнение движения ползунов А и В, нужно их координаты xA и yA выразить функциями времени: xA = ОА = 2l cos φ = 2l cos 3t (из ΔОАС), а yB = OB = 2l sin φ = 2l sin 3t (из ΔОАВ) (см. рис. 11).

Это и будут уравнения движения ползунов А и В.

Остальные ответы неверны. Ответ 1 — координаты перепутаны, а 2 и 3 будут верны только в момент, когда φ = 45˚.

Чтобы задать движение точки М координатным способом, нужно ее координаты выразить функциями времени. Это можно сделать, учитывая, что φ = 10 t.

Рассмотрим ΔОМК, ОК = xM = r cos φ = 4 cos 10t (м),

Это и будут уравнения движения точки М. Верен ответ 2. Ответы 1 и 3 неверны. Ответ 1 задает движение точки естественным способом, а 3 — векторным.

Верен ответ 3. Стержень движется так же, как точка А его. Ее закон движения будет и законом движения стержня. Найдем этот закон. Точка А движется только по оси x, и ее положение определяется одной координатой

x = OA = OC cos φ + = a cos kt + .

Ответ 2 определяет движение точки С. В ответе 1 sin и cos переставлены. Эти ответы неверны.

1. Неверно. Вы, видимо, находили ответ, используя неверную формулу

v = (S – S0)/t = (5 + 6t + t3 – 5)/t = 6 + t2 для v = const, затем = 9, 6 + t2 =9,

t = t1 = с; S1 =5 + 6 + 3 = (5 + 9) м.

Скорость равна производной по времени от дуговой координаты:

2. Неверно. Вы, видимо не знаете, чему равна скорость точки при естественном способе движения в данный момент времени: = , либо неверен был сам ход решения задачи. Либо вообще не знаете, как решать эту задачу. Надо было найти, используя приведенную выше формулу скорости точки, момент времени t1, когда скорость достигает 9 м/с, а затем для найденного момента дуговую координату: 6 + 3 t2 = 9, t1 = 1 с, St1 = 5 + 6 + 1 = 12 м.

3. Верно, St1 = 12 м.

4. Вы нашли путь, который прошла точка к моменту времени, когда скорость равна 9 м/с, П = |S – S0| = 7 м; но П ≠ S.

1. Неверно. Вы неверно определяете момент времени, соответствующий пройденному пути. Здесь надо было воспользоваться формулой пути П:

S1 = – 2 м — значение дуговой координаты в момент времени t1 = 4 c, в который скорость изменяет свой знак, а S2 = 0,5 м — значение дуговой координаты в тот момент времени (t1), когда точка пройдет путь, который задан. Положить П = 10,5 м, а не S =10,5 м. 10,5 = |– 2 – 6| + | S2+ 2|; S2 = 0,5 м.

t2 – 8t + 12 – 1 = 0; t2,3 = 4 ±= 4 ± c/

Видео:Вращательное движение твёрдого тела. Задачи 1, 2, 3Скачать

Вращения твердого тела вокруг неподвижной точки

Содержание:

Вращением твердого тела вокруг неподвижной оси называется такое движение твердого тела, при котором хотя бы две его точки остаются неподвижными. Прямая, проходящая через эти неподвижные точки называется осью вращения. Траекториями движения точек твердого тела являются окружности с радиусами равными расстояниям от заданных точек тела до оси вращения.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Видео:Вращение тела вокруг неподвижной осиСкачать

Вращения твердого тела вокруг неподвижной точки (сферическое движение)

Движение тела вокруг неподвижной точки (центра) называется сферическим движением. Сформулируем определение сферического движения.

Вращением твердого тела вокруг неподвижной точки называют такое движение, при котором одна точка тела остается все время неподвижной, а все остальные точки движутся по кругам, которые расположены на поверхностях сфер, описанных с неподвижной точки.

Одной из главных задач при изучении сферического движения является нахождение величин, характеризующих это движение: положение тела, угловые скорость и ускорение тела, вычисления скоростей и ускорений точек тела.

Рассмотрим движение тела вокруг неподвижного центра О (рис. 2.39). Выберем неподвижную систему отсчета Ox₁y₁z₁, относительно которой будем изучать движение тела, и подвижную — Oxyz, которую жестко свяжем с телом, что движется. Начало обеих систем координат расположим в неподвижном центре.

Для определения положения вращающегося тела относительно неподвижной системы координат Ox₁y₁z₁ необходимо задать относительно этой системы координат положения другой, подвижной системы координат Oxyz, скрепленной с движущимся телом. Для этого Эйлер предложил следующую теорему:

«Произвольное перемещение твердого тела вокруг неподвижной точки можно выполнить тремя последовательными поворотами тела вокруг трех осей, проходящих через неподвижную точку».

Согласно этой теореме положения тела, вращающегося вокруг неподвижной точки, определяется тремя углами. Линия ОК, вдоль которой пересекаются плоскости Oxy и Ox₁y₁ называется линией узлов. Тогда положения подвижных осей координат x, y, z (рис. 2.39) по отношению к неподвижной системе отсчета Ox₁y₁z₁ можно определить тремя углами:

,

,

.

Эти углы носят название углов Эйлера и имеют следующие наименования:

1. — угол прецессии, изменение которого означает вращение тела вокруг оси Oz₁, которая называется осью прецессии;

2. — угол нутации, изменение которого характеризует вращение тела вокруг линии узлов ОК, которая является осью нутации;

3. φ — угол собственного вращения, изменение которого означает вращение тела вокруг оси Oz, которая является осью собственного вращения.

Первый угол y, угол прецессии, который определяет положение линии узлов ОК относительно неподвижной координатной оси Ox₁, считается положительным, если он отсчитывается при повороте линии узлов ОК против часовой стрелки, если смотреть навстречу оси Oz₁.

Вторым углом Эйлера является угол нутации , угол между координатными плоскостями x₁Oy₁ и xOy, который можно измерять между перпендикулярами к указанным плоскостям — Oz₁ и Oz. Положительное направление угла — поворот против часовой стрелки оси Oz вокруг точки О, если смотреть навстречу линии узлов ОК. Угол отсчитывается от оси Oz₁.

Для полного определения положения данного тела относительно неподвижной системы Ox₁y₁z₁ необходимо задать угол между подвижной осью Ох и положительным направлением линии узлов ОК — угол собственного вращения φ. Этот угол считается положительным, если он меняется против часовой стрелки, смотря навстречу оси Oz.

При изменении угла φ тело вращается вокруг оси собственного вращения Oz, перпендикулярной плоскости, где расположены прямые ОК и O_x, образующих этот угол. Таким образом, угол φ определяет положение подвижной координатной оси Ox относительно линии узлов ОК.

Углы Эйлера широко применяются в теории гироскопа. Движение гироскопа, симметричного тела с неподвижной точкой на оси симметрии, которое очень быстро (30-40 тысяч об/мин.) вращается вокруг этой оси, можно представить составленным из трех движений, которые определяются углами , , φ . Изменение углов и имеет скорость на 1-2 порядка ниже, чем угла собственного вращения φ.

При вращении тела вокруг неподвижной точки в общем случае изменяются все три угла Эйлера: , , φ. Эти углы являются независимыми параметрами, которые определяют положение тела при сферическом движении относительно неподвижной системы координат. Задание трех углов Эйлера, как функции времени, являются необходимыми и достаточными условиями для полного описания сферического движения.

Следовательно, для определения положения тела с одной неподвижной точкой в ​​любой момент времени необходимо задать углы Эйлера как однозначные и непрерывные функции времени:

,

,

.

Уравнение является кинематическими уравнениями вращения твердого тела вокруг неподвижной точки. Если эти уравнения заданы, то в любой момент времени может быть определено положение твердого тела относительно неподвижной системы координат.

Действительно, отложим сначала в плоскости x₁Oy₁ от оси Ox₁ угол прецессии y против часовой стрелки, если он положительный, и определим положение линии узлов ОК. Далее отложим угол q от оси Oz₁, плоскость которого перпендикулярна линии узлов ОК, и определим положение оси z собственного вращения. И наконец, отложим в плоскости xOy угол φ от линии узлов против часовой стрелки, если он положительный, и определим положение оси Ox. Положение тела определено однозначно.

Теорема Эйлера – Даламбера

Произвольное элементарное перемещение тела, имеющего одну неподвижную точку, может осуществляться по одному элементарному повороту вокруг некоторой специально выбранной мгновенной оси вращения, проходящей через эту неподвижную точку.

Предположим, что положение тела, которое вращается вокруг точки О, определяется углами , , φ (как это показано на рис. 2.39).

Тогда его перемещения за элементарный промежуток времени можно представить как совокупность поворотов на углы d, d, dφ, вокруг оси Oz₁, линии узлов ОК и оси Oz соответственно. Прибавляясь, эти три поворота создадут одно действительное элементарное перемещение тела.

Сначала рассмотрим, каким будет результат сложения поворотов вокруг осей Oz и Oz₁, (рис. 2.40). При повороте на угол dφ любая точка тела, лежащего в плоскости Ozz₁ (внутри угла zOz₁), получит элементарное перемещение, которое перпендикулярно этой плоскости и численно равна , — расстояние от точки до оси Oz. Одновременно, при повороте вокруг оси Oz₁ та же точка получит обратное перемещение, которое численно равна .

Внутри угла обязательно найдется такая точка В, для которой = . Это означает, что перемещение этой точки равно нулю, и точка B будет неподвижной. Таким образом, имеем две неподвижные точки O и В, следовательно, неподвижную ось ОВ, вокруг которой происходит то самое элементарное вращение, которое составляет сумму вращений вокруг осей Oz и Oz₁.

Если теперь рассматривать вращения вокруг оси ОВ и линии узлов ОК, после аналогичных соображений придем к выводу, что элементарные повороты вокруг осей ОВ и ОК эквивалентны элементарному повороту вокруг некоторой оси ОР, проходящей через точку О.

Таким образом, ось ОР, элементарным поворотом вокруг которой тело перемещается из данного положения в соседнее, бесконечно близкое данному называется мгновенной осью вращения.

Следует заметить, что от неподвижной мгновенная ось вращения отличается тем, что ее положение меняется как в отношении системы отсчета Ox₁y₁z₁, так и в отношении подвижной системы координат Oxyz. Каждое последующее вращение происходит вокруг своей мгновенной оси вращения, которая, безусловно, всегда пересекает неподвижную точку О.

То есть, движение твердого тела вокруг неподвижной точки состоит из серии последовательных элементарных поворотов вокруг мгновенных осей вращения, которые пересекают неподвижную точку.

Геометрическое место мгновенных осей вращения относительно неподвижной системы отсчета называется недвижимым аксоидом. Неподвижный аксоид является конической поверхностью с вершиной в неподвижной точке тела, потому что все мгновенные оси пересекают неподвижную точку.

Геометрическое место мгновенных осей во вращающемся теле называют подвижным аксоидом, который также является конической поверхностью. Для каждого движения твердого тела вокруг неподвижной точки имеем пару аксоидов. Таким образом, во вреся сферического движения подвижной аксоид катится по неподвижному без скольжения, поскольку общая образующая этих аксоидов в каждый момент времени служит мгновенной осью, вокруг которой вращается тело, поэтому все точки оси неподвижные. Если подвижный аксоид катится без скольжения по неподвижному аксоиду, то происходит движение тела вокруг неподвижной точки.

Кинематические характеристики движения тела вокруг неподвижной точки

Угловая скорость:

Сделаем сначала определения угловой скорости тела, вращающегося вокруг неподвижной точки.

Угловая скорость, с которой происходит элементарный поворот тела вокруг мгновенной оси вращения, называется угловой скоростью тела в данный момент времени или мгновенной угловой скоростью тела.

Согласно этому определению, если тело вернется вокруг мгновенной оси на некоторое бесконечно малый угол dφ, то мгновенной угловой скоростью будет:

.

Угловую скорость можно изобразить в виде вектора , направленного вдоль мгновенной оси ОР (рис. 2.41).

Если учесть, что положение мгновенной оси ОР непрерывно меняется, то вектор угловой скорости будет меняться в течении времени как по модулю, так и по направлению, а конец вектора будет описывать некоторую произвольную кривую AB, которая является годографом вектора . На рис. 2.41 показаны различные положения мгновенной оси вращения OP, OP₁, OP₂ и соответственно расположенные на них векторы угловой скорости , и .

Угловое ускорение:

Второй кинематической характеристикой тела, вращающегося вокруг неподвижной точки является угловое ускорение.

Угловое ускорение тела в данный момент времени, или мгновенное угловое ускорение , которое характеризует изменение в течении времени угловой скорости по модулю и по направлению, является векторной величиной и численно равна:

.

Для нахождения расположения вектора углового ускорения можно использовать такую ​​аналогию. Как известно, вектор скорости произвольной точки равен производной от радиус-вектора этой точки по времени t и направлен вдоль касательной к траектории движения точки. В этом случае траектория точки является годографом концов радиус-векторов .

По аналогии с этим, вектор углового ускорения направлен по касательной к кривой AB в соответствующей точке. То есть, угловое ускорение можно считать, как скорость движения конца вектора .

Таким образом, вектор мгновенного углового ускорения имеет направление производной по времени от вектора мгновенной угловой скорости , он параллельный касательной к годографу векторной функции (t). Изображать угловое ускорение необходимо вектором, параллельный касательно к годографу векторов угловой скорости в данной точке, но приложенный к неподвижной точке O (рис. 2.40).

Скорости и ускорения точек тела в сферическом движении

Векторная формула Эйлера (2.54), полученная для вращательного движения тела вокруг неподвижной оси, справедлива и для сферического движения тела.

В сферическом движении в каждый момент времени тело вращается вокруг мгновенной оси OP, которая пересекает неподвижную точку O, с угловой скоростью , вектор которой расположен на мгновенной оси. Точки тела, которые принадлежат мгновенной оси OP, имеют скорости , равны нулю, как и в случае неподвижной оси вращения.

Следовательно, скорость произвольной точки М тела (рис. 2.42) определяется как векторное произведение и . А именно:

,

где — радиус-вектор точки M относительно неподвижной точки О.

Модуль скорости при этом будет равен:

,

где h — кратчайшее расстояние точки к мгновенной оси OP.

Таким образом, скорости точек тела в сферическом движении пропорциональны расстояниям от этих точек к мгновенной оси. Направление вектора скорости перпендикулярно плоскости, в которой расположены векторы и , то есть расстоянию h и направлен в сторону вращения.

Как известно, скорость точки является первой производной от радиус-вектора этой точки по времени (2.4):

.

В то же время, по векторной формуле (2.54) скорость равна , откуда:

Длина радиус-вектора , как расстояние между двумя точками твердого тела, является постоянной величиной при движении этого тела. Следовательно, уравнение (2.77) можно рассматривать как формулу для вычисления производной по времени от вектора, модуль которого устойчивый, а изменение его происходит только вследствие вращения с угловой скоростью вместе с телом вокруг неподвижной точки.

Если жестко скрепить подвижную систему координат Oxyz с телом, вращающимся вокруг неподвижной точки с угловой скоростью , так для единичных векторов , , , направленных по этим осям, модули которых постоянные, на основании (2.77) имеем:

,

,

.

Выражения называют формулами Пуассона.

Для определения ускорения точки тела, которое осуществляет сферическое движение, возьмем производную по скалярному аргументу t (время) от векторной функции скорости :

.

,

.

тогда окончательно имеем:

В отличии от вышеупомянутой формулы, здесь и — угловые скорость и ускорение вокруг мгновенных осей, первое слагаемое — вращательное ускорение:

,

второе слагаемое — осевое ускорение:

.

Движение свободного твердого тела

Рассмотрим наиболее общий случай движения твердого тела — свободное движение тела, когда оно может как угодно перемешиваться относительно неподвижной системы отсчета Oxyz (рис. 2.43).

Как известно из аналитической геометрии, положения твердого тела в пространстве можно определить тремя точками, которые не расположены на одной прямой и неизменно связаны с телом.

На девять координат этих точек наложено три ограничения, которые выражают неизменность расстояний между точками, потому что они принадлежат твердому телу. Итак, независимых параметров или степеней свободы тела будет шесть.

Смотря с другой стороны, при определении положения твердого тела можно задать три координаты одной его точки, например, точки A, которую назовем полюсом с координатами , , , и выбрать еще три параметра, характеризующих вращения тела вокруг полюса. Остальные параметры могут быть углами Эйлера , , φ (на рис. 2.43 не показаны). Совокупность шести скалярных функций времени, которые однозначно определяют положение свободного твердого тела в любой момент времени, является законом его движения:

,

,

,

,

,

.

Три первые уравнения определяют движение полюса и вместе с ним поступательное движение твердого тела. Последние три уравнения определяют движение тела относительно системы координат (то есть относительно точки A, как неподвижной).

Таким образом, с геометрической точки зрения элементарное перемещение свободного тела состоит из поступательного перемещения вместе с полюсом, при котором полюс переходит в соседнее положение , и с некоторого перемещения по отношению к осям .

Последнее перемещения по теореме Эйлера-Даламбера является поворотом вокруг мгновенной оси вращения , которая проходит через точку A.

Поскольку движением тела является совокупность элементарных перемещений, то можно его обозначить следующим образом:

«Свободное движение тела в общем случае состоит из поступательного движения, при котором все точки тела движутся как произвольно выбранный полюс A со скоростью полюса , и ряда элементарных поворотов с угловой скоростью ω вокруг мгновенных осей вращения, которые проходят через полюс» (рис. 2.44).

Свободно движутся брошенный камень, снаряд, неуправляемая ракета тому подобное.

Основными кинематическими характеристиками движения является скорость и ускорение полюса, которые определяют скорость и ускорение поступательной части движения, а также угловая скорость ω и угловое ускорение ε вращения вокруг полюса. Значения величин этих характеристик можно определить по уравнениям.

В отдельном случае движение свободного тела может быть плоскопараллельным. Тогда вектор угловой скорости будет всегда перпендикулярен плоскости движения. При этом, как в общем случае, так и в отдельном, вращающаяся часть движения, как и значение угловой скорости ω, от выбора полюса не зависит.

Определим скорости и ускорения точек свободного тела.

Как и в случае плоскопараллельного движения, можно предположить, что скорость и ускорение точки свободного тела состоит геометрически со скорости ускорения векторов полюса и относительной скорости (ускорение) точки вокруг полюса (последние получает точка M при движении вместе с телом вокруг полюса A)

,

,

где ; ; — радиус-вектор точки M относительно полюса A; — скорость точки M относительно полюса A; — ускорение точки M относительно полюса A; ε — угловое ускорение тела.

Услуги по теоретической механике:

Учебные лекции:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

🎥 Видео

Основное уравнение динамики вращательного движения. 10 класс.Скачать

Урок 100. Задачи на вращение твердого тела (ч.1)Скачать

Урок 96. Простейшие задачи на вращение твердого телаСкачать

Урок 93. Основное уравнение динамики вращательного движенияСкачать

Консультация к устному экзамену. Механика. Часть 4: "Вращение твердых тел"Скачать

Лекция №8 "Вращение твердых тел" (Попов П.В.)Скачать

§2.2. Вращение твердого тела вокруг неподвижной оси.Скачать

Вращательное движение твердого телаСкачать

Кинематика вращательного движения. ТермехСкачать

Поступательное и вращательное движение твердого тела. Уравнение движения.Скачать

Поступательное и вращательное движенияСкачать

Лекция №9 "Общее вращение твердого тела. Гироскопы" (Попов П.В.)Скачать

Физика 10 класс (Урок№5 - Поступательное движение. Вращательное движение твердого тела.)Скачать

Кинематика: Поступательное и вращательное движение твёрдого тела. Центр онлайн-обучения «Фоксфорд»Скачать

Якута А. А. - Механика - Теорема Эйлера. Момент инерции. Тензор инерцииСкачать