Глава 16. Динамика твердого тела.

16.1. Дифференциальные уравнения движения твердого тела вокруг неподвидеой оси.

16.1.1. По заданному уравнению вращения φ = 5 t 2 — 2 пластинки, осе­вой момент инерции которой I_z = 0,125 кг • м 2 , определить главный момент внешних сил, действующих на пластинку. (Ответ 1,25)

16.1.2. По заданному уравнению вращения φ = 2(t 2 + 1) наклонного стержня с осевым моментом инерции I_z = 0,05 кг • м 2 опреде­лить главный момент внешних сил, действую­щих на тело. (Ответ 0,2)

16.1.3. Диск вращается вокруг оси O_z по закону φ = t 3 . Определить модуль момента пары сил, приложенной к диску, в момент времени t = 1 с, если момент инерции диска относитель­но оси вращения равен 2 кг • м 2 . (Ответ 12)

16.1.4. По заданному уравнению вращения φ = 3t 2 — t стержня с осевым моментом инер­ции I_z = 1 /₆ кг • м 2 определить главный мо­мент внешних сил, действующих на стержень. (Ответ 1)

16.1.5. По заданному уравнению вращения φ = t 3 — 5t 2 однородного цилиндра радиуса R = 1,41 м, массой m = 60 кг определить главный момент внешних сил, действующих на тело, в момент времени t = 2 с. (Ответ 119)

16.1.6. Конус, масса которого m = 10 кг, а радиус основания R = 1 м, вращается вокруг оси симметрии по закону φ = 4sin 2t. Определить главный момент приложенных к конусу внеш­них сил относительно оси вращения в момент времени t = π/4 с, если момент инерции конуса I_z = 0,3 mR 2 . (Ответ -48)

16.1.7. По заданному уравнению вращения φ = 2sin(πt/2) однородной прямоугольной пли­ты с моментом инерции относительно оси вра­щения I_z = 10 кг • м 2 определить главный мо­мент внешних сил, действующих на тело, в момент времени t = 1 с. (Ответ -49,3)

16.1.8. Вал двигателя вращается с угловой скоростью ω = 90 е -20t + 85 (1 + е -20t ). Определить главный момент внешних сил, действу­ющих на вал, в момент времени t = 0,1 с, если его момент инерции относительно оси вращения равен 1 кг • м 2 . (Ответ -13,5)

16.1.9. Диск вращается вокруг центральной оси с угловым ускорением ϵ = 4 рад/с 2 под дейст­вием пары сил с моментом M₁ и момента сил сопротивления М₂ = 6 Н • м. Определить модуль момента M₁ пары сил, если момент инерции диска относительно оси вращения равен 6 кг • м 2 . (Ответ 30)

16.1.10. Однородный стержень, масса которого m = 2 кг и длина AВ = 1 м, вращается вокруг оси О_z под действием пары сил с моментом М₁ и момента сил сопротивления М₂ = 12 Н м по закону φ = 3t 2 . Определить модуль момента M₁ приложенной пары сил в момент времени t = 1 с. (Ответ 16)

16.1.11. Определить угловое ускорение диска ради­уса r = 0,3 м массой m = 50 кг, если натяже­ния ведущей и ведомой ветвей ремня соответ­ственно равны T₁ = 2Т₂ = 100 Н. Радиус инер­ции диска относительно оси вращения равен 0,2 м. (Ответ 7,5)

16.1.12. Определить угловое ускорение однород­ного тонкого диска радиуса R = 0,6 м, массой 4 кг, вращающегося вокруг вертикальной оси A_z под действием момента M_z = 1,8 Н • м. (Ответ 5)

16.1.13. Определить угловое ускорение однород­ного стержня массой m = 4 кг и длиной l = 1 м, вращающегося вокруг оси O_z, если к стержню приложен вращающий момент M_z = 3Н • м. (Ответ 9)

16.1.14. Определить угловое ускорение вращения вокруг оси O_z однородного стержня массой m = 3 кг и длиной l = 1 м. На стержень дейст­вует пара сил с моментом М₂ = 2 Н • м. (Ответ 2)

16.1.15. Однородный стержень, масса которого m = 8 кг и длина AВ = 1,5 м, вращается вокруг оси O_z под действием пары сил с мо­ментом М = 12 sin (3 π/4)t. Определить угловое ускорение стержня в момент времени t = 2 /₃ c. (Ответ 2)

16.1.16. При разгоне на ротор двигателя действует пара сил с моментом М = 100(1 — ω/200). Определить максимальное значение углового ускорения ротора, если его момент инерции относительно оси вращения равен 2 кг • м 2 . (Ответ 50)

16.1.17. На этапе разгона на ротор двигателя действует пара сил с момен­том М = 40(1 — t/10). Определить максимальное значение углового ускорения ротора, если его момент инерции относительно оси враще­ния равен 0,5 кг • м 2 . (Ответ 80)

16.1.18. Однородный диск радиуса r = 0,1 м под действием силы тяжести начинает вращение в вертикальной плоскости вокруг горизон­тальной оси O_z из положения, когда его радиус ОС горизонтален. В этот момент времени опре­делить угловое ускорение диска. (Ответ 65,4)

Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Кинематика точки и твердого тела (стр. 4 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5

По заданному уравнению вращения тела φ = t2 – 3t определить угловую скорость, угловое ускорение и характер вращения тела в момент t1 = 1 с.

1. ω = 1 с–1; ε = – 2 с–2 — замедленное.

2. ω = – 1 с–1; ε = – 2 с–2 — ускоренное.

3. ω = 1 с–1; ε = + 2 с–2 — равноускоренное.

4. ω = – 1 с–1; ε = + 2 с–2 — равнозамедленное.

Основная задача кинематики твердого тела:

1) определить положение тела в выбранной системе отсчета;

2) вычислить кинематические характеристики тела;

3) определить положение тела в выбранной системе отсчета, кинематические характеристики всего тела, а затем каждой его точки.

Простейшими видами движения твердого тела являются:

2) плоскопараллельное движение.

Тема 5. ОПРЕДЕЛЕНИЕ ДВИЖЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ

ТВЕРДОГО ТЕЛА И ИХ КИНЕМАТИЧЕСКИХ ХАРАКТЕРИСТИК

Изучив движение всего тела в целом и установив кинематические характеристики его, перейдем к изучению движения и кинематических характеристик каждой точки тела.

Рассмотрим движение какой-либо точки М вращающегося тела (рис. 44). Эта точка при вращении тела будет описывать окружность в плоскости, перпендикулярной оси вращения, и с центром О, лежащим на оси вращения. Расстояние от точки до оси вращения называется радиусом вращения. Обозначим его через R (OM = R). Выберем за начало отсчета дуговых координат точку O1, лежащую в плоскости I, а за положительное направление — направление вращения тела. Тогда

S = = R φ.

Найдем скорость точки

vM = = R = R ω.

Называется эта скорость линейной скоростью точки. Изобразим траекторию точки М в плоскости нашего листа. Получим такое изображение (рис. 45), где вектор направлен по касательной к траектории точки М.

Вывод. Линейная скорость точки пропорциональна радиусу вращения и направлена перпендикулярно ему. Для различных точек тела при вращательном движении скорости будут различны. Распределение скоростей таких точек можно увидеть на рис. 46 (для точек прямой MM1).

Определим ускорение точки М (линейное). Так как точка М движется по кривой, то ускорение ее будет складываться из касательного и нормального:

Изобразим траекторию точки М и расставим эти векторы (рис. 47). Вектор āτ направлен, как и , перпендикулярно радиусу вращения, а ān — по радиусу к оси вращения. ā cоставляет с радиусом угол α, tg α = |aτ|/an. Найдем величину этих векторов (из кинематики точки):

an = v2/ρ; aτ = dv/dt; .

an = v2/R = R2ω2/R = R ω2; ;

tg α = |ε|/ω2;

. (14)

Вывод. Линейное ускорение точки пропорционально радиусу вращения и составляет с ним угол α, tg α = |ε|/ω2.

Для различных точек вращающегося тела ускорения различны. Распределение ускорений показано на рис. 48 (для точек прямой MM1).

Угловая скорость и угловое ускорение тела как векторные величины

Доказательство некоторых теорем кинематики и динамики, если рассматривать угловую скорость и угловое ускорение как векторные величины, можно упростить. Вектор (рис. 49), изображающий угловую скорость, строят на оси вращения, направляя его вдоль оси в ту сторону, чтобы, глядя с его конца, видеть вращение происходящим против часовой стрелки. Начало его можно поместить в любой точке оси, — вектор скользящий. Модуль || = |dφ/dt| = | | равен абсолютной величине угловой скорости.

Вектор = d/dt.

Если взять орт оси z — , то ω = φ и = (d/ dt) или = , т. е. вектор углового ускорения направлен, как и , по оси z и равен по модулю | |. Точку приложения можно поместить в любую точку оси вращения, — скользящий вектор.

Вектор может совпадать по направлению с , может не совпадать. Если вращение ускоренное, то оба вектора направлены в одну сторону (рис. 50), если замедленное — в разные (рис. 51).

Пользуясь векторными понятиями угловой скорости и углового ускорения, выразим линейную скорость и линейное ускорение в виде векторных произведений.

Выражение линейной скорости и ускорения в виде векторных

Пусть мы имеем тело, вращающееся около неподвижной оси. Изобразим его угловую скорость и угловое ускорение в виде векторов и . Начало их поместим в точку О оси вращения. Возьмем в теле любую точки М. Проведем из точки О радиус-вектор точки М — . Угол между осью z и обозначим через α. Покажем, что вектор линейной скорости точки М .

В этом нетрудно убедиться, вспомнив определение векторного произведения двух векторов. Векторное произведение двух векторов есть новый вектор, перпендикулярный плоскости, в которой лежат два данных вектора, и равен по модулю произведению их модулей на синус угла между ними. Вектор (рис. 52) перпендикулярен плоскости ΔOMO1 и равен ωr sin α = ωR (R = r sin α из ΔOMO1).

Вектор линейной скорости v = ω R, и направлен перпендикулярно R, т. е. плоскости ΔOMO1 в ту сторону, чтобы поворот и происходил против часовой стрелки. Следовательно, векторы и равны, что и требовалось доказать.

(15)

— основная формула кинематики или формула Эйлера.

Вектор линейного ускорения получим как производную от вектора скорости по времени:

ā = dv/dt = d()/dt = (d/dt)´ + ´ (d/dt) = =´ + ´,

так как d/dt = ; d/dt = .

Вектор ā равен сумме двух векторов. Покажем, что ´ — есть āτ, ´ — ān — векторы касательного и нормального ускорений. Вектор ´ равен по модулю εr sin α = εR и направлен перпендикулярно плоскости, в которой лежат и , т. е. плоскости ΔOMO1, следовательно, ´ есть вектор, перпендикулярный радиусу вращения и равный произведению углового ускорения на радиус вращения, т. е. этот вектор равен āτ.

Вектор ´ по модулю равен ωv sin β, нo β = 90° и ωv sin β = ωv = ω2R, так как v = ω R.

Направлен он перпендикулярно плоскости, в которой лежат и , т. е. по радиусу к центру (рис. 53).

Итак, ´ = ān; ´= āτ; ā = āτ + ān;

āτ = ´; (16)

ān = ´. (17)

Пример. На шкив радиусом R = 0,5 м навернут торс, к свободному концу которого подвешен груз А (рис. 54). Груз опускается из состояния покоя равноускоренно с ускорением aA = 2 м/с2 и приводит во вращение шкив. Найти закон вращательного движения шкива, угловую скорость, угловое ускорение его в произвольный момент времени t, а также скорость и ускорение āM точки М, лежащей на ободе шкива. Груз движется равноускоренно, значит, можно найти его скорость vA = aAt = 2t м/с. Скорость груза равна скорости точек обода, т. е. vM = vA = 2t, тогда ω = vM /R = 4t c–1, угловое ускорение ε = dω/dt = 4 c–1, т. е. ε = const и вращение шкива равноускоренное. ω0 = 0 и потому закон вращения:

Ускорение āМ = āτM + ānM, но aτM = R ε = 2 м/с, anM = R ω2 = 0,5∙16 t2 = 8 t2 м/с2, тогда = м/с2.

Рядовая зубчатая передача

Вращательное движение широко распространено в различных машинах и механизмах. Вращение может передаваться на расстояние посредством гибких связей (ременные передачи) или непосредственным соприкосновением (фрикционные или зубчатые передачи). В ременных и фрикционных передачах используются силы трения, а в зубчатых — механическое зацепление. В каждом из этих видов передач имеется ведущее звено, которое сообщает движение, и ведомые звенья, которые получают движение от ведущего звена. Рассмотрим рядовую зубчатую передачу или рядовое соединение зубчатых колес.

Соединение зубчатых колес, у которых все валы вращаются в неподвижных подшипниках, называется рядовым соединением или рядовой зубчатой передачей (рис. 55).

Расстояние между двумя соседними зубьями называют шагом зубчатой передачи h:

; ,

где R1, z1 — радиус и число зубьев I колеса; R2, z2 — радиус и число зубьев II колеса.

Рядовая передача характеризуется передаточным числом. Передаточное число i1,2 зубчатой передачи равно отношению угловой скорости ведущего колеса ω1 к угловой скорости ведомого ω2. i1,2 = ω1/ω2.

Передаточное число может быть выражено отношением радиусов колеса, т. к. vA = ω1 R1 и
vA = ω2 R2, тогда ω1 R1 = ω2 R2 или

, но и .

Если в зацеплении находится n колес, то передаточное число такой передачи равно произведению передаточных чисел сцепленных пар:

i1n = i12 i23 … i(n–1)n; или ,

где m — число внешних зацеплений.

При внутреннем зацеплении (рис. 56) передаточное число положительно, при внешнем — отрицательно.

Зубчатый редуктор состоит из трех зубчатых колес (рис. 57). Первое колесо имеет диаметр 0,2 м и делает 7 200 об/мин. Второе колесо — 4 000 об/мин, а третье — 600 об/мин. Определить диаметры второго и третьего колеса.

1. d2 = 0,36 м; d3 = 2,4 м.

2. d2 = 0,18 м; d3 = 1,2 м.

3. Нет верного ответа.

Колесо радиусом 0,8 м, вращающееся в период разгона равноускоренно из состояния покоя, совершило за некоторое время 750 оборотов. Определить время разгона, если скорости точек на ободе достигли при этом 200 м/с.

Колесо радиусом 0,5 м, вращаясь равноускоренно, имеет через 10 с угловую скорость n = 120 об/мин (n0 = 0). Определить ускорение точки А обода колеса в момент t = 1 мин.

3. аА = 2 880 м/с2.

№49

Рукоятка ОА (рис. 58) вращается по закону φ = 5t. Определить, за какое время груз поднимается на высоту 5 м, если r1 = 0,2 м; r2 = 0,3 м; r3 = 0,15 м.

Вращение тела вокруг неподвижной оси задано уравнением φ = 1,5t2 – 4t. Определить скорость и ускорение точки тела, отстоящей от оси вращения на 0,2 м в момент t1 = 2 с.

Чему равно линейное ускорение точки вращающегося тела?

3. .

Маховик радиусом R = 1,2 м вращается равномерно, делая n = 90 об/мин. Определить скорость и ускорение точки, лежащей на ободе маховика.

1. v = const = 3,6π м/с; a = 0.

2. v = const = 3,6π м/с; a = const = 10,8π2 м/с2.

3. v ≠ const; a = const = 10,8π2 м/с2; v = at = 10,8π2 м/с/

Груз B приводит во вращение вал радиусом r и сидящую на одной оси с валом шестерню 1 радиусом r1 (рис. 59). Движение груза начинается из состояния покоя и происходит с постоянным ускорением a. Определить закон вращения шестерни 2 радиусом r2.

1. .

2. .

3. .

Как распределятся ускорения точек вращающегося тела при его равномерном вращении (рис. 60–62)?

Диск вращается вокруг неподвижной оси в течение некоторого промежутка так, что ускорения всех точек составляют с их скоростями одинаковые углы, равные 45˚. Определить угловую скорость диска как функцию времени, если в момент t = 0 она была равна ω0.

ОТВЕТЫ И РЕШЕНИЯ

Способы задания движения точки

Движение точки при координатном способе задается ее координатами, которые выражаются функциями времени. В выбранной системе отсчета точка М будет иметь координаты

,

где φ = 2t. Подставив значение φ, получим

.

Ответ 2 задает движение этой точки естественным способом, ответ 3 — векторным. Следовательно, они здесь не являются верными.

При естественном способе движение точки задается дуговой координатой S = О1М, которая выражается функцией времени. В данной задаче известен угол φ = 2t, через него и выразим дугу О1М. S = R φ = 2tR; S = О1М = 2Rt — закон движения данной точки М.

Ответ 3 верен, 1 и 2 неверны, они задают движение векторным и координатным способами, а не естественным.

3. Неверно найдены уравнения движения точки Д. Их просто определить, если найти , тогда

, но .

1. Неверный. Вы перепутали название координатных осей.

2. Неверный. Ответ неполный. Вы не указали область изменения координат.

3. Неверный. Неверно указана область изменения координаты z. Так как z = t, а всегда t ≥ 0, то условие – ∞ ≤ z 0, то x и y должны быть больше нуля. Траектория — правая часть параболы. Верен ответ 2. Остальные неверны. Вы ошиблись в расчетах, проверьте их снова.

Чтобы задать движение точки естественным способом, нужно дуговую координату S = выразить функцией времени. Учитывая, что S = Rφ, имеем S = = 10t 4 = 40t (м).

Верен ответ 2. Ответ 1 задает движение координатным способом, ответ 3 — векторным. Они для данного случая неверны.

Чтобы найти уравнение движения ползунов А и В, нужно их координаты xA и yA выразить функциями времени: xA = ОА = 2l cos φ = 2l cos 3t (из ΔОАС), а yB = OB = 2l sin φ = 2l sin 3t (из ΔОАВ) (см. рис. 11).

Это и будут уравнения движения ползунов А и В.

Остальные ответы неверны. Ответ 1 — координаты перепутаны, а 2 и 3 будут верны только в момент, когда φ = 45˚.

Чтобы задать движение точки М координатным способом, нужно ее координаты выразить функциями времени. Это можно сделать, учитывая, что φ = 10 t.

Рассмотрим ΔОМК, ОК = xM = r cos φ = 4 cos 10t (м),

Это и будут уравнения движения точки М. Верен ответ 2. Ответы 1 и 3 неверны. Ответ 1 задает движение точки естественным способом, а 3 — векторным.

Верен ответ 3. Стержень движется так же, как точка А его. Ее закон движения будет и законом движения стержня. Найдем этот закон. Точка А движется только по оси x, и ее положение определяется одной координатой

x = OA = OC cos φ + = a cos kt + .

Ответ 2 определяет движение точки С. В ответе 1 sin и cos переставлены. Эти ответы неверны.

1. Неверно. Вы, видимо, находили ответ, используя неверную формулу

v = (S – S0)/t = (5 + 6t + t3 – 5)/t = 6 + t2 для v = const, затем = 9, 6 + t2 =9,

t = t1 = с; S1 =5 + 6 + 3 = (5 + 9) м.

Скорость равна производной по времени от дуговой координаты:

2. Неверно. Вы, видимо не знаете, чему равна скорость точки при естественном способе движения в данный момент времени: = , либо неверен был сам ход решения задачи. Либо вообще не знаете, как решать эту задачу. Надо было найти, используя приведенную выше формулу скорости точки, момент времени t1, когда скорость достигает 9 м/с, а затем для найденного момента дуговую координату: 6 + 3 t2 = 9, t1 = 1 с, St1 = 5 + 6 + 1 = 12 м.

3. Верно, St1 = 12 м.

4. Вы нашли путь, который прошла точка к моменту времени, когда скорость равна 9 м/с, П = |S – S0| = 7 м; но П ≠ S.

1. Неверно. Вы неверно определяете момент времени, соответствующий пройденному пути. Здесь надо было воспользоваться формулой пути П:

S1 = – 2 м — значение дуговой координаты в момент времени t1 = 4 c, в который скорость изменяет свой знак, а S2 = 0,5 м — значение дуговой координаты в тот момент времени (t1), когда точка пройдет путь, который задан. Положить П = 10,5 м, а не S =10,5 м. 10,5 = |– 2 – 6| + | S2+ 2|; S2 = 0,5 м.

t2 – 8t + 12 – 1 = 0; t2,3 = 4 ±= 4 ± c/

Теоретическая механика:
Вращательное движение твердого тела

Смотрите также решения задач по теме «Вращательное движение» в онлайн решебниках Яблонского, Мещерского, Чертова (с примерами и методичкой для заочников), Иродова и Савельева.

При поступательном движении тела (§ 60 в учебнике Е. М. Никитина) все его точки движутся по одинаковым траекториям и в каждый данный момент они имеют равные скорости и равные ускорения.

Поэтому поступательное движение тела задают движением какой-либо одной точки, обычно движением центра тяжести.

Рассматривая в какой-либо задаче движение автомобиля (задача 147) или тепловоза (задача 141), фактически рассматриваем движение их центров тяжести.

Вращательное движение тела (Е. М. Никитин, § 61) нельзя отождествить с движением какой-либо одной его точки. Ось любого вращающегося тела (маховика дизеля, ротора электродвигателя, шпинделя станка, лопастей вентилятора и т. п.) в процессе движения занимает в пространстве относительно окружающих неподвижных тел одно и то же место.

Движение материальной точки или поступательное движение тела характеризуют в зависимости от времени линейные величины s (путь, расстояние), v (скорость) и а (ускорение) с его составляющими a_t и a_n.

Вращательное движение тела в зависимости от времени t характеризуют угловые величины : φ (угол поворота в радианах), ω (угловая скорость в рад/сек) и ε (угловое ускорение в рад/сек 2 ).

Закон вращательного движения тела выражается уравнением
φ = f (t).

Угловая скорость – величина, характеризующая быстроту вращения тела, определяется в общем случае как производная угла поворота по времени
ω = dφ/dt = f’ (t).

Угловое ускорение – величина, характеризующая быстроту изменения угловой скорости, определяется как производная угловой скорости
ε = dω/dt = f» (t).

Приступая к решению задач на вращательное движение тела, необходимо иметь в виду, что в технических расчетах и задачах, как правило, угловое перемещение выражается не в радианах φ, а в оборотах φ_об.

Поэтому необходимо уметь переходить от числа оборотов к радианному измерению углового перемещения и наоборот.

Так как один полный оборот соответствует 2π рад, то
φ = 2πφ_об и φ_об = φ/(2π).

Угловая скорость в технических расчетах очень часто измеряется в оборотах, произведенных в одну минуту (об/мин), поэтому необходимо отчетливо уяснить, что ω рад/сек и n об/мин выражают одно и то же понятие – скорость вращения тела (угловую скорость), но в различных единицах – в рад/сек или в об/мин.

Переход от одних единиц угловой скорости к другим производится по формулам
ω = πn/30 и n = 30ω/π.

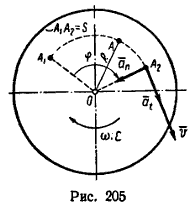
При вращательном движении тела все его точки движутся по окружностям, центры которых расположены на одной неподвижной прямой (ось вращающегося тела). Очень важно при решении задач, приведенных в этой главе, ясно представлять зависимость между угловыми величинами φ, ω и ε, характеризующими вращательное движение тела, и линейными величинами s, v, a_t и a_n, характеризующими движение различных точек этого тела (рис 205).

Если R – расстояние от геометрической оси вращающегося тела до какой-либо точки А (на рис. 205 R=OA), то зависимость между φ – углом поворота тела и s – расстоянием, пройденным точкой тела за то же время, выражается так:
s = φR.

Зависимость между угловой скоростью тела и скоростью точки в каждый данный момент выражается равенством
v = ωR.

Касательное ускорение точки зависит от углового ускорения и определяется формулой
a_t = εR.

Нормальное ускорение точки зависит от угловой скорости тела и определяется зависимостью
a_n = ω 2 R.

При решении задачи, приведенной в этой главе, необходимо ясно понимать, что вращением называется движение твердого тела, а не точки. Отдельно взятая материальная точка не вращается, а движется по окружности – совершает криволинейное движение.

Видео:Поверхности второго порядкаСкачать

§ 33. Равномерное вращательное движение

Если угловая скорость ω=const, то вращательное движение называется равномерным.

Уравнение равномерного вращения имеет вид
φ = φ₀ + ωt.

В частном случае, когда начальный угол поворота φ₀=0,
φ = ωt.

Угловую скорость равномерно вращающегося тела
ω = φ/t
можно выразить и так:
ω = 2π/T,
где T – период вращения тела; φ=2π – угол поворота за один период.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

§ 34. Равнопеременное вращательное движение

Вращательное движение с переменной угловой скоростью называется неравномерным (см. ниже § 35). Если же угловое ускорение ε=const, то вращательное движение называется равнопеременным . Таким образом, равнопеременное вращение тела – частный случай неравномерного вращательного движения.

Уравнение равнопеременного вращения
(1) φ = φ₀ + ω₀t + εt 2 /2
и уравнение, выражающее угловую скорость тела в любой момент времени,
(2) ω = ω₀ + εt
представляют совокупность основных формул вращательного равнопеременного движения тела.

В эти формулы входят всего шесть величин: три постоянных для данной задачи φ₀, ω₀ и ε и три переменных φ, ω и t. Следовательно, в условии каждой задачи на равнопеременное вращение должно содержаться не менее четырех заданных величин.

Для удобства решения некоторых задач из уравнений (1) и (2) можно получить еще две вспомогательные формулы.

Исключим из (1) и (2) угловое ускорение ε:
(3) φ = φ₀ + (ω + ω₀)t/2.

Исключим из (1) и (2) время t:
(4) φ = φ₀ + (ω 2 — ω₀ 2 )/(2ε).

В частном случае равноускоренного вращения, начавшегося из состояния покоя, φ₀=0 и ω₀=0. Поэтому приведенные выше основные и вспомогательные формулы принимают такой вид:
(5) φ = εt 2 /2;
(6) ω = εt;
(7) φ = ωt/2;
(8) φ = ω 2 /(2ε).

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

§ 35. Неравномерное вращательное движение

Рассмотрим пример решения задачи, в которой задано неравномерное вращательное движение тела.

💥 Видео

Вращательное движение. 10 класс.Скачать

§64 Поверхности вращенияСкачать

Вращательное движение твёрдого тела. Задачи 1, 2, 3Скачать

Цилиндрические поверхностиСкачать

Момент силы относительно точки и осиСкачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Первая основная задача динамики. Задачи 1, 2, 3, 4Скачать

Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Уравнение плоскости через 2 точки параллельно векторуСкачать

14. Что такое параметрически заданная функция, производная параметрически заданной функции.Скачать

Кинематика вращательного движения. ТермехСкачать

Урок 103. Задачи на вращение твердого тела (ч.2)Скачать