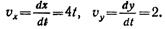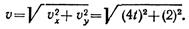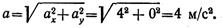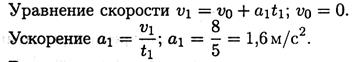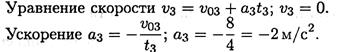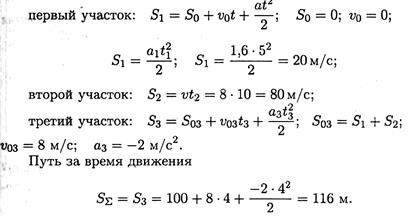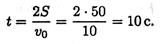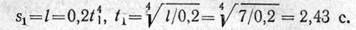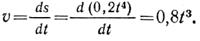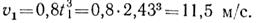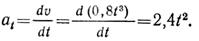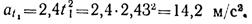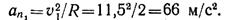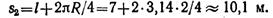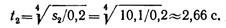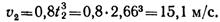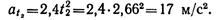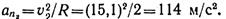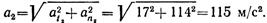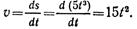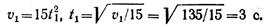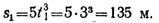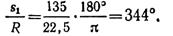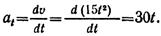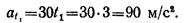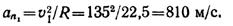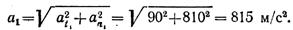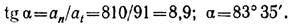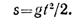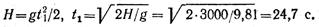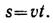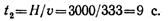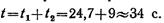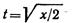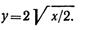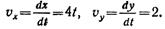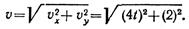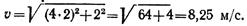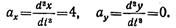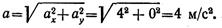По заданному уравнению движения точки s 22t 4t постройте графики скорости и касательного ускорения

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Решение. Для определения траектории точки нужно из уравнений движения исключить параметр t — время

Для определения траектории точки нужно из уравнений движения исключить параметр t — время.

Выразим t через х из первого уравнения:

и подставим это значение во второе уравнение:

Траекторией точки является парабола, симметричная относительно оси х.

Чтобы найти скорость точки, нужно определить ее составляющие по координатным осям

Находим скорость точки

При t = 2 с получаем

Находим составляющие ускорения точки

Контрольные вопросы и задания

1. Запишите формулу ускорения при прямолинейном движении.

2. Запишите формулу ускорения (полного) при криволинейном движении.

3. Тело скатывается по желобу (рис. 10.7). Какие параметры движения меняются при переходе через точку В и почему?

4. Параметры движения не меняются.

4. По заданному уравнению движения точки S = 25 + 1,5t + 6t 2 определите вид движения и без расчетов, используя законы движе­ния точки, ответьте, чему равны начальная скорость и ускорение.

5. По заданному уравнению движения точки S = 22t — 4t 2 постройте графики скорости и касательного ускорения.

6. По графику скоростей точки определите путь, пройденный за время движения (рис. 10.8).

7. Точка движется по дуге. Охарактеризуй движение точки (рис. 10.9).

Видео:Решение графических задач на равномерное движениеСкачать

Примеры решения задач

Иметь представление о скоростях средней и истинной, об ускорении при прямолинейном и криволинейном движениях, о различных видах движения точки.

Знать формулы (без вывода) и графики равномерного и равнопеременного движений точки.

Уметь определять параметры движения точки по заданному закону движения, строить и читать кинематические графики.

кинетических параметров движений

Равномерное движение — это движение с постоянной скоростью:

Конспекты и лекции по сопромату Курсовые и лабораторные

Для прямолинейного равномерного движения (рис. 10.1а)

Полное ускорение движения точки равно нулю: а = 0.

При криволинейном равномерном движении (рис. 10.1б).

Полное ускорение равно нормальному ускорению: а = ап.

Уравнение (закон) движения точки при равномерном движении можно получить, проделав ряд несложных операций.

Так как v = const, закон равномерного движения в общем виде является уравнением прямой: S = So+vt, где Sо — путь, пройденный до начала отсчета.

Равнопеременное движение — это движение с постоянным касательным ускорением:

Для прямолинейного равнопеременного движения

a = at = const.

Полное ускорение равно касательному ускорению. Криволинейное равнопеременное движение (рис. 10.2):

an ≠ 0; at = const ≠ 0.

Учитывая, что ; аt = const и сделав ряд преобразований:

получим значение скорости при равнопеременном движении

После интегрирования будем иметь закон равнопеременного движения в общем виде, представляющий уравнение параболы:

где v0 — начальная скорость движения;

So — путь, пройденный до начала отсчета;

at — постоянное касательное ускорение.

При неравномерном движении численные значения скорости и ускорения меняются.

Уравнение неравномерного движения в общем виде представляет собой уравнение третьей S = f(t3) и выше степени.

Контрольные вопросы и задания

1. Запишите формулу ускорения при прямолинейном движении.

2.Запишите формулу ускорения (полного) при криволинейном
движении.

По заданному уравнению движения точки S = 22t + 4t2 постройте графики скорости и касательного ускорения.

Видео:Траектория и уравнения движения точки. Задача 1Скачать

По заданному уравнению движения точки s 22t 4t постройте графики скорости и касательного ускорения

Задачи по физике — это просто!

Не забываем, что решать задачи надо всегда в системе СИ!

А теперь к задачам!

Элементарные задачи из курса школьной физики по кинематике.

Задача на составление описания движения и составление уравнения движения по заданному графику движения

Дано: график движения тела

Найти:
1. составить описание движения
2. составить уравнение движения тела.

Проекцию вектора скорости определяем по графику, выбрав любой удобный для рассмотрения отрезок времени.
Здесь удобно взять t=4c

Составляем уравнение движения тела:

Записываем формулу уравнения прямолинейного равномерного движения.

Подставляем в нее найденный коэффициент V_x (не забываем о минусе!).
Начальная координата тела (X_о) соответствует началу графика, тогда X_о=3

Составляем описание движения тела:

Желательно сделать чертеж, это поможет не ошибиться!
Не забываем, что все физические величины имеют единицы измерения, их необходимо указывать!

Тело движется прямолинейно и равномерно из начальной точки X_о=3м со скоростью 0,75 м/с противоположно направлению оси X.

Задача на определение места и времени встречи двух движущихся тел (при прямолинейном равномерном движении)

Движение тел задано уравнениями движения для каждого тела.

Дано:
1. уравнение движения первого тела
2. уравнение движения второго тела

Найти:
1. координату места встречи
2. момент время (после начала движения), когда произойдет встреча тел

По заданным уравнениям движения строим графики движения для каждого тела в одной системе координат.

Точка пересечения двух графиков движения определяет:

1. на оси t — время встречи ( через сколько времени после начала движения произойдет встреча)
2. на оси X — координату места встречи (относительно начала координат)

В результате:

Два тела встретятся в точке с координатой -1,75 м через 1,25 секунд после начала движения.

Для проверки полученных графическим способом ответов можно решить систему уравнений из двух заданных
уравнений движения:

Для тех, кто почему-то забыл, как построить график прямолинейного равномерного движения:

График движения — это линейная зависимость ( прямая), строится по двум точкам.
Выбираем два любых удобных для простоты расчета значения t₁ и t₂.
Для этих значений t подсчитываем соответствующие значения координат X₁ и X₂.
Откладываем 2 точки с координатами (t₁, X₁) и (t₂, X₂) и соединяем их прямой — график готов!

Задачи на составление описания движения тела и построение графиков движения по заданному уравнению прямолинейного равномерного движения

Задача 1

Дано: уравнение движения тела

Найти:
1. составить описание движения
2. построить график движения

Заданное уравнение сравниваем с формулой и определяем коэффициенты.
Не забываем делать чертеж, чтобы еще раз обратить внимание на направление вектора скорости.

Задача 2

Дано: уравнение движения тела

Найти:
1. составить описание движения
2. построить график движения

Задача 3

Дано: уравнение движения тела

Найти:
1. составить описание движения
2. построить график движения

Задача 4

Дано: уравнение движения тела

Найти:
1. составить описание движения
2. построить график движения

Тело находится в состоянии покоя в точке с координатой X=4м (состояние покоя — это частный случай движения, когда скорость тела равна нулю).

Задача 5

Дано:
начальная координата движущейся точки xo=-3 м
проекция вектора скорости Vx=-2 м/с

Найти:
1. записать уравнение движения
2. построить график движения
3. показать на чертеже векторы скорости и перемещения
4. найти координату точки через 10 секунд после начала движения

Видео:Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

Примеры решения задач

Пример 1. По заданному закону движения S =10 + 20t — 5t 2 ([S] = м; [t] = с) определить вид движения, начальную скорость и касательное ускорение точки, время до остановки.

(Рекомендуется обойтись без расчетов, использовать метод срав­нения заданного уравнения с уравнениями различных видов движе­ний в общем виде.)

Решение

1. Вид движения: равнопеременное

2. При сравнении уравнений очевидно, что

• начальный путь, пройденный до начала отсчета – 10 м;
• начальная скорость 20 м/с;
• постоянное касательное ускорение a_t/2 = 5 м/с ; a_t= — 10 м/с .
• ускорение отрицательное, следовательно, движение замедлен­ное (равнозамедленное), ускорение направлено в сторону, противо­положную направлению скорости движения.

3. Можно определить время, при котором скорость точки будет равна нулю:

v = S’ = 20 — 2 • 5t; v = 20 – 10t = 0; t = 20/10 = 2 c.

Примечание. Если при равнопеременном движении скорость растет, значит, ускорение — положительная величина, гра­фик пути — вогнутая парабола. При торможении скорость падает, ускорение (замедление) — отрицательная величина, график пути — выпуклая парабола (рис. 10.4).

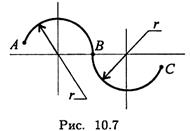
Пример 2. Точка движется по желобу из точки А в точку D (рис. 10.5).

Как изменятся касательное и нормальное ускорения при прохождении точки через В и С?

Скорость движения считать постоянной. Радиус участка АВ = 10 м, радиус участка ВС= 5 м.

Решение

1. Рассмотрим участок АВ. Касательное ускорение равно нулю (v = const).

Нормальное ускорение (а_п = v 2 /r) при переходе через точку В уве­личивается в 2 раза, оно меняет направление, т. к. центр дуги АВ не совпадает с центром дуги ВС.

2. На участке ВС:

— касательное ускорение равно нулю: a_t = 0;

— нормальное ускорение при переходе через точку С меняется: до точки С движение вращательное, после точки С движение стано­вится прямолинейным, нормальное напряжение на прямолинейном участке равно нулю.

3. На участке CD полное ускорение равно нулю.

Пример 3. По заданному графику скорости найти путь, прой­денный за время движения (рис. 10.6).

Решение

1. По графику следует рассмотреть три участка движения. Первый участок — разгон из состояния покоя (равноускоренное движение).

Второй участок — равномерное движение: v = 8 м/с; a₂ = 0.

Третий участок — торможение до остановки (равнозамедленное движение).

2. Путь, пройденный за время движения, будет равен:

Пример 4. Тело, имевшее начальную скорость 36 км/ч, про­шло 50 м до остановки. Считая движение равнозамедленным, опре­делить время торможения.

Решение

1. Записываем уравнение скорости для равнозамедленного дви­жения:

Определяем начальную скорость в м/с: v_о = 36*1000/3600 = 10 м/с.

Выразим ускорение (замедление) из уравнения скорости: a = — v₀/t

2. Записываем уравнение пути: S = v_ot/2 + at 2 /2. После подстановки получим: S = v_ot/2

3. Определяем время до полной остановки (время торможения):

Пример 5. Точка движется прямолинейно согласно уравнению s = 20t – 5t 2 (s — м, t — с). Построить графики расстояний, скорости и ускорения для первых 4 с движения. Определить путь, пройденный точкой за 4 с, и описать движение точки.

Решение

1. Точка движется прямолинейно по уравнению s = 20t – 5t 2 следовательно, скорость точки u = ds/d/t = 20 — 10t и ускорение a = a_t = dv/dt = —10 м/с 2 . Значит, движение точки равнопеременное (a = a_t = —10 м/c 2 = const) с начальной скоростью v₀ = 20 м/с.

2. Составим зависимость числовых значений s и v для первых 4 с движения

3. По приведенным числовым значениям построим графики расстояний (рис. а), скорости (рис. б) и ускорения (рис. в), выбрав мас­штабы для изображения по осям ординат расстояний s, скорости v и ускорения а, а также одинаковый для всех графиков масштаб времени по оси абсцисс. Напри­мер, если расстояние s = 5 м изображать на графике длиной отрезка l_s = 10 мм, то 5м = μ_s*10мм, где коэффициент пропорциональности μ_s и есть масштаб по оси Os : μ_s = 5/10 = 0,5 м/мм (0,5 м в 1 мм); если модуль скорости v = 10 м/с изобра­жать на графике длиной l_v =10 мм, то 10 м/c = μ_v * 10 мм и масштаб по оси Ov μ_v = 1 м/(с-мм) (1 м/с в 1 мм); если модуль ускорения а = 10 м/с 2 изображать отрезком l_a = 10 мм, то, аналогично предыдущему, масштаб по оси Оа μ_a = 1 м/(с 2 -мм) (1 м/с 2 в 1 мм); и наконец, изображая промежуток време­ни Δt = 1 с отрезком μ_t = 10 мм, получим на всех графиках масштаб по осям Ot μ_t = 0,1 с/мм (0,1 с в 1 мм).

4. Из рассмотрения графиков следует, что в течение времени от 0 до 2 с точка движется равнозамедленно (скорость v и ускорение в течение этого промежутка времени имеют разные знаки, значит, их векторы направлены в противоположные стороны); в период времени от 2 до 4 с точка движется равноускоренно (скорость v и ускорение имеют одинаковые знаки, т. е. их векторы направлены в одну сто­рону).

За 4 с точка прошла путь s_o_₄ = 40 м. На­чав движение со скоростью v₀ = 20 м/с, точка по прямой прошла 20 м, а затем вернулась в исходное положение, имея ту же скорость, но направленную в противоположную сторону.

Если условно принять ускорение свободно­го падения g = 10 мс 2 и пренебречь сопротивле­нием воздуха, то можно сказать, что графики описывают движение точки, брошенной верти­кально вверх со скоростью а₀ = 20 м/с.

Пример 6. Точка движется по траектории, изображенной на рис. 1.44, а, согласно уравнению s = 0,2t 4 (s — в метрах, t — в секундах). Определить скорость и ускорение точки в положениях 1 и 2.

Решение

Время, необходимое для перемещения точки из положения 0 (начала отсчета) в положение 1, опреде­лим из уравнения движения, подставив частные значения расстояния и времени:

Уравнение изменения скорости

Скорость точки в положении 1

Уравнение изменения касательного ускорения

Касательное ускорение точ­ки в положении 1

Нормальное ускорение точки на прямолинейном участке траектории равно нулю. Ско­рость и ускорение точки в конце этого участка траекто­рии показаны на рис.1.44, б.

Определим скорость и уско­рение точки в начале криво­линейного участка траектории. Очевидно, что v₁ = 11,5 м/с, а_t1 = 14,2 м/с 2 .

Нормальное ускорение точки в начале криволинейного участка

Скорость и ускорение в начале криволинейного участ­ка показаны на рис. 1.44, в (векторы a_t1 и a_a1 изобра­жены без соблюдения масштаба).

Положение 2 движущейся точки определяется прой­денным путем, состоящим из прямолинейного участка 0 — 1 и дуги окружности 1 — 2, соответствующей цент­ральному углу 90°:

Время, необходимое для перемещения точки из поло­жения 0 в положение2,

Скорость точки в положении 2

Касательное ускорение точки в положении 2

Нормальное ускорение точки в положении 2

Ускорение точки в положении 2

Скорость и ускорения точки в положении 2 показаны на рис. 1.44, в (векторы at„ и а_Пг изображены без соблюде­ния масштаба).

Пример 7. Точка движется по заданной траекто­рии (рис. 1.45, а) согласно уравнению s = 5t 3 (s — в мет­рах, t — в секундах). Определить ускорение точки и угол α между ускорением и скоростью в момент t₁, когда скорость точки v₁ = 135 м/с.

Решение

Уравнение изменения скорости

Время t₁ определим из уравнения изменения скорости, подставив частные значения скорости и времени:

Определим положение точки на траектории в момент 3 с:

Дуга окружности длиной 135 м соответствует цент­ральному углу

Уравнение изменения касательного ускорения

Касательное ускорение точки в момент t_t

Нормальное ускорение точки в момент t_t

Ускорение точки в момент t_x

Скорость и ускорение точки в момент времени t₁ по­казаны на рис. 1.45, б.

Как видно из рис. 1.45, б

Пример 8. В шахту глубиной H = 3000 м с по­верхности земли без начальной скорости брошен предмет. Определить, через сколько секунд звук, возникающий в момент удара предмета о дно шахты, достигнет поверх­ности земли. Скорость звука 333 м/с.

Решение

Уравнение движения свободно падающего тела

Время, необходимое для перемещения предмета от поверхности земли до дна шахты, определим из уравне­ния движения:

Звук распространялся с постоянной скоростью 333 м/с. Уравнение распространения звука

Время достижения звуком поверхности земли

Тогда время с момента начала движения предмета до момента достижения звуком поверхности земли

Пример 9. По заданным уравнениям движения точки x = 2t 2 , y = 2t (x и у — в метрах, t — в секундах) найти уравнение траектории, а также скорость и уско­рение точки в момент времени t = 2 с.

Решение

Для определения траектории точки нужно из уравнений движения исключить параметр t — время.

Выразим t через х из первого уравнения:

и подставим это значение во второе уравнение:

Траекторией точки является парабола, симметричная относительно оси х.

Чтобы найти скорость точки, нужно определить ее составляющие по координатным осям

Находим скорость точки

При t = 2 с получаем

Находим составляющие ускорения точки

Контрольные вопросы и задания

1. Запишите формулу ускорения при прямолинейном движении.

2. Запишите формулу ускорения (полного) при криволинейном движении.

3. Тело скатывается по желобу (рис. 10.7). Какие параметры движения меняются при переходе через точку В и почему?

4. Параметры движения не меняются.

4. По заданному уравнению движения точки S = 25 + 1,5t + 6t 2 определите вид движения и без расчетов, используя законы движе­ния точки, ответьте, чему равны начальная скорость и ускорение.

5. По заданному уравнению движения точки S = 22t — 4t 2 постройте графики скорости и касательного ускорения.

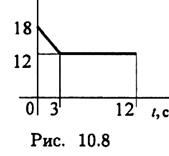
6. По графику скоростей точки определите путь, пройденный за время движения (рис. 10.8).

7. Точка движется по дуге. Охарактеризуй движение точки (рис. 10.9).

8. Ответьте на вопросы тестового задания.

Темы 1.7, 1.8. Кинематика. Кинематика точки

.

ЛЕКЦИЯ 11

Дата добавления: 2017-09-01 ; просмотров: 10662 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

🎬 Видео

Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать

Физика - уравнения равноускоренного движенияСкачать

К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать

Скорость и ускорение точки в полярных координатахСкачать

Урок 15. Решение задач на графики движенияСкачать

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Кинематика точки Задание К1Скачать

Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Кинематика точки. Три способа задания движения. Скорость, ускорениеСкачать

Урок 22 (осн). Подготовка к КР по теме "Скорость"Скачать

ЕГЭ по математике. Профильный уровень. Задание 7. Закон движения. ПроизводнаяСкачать

Графики зависимости кинематических величин от времени при равномерном и равноускоренном движенииСкачать

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Равноускоренное движение. Вывод формулСкачать

Способы описания движения. Траектория. Путь. ПеремещениеСкачать

Математический анализ, 5 урок, Непрерывность функцииСкачать