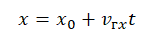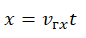По уравнению зависимости координаты от времени x t 90 sin 4 пt определить

Физика | 10 — 11 классы

Х = 3, 5sin(4πt + π / 3) — зависимость координаты тела, совершающего гармонические колебания, от времени.

Определить амплитуду, период и частоту колебаний.

v = 1 / T = 1 / 0, 5 = 2 Гц.

Видео:Физика: зависимость координаты тела от времениСкачать

3. По графику гармонических колебаний определите амплитуду, период и частоту колебаний?

3. По графику гармонических колебаний определите амплитуду, период и частоту колебаний.

Видео:РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ физика 9 ПерышкинСкачать

На рис?

Изображен график зависимости координаты тела, совершающего гармонические колебания , от времени .

Чему равны период и амплитуда этих колебаний ?

Видео:Физика - уравнения равноускоренного движенияСкачать

На рисунке изображен график зависимости координаты маятника от времени?

На рисунке изображен график зависимости координаты маятника от времени.

Определите по графику амплитуду, период и частоту колебаний маятника.

Видео:РЕАКЦИИ ИОННОГО ОБМЕНА, ИОННОЕ УРАВНЕНИЕ - Урок Химия 9 класс / Подготовка к ЕГЭ по ХимииСкачать

По графику колебаний определите амплитуду, период и частоту колебаний?

По графику колебаний определите амплитуду, период и частоту колебаний.

Видео:ВСЕ НОМЕРА 4 - ЕГЭ ПО ФИЗИКЕ I Банк задач EXAMhack I Физика ОГЭ ЕГЭ 2024I Эмиль Исмаилов I Global_EEСкачать

По графику гармонических колебаний определите амплитуду период и частоту колебаний?

По графику гармонических колебаний определите амплитуду период и частоту колебаний.

Видео:Решение задач на термохимические уравнения. 8 класс.Скачать

По графику гармонических колебаний определите амплитуду , период и частоту колебаний?

По графику гармонических колебаний определите амплитуду , период и частоту колебаний.

Видео:ВСЕ НОМЕРА 5 - ЕГЭ ПО ФИЗИКЕ I Банк задач EXAMhack I Физика ОГЭ ЕГЭ 2024I Эмиль Исмаилов I Global_EEСкачать

На рисунке график гармонических колебаний?

На рисунке график гармонических колебаний.

Найдите амплитуду, период и частоту колебаний.

Видео:Прямолинейное равноускоренное движение. Ускорение | Физика 9 класс #5 | ИнфоурокСкачать

Гармоническое колебание задано уравнением 2sin10Пtгармоническое колебание задано уравнением 2sin10Пt?

Гармоническое колебание задано уравнением 2sin10Пtгармоническое колебание задано уравнением 2sin10Пt.

Найти амплитуду, период и частоту колебаний.

Составить уравнение зависимости скорости от времени.

Видео:Урок 34. Свободное падение. Ускорение свободного паденияСкачать

Уравнение гармонических колебаний имеет вид х = 15 cos 10πt?

Уравнение гармонических колебаний имеет вид х = 15 cos 10πt.

Определите период колебаний, амплитуду и частоту.

Видео:Урок 329. Задачи на гармонические колебания - 1Скачать

По графику гармонических колебаний определить амплитуду , частоту и период колебаний , записать уравнение зависимости координаты х от времени t?

По графику гармонических колебаний определить амплитуду , частоту и период колебаний , записать уравнение зависимости координаты х от времени t.

На этой странице сайта, в категории Физика размещен ответ на вопрос Х = 3, 5sin(4πt + π / 3) — зависимость координаты тела, совершающего гармонические колебания, от времени?. По уровню сложности вопрос рассчитан на учащихся 10 — 11 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

S₁ = s₂ = s, тогда весь путь 2 * s t₁ = s / v₁ — время подъема в гору t₂ = s / v₂ — время спуска с горы t = t₁ + t₂ = s / v₁ + s / v₂ = s * (v₁ + v₂) / (v₁ * v₂) — общее время движения = 2 * s / t = 2 * s * (v₁ * v₂) / s * (v₁ + v₂) = 2 * v₁ * v₂ / (..

1) Проекция вектора мгновенной скорости на ось ОХ. Зависимость мгновенного значения пространственной координаты от временной координаты. 2) Проекция вектора мгновенной скорости на ось ОХ без начальной скорости. Зависимость мгновенного значения про..

2 с 3 с 4 с 5 а лови ответ.

M = 400 кг L = 9 * 10 ^ 5 Дж / кг Q = ? = = = Q = m * L = 400 * 9 * 10 ^ 5 = 3. 6 * 10 ^ 8 Дж (360 МДж) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =.

20мин = 1200сек. S = Vt = 15 * 1200 = 18000метров = 18км.

15 умножается на 20 минут равно 300 метров.

Лист с листом не входят в одно целое, а мокрые листы становятся одним целым из за того что вода начинает соприкасаться друг с другом.

U — внутренняя энергия. U = (Eк + Eп) молекул тела. Если повысить температуру тела, то его внутренняя энергия увеличится, т. К. увеличится средняя скорость движения молекул. Таким образом, увеличивается кинетическая энергия молекул тела. Способы..

Видео:Задачи на скорость реакции в зависимости от концентрации реагентовСкачать

Уравнение координаты при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Уравнение координаты — зависимость координаты тела от времени:

Уравнение координаты при равноускоренном прямолинейном движении:

x₀ — координата тела в начальный момент времени, v_0x —проекция начальной скорости на ось ОХ, a_x —проекция ускорения на ось ОХ, x — координата тела в момент времени t

Зная уравнение координаты, можно определить координату тела в любой момент времени.

Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.

Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x₀ = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с 2 . Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v₀ = 0 м/с.

В момент времени t = 10 c координата автомобиля равна:

Видео:Консультация по квантовой механике. Часть 5. "Волновая функция. Уравнение Шредингера"Скачать

Совместное движение двух тел

Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.

Аналитический способ решения задачи на совместное движение тел

Чтобы найти место встречи двух тел, нужно:

1. Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
2. Построить уравнение вида x₁ = x₂.
3. Найти время встречи двух тел t_встр.
4. Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату x_встрч.

Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с 2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.

Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:

x = 3t = 3∙6 = 18 (м).

Графический способ решения задачи на совместное движение тел

Существует графический способ решения данной задачи. Для этого нужно:

1. Построить графики x1(t) и x2(t).
2. Найти точку пересечения графиков.
3. Пустить перпендикуляр из этой точки к оси ОХ.
4. Значение точки пересечения — координата места пересечения двух тел.

Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!

Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием t_запазд, то его уравнение координаты принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с 2 и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с 2 , достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.

Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).

В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t:

В результате получаем два

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.

В момент времени t=0 проекции её скорости υ_x и ускорения a_x на ось Ох удовлетворяют соотношениям:

а)

б)

в)

г)

Алгоритм решения

1. Определить характер движения материальной точки.
2. Записать уравнение координаты материальной точки.
3. С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.

Решение Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

1. Записать исходные данные.
2. Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
3. Выразить скорость грузовика из уравнения его движения.
4. Записать уравнение движения мотоциклиста.
5. Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
6. Подставить время в формулу скорости грузовика и вычислить ее.

Решение

• Координата встречи грузовика и мотоциклиста: x = 150 м.
• Время запаздывания мотоциклиста: t_запазд = 5 с.
• Ускорение, с которым мотоциклист начал движение: a = 3 м/с 2 .

Запишем уравнение движения грузовика:

Так как начальная координата равна нулю, это уравнение примет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Отсюда скорость движения грузовика равна:

Запишем уравнение движения мотоциклиста:

Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:

Найдем время, через которое грузовик и мотоциклист встретились:

Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Видео:Физика. 9 класс. Уравнение колебательного движения /09.02.2021/Скачать

По уравнению зависимости координаты от времени x t 90 sin 4 пt определить

построить график зависимости

Тело без начальной скорости падает в шахту глубиной 100 км. Построить график зависимости мгновенной скорости от времени. Оценить максимальную скорость движения тела.

Закон движения грузика, прикрепленного к пружине, в отсутствие затухания имеет вид x(t) = x₀sin(ω₀t+φ), где амплитуда х₀ = 0,05 м, циклическая частота ω₀ = 6,28 с –1 , начальная фаза φ = π/2. 1. Определить начальную координату, начальные и максимальные значения скорости и ускорения грузика. 2. Построить графики зависимости координаты, скорости и ускорения от времени: x(t), v_x(t), a_x(t).

Уравнение прямолинейного движения имеет вид x = At+Bt 2 , где A = 3 м/с, B = -0,25 м/с 2 . Построить графики зависимости координаты и пути от времени для заданного движения.

На рисунке дан график зависимости ускорения от времени для некоторого движения тела. Построить графики зависимости скорости и пути от времени для этого движения, если в начальный момент тело покоилось.

Тело движется в направлении, противоположном оси Х, со скоростью 200 м/с. Построите график зависимости V_x(t). Найдите графически перемещение тела по оси Х за первые 4 с движения.

Найти зависимость теплопроводности λ от давления р при следующих процессах: 1) изотермическом; 2) изохорном. Изобразить эти зависимости на графиках.

Зависимость координаты Х от времени t определяется уравнением X = –1 + 2t – 3t 2 + 3t 3 . Определите зависимость скорости и ускорения от времени; расстояние, пройденное телом за t = 4 секунды от начала движения; скорость и ускорение тела через t = 4 секунды от начала движения; среднюю скорость и среднее ускорение за последнюю секунду движения. Постройте графики зависимости скорости и ускорения тела в промежутке времени от 0 до 4 секунд.

По приведенному графику построить графики зависимости углового ускорения и углового пути от времени, учитывая, что φ(0) = 0. Определить число оборотов, сделанное вращающимся телом за первые 6 с движения.

По заданному уравнению пройденного телом пути s = 4 + 2t + 5t 2 построить график зависимости скорости от времени за первые 3с. Определить расстояние, пройденное телом за это время?

Уравнение движения точки имеет вид x = –270+12t. По уравнению определить: 1) координату х₀ точки в начальный момент времени; 2) начальную скорость v₀ точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0

Уравнение движения точки имеет вид x = –1,5t. По уравнению определить: 1) координату х₀ точки в начальный момент времени; 2) начальную скорость v₀ точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0

Уравнение движения точки имеет вид x = 2+0,4t 2 . По уравнению определить: 1) координату х₀ точки в начальный момент времени; 2) начальную скорость v₀ точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0

Уравнение движения точки имеет вид x = 1–0,2t 2 . По уравнению определить: 1) координату х₀ точки в начальный момент времени; 2) начальную скорость v₀ точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0

Уравнение движения точки имеет вид x = –0,4t 2 . По уравнению определить: 1) координату х₀ точки в начальный момент времени; 2) начальную скорость v₀ точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0

Уравнение движения точки имеет вид x = 2+5t. По уравнению определить: 1) координату х₀ точки в начальный момент времени; 2) начальную скорость v₀ точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0

Уравнение движения точки имеет вид x = 150–10t. По уравнению определить: 1) координату х₀ точки в начальный момент времени; 2) начальную скорость v₀ точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0

Уравнение движения точки имеет вид x = 400–0,6t. По уравнению определить: 1) координату х₀ точки в начальный момент времени; 2) начальную скорость v₀ точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0

Уравнение движения точки имеет вид x = 10t+0,4t 2 . По уравнению определить: 1) координату х₀ точки в начальный момент времени; 2) начальную скорость v₀ точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0

Уравнение движения точки имеет вид x = 2t–t 2 . По уравнению определить: 1) координату х₀ точки в начальный момент времени; 2) начальную скорость v₀ точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0

Конденсатор емкостью 2 мкФ зарядили до напряжения 80 В и подключили к катушке с индуктивностью 350 мГн. После этого в контуре возникли гармонические колебания. Запишите уравнение для силы тока в колебательном контуре и постройте график зависимости силы тока в контуре от времени. Найдите максимальную энергию магнитного поля в контуре.

В электрической цепи с малым активным сопротивлением, содержащей конденсатор емкостью C = 0,2 мкФ и катушку индуктивностью L = 1 мГн, сила тока при резонансе изменяется по закону I = 0,02sinωt. Найти мгновенное значение силы тока, а также мгновенные значения напряжения на конденсаторе и катушке через 1/3 периода от начала возникновения колебаний. Построить графики зависимости силы тока и напряжений от времени.

При помощи векторной диаграммы сложить 3 сонаправленных колебания: х₁ = 3·cos(ω·t), см; x₂ = 3·sin(ω·t), см; х₃ = 6·sin(ω·t + π), см. Записать уравнение результирующего колебания, если ω = π/2 рад/с. Построить график зависимости х_рез от времени.

Конденсатор емкостью 0,5 мкФ зарядили до напряжения 20 В и подключили к катушке с индуктивностью 0,65 Гн и сопротивлением 46 Ом. Найдите уравнение для силы тока в колебательном контуре. Через сколько времени амплитуда силы тока уменьшится в 4 раза? Постройте график зависимости силы тока от времени.

Во сколько раз следует увеличить изотермически объем 4 моль идеального газа, чтобы его энтропия испытала приращение равное 23 Дж/К? Постройте график зависимости энтропии от объема.

Закон движения грузика, прикрепленного к пружине, в отсутствии затухания имеет вид Х(t) = x₀ Sin (wt + φ₀), где x₀ = 0,03м — амплитуда колебания, w = 6,28рад/с — циклическая частота, φ₀ = π/4 — начальная фаза. Определить начальную координату, начальные и максимальные значения скорости и ускорения грузика. Построить графики зависимости координаты, скорости и ускорения от времени.

Тело движется по закону x = t 3 –12t. (Все величины заданы в системе СИ). Определите начальные скорость и ускорение тела. Постройте графики зависимости координаты, скорости и ускорения тела от времени. В какой момент времени тело остановится? Чему равна его координата в этот момент времени?

По результатам измерений построены графики зависимости коэффициента затухания β от сопротивления R колебательного контура. Который из контуров имеет большую индуктивность?

Зависимость координаты материальной точки от времени выражается уравнением: x(t) = 1,5t 2 –0,25t 3 , м. Вычислите: 1) зависимость скорости и ускорения от времени; 2) скорость и ускорение в момент времени t = 1 c; 3) максимальную скорость точки; 4) перемещение через 3 с от начала движения; 5) постройте графики зависимостей: x = f(t), v = f(t), a = f(t); 6) назовите характер движения тела.

Энергия ионизации гелия равна 24,5 эВ, неона — 21,5 эВ, криптона — 14 эВ и ксенона — 12,1 эВ. Постройте график зависимости потенциала ионизации от порядкового номера в таблице Менделеева. По графику вычислите энергию ионизации аргона.

Тангенциальное ускорение точки меняется согласно графику. Выберите график зависимости скорости от времени, соответствующая такому движению. Ответ обоснуйте. Постройте схематично график зависимости координаты от времени.

📸 Видео

Решение задач по термохимическим уравнениям. Практическое занятие. Видеоурок 40. Химия 9 классСкачать

Урок 119 (осн). Плавление и кристаллизация. Удельная теплота плавленияСкачать

Вся механика для ЕНТ по физике за 5 часовСкачать

Раскидал все графики из нового задания № 2. ФИЗИКА ЕГЭ 2022Скачать

Урок 127 (осн). Задачи на уравнение теплового баланса - 1Скачать

ВСЕ ФОРМУЛЫ ПО ФИЗИКЕ I Финальный Курс I ЕГЭ 2024 I Эмиль Исмаилов - Global_EEСкачать

прямолинейное РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ | формулы кинематикиСкачать