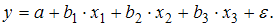 Число степеней свободы остаточной суммы квадратов отклонений для этого уравнения равно …
Число степеней свободы остаточной суммы квадратов отклонений для этого уравнения равно …Число степеней свободы для остаточной регрессии может быть определено по формуле (n – m – 1), где n – число наблюдений, m – число параметров перед переменными в уравнении множественной регрессии. Значит в нашем случае число степеней свободы для остаточной регрессии равно 50 – 3 –1= 46.
Магнус, Ян Р. Эконометрика : нач. курс : [учеб. для студентов вузов по экон. специальностям] / Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий ; Акад. нар. хоз-ва при Правительстве РФ. – М. : Дело, 2005. C. 67–70.
ответ тест i-exam
Видео:Эконометрика. Множественная регрессия и корреляция.Скачать

Вопрос Пусть y
| Название | Вопрос Пусть y |
| Дата | 04.03.2018 |
| Размер | 0.76 Mb. |
| Формат файла |  |
| Имя файла | Test_RAVANDA_2.docx |
| Тип | Документы #37687 |
| страница | 3 из 8 |
| Подборка по базе: Ответы на вопросы к госам.docx, Ответы на вопросы экзамена ТиМФК.docx, 2. Вопросы по дисциплине __МАРКЕТИНГ__.doc, кл.рук вопрос 8.odt, конт вопросы.docx, Ответы на вопросы к экзамену по общей психологии.docx, Вариант 2 Вопросы.docx, Вариант 1 Вопросы.docx, ответы на вопросы.docx, artterapia вопросы к зачету.docx При расчете скорректированного коэффициента множественной детерминации пользуются формулой + n – число наблюдений; m – число факторов, включенных в модель множественной регрессии − m – число наблюдений; n – число факторов, включенных в модель множественной регрессии − n – число параметров при независимых переменных; m – число факторов, включенных в модель множественной регрессии − n – число параметров при независимых переменных; m – число наблюдений Если для среднеквадратической ошибки параметра и значения оценки этого параметра линейной эконометрической модели выполняется соотношение − ненадежности среднеквадратической ошибки − надежности среднеквадратической ошибки Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции … + первого, второго, третьего и последующих порядков − между трендовой, сезонной и случайной компонентами − между несколькими временными рядами − факторов, формирующих уровень ряда Известно, что временной ряд Y порожден случайным процессом, который по своим характеристикам является «белым шумом». Значит, ряд Y … Изучаются модели зависимости спроса и предложения от цены p и прочих факторов. Установите соответствие между видом и классом эконометрических уравнений. 1 система независимых уравнений 2 система одновременных уравнений 3 система рекурсивных уравнений система приведенных уравнений Модель равенства спроса и предложения, где предложение и спрос являются линейными функциями цены p, состоит из уравнений … + + − − Дана приведенная форма модели системы одновременных уравнений: 1 эндогенная переменная 2 экзогенная переменная системы 3 приведенный коэффициент Степенной моделью не является регрессионная модель … + − − − При расчете уравнения нелинейной регрессии Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле При нарушении гомоскедастичности остатков и наличии автокорреляции остатков рекомендуется применять _____________ метод наименьших квадратов. Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет … Для эконометрической модели линейного уравнения множественной регрессии вида По результатам 50 статистических наблюдений построено уравнение множественной регрессии Для эконометрической модели вида Для уравнения множественной регрессии вида − − − Для регрессионной модели Для линеаризации нелинейной регрессионной модели − − − В состав любого временного ряда, построенного по реальным данным, обязательно входит _____ компонента. Значение коэффициента автокорреляции первого порядка характеризует … + тесноту линейной связи − качество модели временного ряда − тесноту нелинейной связи Известно, что дисперсия временного ряда Y увеличивается с течением времени. Значит, ряд Y … Дана автокорреляционная функция временного ряда + имеет выраженную сезонную компоненту с лагом 4 − содержит только тенденцию, и не содержит сезонной компоненты − имеет выраженную сезонную компоненту с лагом 6 − не имеет ни тенденции, ни сезонной компоненты, имеет только случайную компоненту Для мультипликативной модели временного ряда Y = T · S · E сумма скорректированных сезонных компонент равна … Известно, что доля остаточной регрессии в общей составила 0,19. Тогда значение коэффициента корреляции равно … Для уравнения множественной регрессии вида + − − − Дана таблица исходных данных для построения эконометрической регрессионной модели: Фиктивными переменными не являются … Видео:Множественная регрессия в ExcelСкачать  Тема 10: Оценка качества подбора уравнения1. Известно, что доля остаточной регрессии в общей составила 0,19. Тогда значение коэффициента корреляции равно … Решение: Известно, что доля остаточной регрессии в общей составила 0,19. Значит, 2. Известно, что общая сумма квадратов отклонений Решение: Для расчета коэффициента детерминации можно пользоваться следующей формулой: 3. Для регрессионной модели вида Решение: Значение коэффициента детерминации 4. Если общая сумма квадратов отклонений Решение: Общая сумма квадратов отклонений складывается из суммы квадратов отклонений, объясненных регрессией, и остаточной сумма квадратов отклонений. Тема 11: Проверка статистической значимости эконометрической модели 1. При расчете скорректированного коэффициента множественной детерминации пользуются формулой n – число наблюдений; m – число факторов, включенных в модель множественной регрессии m – число наблюдений; n – число факторов, включенных в модель множественной регрессии n – число параметров при независимых переменных; m – число факторов, включенных в модель множественной регрессии n – число параметров при независимых переменных; m – число наблюдений Решение: Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и имеет вид 2. Если известно уравнение множественной регрессии Решение: Расчет F-статистики начинается с разложения общей суммы квадратов отклонений на сумму квадратов отклонений, объясненную регрессией, и остаточную сумму квадратов отклонений: В нашем случае дано Существует равенство между числом степеней свободы общей, факторной и остаточной сумм квадратов отклонений: n – 1 = m + (n – m – 1), где n –число наблюдений, m – число параметров перед переменными в уравнений регрессии. Число степеней свободы для общей суммы квадратов отклонений равно n – 1. В нашем случае n – 1 = 49. Число степеней свободы для остаточной суммы квадратов отклонений равно n – m – 1 = 46. Число степеней свободы для факторной суммы квадратов отклонений равно m = 3. Рассчитаем факторную и остаточную дисперсии на одну степень свободы по формулам 3. Для регрессионной модели известны следующие величины дисперсий: Решение: Назовем приведенные дисперсии: Тема 12: Оценка значимости параметров эконометрической модели 1. Для уравнения множественной регрессии вида Решение: Чтобы оценить значимость параметров регрессии используется t-критерий Стьюдента. Для каждого коэффициента регрессии 2. Если для среднеквадратической ошибки ненадежности среднеквадратической ошибки надежности среднеквадратической ошибки Решение: Превышение среднеквадратической ошибки параметра над значением его оценки свидетельствует о статистической ненадежности параметра. 3. Для уравнения множественной регрессии вида Для данного уравнения при уровне значимости α=0,05 значимыми являются параметры … Решение: Чтобы оценить значимость параметров регрессии используется t-критерий Стьюдента. Для каждого коэффициента регрессии 4. Проверка статистически значимого отличия от нуля оценок коэффициентов Решение: При проверке статистически значимого отличия от нуля оценок коэффициентов Тема 13: Нелинейные зависимости в экономике 1. Если зависимость объема спроса от цены характеризуется постоянной эластичностью, то моделирование целесообразно проводить на основе … параболы второй степени Решение: Из перечисленных функций только степенная функция характеризуется постоянной эластичностью, следовательно, ее и нужно применить для отражения данной зависимости. 2. Если по результатам анализа поля корреляции замечено, что на интервале изменения фактора меняется характер связи рассматриваемых признаков, прямая связь изменяется на обратную, то моделирование целесообразно проводить на основе … параболы второй степени параболы третьей степени Решение: Параболу второй степени целесообразно применять в случае, когда на интервале изменения фактора меняется характер связи рассматриваемых признаков, прямая связь изменяется на обратную или обратная на прямую. 3. Нелинейное уравнение регрессии вида Решение: Нелинейное уравнение регрессии вида 4. Если с увеличением масштабов производства удельный расход сырья сокращается, то моделирование целесообразно проводить на основе … параболы второй степени Решение: Равносторонняя гипербола обычно используется в эконометрике для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, поскольку она позволяет учесть эффект масштаба, что с увеличением объемов выпускаемой продукции удельные показатели расходов сырья, материалов или топлива обычно падают. Тема 14: Виды нелинейных уравнений регрессии 1. Степенной моделью не является регрессионная модель … Решение: Степенной моделью регрессии является такая модель, в которой независимая переменная х стоит в основании степени, а параметр – в показателе. Такими моделями из приведенных в ответах являются уравнения: В уравнении 2. Среди предложенных нелинейных зависимостей нелинейной по параметрам является … Решение: Среди предложенных нелинейных зависимостей зависимость 3. Среди предложенных нелинейных зависимостей нелинейной существенно (внутренне нелинейной) является … Решение: Среди предложенных нелинейных зависимостей зависимость 4. Среди предложенных нелинейных зависимостей внутренне линейной является … Решение: Среди предложенных нелинейных зависимостей зависимость Тема 15: Линеаризация нелинейных моделей регрессии 1. Для линеаризации нелинейной регрессионной модели приведение уравнения к виду 1/y Решение: Линеаризация – это процедура приведения нелинейной регрессионной модели к линейному виду путем различных математических преобразований. Нелинейная модель 2. Для преобразования внутренне нелинейной функции разложения функции в ряд Тейлора Решение: Функция 3. Для линеаризации нелинейной функции логарифмирования и замены переменных разложения функции в ряд Тейлора потенцирования и замены переменных обращения и замены переменных Решение: Функция Тема 16: Оценка качества нелинейных уравнений регрессии 1. При расчете уравнения нелинейной регрессии Решение: Доля остаточной дисперсии в общей меньше 20%, значит, доля объясненной регрессии в общей больше 80%, другими словами, коэффициент детерминации больше 0,8. Поскольку коэффициент детерминации может принимать значения только в интервале [0, 1], то отрезком минимальной длины, в который попадает коэффициент детерминации для данной модели, будет отрезок [0,8; 1]. 2. По 20 регионам страны изучалась зависимость уровня безработицы y (%) от индекса потребительских цен x (% к предыдущему году) и построено уравнение в логарифмах исходных показателей: Решение: Коэффициент детерминации для модели в исходных показателях в данном случае будет равен коэффициенту детерминации для модели в логарифмах исходных показателей, который вычисляется как квадрат коэффициента корреляции, то есть 0,64. 3. Для регрессионной модели Решение: Значение индекса детерминации R 2 характеризует долю дисперсии зависимой переменной, объясненную независимой переменной (построенным нелинейным уравнением регрессии). Разность (1-R 2 ) характеризует долю дисперсии зависимой переменной, необъясненную уравнением, эту величину и необходимо определить в задании. Воспользуемся формулой для расчета R 2 : 4. Для регрессионной модели Решение: Величина, характеризующая долю дисперсии зависимой переменной, объясненную независимой переменной (построенным нелинейным уравнением регрессии), называется индексом (коэффициентом) детерминации – R 2 . Значения индекса детерминации R 2 и индекса корреляции R для нелинейных регрессионных моделей связаны соотношением 5. По результатам проведения исследования торговых точек было построено уравнение нелинейной регрессии при уровне значимости при уровне значимости эластичность спроса по цене составляет –0,8 при уровне значимости Решение: Для проверки значимости коэффициентов нелинейной регрессии, после линеаризации, как и для уравнения парной линейной регрессии, применяется стандартный алгоритм критерия Стьюдента. Для b формулируется нулевая гипотеза Тема 17: Временные ряды данных: характеристики и общие понятия 1. В состав любого временного ряда, построенного по реальным данным, обязательно входит _____ компонента. Решение: Ряд, построенный по реальным данным, может не содержать тренда, сезонной (циклической) компоненты, однако, он обязательно содержит случайную компоненту. 2. Ряд, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, изображен на графике … Решение: График ряда, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, будет колебаться относительно своего среднего значения. 3. Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется … Решение: Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется временным рядом. 4. Выраженную положительную тенденцию содержит ряд … Решение: Ряд имеет выраженную положительную тенденцию, если уровни ряда увеличиваются с увеличением периода времени t. Тема 18: Структура временного ряда 1. Значение коэффициента автокорреляции первого порядка характеризует … тесноту линейной связи качество модели временного ряда тесноту нелинейной связи Решение: Структура временного ряда определяется по значениям коэффициента автокорреляции, рассчитанным для разных порядков коэффициента автокорреляции. Коэффициент автокорреляции характеризует тесноту связи между уровнями исходного ряда и уровнями этого же ряда, сдвинутыми на значение порядка, а само значение коэффициента корреляции рассчитывается по аналогии с парным коэффициентом линейной корреляции и характеризует тесноту линейной связи между двумя переменными. Поэтому варианты «качество модели временного ряда», «тесноту нелинейной связи» и «значимость тренда» являются неверными. 🔥 ВидеоМножественная регрессияСкачать  Множественная регрессия в Excel и мультиколлинеарностьСкачать  Эконометрика. Построение модели множественной регрессии в Excel.Скачать  РЕГРЕССИОННЫЙ АНАЛИЗ STATISTICA #12Скачать  Эконометрика Линейная регрессия и корреляцияСкачать  Эконометрика. Линейная парная регрессияСкачать  EViews. Урок 1. Построение модели множественной регрессии.Скачать  09 02 Основы множественной регрессииСкачать  Тема по SPSS: множественная линейная регрессия - одновременное включение всех переменных в модель.Скачать  Построение модели множественной регрессии в программе GretlСкачать  РЕГРЕССИОННЫЙ АНАЛИЗ общая идея | АНАЛИЗ ДАННЫХ #16Скачать  Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать  Множественная степенная регрессияСкачать  Парная регрессия: линейная зависимостьСкачать  Уравнение множественной регрессии в ExcelСкачать  Математика #1 | Корреляция и регрессияСкачать  Множественная линейная регрессия в StatisticaСкачать  Парная и множественная линейная регрессияСкачать 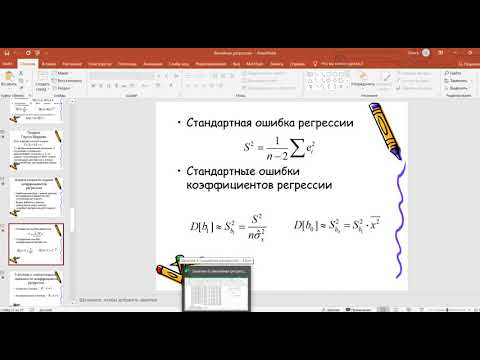 |
 , где …
, где … , то это свидетельствует о статистической ______ параметра.
, то это свидетельствует о статистической ______ параметра.











 , где y – спрос на продукцию, ед.; x – цена продукции, руб., выяснилось, что доля остаточной дисперсии в общей меньше 20%. Коэффициент детерминации для данной модели попадает в отрезок минимальной длины …
, где y – спрос на продукцию, ед.; x – цена продукции, руб., выяснилось, что доля остаточной дисперсии в общей меньше 20%. Коэффициент детерминации для данной модели попадает в отрезок минимальной длины … , где – значение коэффициента автокорреляции остатков модели. Минимальная величина значения будет наблюдаться при ________ автокорреляции остатков.
, где – значение коэффициента автокорреляции остатков модели. Минимальная величина значения будет наблюдаться при ________ автокорреляции остатков. построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х (1) , х (2) , х (3) , x (4) – независимые переменные):
построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х (1) , х (2) , х (3) , x (4) – независимые переменные):
 Число степеней свободы остаточной суммы квадратов отклонений для этого уравнения равно …
Число степеней свободы остаточной суммы квадратов отклонений для этого уравнения равно … показателем тесноты связи между переменными и является парный коэффициент линейной …
показателем тесноты связи между переменными и является парный коэффициент линейной … на основании 14 наблюдений рассчитаны оценки параметров и записана модель:
на основании 14 наблюдений рассчитаны оценки параметров и записана модель:






 , где – нелинейная функция,
, где – нелинейная функция,  – рассчитанное по модели значение переменной , получены значения дисперсий:
– рассчитанное по модели значение переменной , получены значения дисперсий:  . Не объяснена моделью часть дисперсии переменной , равная …
. Не объяснена моделью часть дисперсии переменной , равная … используется замена …
используется замена …



 (в скобках указаны значения t-статистики, соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости
(в скобках указаны значения t-статистики, соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости



 Найдем коэффициент детерминации:
Найдем коэффициент детерминации:  Вычислим коэффициент корреляции:
Вычислим коэффициент корреляции: 
 , а остаточная сумма квадратов отклонений,
, а остаточная сумма квадратов отклонений,  . Тогда значение коэффициента детерминации равно …
. Тогда значение коэффициента детерминации равно …

 . Значит, в нашем случае коэффициент детерминации равен:
. Значит, в нашем случае коэффициент детерминации равен: 
 , где
, где  рассчитаны дисперсии:
рассчитаны дисперсии:  ;
;  ;
;  . Тогда величина
. Тогда величина  характеризует долю …
характеризует долю … характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной. Разность
характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной. Разность  характеризует долю остаточной дисперсии, которая может быть рассчитана также по формуле
характеризует долю остаточной дисперсии, которая может быть рассчитана также по формуле  , и остаточная сумма квадратов отклонений
, и остаточная сумма квадратов отклонений 
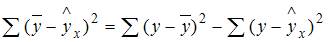
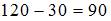 .
. , где …
, где … построенное по результатам 50 наблюдений, для которого общая сумма квадратов отклонений равна 153, и остаточная сумма квадратов отклонений равна 3, то значение F-статистики равно …
построенное по результатам 50 наблюдений, для которого общая сумма квадратов отклонений равна 153, и остаточная сумма квадратов отклонений равна 3, то значение F-статистики равно … , где
, где – общая сумма квадратов отклонений
– общая сумма квадратов отклонений – сумма квадратов отклонений, объясненная регрессией
– сумма квадратов отклонений, объясненная регрессией – остаточная сумма квадратов отклонений
– остаточная сумма квадратов отклонений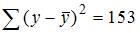 ,
,  . Следовательно,
. Следовательно, 




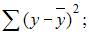
 где y – значение зависимой переменной по исходным данным;
где y – значение зависимой переменной по исходным данным;  – значение зависимой переменной, вычисленное по регрессионной модели;
– значение зависимой переменной, вычисленное по регрессионной модели;  – среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство …
– среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство …



 – общая дисперсия;
– общая дисперсия;  – объясненная дисперсия;
– объясненная дисперсия;  – остаточная дисперсия. При анализе статистической модели величину общей дисперсии рассматривают как сумму объясненной и остаточной дисперсий, поэтому справедливо равенство:
– остаточная дисперсия. При анализе статистической модели величину общей дисперсии рассматривают как сумму объясненной и остаточной дисперсий, поэтому справедливо равенство: 
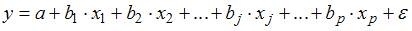 на основании 14 наблюдений рассчитаны оценки параметров и записана модель:
на основании 14 наблюдений рассчитаны оценки параметров и записана модель:  (в скобках указаны значения t-статистики, соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости
(в скобках указаны значения t-статистики, соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости 






 формулируется нулевая гипотеза
формулируется нулевая гипотеза 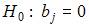 при альтернативной гипотезе
при альтернативной гипотезе  Затем рассчитывается фактическое значение t-статистики, которое сравнивается с критическим значением Стьюдента
Затем рассчитывается фактическое значение t-статистики, которое сравнивается с критическим значением Стьюдента  для требуемого числа степеней свободы и уровня значимости. Если
для требуемого числа степеней свободы и уровня значимости. Если  , коэффициент
, коэффициент  значим; если
значим; если  коэффициент
коэффициент 
 параметра и значения оценки этого параметра
параметра и значения оценки этого параметра  линейной эконометрической модели выполняется соотношение
линейной эконометрической модели выполняется соотношение  , то это свидетельствует о статистической ______ параметра.
, то это свидетельствует о статистической ______ параметра. (в скобках указаны значения t-статистики соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости
(в скобках указаны значения t-статистики соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости 
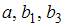

 . Затем рассчитывается фактическое значение t-статистики, которое сравнивается с критическим значением Стьюдента
. Затем рассчитывается фактическое значение t-статистики, которое сравнивается с критическим значением Стьюдента  для требуемого числа степеней свободы и уровня значимости. Если
для требуемого числа степеней свободы и уровня значимости. Если 
 линейной модели
линейной модели 
 (
(  –среднеквадратическая ошибка параметра
–среднеквадратическая ошибка параметра  модели рассчитывают отношение его среднеквадратической ошибки к значению оценки
модели рассчитывают отношение его среднеквадратической ошибки к значению оценки  является _____ моделью ________ регрессии.
является _____ моделью ________ регрессии. , а количество независимых переменных х равно единице.
, а количество независимых переменных х равно единице.


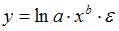

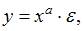







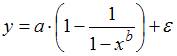

 Остальные виды линеаризации не позволяют линеаризовать исходную нелинейную модель.
Остальные виды линеаризации не позволяют линеаризовать исходную нелинейную модель. является внутренне линейной и с помощью логарифмирования может быть преобразована к виду
является внутренне линейной и с помощью логарифмирования может быть преобразована к виду  , которая является линейной относительно логарифмов переменных. Сделав замену переменных
, которая является линейной относительно логарифмов переменных. Сделав замену переменных  ,
,  ,
,  ,
,  , получим линейную функцию
, получим линейную функцию  . Поэтому для линеаризации используется сначала логарифмирование, затем замена переменных.
. Поэтому для линеаризации используется сначала логарифмирование, затем замена переменных. , где y – спрос на продукцию, ед.; x – цена продукции, руб., выяснилось, что доля остаточной дисперсии в общей меньше 20%. Коэффициент детерминации для данной модели попадает в отрезок минимальной длины …
, где y – спрос на продукцию, ед.; x – цена продукции, руб., выяснилось, что доля остаточной дисперсии в общей меньше 20%. Коэффициент детерминации для данной модели попадает в отрезок минимальной длины … . Коэффициент корреляции между логарифмами исходных показателей составил
. Коэффициент корреляции между логарифмами исходных показателей составил  . Коэффициент детерминации для модели в исходных показателях равен …
. Коэффициент детерминации для модели в исходных показателях равен …
 , где
, где 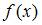 – нелинейная функция,
– нелинейная функция,  – рассчитанное по модели значение переменной
– рассчитанное по модели значение переменной  , получены значения дисперсий:
, получены значения дисперсий:  . Не объяснена моделью часть дисперсии переменной
. Не объяснена моделью часть дисперсии переменной  . Следовательно, разность
. Следовательно, разность  . Таким образом, часть дисперсии переменной
. Таким образом, часть дисперсии переменной 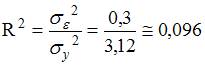




 . Следовательно, значение
. Следовательно, значение  .
. ,
,  ,
,  , то …
, то … можно считать, что эластичность спроса по цене составляет –0,8
можно считать, что эластичность спроса по цене составляет –0,8 можно считать, что эластичность спроса по цене составляет –0,8
можно считать, что эластичность спроса по цене составляет –0,8 можно считать, что эластичность спроса по цене составляет –0,8
можно считать, что эластичность спроса по цене составляет –0,8 при альтернативной гипотезе
при альтернативной гипотезе  . Затем рассчитывается фактическое значение t-статистики, которое сравнивается с критическим значением Стьюдента
. Затем рассчитывается фактическое значение t-статистики, которое сравнивается с критическим значением Стьюдента  значим; если
значим; если  , коэффициент
, коэффициент 



 —
—