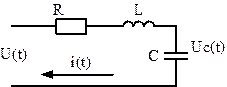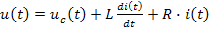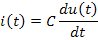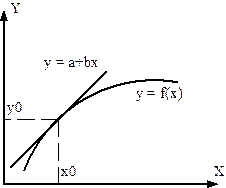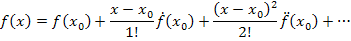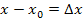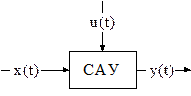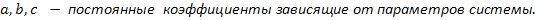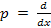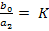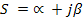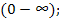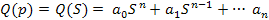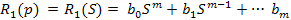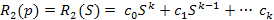По основным видам уравнений динамики процессов управления системы подразделяются на (6 видео)

Классификация систем автоматического управления

Все системы автоматического управления и регулирования делятся по различным признакам на

следующие основные классы:

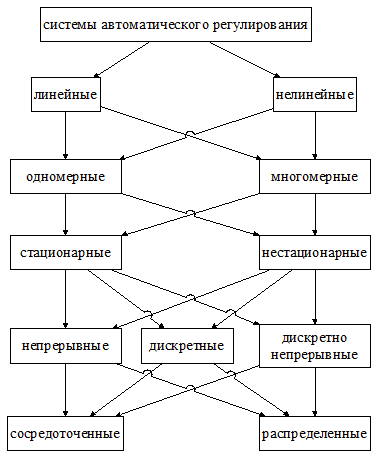
1. По основным видам уравнений динамики процессов управления:

а) линейные системы;

б) нелинейные системы.

2. По количеству управляющих параметров: одномерные (одноканальные) и многомерные (многоканальные).

3. По характеру представления сигналов различают:

а) непрерывные системы;

б) дискретные системы, среди которых выделяют импульсные, релейные, цифровые.

4. По характеру процессов управления:

а) детерминированные системы – системы с определенными переменными и процессами;

5. По характеру функционирования.

В зависимости от того, по какому закону изменяется заданное значение регулируемой величины,

системы автоматического управления подразделяются на:

а) системы стабилизации, поддерживающие постоянство регулируемой величины, т.е. yзад(t) = const;

б) системы программного регулирования, в которых заданное значение регулируемой величины изменяется по определенной заранее временной программе;

в) следящие системы, в которых заданное значение регулируемой величины изменяется в соответствии с состоянием некоторого заданного вектора переменных во времени;

г) системы оптимального управления, в которых показатель эффективности зависит не только от текущих значений координат но также от характера их изменения в прошлом, настоящем и будущем. Нахождение оптимального управления предполагает решение достаточно сложной математической задачи соответствующими методами, кроме того органической составной частью системы является компьютер;

д) адаптивные системы, в которых автоматически изменяются значения yзад , собственные параметры или структура при непредвиденных изменениях внешних условий на основании анализа состояния или поведения системы так, чтобы сохранялось заданное качество ее работы.

Системы с изменением заданного значения регулируемой величины называют экстремальными, с изменением параметров – самонастраивающимися, с изменением структуры – самоорганизующимися.

Математическое описание одномерных элементов и систем автоматического управления. Общие положения. Передаточные функции.

3.1. Общие положения.

Одномерными являются системы, которые имеют одну входную и одну выходную величину. Так как в электроэнергетике большинство систем являются одномерными, рассмотрим их математическое описание более подробно.

Поведение САУ в процессе функционирования представляют собой объединение статических и динамических режимов. Для проведения теоретических исследований САУ и её отдельных элементов необходимо иметь уравнения, которые описывают их поведение при внешних воздействиях, которые изменяются. Эти уравнения представляют собой выраженные в математической форме соотношения, которые связывают входные и выходные сигналы и воздействия.

С целью упрощения получения математических соотношений обычно вводят следующие допущения:

— САУ и её элементы имеют свойство стационарности.

— элементы САУ линейные

— процессы, протекающие в системе, являются непрерывными функциями времени при нулевых начальных условиях.

3.2. Математические модели. Линеаризация.

Во-первых, математические модели могут быть получены теоретически из законов физики(законы сохранения массы, энергии, импульса). Эти модели описывают внутренние связи в объекте и, как правило, наиболее точны.

Рассмотрим RLC-цепочку, то есть последовательное соединение резистора с сопротивлением R, катушки индуктивности с индуктивностью L и конденсатора с емкостью C. Она может быть описана с помощью двух уравнений:

Второй способ – построение модели в результате наблюдения за объектомпри различных входных сигналах (этим занимается теория идентификации). Объект рассматривается как «черный ящик», то есть, его внутреннее устройство неизвестно. Мы смотрим, как он реагирует на входные сигналы, и стараемся подстроить модель так, чтобы выходы модели и объекта совпадали как можно точнее при разнообразных входах.

На практике часто используется смешанный способ: структура модели (вид уравнения, связывающего вход и выход) определяется из теории, а коэффициенты находят опытным путем. Например, общий вид уравнений движения корабля хорошо известен, однако в этих уравнениях есть коэффициенты, которые зависят от многих факторов (формы корпуса, шероховатости поверхности и т.п.), так что их крайне сложно (или невозможно) найти теоретически. В этом случае для определения неизвестных коэффициентов строят масштабные модели и испытывают их в бассейнах по специальным методикам. В авиастроении для тех же целей используют аэродинамические трубы.

Для любого объекта управления можно построить множество различных моделей, которые будут учитывать (или не учитывать) те или иные факторы.

Обычно используется компромиссный вариант. Начинают с простых моделей, стараясь спроектировать регулятор так, чтобы он «подходил» и для сложной модели. Затем проверяют работу построенного закона управления на полной модели или на реальном объекте. Если получен отрицательный результат (простой регулятор «не работает»), усложняют модель, вводя в нее дополнительные подробности.

Линеаризация.

Из курса математики известно, что проще всего решать линейные уравнения. С нелинейными уравнениями (квадратными, кубическими и др.) работать намного сложнее, многие типы уравнений математика пока не умеет решать аналитически (точно).

Однако, все модели реальных систем – нелинейные. Это легко понять хотя бы потому, что всегда есть предельно допустимое значение входного сигнала – при его превышении объект может просто выйти из строя или даже разрушиться (линейность нарушается). Методы исследования нелинейных операторов очень сложны математически, в теории нелинейных систем точные решения известны только для достаточно узкого круга задач. Во многих случаях более или менее точные модели представляют собой нелинейные дифференциальные уравнения, поэтому для того, чтобы применить теорию линейных систем, требуется линеаризация. Идея линеаризации заключается в том, что в системах регулирования сигналы мало отклоняются от рабочей точки – некоторого положения равновесия, в котором все сигналы имеют установившиеся значения и их производные равны нулю. Поэтому для решения задач управления часто достаточно использовать линейную модель в отклонениях от этой рабочей точки.

Дальше для линеаризации используется разложение функций в ряд Тейлора. Для некоторой функции f (x) в окрестности точки (x0) этот ряд имеет вид:

Рассмотрим САУ общем виде. Структура представлена на рис. 3.1.

Рис. 3.1 Система автоматического управления.

Где Х(t) U(t) входные воздействия, а Y(t) – выходной параметр.

В общем виде функционирование непрерывной, линейной САУ описывается неоднородным дифференциальным уравнением следующего вида:

(1)

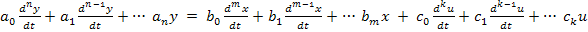
Где:

Введем оператор дифференцирования

Тогда уравнение (1) может быть представлено в операторном виде:

(2)

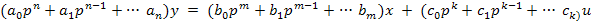
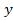
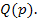
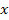
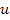
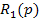
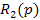
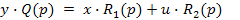
В выражении (2) полином, стоящий при выходной переменной называется собственным оператором и обозначается Полиномы при входных параметрах и называются соответственно оператором управляющего воздействия и оператором возмущающего воздействия и обозначаются и , а уравнение (2) принимает вид:

(3)

Если рассматривать установившийся режим то уравнение (2) примет вид:

(4)

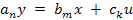
Уравнение (2) описывает поведение САУ как в динамике, так и в статике, а уравнение (4) только в статике.

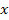
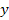
В тех случаях когда система или элемент описывается дифференциальным уравнением не выше второго порядка, используется стандартная система записи уравнения. Например , имеем САУ, которая содержит один вход и один выход , которая описывается уравнением

(5)

Левую и правую части уравнения (5) разделим на коэффициент :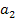

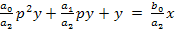
(6)

Введем обозначения: , ,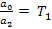

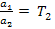
Тогда уравнение (6) принимает вид:

(7)

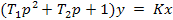
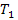
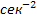
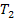
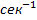
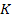
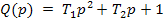
В уравнении (7) параметр имеет размерность , параметр имеет размерность , а параметр безразмерный. Выражение (7) представляет собой уравнение в стандарной форме, которая наиболее удобна для дальнейшего анализа динамических процессов. В этом случае собственный оператор принимает вид алгебраического уравнения:

(8)

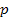
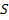
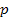
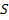
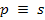
Необходимо отметить, что оператор дифференцирования имеет тесную связь с оператором интегрального преобразования Лапласа , который является комплексною величиной. Как известно, для линейных дифференциальных уравнений с постоянными параметрами при нулевых начальных условиях и точностью до обозначения оператор соответствует оператору , т.е. .

Это обстоятельство позволяет использовать для решения уравнений типа (1) и для моделирования САУ интегральное преобразование Лапласа.

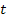
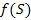
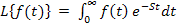
Напомним, что для преобразования функции действительной переменной на комплексной площади в функцию комплексной переменной используется выражение прямого преобразования Лапласа:

(9)

Где:

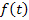
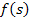
При этом функция называется оригиналом, а изображением.

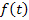
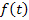
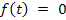
Функция имеет следующие особенности:

— — определена и кусочно-дифференцируема на всей положительной числовой оси

— при .

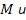
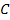
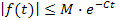
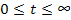
— Существуют такие положительные числа , для которых выполняется соотношение:

при .

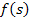
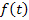
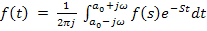
Переход от изображения к оригиналу (обратное преобразование Лапласа) выполняется следующим образом:

(10)

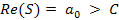
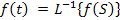
Здесь интегрирование происходит вдоль любой прямой, которая удовлетворяет условиям . Символически обратное преобразование Лапласа обозначается в виде:

(11)

3.3. Передаточные функции.

Понятие передаточная функция является наиболее важной категорией в теории автоматического управления и регулирования. Передаточная функция есть своего рода математической моделью САР, потому что полностью характеризует динамические параметры системы.

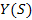
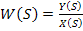
Передаточная функция представляет собой отношение изображения по Лапласу выходной величины к изображению входной величины , т.е. :

(12)

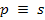
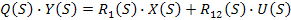
Исходя и условия для линейных систем уравнение (3) запишем в следующем виде:

(13)

Так как для линейных систем можно использовать принцип наложения, то возможно рассмотрение двух следующих случаев:

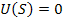
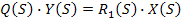
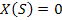
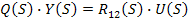
— сигнал , тогда ;

Тогда, для любой САР, которая имеет входы управления и возмущения можно найти две передаточные функции:

(14)

(15)

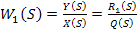
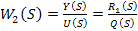
Уравнение (14) является передаточной функцией по управлению, а выражение (15) передаточной функцией по возмущению.

Собственный оператор

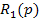
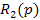
Соответственно оператор управляющего воздействия и оператор возмущающего выразим в таком же виде.

Следовательно, передаточные функции по управлению и по возмущающему воздействию будут представлять собой отношения следующих полиномов:

(16)

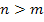
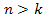
Для физической реализации необходимо чтобы выполнялись следующие условия и .

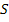
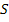
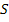
Передаточные функции представляют особые точки на комплексной площади – нули и полюса. Полюса это те значения , при которых передаточная функция стремится в бесконечность. Для определения полюсов необходимо собственный оператор (знаменатель передаточной функции) приравнять нулю и решить алгебраическое уравнение относительно . Нули – это такие значения , при который передаточная функция равняется нулю. Для определения нулей числитель передаточной функции приравнивается нулю и полученное алгебраическое уравнение решается относительно .

Если задана структура САР, то можно определить передаточную функцию относительно любых двух точек структуры. При этом необходимо использовать существующие правила и методы структурных преобразований.

Дата добавления: 2017-01-29 ; просмотров: 1851 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Содержание

Классификация систем автоматического регулирования
Классификация систем автоматического регулирования
2. Математическое описание систем автоматического управления
2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
2.2. Линеаризация уравнений динамики САУ (САР)
Пример
2.3. Классический способ решения уравнений динамики
Пример
📽️ Видео

Видео:Линейные системы автоматического регулирования. Лекция 1. Классификация САУСкачать

Классификация систем автоматического регулирования

Видео:1) ТАУ (Теория автоматического управления) для чайников. Часть 1: основные понятия...Скачать

Классификация систем автоматического регулирования

Системы автоматического регулирования, применяемые в современной технике, весьма разнообразны. Быстрое расширение функционального назначения функционального назначения автоматических систем, ставшее возможным, в частности благодаря внедрению вычислительной техники, увеличивает число реализуемых классов систем. В этих условиях дать законченную подробную классификацию систем автоматического регулирования практически невозможно. Классификации, с успехом применявшиеся в недавнем прошлом, становятся в настоящее время слишком узкими, не охватывающими новых разрабатываемых и реализуемых систем.

Всякая классификация основана на определенных классификационных признаках. С точки зрения общности классификации систем автоматического регулирования наиболее удобным классификационным признаком является используемая информация об объекте регулирования. Следует отметить, что почти все автоматические системы представляют собой нелинейные устройства, которые содержат как переменные, так и распределенные параметры, в которых значение переменных в данный момент времени может зависеть не только от текущих, но и прошлых значений этих переменных.

Каждая автоматическая система характеризуется алгоритмом функционирования — совокупностью предписаний, определяющих характер изменения управляемой величины в зависимости от воздействия

В зависимости от характера изменения составляющих задающего воздействия автоматические системы разделяют на четыре класса:
— системы автоматической стабилизации, в которых задающее воздействие представляет собой постоянную величину, а регулируемая величина автоматически поддерживается неизменной при произвольном изменении нагрузки и внешних условий. Нагрузка объекта регулирования (момент нагрузки на валу электродвигателя, нагрузка гeнератора) в стабилизирующих системах обычно является основным возмущающим воздействием, наиболее резко влияющим на регулируемую величину;
— системы программного регулирования, в которых задающее воздействие и регулируемая величина изменяются по заранее заданному закону. Программную автоматическую систему можно рассматривать как систему стабилизации, в которой задача стабилизации усложняется задачей изменения регулируемой величины по заданной программе. Изменение регулируемой величины по пpoгpaммe достигается добавлением к системе некотоpoгo элемента программного устройства, изменяющего задающее воздействие во времени по заранее определенному закону;
— следящие системы предполагают изменение регулируемой величины в соответствии с изменением задающего воздействия, закон изменения которого является неизвестной функцией. Таким образом, следящая система, как и программная система, воспроизводит задающее воздействие. Однако это воздействие в следящей системе изменяется не по заранее заданной программе, а произвольно. Например, антенна радиолокатора поворачивается следуя за самолетом, траектория движения котopoгo заранее неизвестна, т. е. «следит» за ним. Отсюда происходит и название следящей системы. Задающие воздействия и регулируемые величины следящих систем могут иметь разнообразный характер по своей физической природе. Причем регулируемая величина по своей физической природе может отличаться от задающего воздействия.
— системы оптимального регулирования обеспечивают оптимальное согласно тому или иному критерию оптимальности поддержание регулируемой величины

В зависимости от того, какой математической моделью описываются процессы в автоматических системах, ониразделяют на:
— линейные автоматические системы, математическая модель которых составлена из линейных или линеаризированных дифференциальных уравнений. Если в уравнении динамики какого-либо звена линейной автоматической системы имеется хотя бы один или несколько переменных во времени коэффициентов, то получаетсялинейная автоматическая система с переменными параметрами. Если какое-либо звено описывается линейными уравнениями в частных производных, то автоматическая система будет линейной автоматической системой с распределенными параметрами. В отличие от этого обыкновенная линейная автоматическая система являетсяавтоматической системой с сосредоточенными параметрами. Если динамика какого-либо звена автоматической системы описывается линейным уравнением с запаздывающим аргументом, то автоматическая система называетсялинейной автоматической системой с запаздыванием;
— нелинейные автоматические системы, математическая модель которых составлена из нелинейных дифференциальных уравнений. К нелинейным автоматическим системам относятся все автоматические системы, в звеньях которых имеются статические характеристики любого из множества видов нелинейности. Нелинейными могут быть автоматические системы с переменными параметрами, с распределенными параметрами, с запаздыванием, импульсные и цифровые автоматические системы, если в них где-то нарушается линейность уравнения динамики.

Классификация систем автоматического регулирования

Каждая автоматическая система состоит из целого ряда звеньев, соединенных соответствующим образом между собой. Каждое отдельно взятое звено имеет вход и выход определяющих воздействие и передачу информации с одного звена на другое. В общем случае любое звено может иметь несколько входов и выходов. Входная и выходная величины могут иметь любую физическую природу.

В процессе работы автоматической системы входные и выходные величины изменяются во времени. Динамика процесса преобразования сигналов в данном звене описывается некоторым уравнением, связывающим выходную переменную со входной переменной. Совокупность уравнений и характеристик всех звеньев описывает динамику процессов управления или регулирования во всей системе в целом.

Основными признаками деления автоматических систем на большие классы по характеру внутренних динамических процессов являются следующие:
— непрерывность или дискретность динамических процессов во времени;
— линейность или нелинейность уравнений, описывающих динамику процессов регулирования.

В зависимости от характера изменения управляющих сигналов автоматические системы разделяют на три класса:
— непрерывные (аналоговые) системы, которые описываются обыкновенными дифференциальными уравнениями и в процессе регулирования структура всех связей в системе остается неизменной. Сигналы на выходе отдельных звеньев такой системы являются непрерывными функциями воздействий и времени. Между звеньями на входе и выходе автоматической системы существует непрерывная функциональная связь. При этом закон изменения выходной величины во времени может быть произвольным, в зависимости от формы изменения входной величины и от вида уравнения динамики звена. Чтобы автоматическая система в целом была непрерывной, необходимо прежде всего, чтобы статические характеристики всех звеньев были непрерывными;
— дискретные (цифровые) системы, которые описываются дифференциально-разностными уравнениями и в них через дискретные промежутки времени происходит размыкание или замыкание цепи управляющего воздействия. В дискретных системах размыкание цепи воздействия производится принудительно и периодически специальными прерывающими устройствами. Такие системы содержат импульсные элементы и осуществляют квантование сигналов как по уровню, так и по времени. Звено, преобразующее непрерывный входной сигнал в последовательность импульсов, называется импульсным. Если последующее звено автоматической системы тоже дискретное, то для него не только выходная, но и входная величины будет дискретной. К дискретным автоматическим системам относятся автоматические системы импульсного регулирования, а также автоматические системы управляющими вычислительными машинами. Эти последние дают результат вычисления на выходе дискретно, через определенные промежутки времени, в виде чисел для отдельных дискретных числовых значений выходной величины;
— релейные (дискретно-непрерывные) системы, которые описываются обоими видами уравнений. В этих системах размыкание или замыкание цепи воздействия осуществляется одним из звеньев системы при непрерывном значении входного воздействия. Размыкание или замыкание осуществляется с помощью реле или звена, имеющего релейную характеристику. Реле срабатывает при определенных значениях воздействий на его чувствительный орган. Релейные системы осуществляют квантование сигналов по времени. Статическая характеристика релейного звена имеет точки разрыва.

Каждый из этих трех классов автоматических систем разделяют на подклассы:
— стационарные автоматические системы с сосредоточенными или распределенными параметрами;
— нестационарные автоматические системы с сосредоточенными или распределенными параметрами.

При исследовании, расчете и синтезе автоматических систем нужно иметь в виду, что наиболее полно разработаны теория и различные прикладные методы для обыкновенных линейных автоматических систем. Поэтому в интересах простоты расчета всегда желательно сводить задачу к такой форме, чтобы максимально использовать методы исследования обыкновенных линейных автоматических систем. Обычно уравнения динамики всех звеньев автоматической системы стараются привести к обыкновенным линейным, и только для некоторых звеньев, где это недопустимо или где специально вводится особое линейное или нелинейное звено, учитываются эти особые их свойства.

Однако это вовсе не значит, что при проектировании новых автоматических систем нужно стремиться к обыкновенным линейным автоматическим системам. Наоборот, совершенно очевидно, что обыкновенные линейные автоматические системы обладают ограниченными возможностями. Введение особых линейных и нелинейных звеньев может придать автоматической системе лучшие качества. Особенно богатыми возможностями обладают автоматические системы со специально вводимыми нелинейностями и дискретные автоматические системы, в том числе с управляющими ЭВМ и микропроцессорные автоматические системы.

По типу и количеству сигналов системы автоматического регулирования подразделяются:
— одноконтурные системы, в которых имеется одна регулируемая величина;
— многоконтурные системы, в которых имеется несколько главных или местных обратных связей;
— системы несвязного регулирования предназначены для регулирования различных величин, не связаны друг с другом и могут взаимодействовать только через общий объект регулирования.
а) в зависимых системах несвязного регулирования изменение одной из регулируемых величин влияет на изменение других. Поэтому в таких системах процессы регулирования нельзя рассматривать изолировано друг от друга;
б) в независимых системах несвязного регулирования изменение одной из регулируемых величин не зависит от изменения остальных;
— системы связного регулирования предполагают наличие нескольких регуляторов, регулируемые величины которых имеют друг с другом взаимные связи, осуществляемые помимо объекта регулирования.

В зависимости от наличия или отсутствия ошибки регулирования САР подразделяются на:
— статические системы это такие системы, которые предполагают наличие постоянной ошибки регулирования (статизма). Характерной особенностью работы статической системы является то, что равновесие системы может быть достигнуто при различных значениях регулируемой величины и каждому значению регулируемой величинысоответствует единственное значение регулирующего органа;
— астатические системы это такие системы, которые при различных значениях внешнего воздействия на объект отклонение регулируемой величины от требуемого значения отсутствует. В таких системах равновесное состояниеимеет место при одном единственном значении регулируемой величины, равном заданному, а регулирующий органдолжен иметь возможность занимать различные положения при одном и том же значении регулируемой величины.

Видео:2) ТАУ для чайников. Часть 2.1: Математические модели...Скачать

2. Математическое описание систем автоматического управления

Публикую первую часть второй главы лекций по теории автоматического управления.
В данной статье рассматриваются:

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
2.2. Линеаризация уравнений динамики САУ (САР)
2.3. Классический способ решения уравнений динамики

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

Видео:Принципы регулированияСкачать

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях

При составлении уравнений, описывающих нестационарные процессы в САУ (САР) и которые в дальнейшем будем называть уравнениями динамики, система “разбивается” на отдельные элементы (звенья), для каждого из которых не существует проблем в записи соответствующего уравнения динамики.

На рис. 2.1.1 представлено схематичное представление САУ (звена) в переменных «вход-выход», где x(t) (или u(t)) — входное воздействие, а y(t) — выходное воздействие, соответственно. Нередко входное воздействие будет называться управляющим, а выходное воздействие — регулируемой величиной (переменной).

При составлении уравнений динамики используются фундаментальные законы сохранения из разделов “Механики”, “Физики”, “Химии” и др.

Например, при описании перемещения узла какого-то механизма силового привода используются законы сохранения: момента, энергии, импульса и др… В теплофизических (теплогидравлических) системах используются фундаментальные законы сохранения: массы (уравнение неразрывности), импульса (уравнение движения), энергии (уравнение энергии) и др

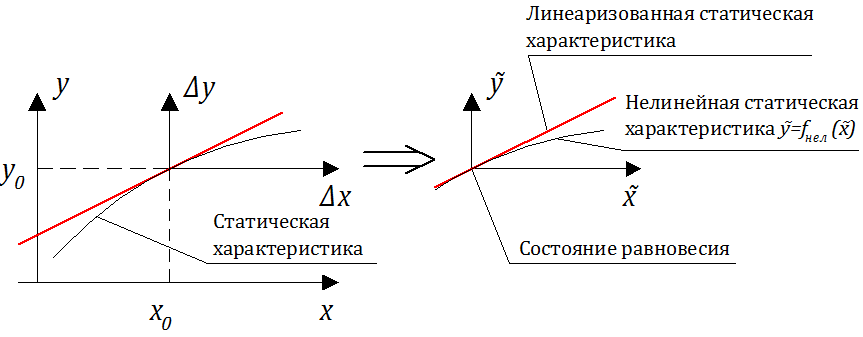
Уравнения сохранения в общем случае содержат постоянные и нестационарные члены, причем при отбрасывании нестационарных членов получают так называемые уравнения статики, которые соответствуют уравнениям равновесного состояния САУ (звена). Вычитанием из полных уравнений сохранения стационарных уравнений получают нестационарные уравнения САУ в отклонениях (от стационара).

где: — стационарные значения входного и выходного воздействий;
— отклонения от станционара, соотвесвенно.

В качестве примера рассмотрим «технологию» получения уравнений динамики для механического демпфера, схематическое изображение которого представлено на рис. 2.1.2.

Согласно 2-му закону Ньютона, ускорение тела пропорционально сумме сил, действующих на тело:

где, m — масса тела, F_j — все силы воздействующие на тело (поршень демпфера)

Подставляя в уравнение (2.1.1) все силы согласно рис. 2.2, имеем:

где — сила тяжести; — сила сопротивления пружины, — сила вязконо трения (пропорциональна скорости поршеня)

Размерности сил и коэффициентов, входящих в уравнение (2.1.2):

Предполагая, что при t ≤ 0 поршень демпфера находился в равновесии, то есть

перейдем к отклонениям от стационарного состояния:
Пусть при t>0 . Тогда, подставляя эти соотношения в уравнение (2.1.2), получаем:

если , то уравнение принимает вид:

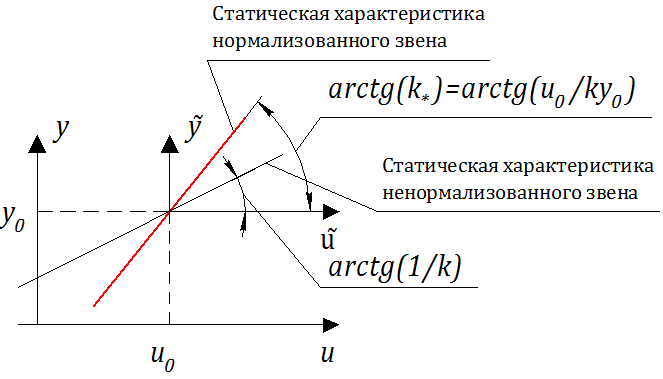
Соотношение (2.1.4) – уравнение звена (демпфера) в равновесном (стационарном) состоянии, а соотношение (2.1.5) – статическая характеристика звена – демпфера (см. рисунок 2.1.3).

Вычитая из уравнения (2.1.3) уравнение (2.1.4), получаем уравнение динамики демпфера в отклонениях:

тогда, разделив на k, имеем:

Уравнение (2.1.6) — это уравнение динамики в канонической форме, т.е. коэффициент при Δy(t) равен 1.0!

«Легко» видеть, что коэффициенты перед членами, содержащими производные, имеют смысл (и размерность!) постоянных времени. В самом деле:

Таким образом, получаем, что:
— коэффициент перед первой производной имеет размерность [c] т.е. смысл некоторой постоянной времени;
— коэффициент перед второй производной: [];
— коэффициент в правой части (): [].
Тогда уравнение (2.1.6) можно записать в операторной форме:

, что эквивалентно

где: — оператор диффренцирования;
-линейный дифференциальный оператор;
— линейный дифференциальный оператор, вырожденный в константу, равную .

Анализ уравнения (2.1.6.а) показывает, что такое уравнение имеет размерные переменные, а также размерными являются все коэффициенты уравнения. Это не всегда удобно. Кроме того, если реальная САР (САУ) состоит из многих звеньев, выходными воздействиями которых являются различные физические переменные (скорость, температура, нейтронный поток, тепловой поток и т.д.), то значения коэффициентов могут различаться на большое число порядков, что ставит серьезные математические проблемы при численном решении уравнений динамики на компьютере (поскольку числа в компьютере всегда представляются с какой-то точностью). Одним из наилучших способов избежать численных трудностей является принцип нормализации, т.е. переход к безразмерным отклонениям, которые получены нормированием отклонения на стационарное значение соответствующей переменной.

Введем новые нормированные (безразмерные) переменные:

Подставляя эти соотношения в уравнение (2.1.2), имеем:

Поддчеркнутые члены выражения в сумме дают 0 (см. 2.1.4) Перенося в левую часть члены, содержащие , и, разделив на , получаем:

где: — коэффициент усиления, причем безразмерный.

Проверим размерность коэффициента

Использованный выше «технический» прием позволяет перейти к безразмерным переменным, а также привести вид коэффициентов в уравнении динамики к легко интерпретируемому виду, т.е. к постоянным времени (в соответствующей степени) или к безразмерным коэффициентам усиления.

На рис. 2.1.4 представлены статические характеристики для механического демпфера:

Процедура нормировки отклонений позволяет привести уравнения динамики к виду:

где дифференциальные операторы.

Если дифференциальные операторы — линейные, а статическая характеристика САУ (звена) – тоже линейна, то выражение (2.1.8) соответствует линейному обыкновенному дифференциальному уравнению (ОДУ).

А если – нелинейные дифференциальные операторы, или , то уравнение динамики — нелинейное. Под нелинейными действиями понимаются все математические действия, кроме сложения (+) и вычитания (-).

Пример создания модели демпфера можно посмотереть здесь: «Технология получения уравнений динамики ТАУ»

Видео:Основы теории автоматического управленияСкачать

2.2. Линеаризация уравнений динамики САУ (САР)

Практически все реальные системы автоматического управления (САУ) являются нелинейными, причем нелинейность САУ может определяться различными причинами:

Нелинейностью статической характеристики.
Нелинейностью динамических членов в уравнениях динамики.
Наличием в САУ принципиально нелинейных звеньев.

Если в замкнутой САУ (САР) нет принципиально нелинейных звеньев, то в большинстве случаев уравнения динамики звеньев, входящих в систему, могут быть линеаризованы. Линеаризация основана на том, что в процессе регулирования (т.е. САУ с обратной связью) все регулируемые величины мало отклоняются от их программных значений (иначе система регулирования или управления не выполняла бы своей задачи).

Например, если рассмотреть управление мощностью энергетического ядерного реактора, то главная задача САР — поддержание мощности на заданном (номинальном) уровне мощности. Существующие возмущения (внутренние и внешние) “отрабатываются” САР и поэтому параметры ядерного реактора незначительно отличаются от стационарных. На рис. 2.2.1 представлена временная зависимость мощности ядерного реактора, где нормированные отклонения мощности ΔN /N₀ Рис. 2.2.1 – Пример изменения мощности реактора

Рассмотрим некоторое звено (или САР в целом), описание динамики которого можно представить в переменных “вход-выход”:

Предположим, что динамика данного звена описывается обыкновенным дифференциальным уравнением n-го порядка:

Перенесем в левую часть уравнения и запишем уравнение в виде%

где -– функция регулируемой переменной и ее производных, а также управляющего (входного) воздействия и его производных, причем F – обычно нелинейная функция.

Будем считать, что при t ≤ 0 САУ (звено) находилось в равновесии (в стационарном состоянии). Тогда уравнение (2.2.2) вырождается в уравнение статической характеристики:

Разложим левую часть уравнения (2.2.2) в ряд Тейлора в малой окрестности точки равновесного состояния .

Напомним, что разложение в ряд Тейлора трактуется следующим образом: если , то «простое» разложение функции в ряд Тейлора в окрестности точки будет выглядеть так:

C учетом вышеприведенного разложение принимает вид:

Предполагая, что отклонения выходных и входных воздействий незначительны, (т.е.:), оставим в разложении только члены первого порядка малости (линейные). Поскольку , получаем:

Подставляя соотношение (2.2.4) в уравнение (2.2.2), и перенося множители при у и u в разные части получаем уравнения:

Коэффициенты — постоянные коэффициенты, поэтому уравнения 2.2.5 — линейное дифференциальное с постоянными коэффициентами.

В дальнейшем нами будет часто использоваться операторная форма записи уравнений динамики:

где – оператор дифференцирования;
— линейный дифференциальный оператор степени n;
— линейный дифференциальный оператор степени m, причем обычно порядок оператора выше порядка оператора :

Уравнения (2.2.5) и (2.2.6) — уравнения динамики системы (звена) в отклонениях.

Если исходное уравнение (2.2.1) — дифференциальное уравнение в физических переменных (температура, скорость, поток и т.д.), то размерность коэффициентов может быть произвольной (любой).

Переход к нормализованным отклонениям позволяет “упорядочить” размерность коэффициентов. В самом деле, разделив уравнение (2.2.5) на начальные условия (значения в нулевой момент времени) и выполнив некоторые преобразования, получаем:

Приведение уравнения динамики САУ (звена) к нормализованному виду позволяет “унифицировать” размерность коэффициентов уравнений: ==>

Если вынести в правой части (2.2.7) коэффициент за общую скобку и разделить все уравнение на , то уравнение принимает вид:

или в операторном виде:

Линеаризация уравнений динамики и нормализация переменных позволяют привести уравнения динамики САУ (звена) к виду, наиболее удобному для использования классических методов анализа, т.е. к нулевым начальным условиям.

Пример

Выполнить линеаризацию уравнения динамики некоторой «абстрактной» САР в окрестности состояния (x₀, y₀), если полное уравнение динамики имеет вид:

Нелинейность полного уравнения динамики проявляется в следующем:

• во-первых, в нелинейности статической характеристики:

• во-вторых, слагаемое в левой части — чисто нелинейное, так как действие умножения является нелинейным.

Выполним процесс линеаризации исходного уравнения, динамики без разложения я ряд Тейлора, основываясь на том, что в окрестности состояния (x₀, y₀) нормированные отклонения управляющего воздействия и регулируемой величины намного меньше 1.

Преобразования выполним в следующей последовательности:

Перейдем к безразмерным переменным (нормализованным);
Выполним линеаризацию, отбросив нелинейные члены 2-го и выше порядков малости.

Перейдем к новым безразмерным переменным:

Заметим, что:
.

Подставляя значения x(t) и y(t) в исходное уравнение:

Удаляем полученного уравнения уравнения стационара: , а так же пренебрегая слагаемыми второго прядка малости: , получаем следующее уравнение:

Вводим новые обозначения:

Получаем уравнения в «почти» классическом виде:

Если в правой части вынести за общую скобку и разделить все уравнение на , то уравнение (линеаризованное) принимает вид:

Процедура нормализации позволяет более просто линеаризовать уравнение динамики, так как не требуется выполнять разложение в ряд Тейлора (хотя это и не сложно).

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

2.3. Классический способ решения уравнений динамики

Классический метод решения уравнений динамики САУ (САР) применим только для линейных или линеаризованных систем.

Рассмотрим некоторую САУ (звено), динамика которой описывается линейным дифференциальным уравнением вида:

Переходя к полной символике, имеем:

Выражение (2.3.2) — обыкновенное дифференциальное уравнение (ОДУ), точнее неоднородное ОДУ, так как правая часть ≠ 0.

Известно входное воздействие x(t), коэффициенты уравнения и начальные условия (т.е. значения переменных и производных при t = 0).

Требуется найти y(t) при известных начальных условиях.

где: — решение однородного дифференциального уравнения y_(t) $inline$ — частное решение. $inline$

Будем называть решение однородного дифференциального уравнения , собственным решением, так как его решение не зависит от входного воздействия, а полностью определяется собственными динамическими свойствами САУ (звена).

Вторую составляющую решения (2.3.3) будем называть , вынужденным, так как эта часть решения определяется внешним воздействием , поэтому САУ (САР или звено) “вынуждена отрабатывать” это воздействие:

Напомним этапы решения:

1) Если имеется уравнение вида , то сначала решаем однородное дифференциальное уравнение:

2) Записываем характеристическое уравнение:

3) Решая уравнение (2.3.5), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения
4) Тогда собственное решение записывается в виде:

если среди нет повторяющихся корней (кратность корней равна 1).

Если уравнение (2.3.5) имеет два совпадающих корня, то собственное решение имеет вид:

Если уравнение (2.3.5) имеет k совпадающих корней (кратность корней равна k), то собственное решение имеет вид:

5) Вынужденную часть решения можно найти различными способами, но наиболее распространены следующие способы:
а) По виду правой части.
б) Методом вариации постоянных.
в) Другие методы…

Если вид правой части дифференциального уравнения – относительно несложная функция времени, то предпочтительным является способ а): подбор решения. .

6) Суммируя полученные составляющие (собственную и вынужденную), имеем:

7) Используя начальные условия (t = 0), находим значения постоянных интегрирования . Обычно получается система алгебраических уравнений. Решая систему, находим значения постоянных интегрирования

Пример

Найти аналитическое выражение переходного процесса на выходе звена, если

Решение. Запишем однородное ОДУ:
Характеристическое уравнение имеет вид: ; Решая, имеем: тогда:

где — неизвестные (пока) постоянные интегрирования.

По виду временной функции в правой части запишем как:

Подставляя в исходное уравнение, имеем:

Суммируя , имеем:

Используя 1-е начальное условие (при t = 0), получаем: , а из 2-го начального условия имеем:

Решая систему уравнений относительно и , имеем:
Тогда окончательно:

Что бы проверить результ, выполним моделирование процесса в SimInTech, для этого преобразуем исходное уравнение к виду:

Создадим модель SimInTech, содержащую исходное динамическое уравнение и полученное аналитическое решение, и выведем результаты на один график (см. рис. 2.3.1).

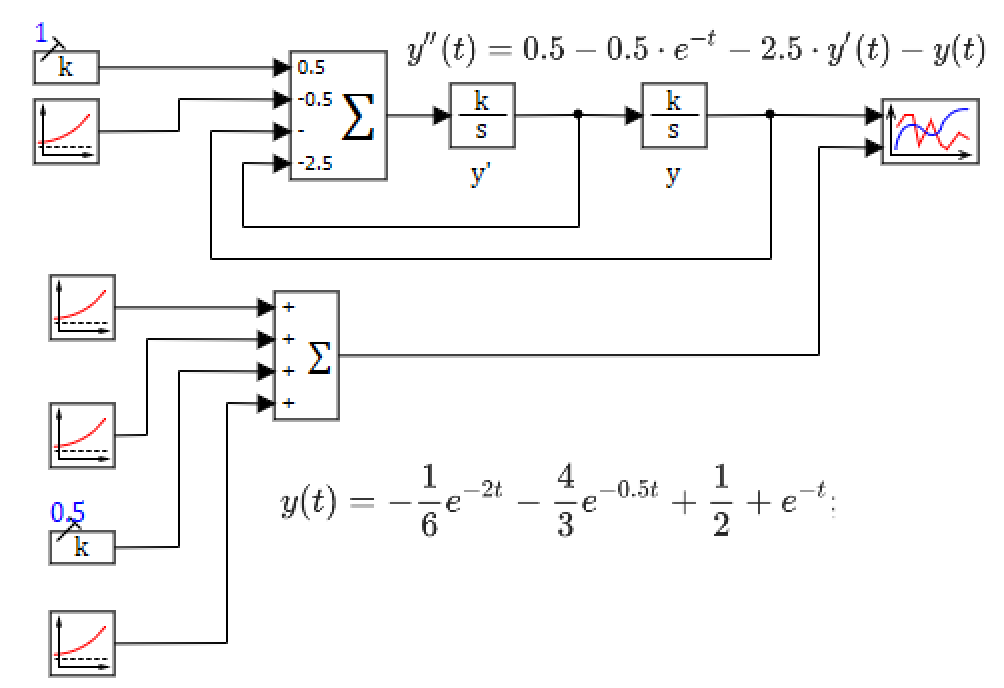
Рис. 2.3.1 – структурная схема для проверки решения

На рис. 2.3.2 приведено решение по вышеприведенному соотношению и численное решение задачи в среде SimInTech (решения совпадают и линии графиков «наложены» друг на друга).