Практическая работа № 1
Физические величины. Применение теории размерностей
Цель работы: научить студентов пользоваться международной системой физических единиц и приобрести практические навыки применения теории размерностей.
Характер выполнения работы: каждый студент выполняет работу индивидуально.
Общепринятые или установленные законодательным путём характеристики (меры) различных свойств, общих в качественном отношении для многих физических объектов (физических систем, их состояний и происходящих в них процессов), но в количественном отношении индивидуальных для каждого из них, называются физическими величинами.
Таким образом, под термином «физическая величина» понимают свойство, общее в качественном отношении многим физическим объектам, но в количественном отношении индивидуальное для каждого из них.
Количественным выражением этого свойства в объекте является размер физической величины, а числовой оценкой её размера – значение физической величины. Физическая величина, которой по определению присвоено числовое значение, равное единице, называют единицей физической величины.
В любой системе единиц существует лишь одна основная единица данной физической величины.
Международная система единиц (СИ) была принята в 1960г. на XI генеральной конференции по мерам и весам. В нашей стране данная система введена в действие с 1 января 1982г., в соответствии с ГОСТ 8.417 – 81 «ГСИ. Единицы физических величин».
В настоящее время она характеризуется как когерентная система единиц, состоящая из семи основных, двух дополнительных и ряда производных единиц, число которых не ограничено.
Основные и дополнительные единицы СИ приведены в табл. 1.
Производные единицы Международной системы единиц образуются из основных и дополнительных единиц СИ на основании законов, устанавливающих связь между физическими величинами, или уравнений по которым определяют физическую величину.
Единицы могут быть дольными и кратными от единиц СИ.
Кратной единицей называют единицу, которая в целое число раз больше системной или внесистемной единицы.
Дольной единицей называют единицу, которая в целое число раз меньше системной или внесистемной единицы.
Единицы физических величин СИ
Основные
Сила электрического тока
радиан
Все приставки пишутся слитно с наименованием основной единицы, к которой они присоединяются (килограмм, миллиметр). Присоединение двух и более приставок не допускается.
Для образования наименьших кратных и дольных единиц физических величин используют приставки изложенные в табл. 2.
Качественной характеристикой измеряемых величин является их размерность. Она отражает её связь с основными величинами и зависит от выбора последних.
Размерность обозначается символом dim, происходящим от слова dimension, которое в зависимости от контекста может переводится как размер, и как размерность.
Размерность основных физических величин обозначается соответствующими заглавными буквами. Для длины, массы, времени, например dim l = L; dim m = M; dim t = T.
Множители и приставки для образования десятичных
кратных и дольных единиц и их наименований
Множитель
от какого слова
из какого языка
шесть раз по 103
пять раз по 103
При определении размерности производных величин руководствуются следующими правилами:
1. Размерность левой и правой части не могут не совпадать так как сравниваться между собой могут только одинаковые свойства, объединяя левые и правые части уравнений, отсюда можно прийти к выводу, что алгебраически суммироваться могут только величины, имеющие одинаковые размерности.
2. Алгебра размерностей мультипликативна, т. е. состоит из одного единственного действия – умножения.
2.1. Размерность произведения нескольких величин равна произведению их размерностей. Так, если зависимость между значениями величин Q, A, B, C имеет вид Q = A 

dim Q = dim A 

2.2. Размерность частного при делении одной величины на другую равна отношению их размерностей, Q = A/B, то
dim Q = dim A/dim B
2.3. Размерность любой величины, возведённой в некоторую степень, равна её размерности в той же степени, так, если
dim Q = 
Например, если скорость определять по формуле V = l/t, то
dim V = dim l/dim t = L/T = LT-1
Если сила по второму закону Ньютона F = m 
dim F = dim m 
Таким образом, всегда можно выразить размерность производной физической величины за размерность основных физических величин с помощью степенного одночлена dim Q = Lб 

Порядок выполнения работы
В начале занятия студенты должны охарактеризовать общие правила конструирования систем единиц. Далее следует ознакомиться с основными и производными единицами системы СИ, с правилами написания обозначений единиц:
— обозначения единиц ставят после их числовых значений и помещают в строку с ними;
— в обозначениях единиц точку и знак сокращения не ставят;
— в буквенных обозначениях отношений единиц в качестве знака деления должна применяться только одна черта: косая или прямая. При применении косой черты обозначения единиц в числителе и знаменателе помещают в строку, произведение обозначений единиц в знаменателе заключают в скобки, например, Вт/(м2·К). Допускается вместо знака черты применять обозначения единиц в виде произведений единиц, возведённых в степени 
Затем студенты должны ознакомиться с принципом образования наименьших кратных и дольных единиц.
В конце занятия следует выполнить ряд заданий, представленных преподавателем по применению теории размерностей, ответить на вопросы, касающиеся данной темы. Оформить отчёт.
Для проверки качества усвоения материала по теории размерностей рекомендуется выполнить следующие задания.
По определяющим уравнениям выразить размерности физических величин:
ускорение a = V/t;
плотность с = m·V;
По размерности физических величин определить основные формулы и обозначить единицы измерений:
удельный вес L3M-1;
динамическая вязкость L-1MT-1;
поверхностное натяжение MT-2;
магнитная проводимость L2MT-2I-2;
удельное электрическое сопротивление L3MT-2I-2;
1.Каковы правила конструирования систем единиц?
2.Назовите основные и дополнительные единицы системы СИ?
3.Как образуются кратные и дольные единицы Международной системы единиц?
4.Что называют единицей физической величины?
5.Принципы образования производных единиц Международной системы?
6.Что такое физическая величина?
7.Что такое размер физической величины?
8.Какие единицы являются дольными, кратными от единиц СИ?
9.Что такое системные, внесистемные единицы?
10.Какие существуют правила написания обозначения единиц?
ГОСТ 8.417.-81. ГСИ. Единицы физических величин.
2. Коротков , стандартизация и сертификация [Электронный ресурс]: учебное пособие/ , — Электрон. текстовые данные.— Томск: Томский политехнический университет, 2015.— 187 c.
Видео:Физические величины и их измерения. 7 класс.Скачать

Применение размерности для проверки правильности решения физических задач
Разделы: Физика
Цели:
- шире использовать полученные теоретические знания по физике;
- вооружить учащихся большим набором способов решения задач.
1. Понятие размерности
Для начала упорядочим некоторые понятия, с которыми мы имели дело раньше и с теми, которые встретятся нам в будущем. К таким физическим понятиям относятся: наименование, название физической величины, в выбранной системе единиц, размерность, обозначение и определяющее уравнение.
Разберём это на некоторых примерах взятых из раздела «Механика» и знакомых нам. Для краткости сведём всё это в таблицу.
| Название физ. величины | Обозначение | Определяющее уравнение | Размерность |
| Площадь | |||
| Объём | |||
| Скорость | |||
| Ускорение | |||
| Плотность |
Это простые и часто встречающиеся понятия, причём название физической величины вытекает из определяющего её уравнения. Но ряд физических величин имеют «клички». Название величины не следует прямо, как прежде, из определяющего уравнения.
Наименование величины – сила. Название единицы измерения – Ньютон. Вспомним материал 7-го класса. Что такое Ньютон? Это такая сила, которая за 1 секунду изменяет скорость тела массой 1 кг на 1 метр в секунду. Примером одной из сил является вес тела. Мы знаем, что вес тела равен Р = mg, где m – масса тела , а g – ускорение свободного падения.
Из физики 8-го класса мы знаем, что ускорение измеряется в м/с 2 . Значит, если речь идёт о весе тела Р, то он равен произведению массы тела на ускорение. Отсюда можно сделать вывод, что и любая другая сила F равна произведению массы тела на полученное в результате действия силы ускорение, т.е. F = ma.
Обратим внимание на то, что, если масса тела равна 1 кг и полученное ускорение равно 1 м/с 2 , то и сила будет равна единице силы, то есть 1-му Ньютону. Тогда размерность Ньютона будет
[ F ] = кг 
Каждой такой единице присуща ей размерность, которая показывает, из каких основных единиц системы СИ «приготовлена», «сделана» такая единица, в какой степени входят в состав этой величины основные единицы и где они находятся в числителе или в знаменателе.
Что такое определяющее уравнение? Это уравнение, которое следует из определения физической величины.
1. Скорость – это физическая величина равная отношению пути, пройденного телом, ко времени за которое этот путь пройден. Отсюда следует определяющее уравнение V = S/t.
2. Работа – это физическая величина равная произведению силы, приложенной к телу на путь, который прошло тело под действием этой силы. Отсюда следует определяющее уравнение: A = F S.
До введения интернациональной системы единиц (СИ), существовал несколько систем единиц.
Так в одной из них основными единицами были: единица массы – грамм; единица длины – сантиметр; единица времени – секунда. Эта система единиц называлась СГС.
Были и другие системы единиц. Но масса есть масса в любой системе. Будь она в кг, или в г, или в мг. Поэтому, независимо от выбранной системы единиц, принято размерность выражать в символах. Масса – М. Длина – L. Время – Т.
В таблице выше соответствующая колонка называется просто размерность.
Задачи для самостоятельного решения.
1. Определить размерность Джоуля. Определяющее уравнение A = F S
2. Определить размерность Ватта. Определяющее уравнение N = A / t
3. Определить размерность Герца. Определяющее уравнение 
4. Определить размерность Паскаля. Определяющее уравнение р = F/S
5. Определить размерность момента силы. Определяющее уравнение М = F L.
2. Проверка правильности решения задач по размерности
«Видкиль воно взялось и на щоб воно сдалось» Украинская пословица.
Откуда взялась размерность мы рассмотрели. Рассмотрим где, и как она может быть применена и её особенности.
Рассмотрим решение нескольких задач:
1. Определить расстояние между Землёй и Солнцем, если луч света, двигаясь со скоростью 3 х 108 м/с, проходит это расстояние примерно за 8,5 минут?
2. Какое расстояние по прямой может пройти ракета за 1 минуту, двигаясь от места старта с ускорением 20 м/с 2 ?
3. Автомобиль, двигаясь со скоростью 54 км/ч, пошел на обгон и в течение 10 секунд двигался с ускорением 2 м/с 2 . Какой путь прошел автомобиль за это время?
4. Автомобиль, двигаясь со скоростью 54 км/ч, перед поворотом в течение 10 секунд двигался равнозамедленно с ускорением – 2 м/с 2 . Какой путь прошел автомобиль за это время?
Проанализируем решение этих задач.
1. Что общего было в этих задачах? (Определялся путь S)
2. В чём различие в этих задачах? (В каждой задаче описывается различное движение, а значит, применяются различные уравнения для определения пути)
То есть различие в том, что одна и та же величина (путь) определяется через различные величины. В № 1 через V и t. В № 2 через а и t. В № 3 и № 4 через Vо, a, t.
Эти величины имеют различные размерности, а в результате произведенных действий получается во всех случаях одна и та же размерность – метр.
Произведём, не используя модулей этих величин, предлагаемые действия только с размерностями.
1. S = V t = 




Отсюда следует закономерность: В правильно составленном уравнении, размерность правой его части равна размерности его левой части.
Эту закономерность можно применить для проверки правильности решения задач.
Допустим, задачу №3 решили с ошибкой (она очень часто встречается), записав
уравнение так S = Vо + at 2 /2 , тогда S = 15 + 2 х 10 2 /2 = 65 (м). Так как правильный ответ неизвестен, то неясно, как проверить правильность решения, и найти причину ошибки.
То ли ошибка в вычислениях, то ли в преобразованиях, то ли в неправильном написании правильно выбранного уравнения?
Проверяя правильность решения по наименованию можно найти причину ошибки.
Как это сделать? Вместо модулей величин подставить размерности величин и сравнить размерности левой и правой части уравнения. (использовать, указанную выше, закономерность )
Отсюда следует, L =/= 1 + Т. Задача решена неверно. Где ошибка? В правой части уравнение представляет двучлен. Одна его часть имеет размерность L, а другая L/T. Как из этого выражения L/T получить L? Нужно умножить его на Т. Тогда получим размерность первого члена L. Первый член и второй член правой части уравнения будут иметь размерность L, то есть L + L = L. Левая и правая части будут иметь одинаковую размерность. Значит, первый член правой части уравнения должен иметь вид не Vо, а Vо t.
Теперь, предположим, решающий допустил другую ошибку. В уравнении S = Vоt +at 2 /2 вместо знака «+» поставил знак «–». Поможет ли здесь метод размерности указать на ошибку? Решение задачи № 4 говорит о том, что задача решена правильно. L = L – L = L, но модуль величины другой.
Отсюда следует второй вывод: метод размерностей может подсказать ошибочность физического направления решения, но не может подсказать ошибочность математического действия.
Решим несколько задач по кинематике и сделаем проверку их правильности решения, применив метод размерности.
Задача № 1.
За время равное 2 с, тело, двигаясь прямолинейно и равноускоренно, прошло путь 20 м. Его скорость при этом увеличилась в 3 раза. Определить ускорение тела.
Сделаем проверку решения методом размерности. 
Размерности левой и правой части уравнения совпадают, значит, задача решена правильно.
Задача №2.
Тело, двигаясь от остановки равноускоренно, за первые 5 секунд движения прошло путь 10 м. Какой путь пройдёт это тело за 10 секунд от начала движения?
Задача № 3. Тело, двигаясь равноускоренно, за 5 секунд движения прошло путь 100 м , а за 10 сек. – 300 м. Определить начальную скорость движения тела.
Мы проделали громоздкие преобразования. Не допустили ли мы ошибку? Воспользуемся знанием закономерности размерности и проверим свою работу.
L T–1 = 
Подставим числовое значение входящих величин и получим числовой ответ задачи.
V0 = 
Задача №4. Во сколько раз скорость пули при вылете её из ствола винтовки больше скорости этой пули при прохождении ею 1/3 ствола?
Видео:Урок 3 (осн). Физические величины и единицы их измеренияСкачать

Тема: Основные, производные и внесистемные единицы системы единиц СИ
Практическая работа № 1
Цель работы:
1. Изучить единицы системы СИ, научиться выявлять зависимости между производными и основными единицами СИ.
2. Научиться приводить несистемные единицы физических величин в системные в соответствии с международной системой единиц СИ
Задание.
Задание 1: Для каждой единицы измерений своего варианта выведите взаимосвязь производной единицы с основными единицами СИ.
Задание 2: По определяющим уравнениям выразить размерности физических величин
Задание 3: Переведите величины с использованием кратных, дольных и внесистемных величин в единицы системы СИ.
Задание 4: Переведите указанные древнерусские величины в систему СИ.
Задание 5: Переведите иностранные единицы измерения в систему СИ.
| № варианта | Задание 1 | Задание 2 | Задание 3 | Задание 4 | Задание 5 |
| Сименс | работа A = F·l | 89 мкм | 21 четверть | 32 кв. фута | |
| Кулон | мощность P = A/t | 20 мин | 5 четвертей | 58 ст. ложки | |
| Ом | Напряжение U = R . I | 10 дм | 61 золотник | 71 стоун | |
| Беккерель | сила F = m·a | 201 л | 91 лот | 78 миль | |
| Люмен | мощность P = A/t | 50 т | 27 долей | 120 ч. Ложки | |
| Джоуль | скорость V = l/t | 8 мА | 41 бочка | 90 амер. барреля | |
| Генри | ускорение a = V/t | 200 пФ | 6 осьмин | 55 кв. мили | |
| Паскаль | плотность ρ = m·V | 81 сут | 5 пудов | 41 фунт | |
| Герц | сила F = m·a | 149 г | 21 куб. фут | 405 ярдов | |
| Грей | давление P = F/S | 1 МБ | 25 миль | 122 морские мили | |
| Вольт | Сопротивление R = U/I | 1830 мм | 21 кв. десятина | 5 кварт | |
| Вебер | плотность ρ = m·V | 12 мВ | 71 шкалик | 54 кв. дюйма | |
| Тесла | работа A = F·l | 10 дал | 12 аршин | 21 бушель | |
| Фарад | сила F = m·a | 200 км | 31 гранец | 6 центнеров США | |
| Люкс | плотность ρ = m·V | 89см | 6 верст | 61 галлон | |
| Ватт | ускорение a = V/t | 653 ТБ | 56 фунтов | 45 акров | |
| Кулон | Напряжение U = R . I | 6 ГБ | 31 четверик | 81 унция | |
| Герц | давление P = F/S | 5 мА | 151 вершок | 48 анг. Баррелей | |
| Джоуль | работа A = F·l | 456 кДж | 5 кв. аршин | 51 стакан | |
| Паскаль | мощность P = A/t | 50 мкм | 61 штоф | 56 англ. Барреля | |
| Тесла | давление P = F/S | 25 мВ | 10 дюймов | 501 фарлонг | |
| Ньютон | скорость V = l/t | 3 ч | 20 футов | 25 дюймов | |
| Вольт | Сопротивление R = U/I | 1962 нм | 2 сажени | 22 куб. мили | |
| Зиверт | скорость V = l/t | 26 0 | 9 ведер | 302 фута | |
| Ватт | Напряжение U = R . I | 65га / | 4 кв. дюйма | 36 пек | |
| Тесла | ускорение a = V/t | 10 см | 81 берковец | 27 амер. баррелей |
Оборудование, наглядные пособия: таблицы систем единиц СИ, внесистемных единиц, калькулятор
Теоретические основы:
Метрология – наука об измерениях, методах и средствах обеспечения их единства и требуемой точности.
Объектами метрологии являются физические и нефизические величины.
Величина— это состояние, характеристика, сущность какого-либо объекта (материала, тела, системы и т.д.), а физическая величина — состояние, характеристика, сущность физических свойств объекта. Единицей физической величины является принятая (договорная) количественная доля физического свойства объекта (1 кг — 1 единица, 2 кг — 2 единицы).
Измерение— это определение количества единиц данной физической величины.
Характеристиками физических величин являются размер, т. е. количество единиц физической величины в данном объекте, обнаруженное измерительными испытаниями, и размерность— выражение, связывающее измеряемую величину с основными единицами системы измерений при коэффициенте пропорциональности, равном единице. Размерность имеет национальное или международное буквенное написание с учетом масштаба. Физическая величина может иметь безусловное (т — масса) или условное, т. е. не входящее в обязательное применение (n — число студентов), буквенное обозначение. Любое измеренное значение состоит из размера, размерности, указания масштаба и обозначения физической величины.
Потребность в измерениях возникла в древние времена. Людям требовалось производить равноценный обмен товаров, накапливать и передавать информацию об инженерных военных сооружениях. Для измерений использовались подручные объекты природного происхождения: горошина боба (
0,2 г) – единица карат; зерно (
0,062 г) – гран, единица аптекарского веса. Многие меры были связанны с размером тела человека: вершок – длина фаланги указательного пальца; локоть; сажень – расстояние, до которого может дотянуться человек и пр. Эти природные объекты сильно отличались друг от друга и не обеспечивали требуемую точность. Возникла необходимость в создании образцовых мер – объектов, по которым люди сверяли свои средства измерения, брали мерку. Каждая страна разрабатывала свои образцовые меры и устанавливала свои единицы измерения. Такое положение дел затрудняло развитие Международной торговли и обмен технической информацией, так как отношение между мерами в различных странах не всегда можно было определить точно. Возникла потребность в Международной системе мер. В 1875 г. Россия подписала Метрическую конвенцию в Париже, которая была призвана снять эти барьеры. Были начаты работы по разработке Международных эталонов метра и килограмма. В последующие годы была принята система СГС (сантиметр, грамм, секунда), были введены базовые единицы в области электротехники и оптики.
В 1960 г. на IX Международной конференции по мерам и весам был принят стандарт, который получил название «Международная система единиц (СИ)».
Сейчас в РФ применение СИ закреплено в межгосударственном стандарте ГОСТ 8.417 – 2002 «Государственная система обеспечения единства измерений. Единицы величин».
В систему СИ входят семь основных единиц физических величин (Таблица 1), т.е. конкретных единиц, имеющих эталоны, две дополнительные (радиан – плоский угол и стерадиан – телесный угол), производные, кратные, дольные.
Эталон единицы физической величины — это законодательно установленное количество физического свойства объекта, выраженное в практически неизменных долях другой физической величины. Так как эталоны основных единиц носят договорный характер, их определения уточняются по мере развития науки и техники.
Единицы измерений являются одним из объектов Закона РФ «Об обеспечении единства измерения» (ст. 8) в котором регулируется допуск к применению единиц величин Международной системы единиц. Наименования, обозначения и правила написания единиц величин, а также правила их применения на территории РФ устанавливает Правительство РФ, за исключением случаев, предусмотренных актами законодательства РФ.
Правительством могут быть допущены к применению наравне с единицами величин Международной системы единиц внесистемные единицы величин. Например, в России такими внесистемными единицами измерений являются градус Цельсия и ккал, наряду с Кельвином и джоулем.
Производные единицы физических величин, входящих в систему СИ, — это обязательные единицы, которые могут быть выражены через основные, как правило, образуют с помощью простейших уравнений связи между величинами (определяющих уравнений), в которых числовые коэффициенты равны 1. Для образования производных единиц обозначения величин в уравнениях связи заменяют обозначениями единиц СИ (Таблица 2)
Кратная единица – единица физической величины, в целое число раз большая системной или внесистемной единицы. Множители и приставки, используемые для образования кратных единиц, приведены в таблице 3.
Дольная единица – единица физической величины, в целое число раз меньше системной или внесистемной единицы. Множители и приставки, используемые для образования дольных единиц, приведены в таблице 3.
Внесистемная единица – это единица физической величины, не входящая ни в одну из принятых систем единиц. Внесистемные единицы по отношению к единицам СИ разделяют на четыре вида:
1. Единицы, допускаемые к применению наравне с единицами СИ (Таблица4).
2. Единицы, допускаемые к применению в специальных областях, например: астрономическая единица, парсек, световой год — единицы длины в астрономии; электрон-вольт — единица энергии в физике и т.д.
3. Единицы, временно допускаемые к применению наравне с единицами СИ, например: морская миля в морской навигации, карат в ювелирном деле и др.
В соответствии с международным соглашением эти единицы должны изыматься из употребления.
4. Единицы, изъятые из употребления, например: единица мощности — лошадиная сила; единица давления — миллиметр ртутного столба и др.
Порядок проведения работы:
В начале занятия студенты должны охарактеризовать общие правила конструирования систем единиц. Далее следует ознакомиться с основными и производными единицами системы СИ, с правилами написания обозначений единиц:
— обозначения единиц ставят после их числовых значений и помещают в строку с ними;
— в обозначениях единиц точку и знак сокращения не ставят;
— в буквенных обозначениях отношений единиц в качестве знака деления должна применятся только одна черта: косая или прямая.
При применении косой черты обозначения единиц в числителе и знаменателе помещают в строку, произведение обозначений единиц в знаменателе заключают в скобки, например, Вт/(м 2 ·К). Допускается вместо знака черты применять обозначения единиц в виде произведений единиц, возведённых в степени; Вт·м -2 ·К -1 .
Пример. Производная единица Ньютон (Н) – сила, изменяющая за 1 с скорость тела массой 1 кг на 1 м/с в направлении действия силы. Числовое значение силы можно определить с помощью второго закона Ньютона
где m – масса мела, кг; а – ускорение тела, вызванное приложенной силой, м/с 2 . Заменим обозначения величин в формуле (3) обозначениями единиц СИ
Н = (кг ∙ м)/с 2 = кг∙м с -2 (2)
Уравнение (2) показывает связь производной единицы Н с основными единицами СИ.
мощность P = A/t Вт = Дж/с = кг×м 2 /c
Затем студенты должны ознакомится с принципом образования кратных и дольных единиц.
120 мкм = 120 ∙ 10 -6 м
Следующим заданием является ознакомление с Русской системой мер и системами мер других стран.
21 куб. фут = 46656куб. дюймам = 764556,5376 куб. см = 0,7645565376 куб. м
20 амер. баррелей= 2384 литров = 2,384 м 3
| Задание | Ответ |
| 1. | кг∙м с -2 |
| 2. | Дж/с = кг×м 2 /c |
| 3. | 120 ∙ 10 -6 м |
| 4. | 0,7645565376 куб. м |
| 5. | 2,384 м 3 |
В конце занятия следует выполнить ряд заданий, представленных преподавателем, ответить на вопросы, касающиеся данной темы. Оформить отчёт.
В соответствии с заданием, указанным в таблице 1, используя таблицы 2-7 записать отчет.
Основные единицы системы СИ Таблица1
| Наименование физических величин | Единица | |||
| наименование | условное обозначение | наименование | обозначение | |
| международное | русское | |||
| Основные | ||||
| Длина | L | метр | M | м |
| Масса | M | килограмм | Rg | кг |
| Время | T | секунда | S | с |
| Сила электрического тока | I | ампер | A | А |
| Термодинамическая температура | Q | кельвин | K | К |
| Количество вещества | N | моль | mol | моль |
| Сила света | J | канделла | rd | кд |
Производные единицыТаблица2
| Величина | Единица измерения | Обозначение | Выражение | ||
| русское название | международное название | русское | международное | ||
| Плоский угол | радиан | radian | рад | rad | м×м -1 = 1 |
| Телесный угол | стерадиан | steradian | ср | sr | м 2 ×м -2 = 1 |
| Частота | герц | hertz | Гц | Hz | с -1 |
| Сила | ньютон | newton | Н | N | кг×м/c 2 |
| Энергия | джоуль | joule | Дж | J | Н×м = кг×м 2 /c 2 |
| Мощность | ватт | watt | Вт | W | Дж/с = кг×м 2 /c 3 |
| Давление | паскаль | pascal | Па | Pa | Н/м 2 = кг*м -1 с 2 |
| Световой поток | люмен | lumen | лм | lm | кд×ср |
| Освещённость | люкс | lux | лк | lx | кд×ср×м -2 |
| Электрический заряд | кулон | coulomb | Кл | C | А×с |
| Электрическое напряжение, | вольт | volt | В | V | кг×м 2 ×с -3 ×А -1 |
| Сопротивление | ом | ohm | Ом | Ω | кг×м 2 ×с -3 ×А -2 |
| Ёмкость | фарад | farad | Ф | F | кг -1 ×м -2 ×с 4 ×А 2 |
| Магнитный поток | вебер | weber | Вб | Wb | кг×м 2 ×с -2 ×А -1 |
| Магнитная индукция | тесла | tesla | Тл | T | кг×с -2 ×А -1 |
| Индуктивность | генри | henry | Гн | H | кг×м 2 ×с -2 ×А -2 |
| Электрическая проводимость | сименс | siemens | См | S | кг -1 ×м -2 ×с 3 А 2 |
| Радиоактивность | беккерель | becquerel | Бк | Bq | с -1 |
| Поглощённая доза ионизирующего излучения | грэй | gray | Гр | Gy | Дж/кг = м 2 /c 2 |
| Эффективная доза ионизирующего излучения | зиверт | sievert | Зв | Sv | Дж/кг = м 2 /c 2 |
Кратные и дольные единицы системы СИ Таблица3
| Десятичный множитель | Приставка | Единицы | ||||
| Наименование | Происхождение | Обозначение | ||||
| от какого слова | из какого языка | Междуна-родное | русское | |||
| 1000000000000000000=10 18 | экса | шесть раз по 10 3 | греч. | E | Э | кратные |
| 1000000000000000=10 15 | пета | пять раз по 10 3 | греч. | P | П | |
| 1000000000000=10 12 | тера | огромный | греч. | T | Т | |
| 1000000000=10 9 | гига | гигант | греч. | G | Г | |
| 1000000=10 6 | мега | большой | греч. | M | М | |
| 1000=10 3 | кило | тысяча | греч. | k | к | |
| 100=10 2 | гекто | сто | греч. | h | г | |
| 10=10 1 | дека | десять | греч. | da | да | |
| 0,1=10 -1 | деци | десять | лат. | d | д | дольные |
| 0,01=10 -2 | санти | сто | лат. | c | с | |
| 0,001=10 -3 | милли | тысяча | лат. | m | м | |
| 0,000001=10 -6 | микро | малый | греч. | μ | мк | |
| 0,000000001=10 -9 | нано | карлик | лат. | n | н | |
| 0,000000000001=10 -12 | пико | пикколо | итал. | p | п | |
| 0,000000000000001=10 -15 | фемто | пятнадцать | дат. | f | ф | |
| 0,000000000000000001=10 -18 | атто | восемнадцать | дат. | a | а |
Внесистемные единицы системы СИ Таблица4
| Наименование величины | Единица | ||
| Наименование | Обозначение | Соотношение с единицей СИ | |
| Масса | Тонна | т | 10 3 кг |
| Атомная единица массы | а.е.м. | 1,66057٠10 -27 кг | |
| Время | Минута | мин | 60 с |
| Час | ч | 3600 с | |
| Сутки | сут | 86400 с | |
| Плоский угол | Градус | … 0 | (π/180)рад = 1,745329…٠10 -2 рад |
| Минута | … / | (π/10800)рад = 2,908882…٠10 -4 рад | |
| Секунда | … // | (π/648000)рад = 40848137…٠10 -6 рад | |
| Объем | Литр | л | 10 -3 м 3 |
| Длина | Астрономическая единица | А.е. | 1,45598٠10 11 м (приблизительно) |
| Парсек | пк | 3,0857٠10 16 м (приблизительно) | |
| Световой год | св.год | 9,4605٠10 15 м | |
| Оптическая сила | Диоптрия | дптр | 1 м -1 |
| Площадь | Гектар | га | 104 м 2 |
| Энергия | Электрон-вольт | эВ | 1,60219٠10 -19 Дж |
| Полная мощность | Вольт-ампер | В٠А | — |
| Реактивная мощность | Вар | вар | — |
Русская система мер
Меры длины
1 миля = 7 верстам = 7,4676 км
1 верста = 500 саженям = 1,0668 км
1 сажень = 3 аршинам = 7 футам = 2,1336 м
1 аршин = 16 вершкам = 28 дюймам = 0,7112 м
1 вершок = 1,75 дюйма = 44,45 мм
1 фут = 12 дюймам = 0,3048 м
1 дюйм = 10 линиям = 25,4 мм
1 линия = 10 точкам = 2,54 мм
1 точка = 1/1200 фута
Меры площади
1 кв. верста = 250 000 кв. саженей = 1,1381 кв. км
1 кв. десятина = 2400 кв. саженям = 1,0925 га
1 кв. сажень = 9 кв. аршинам = 49 кв. футам = 4,5522 кв. м
1 кв. аршин = 256 кв. вершкам = 784 кв. дюймам = 0,0929 кв. м
1 кв. дюйм = 100 кв. линиям = 6,4516 кв. см
Меры объема тел
1 куб. сажень = 27 куб. аршинам = 343 куб. футам = 9,7127 куб. м
1 куб аршин = 4096 куб. вершкам = 21952 куб. дюймам
1 куб вершок = 5,3594 куб. дюймам = 87,8244 куб. см
1 куб. фут = 1728 куб. дюймам
1 куб. дюйм = 1000 куб. линий = 16,3871 куб. см
Меры сыпучих тел
1 четверть = 2 осьминам = 8 четверикам = 209,91 л
1 осьмина = 4 четверикам = 104,95 л
1 четверик = 8 гарнцам = 26,239 л
1 гарнец = 1/8 четверика = 3,2798 л
Меры жидких тел
1 бочка = 40 ведрам = 491,96 л
1 ведро = 4 четвертям = 10 штофам = 12,299 л
1 четверть = 2,5 штофа = 5 водочным бутылкам = 3,0748 л
1 штоф (кружка) = 2 водочным бутылкам = 10 чаркам = 1,2299 л
1 винная бутылка = 1/16 ведра = 0,7687 л
1 водочная или пивная бутылка = 1/20 ведра = 5 чаркам = 0,615 л
1 чарка = 1/100 ведра = 2 шкаликам = 122,99 мл
1 шкалик = 1/200 ведра = 61,5 мл
Меры массы (веса)
1 берковец = 10 пудам = 1,63805 ц
1 пуд = 40 фунтам = 16,3805 кг
1 фунт = 32 лотам = 96 золотникам = 409,51241 г
1 лот = 3 золотникам = 12,797 г
1 золотник = 96 долям = 4,266 г
1 доля = 44,43 мг
Система мер иностранных государствТаблица 6
| Меры сыпучих тел | |
| Британские | Метрические |
| 1 quart (кварта) | 1,1012 литра |
| 1 peck (pk) (пек) | 8,8098 литров |
| 1 bushel (bu) (бушель) | 35,239 литров |
| Англо-американские | Метрические |
| 1 cubicinch (куб. дюйм) | 16,387 куб. см |
| 1 cubicfoot (куб. фут)= 1728 куб. дюйм | 0,028317 куб. м |
| 1 cubicyard (куб. ярд)= 27 куб. фут | 0,76455 куб. м |
| 1 cubicmile (куб. миля) | 4,16818 куб. км |
| Меры жидкостей | |
| Англо-американские | |
| 1 gallon (галлон) | 4 quarts (кварта) |
| 1 gallon (галлон) | 16 cups (стакан) |
| 1 cup (стакан) | 16 tablespoons (столовая ложка) =48 teaspoons (чайная ложка) |
| 1 teaspoon (ч. ложка) | 4,9 миллилитров |
| 1 (английский) баррель | 4,5 бушеля = 163,66 литров |
| 1 американский баррель | 31,5 амер. галлонов = 119,2 литров |
| 1 tablespoon (ст. ложка) | 14,8 миллилитров |
| 1 cup (стакан) | 236 миллилитров |
| Меры площади | |
| Англо-американские | Метрические |
| 1 squareinch (кв. дюйм) | 645,16 кв. мм=6,4516 кв. см |
| 1 squarefoot (кв. фут) | 929,03 кв. см=0,0929 кв. м |
| 1 squareyard (кв. ярд) | 0,83613 кв. м |
| 1 acre (акр) | 4047 кв. м=0,4047 гектара |
| 1 squaremile (кв. миля) | 2,5890 кв. км |
| Меры веса | |
| Английская система меры веса(для всех товаров, кроме благородных металлов,драгоценных камней и лекарств), (Avoirdupois) | Метрическая |
| 1 унция(oz) | 28,350 гр |
| 1 фунт | 0,4536 кг |
| 1 стоун | 6,350 кг |
| 1 центнер (Брит.) | 50,6 кг |
| 1 центнер (США) | 45,3 кг |
| 1 центнер (Россия) | 100 кг |
| 1 короткая тонна | 907,18 кг |
| 1 длинная тонна | 1016 кг |
| Линейные меры | |
| Англо-американские | Метрические |
| 1 foot (фут) | 30,48 см=12 дюймов=0,3048 м |
| 1 yard (ярд) | 0,9144 м=36 дюймов=91,44 см З фута |
| 1 furlonq (фарлонг) | 0,2011 км=220 ярдов=201,17 м |
| 1 mile (миля) | 1760 ярдов=8 фарлонгов |
| 1 naut. mile (морская миля) | 1,832 км= 832,0 м =6080 футов |
| 1 inch (дюйм) | 12 линий=25,4 мм=2,54 см |
| 1 line (линия) | 2,1 мм =6 точек =0,21 см |
| 1 point (точка) | 0,3528 мм=1/72 дюйма=0,0352 см |
Содержание отчета:
1. Название работы;
3. Выполненное задание
4. Отчёт составить по форме:
| Задание | Ответ |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. |
5.Ответы на контрольные вопросы.
Контрольные вопросы:
1. Назовите основные и дополнительные единицы системы СИ?
2. Как образуются кратные и дольные единицы Международной системы единиц?
3. Что называют единицей физической величины?
4. Принципы образования производных единиц Международной системы?
5. Что такое физическая величина?
6. Что такое размер физической величины?
7. Что такое системные, внесистемные единицы?
8. Для каких целей создавалась метрическая система мер?
Практическая работа № 2
Погрешности.
Цель работы:
1. Изучение видов измерений и погрешностей.
2. Научиться определять погрешности при прямых и косвенных измерениях
Задание: Определить:
1. Величину сопротивления и мощность по показаниям прибора, Таблица 2.
2. Максимальные абсолютные погрешности амперметра и вольтметра, формулы 6 и 7.
3. Абсолютную погрешность косвенного метода, Таблица 2.
4. Относительную погрешность измерения, Таблица 2.
5. Пределы действительных значений измеряемых физических величин.
| Наименование заданной величины | Вариант | ||||||
| Предел измерения Umax, В | |||||||
| Класс точности γU, % | 1.5 | 1.5 | 1.5 | 2.5 | 2.5 | ||
| Предел измерения Imax, А | |||||||
| Класс точности γI, % | 1.5 | 1.5 | 1.5 | 2.5 | 1.5 | 1.5 | 1.5 |
| Показаниявольтметра Uизм, В | |||||||
| Показанияамперметра Iизм, А | 1,3 | 5,2 | 6,7 | ||||
| Наименование заданной величины | Вариант | ||||||
| Показания вольтметра Uизм, В | |||||||
| Показания амперметра Iизм, А | 4,8 | 2,6 | 4,8 | 6,7 | 21,6 | ||
| Наименование заданной величины | Вариант | ||||||
| Показания вольтметра Uизм, В | |||||||
| Показания амперметра Iизм, А | 5,2 | 6,8 | 0,5 | 0,55 | 1,28 | 5,5 | 20,7 |
Оборудование, наглядные пособия: калькулятор
Теоретические основы:
Все производимые измерения можно классифицировать:
– по способу получения числового значения измеряемой величины;
– по видам измерений;
– по характеру изменения измеряемой величины в ходе измерения;
– по количеству измерительной информации;
– по отношению к основным единицам.
По способу получения числового значения измеряемой величины измерения могут быть прямые, косвенные, совокупные и совместные.
При прямых измерениях измеряемую величину сравнивают с ее мерой. Например, измерения длины линейкой с делениями, электрического тока амперметром и т.д.
Различают несколько методов прямых измерений.
Метод непосредственной оценки заключается в том, что значение величины определяют непосредственно по отсчетному устройству измерительного прибора прямого действия. К таким приборам относятся: вольтметры, амперметры, расходомеры, часы, манометры и т.п.
Метод сравнения с мерой состоит в том, что измеряемую величину сравнивают с величиной, воспроизводимой мерой. При этом методе измеряемую величину определяют путем непосредственного сравнения с мерой данной величины, например, измерение массы на рычажных весах с уравновешиванием гирями.
Метод противопоставления заключается в том, что измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения, с помощью которого устанавливается соотношение между этими величинами, например, измерение массы на равноплечих двухчашечных весах с помощью уравновешивающих гирь.
Дифференциальный метод заключается в том, что на измерительный прибор воздействует разность измеряемой величины и известной величины, воспроизводимой мерой, например, измерения, выполняемые при поверке мер длины сравнением с образцовой мерой на компараторе.
Компаратор — прибор, с помощью которого сравниваются поверяемое и эталонное средства измерений.
Нулевой метод заключается в том, что результирующий эффект воздействия измеряемой величины и меры на прибор для сравнения доводят до нуля, например, измерение электрического сопротивления мостом с полным его уравновешиванием.
Метод совпадений состоит в том, что разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадения отметок шкал или периодических сигналов, например, измерение длины штангенциркулем: наблюдают совпадение отметок на шкалах штангенциркуля и нониуса.
При косвенных измерениях измеряется не сама измеряемая величина, а другие величины, которые связаны с искомой определенной зависимостью. Например, среднюю скорость поезда на перегоне можно определить, зная длину перегона и время движения поезда по этому перегону. Пример косвенного измерения
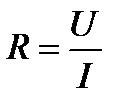
в которое подставляют результат прямых измерений падения напряжения U и протекающего через резистор тока I.
— мощности P = U∙I Вт.
При косвенных измерениях искомое значение величины у определяется на основании математической зависимости, связывающей эту величину с несколькими величинами, измеряемыми прямыми методами. При этом погрешности прямых измерений приводят к тому, что окончательный результат имеет погрешность.
Совокупные измерения сопряжены с решением системы уравнений, которые составляют по результатам одновременных измерений нескольких однородных величин. Например, в сложной электрической цепи, представляющей собой несколько ветвей с известными электрическими сопротивлениями и источниками нескольких ЭДС, необходимо вычислить величину токов в каждой ветви, предварительно измерив величину ЭДС. Применяя законы Кирхгофа или методы контурных токов, составляют систему уравнений и вычисляют величину токов в каждой ветви.
Совместные измерения — это измерения двух и более неоднородных физических величин для определения зависимости между ними. В качестве примера совместных измерений можно привести нахождение функциональной зависимости между длиной металлического стержня и температурой окружающей среды; частоты вращения вала электродвигателя постоянного тока в зависимости от приложенного момента к этому валу.
Измерения бывают следующих видов: электрические, магнитные, радиотехнические, теплотехнические, линейные, угловые, пространственные, измерения массы, объема, плотности, силы, скорости, ускорения, времени, оптические, ионизирующих излучений, определение состава и физико-механических свойств материалов.
По характеру изменения измеряемой величины измерения бывают статические и динамические.
Статические измерения — это измерения постоянных величин, например, измерение площади земельного участка.
Динамические измерения связаны с такими величинами, которые изменяются в процессе измерения, например, измерение количества электроэнергии электросчетчиком.
По количеству измерительной информации измерения бывают однократные и многократные.
При однократных измерениях число измерений равно числу измеряемых величин. Однако это сопряжено с невысокой точностью измерений. Поэтому чаще всего производят трехкратное измерение одной и той же величины и находят конечный результат как среднее арифметическое значение.
При многократных измерениях число измерений равно числу измеряемых величин. В научных исследованиях одну и ту же величину измеряют около 30 раз.
По отношению к основным единицам измерения подразделяются на абсолютные и относительные.
При абсолютных измерениях производят прямое измерение одной (иногда нескольких) основной величины и используют физическую константу. Например, в формуле определения высоты: H = gt 2 /2 измеряют время (t), а ускорение свободного падения (g) — физическая константа.
При относительных измерениях определяют отношение измеряемой величины к однородной, применяемой в качестве единицы. Например, относительная влажность определяется как отношение упругости водяного пара, содержащегося в воздухе, к упругости насыщенного пара при той же температуре и выражается в процентах. Построение характеристик в относительных единицах широко применяют в электроприводе, электрических машинах и т.д.
Любой результат измерения содержит погрешность.
Погрешность измерений — это отклонение значений величины, найденной путем ее измерения, от истинного (действительного) значения отклоняемой величины.
Погрешность прибора — это разность между показанием прибора и истинным (действительным) значением измеряемой величины. При анализе измерений сравнивают истинные значения физических величин с результатами измерений. Отклонение результатов измерений (Х) от истинного значения измеряемой величины (Х ист) называют погрешностью измерений (ΔХ).
Это теоретическое определение, так как истинное значение величины неизвестно. При метрологических работах вместо истинного значения используют действительное Хдейст, соответствующее показаниям эталонов.
По форме числового выражения погрешности измерений подразделяются на абсолютные и относительные.
Абсолютной называют погрешность измерения, выраженную в тех же единицах, что и измеряемая величина. Например, 0,25 В; 0,006 мм и т.д. Абслютная погрешность определяется по формулам (1) и (2). Практического применения абсолютные погрешности не имеют. Например, по образцовому вольтметру сравнивали показания двух рабочих вольтметров. Измеряли напряжение 10 В и получили погрешность 0,4 В, а другим — измеряли напряжение 1000 В и получили погрешность 10 В. На первый взгляд более точным кажется первый вольтметр, так как у него меньшая погрешность. Однако достоверную оценку приборов можно получить, используя относительную погрешность δ, которая равна отношению абсолютной погрешности к действительному значению измеряемой:
Определим относительную погрешность вольтметров предыдущего примера: для первого вольтметра δ = (0,4/10)·100 % = 4 %, а для второго вольтметра δ = (10/1000)·100 % = 1 %. Как видно из примеров, меньшей относительной погрешностью обладает второй вольтметр.
Погрешности измерений обычно классифицируют по причинам их возникновения и по видам погрешностей.
В зависимости от причин возникновения выделяют следующие погрешности измерений:
Погрешность метода — это составляющая погрешности измерения, являющаяся следствием несовершенства метода измерений. Суммарная погрешность метода измерения определяется совокупностью погрешностей отдельных его составляющих (погрешности показаний прибора и блока концевых мер, погрешности, вызванные изменением температурных условий, и т.п.).
Погрешность отсчета — это составляющая погрешности измерения, являющаяся следствием недостаточно точного отсчета показаний средства измерений и зависящая от индивидуальных способностей наблюдателя. Погрешность отсчета можно разделить на две составляющие: погрешность интерполяции и погрешность от параллакса.
Погрешность интерполяции при отсчитывании происходит от недостаточно точной оценки на глаз доли шкалы, соответствующей положению указателя (например, стрелки прибора).
Погрешность от параллакса возникает вследствие визирования (наблюдения) стрелки, расположенной на некотором расстоянии от поверхности шкалы.
Случайные погрешности — составляющие погрешности измерения, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайными являются погрешности, возникающие вследствие нестабильности показаний измерительного прибора, колебаний температурного режима в процессе измерения и т.д. Эти погрешности нельзя установить заранее, но можно учесть в результате математической обработки данных многократных измерений, изменяющихся случайным образом при измерении одной и той же величины.
🎥 Видео
Механика Л13. 2022. Размерности физических величин. Пи теорема.Скачать

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ измерение 7 класс международная система единиц СИСкачать

7. Проблема размерности физических величин. Ацюковский В.А.Скачать

Физические величины. Измерение физических величин | Физика 7 класс #3 | ИнфоурокСкачать

Переводы в СИ за 10 минутСкачать

Урок 8 (осн). Преобразование единиц измерения физических величинСкачать

Определение расстояния по угловой величинеСкачать

Решение задач методом размерностиСкачать

Физические величины, единицы измерения и размерностиСкачать

Формула Муавра ➜ Вычислить ➜ (5+5i)⁷Скачать

Физика 7 класс (Урок№2 - Физические величины и их измерение. Измерение и точность измерения.)Скачать

Физические величины. Измерение физических величин. Система единицСкачать

Множество значений функции #14Скачать

О размерностях физических величин и их системностиСкачать

Величины. Размерность.Скачать

Урок 4 (осн). Измерение физических величин. Цена деления шкалы измерительного прибораСкачать

О размерностях физических величин и их системностиСкачать

Физика. 7 класс. Перевод единиц измеренияСкачать









