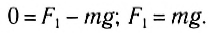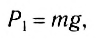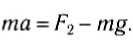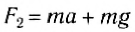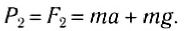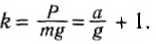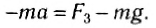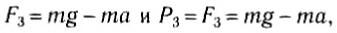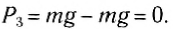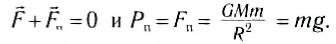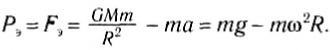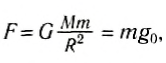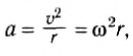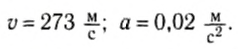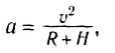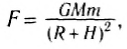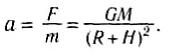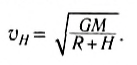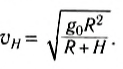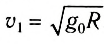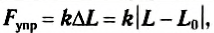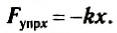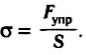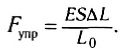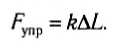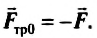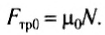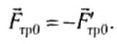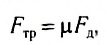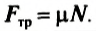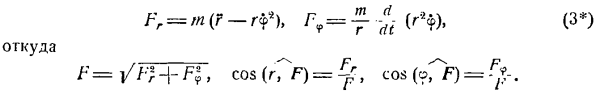
















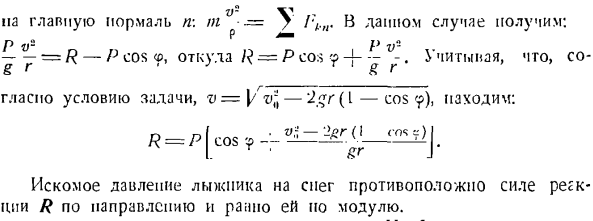
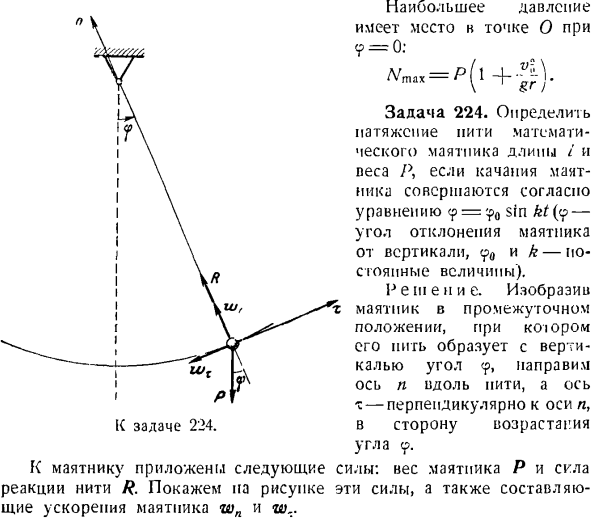


- Определение сил по заданному движению
- Определение сил по заданному движению
- Силы в механике — формулы и определение с примерами
- Сила тяжести
- Свободное падение тел (движение по прямолинейной траектории)
- Свободное падение тел (движение по криволинейной траектории)
- Вес тела
- Зависимость ускорения свободного падения от широты местности
- Сила упругости
- Закон Гука
- Механические свойства тел
- Силы сопротивления движению
- Силы трения скольжения и качения
- Вязкое трение
- 🎦 Видео
Видео:Наклонная плоскость. Расстановка сил | 50 уроков физики (6/50)Скачать

Определение сил по заданному движению
- Определение силы по конкретным движениям (Прямая задача динамики важных точек) Если уравнение импульса для точки массы mn задано в декартовых координатах: x -> ( / ), y = / a(/)、= = /、(/)、тогда проекции ΓX, yy и F, силы F-Fxi-j-FJ ^ — Fk для вызова этого движения определяются по формуле. Форекс = MXF и ФЗ = МЗ,(я ) Откуда? Ф = Я / интернет + ТФ-Н-Т、 потому что(ХГ>)=, потому что(г? Ф)= YG может, потому что(Z7 резца-Ф)=.
Поэтому прямая задача динамики важных точек может быть легко решена путем дифференцирования некоторого кинематического уравнения точек. Дано уравнение движения массы точки m вдоль траектории, то есть a = f (), проекции силы F = F Fn и Fh. R «r t-nn+, который вызывает это движение, определяется по формуле: Форекс = Ма£, рН = mvyt ФБ = 0, (2 ) Откуда? F = / F; — rn> cos (Γ>)= y, cos (Г>)=^, cos(0)= 0 В Формуле (2) vx =〜.
Сопротивление движению является функцией скорости лодки. Людмила Фирмаль
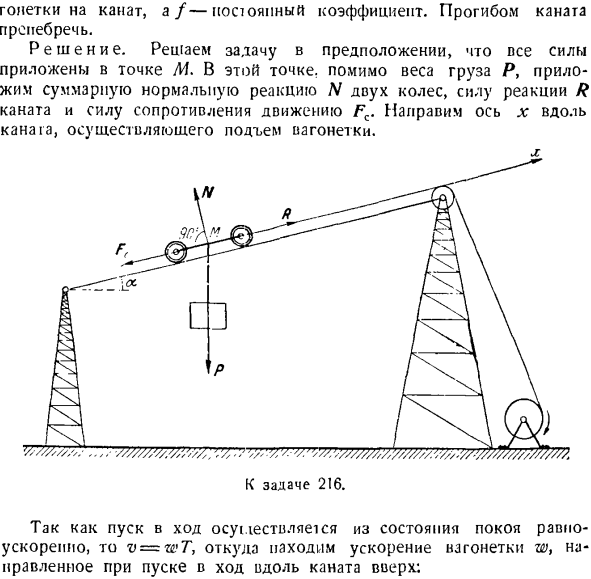
Учитывая уравнение планарного движения точки массы m в полярных координатах r = / 1 ( / ), синоу + ФК +£*. (Да б. Так… = / 7В = ФП потому что А, х = Ш = ^ Г、 Α= Р(синоу + / соз + ^ И я При равномерном движении тележки L * = 0, а Формула(1)принимает вид: Р = р(грех от J — / соз а). Требуемое натяжение каната равно модулю отталкивания R. задача 217.Масса Р определяет сопротивление воды движению лодки. П. С. x = — vQ(1-e p), где x> 0-средняя скорость движения, и- О Фиксированный коэффициент. Н. С. С. Цель 217.
Решение. Сила, приложенная к лодке: P-вес лодки, N-нормальная сила реакции воды, R-сила сопротивления воды движению лодки, а также направлена на противоположную сторону движения. проекция скорости лодки на ось Х — aJLt ЧХ = х * = vQe стр. (Т) Проекция ускорения лодки на ось x = = (2) напишите дифференциальное уравнение для движения лодки, спроецированной на ось X. Р М Л г. Используя формулу(2), можно увидеть следующее: [В] ГХ = — avttc». По условиям, сопротивление jR является функцией скорости лодки, поэтому при приведении Формулы (1) получаем Rx =-avx.
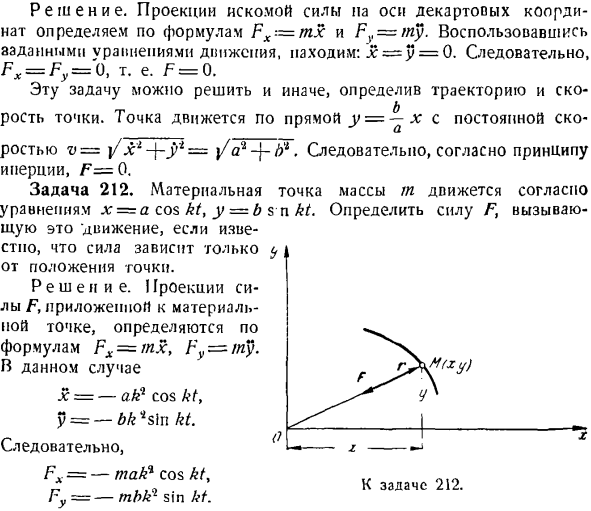
- Проблема 218.In в соответствии с Формулой x = a sin +Н грех о) Т—7 а -). (1) Потому что, согласно данному уравнению движения, как x = nut, n = — aui1 sin mt, т. е. х = — » л . (2) Подставляя значение l из Формулы (2) в Формулу (1), получаем: Γχ= — [pI sinЫ+ » Лг)). (3) Из уравнения движения заданной нагрузки sin= запишем Формулу (3) в виде: * ) На рисунке, в дальнейшем аналогичном случае, сила F направлена условно на R-уменьшенную сторону x-coordinate. In дело в том, что даже во время колебаний нагрузки сила F периодически меняется:
x = a, t. in в случае s при самом низком положении нагрузки сила упругости F достигает максимума 31 апексии. То есть, когда нагрузка проходит через положение статического равновесия. когда V = 0, сила упругости пружины равна весу груза. Задача 219.Автомобиль ve и P = 1200 кг движется по дну каньона с постоянным модулем скорости и= 36 км ’ НС. Определите давление автомобиля на дно оврага в наиболее интересующей точке. Радиус кривизны траектории p в этой точке равен 50 м, и мы будем рассматривать транспортное средство как точечную массу. Игнорируйте сопротивление движению.
Примените дифференциальное уравнение движения для массовой точки проекции к главной нормали Людмила Фирмаль
Решение: используйте естественную трехгранную ось, направив ось m горизонтально вправо, а ось n вертикально вверх. 2 силы приложены к автомобилю и приобретены как масса пункта. Масса P и нормальная реактивная сила R грунта, направленная вертикально вверх вдоль основной законной линии. //: С. С. В этом деле С. С. Откуда? 。 П. В.- С9. Если подставить число, то R = 1445 кг.
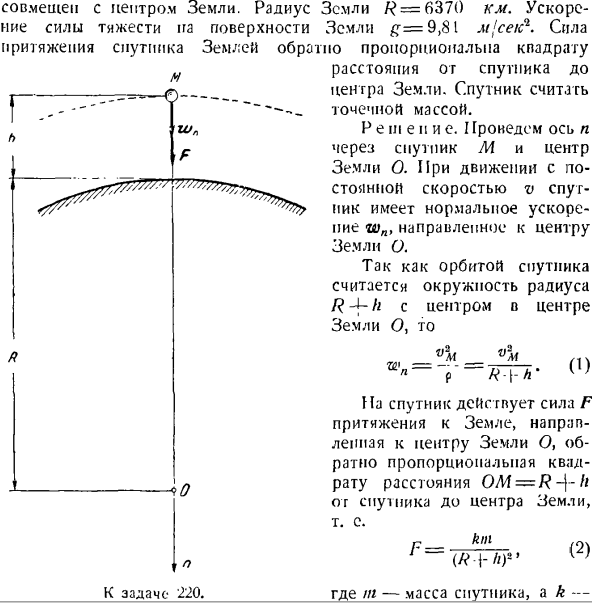
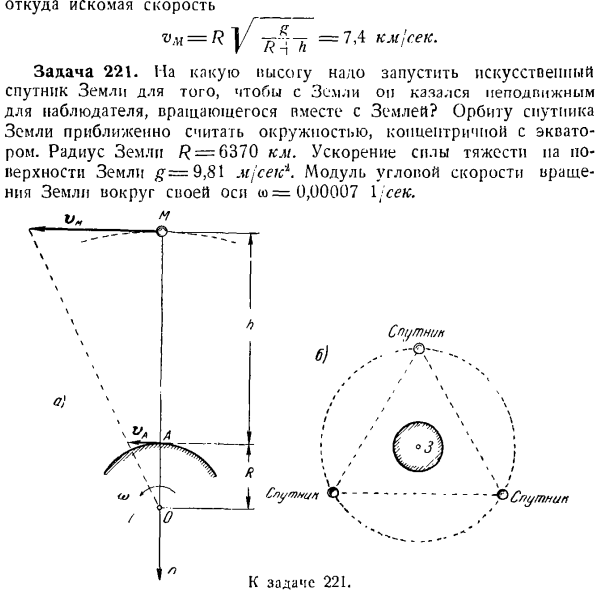
Требуемое давление транспортного средства на дне каньона направлено в противоположную сторону к нормальной силе реакции R, и величина ее равна. Проблема 220.Определите скорость, с которой спутник движется на высоте/ 2 = 900 км, если орбиту спутника можно сделать почти круговой в центре В сочетании с центром Земли. Радиус Земли а? = 6370 км. Гравитация земной поверхности гравитация£= 9.81 м сек спутника обратно пропорциональна квадрату Расстояние от спутника до центра Земли. Спутник считается точечной массой.
Решение. I ось Гройсмана n проходит через центр Земли O со спутником M. При движении с постоянной скоростью v спутник имеет нормальное ускорение wn, которое идет к центру Земли O. Так как орбита спутника представляет собой окружность радиуса R 4-h, центрированную по центру Земли O、 м. / — — — — — О —- То… ш= -^ — = «Го» Третий 0.) Я ’ Спутник находится под влиянием притяжения Земли к Земле, которое направлено в сторону центра Земли O, и обратно пропорционально расстоянию от спутника до центра Земли OM = R-]-H2. п = ._ км(2)
Да. н. К выпуску 220. ’(А * |-а) 2 «в» Где t-масса спутника, к- Ф — М(7-Ф£(Р!Φ), (3 *) Откуда? / ’ = / / .•; + ФДЖ, потому что(Р>)=^, потому что(φГ>)=^ -. Коэффициент пропорциональности. Что находится на поверхности Земли, то есть если h = 0, l:= P = mg, мы узнаем из уравнения (2): k = gR. Следовательно, гравитационное притяжение Далее пишем дифференциальное уравнение движения спутника и, как точку материи, проецируем его на ось N. мзн = Ф Используя Формулы(1)и(3), получаем следующее: , н я nifrR * И затем) IFL 4-NU vM = R j / » = 7,4 км лед k.
Где находится желаемая скорость Задача 221.At на какой высоте необходимо запустить искусственный спутник Земли, чтобы вращающийся наблюдатель с земли не казался сдвинутым с места искусственным спутником? Приблизительно предполагается, что орбита спутника Земли представляет собой окружность с экватором и концентрическую. Радиус Земли/? = 6370 км. Гравитационное ускорение земной поверхности # = 9.81 Мдж’Сик модуль угловой скорости вокруг земной оси равен= 0.00007 1 сек. Да.
Перейдите к выпуску 221. Спутник ^ Слу / ННК / ТКВ » б.) один.] 「* / / / У СГ / utnip да……. Гравитация спутника Земли обратно пропорциональна квадрату расстояния от спутника до центра Земли. Спутник считается точечной массой. The solution. To сделайте его похожим на искусственный спутник, который движется по экватору и концентрическим орбитам от Земли, пройдите через ось n, проходящую через спутник A, центр Земли O, и наблюдатель A на экваторе, и посмотрите на Землю (см. Рисунок A, схема Земли от Северного полюса).Согласно этому условию, скорости спутника M и наблюдателя
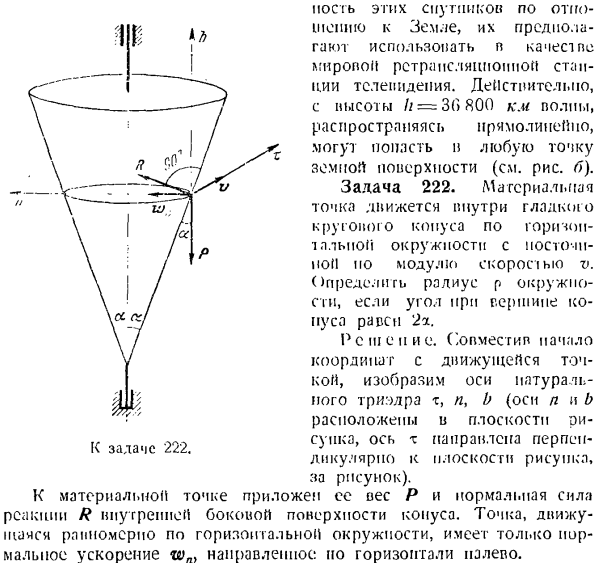
A должны удовлетворять следующему соотношению. _ Ом. ВА ОА ’ поскольку r> d = A> w, t0-отклонение угловой скорости вращения Земли за 1 день вокруг Земли: eV, R = R -/, OA = R, w v. w =(R•!- / / ) быть. Для предыдущего выражения задачи (-1) Это значение V. подставляя вместо ii, мы видим, что: (R-Λ)=^. г / м — / о -’ Где находится нужная высота * == Подставляя цифру, вы найдете нужную! Высота 36800 jc. tf. Существует проект по запуску 3 искусственных спутников на эту высоту, чтобы сформировать равносторонний треугольник, на вершине которого находятся спутники. Подумайте о том, чтобы не двигаться
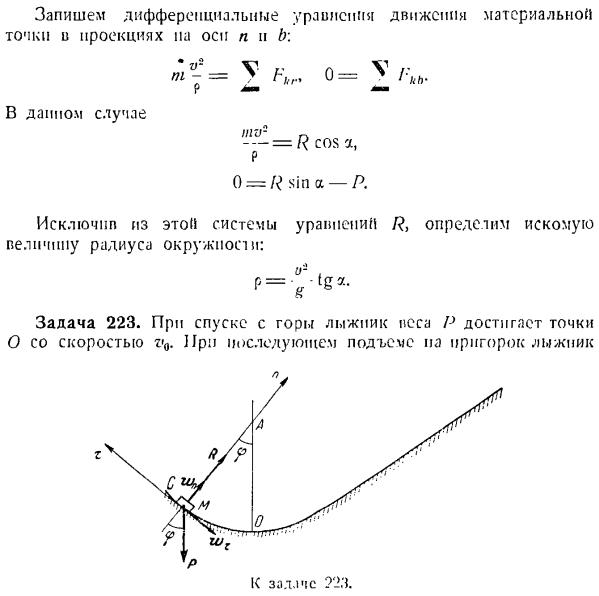
HOC l b этих спутников предполагается использовать в качестве всемирной телевизионной ретрансляционной станции по отношению к Earth. In дело в том, что с высоты// = 3 (>800 км) волны, распространяющиеся по прямой, могут достигать любой точки земной поверхности(см. Рисунок Б). Задача 222.Точка массы является пост-темпом, но движется в гладком конусе вдоль горизонтальной окружности по модулю скорости V. Если угол вершины конуса равен 2a, определите радиус окружности p. R и W E.
выравнивает начало координат до точки движения и изображает естественные трехгранные оси m, n и b (оси n и b «»’ находятся в плоскости 222 на supps ось x направлена на преступника. Особенно на плоскости изображения, для каждого изображения). Вес P и нормальная сила реакции R на внутренней поверхности конуса приложены к точке массы. Только нормальное ускорение wn>направлено к точке, которая равномерно движется по горизонтальной окружности.
Горизонталь-это олененок. Напишите дифференциальное уравнение движения точки масс в проекции осей n и b. = В 0 = УКБ. В этом деле ИГ — — — = Р потому что, п О = Р грех-Р Исключение R>из этой системы уравнений определяет искомое значение радиуса окружности. Р = vtga- Задача 223.При спуске с горы лыжник с весом P достигает точки O на скорости v0.Затем, когда вы поднимаетесь на холм, лыжник Проблема 72’x. Вдоль дуги окружности OS радиуса r скорость v = Y vij — ’2gt•((где’ f-cos-угол, образованный вертикальной линией и радиусом AM. Считается как точечная масса. Решение.
Траектория катания известна. Изобразим естественное трехгранное естественное по, определив его происхождение в точке А/, занятой текущим лыжником. К лыжнику были приложены следующие усилия. P-лыжная собака, обычная сила реакции снега, которая идет от M к центру L по радиусу дуги R-OS. Представляет нормальную wn и касательную w. компоненты ускорения лыжника. Примените дифференциальное уравнение движения к проекции для определения нормальной силы реакции R В. В.•
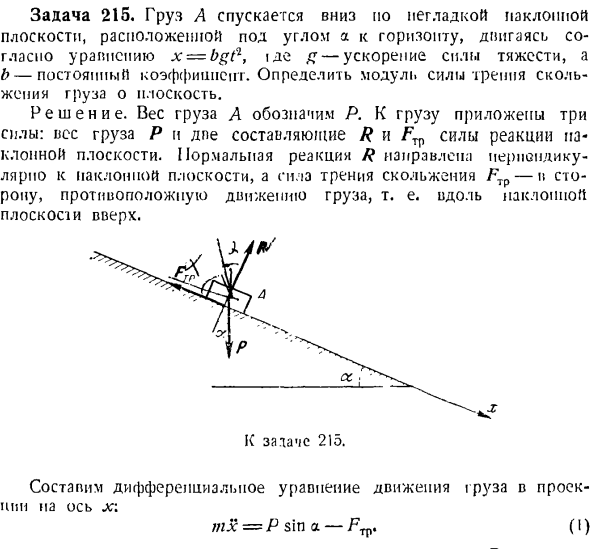
Основной нормальный n t■ -=?В этом случае P v-P v- — г = р-в ^ ОС .Необходимое натяжение кабеля равно коэффициенту реактивной силы R. Проблема 215.Груз а спускается по гладкой наклонной плоскости, двигаясь по формуле х-БГП, под углом а относительно горизонтальной плоскости.> > де g-ускорение свободного падения, А B-постоянный коэффициент. Определите коэффициент силы трения скользящей нагрузки на плоскость.
Решение. Вес груза A выражается в R. 3 силы прилагаются к грузу. Вес груза P и сила реакции наклонной плоскости составляют 2 составляющие, R и FTr. Нормальная сила реакции R направлена перпендикулярно наклонной плоскости, сила трения скольжения FT?- По направлению, противоположному движению груза, то есть по склону создайте дифференциальное уравнение для движения груза, спроецированного на ось X. = Р ЗША — / в(я)




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:13.1. Определение сил по заданному движениюСкачать

Определение сил по заданному движению
ДИНАМИКА ТОЧКИ
Определение сил по заданному движению
13.1.1Точка массой m=4 кгдвижется по горизонтальной прямой с ускорениемa=0,3t. Определить модуль силы, действующей на точку в направлении ее движения в момент времени t=3c. (3.6) Решение:Зная массу и ее ускорение, можно определить действующую на точку силу, в момент времени t=3c , ускорение будет  тогда тогда  |
13.1.2Ускорение движения точки массой m=27кгпо прямой задано графиком функции a=а(t). Определить модуль равнодействующей сил, приложенных к точке в момент времени t=5c. (4,05) Решение:Из графика видно что при t=5c , ускорение а=0,15м/с 2 , тогда 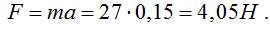 |
13.1.3 Деталь массой m=0,5кг скользит вниз по лотку. Под каким углом к горизонтальной плоскости должен располагаться лоток, для того чтобы деталь двигалась с ускорением а=2 м/с 2 ? Угол выразить в градусах. (11,8) Решение:Деталь движется под силой тяжести G=mg, сила под которой она движется по  лотку с некоторым углом а, лотку с некоторым углом а,  |
13.1.4Точка массой m=14кгдвижется по горизонтальной оси Ох с ускорениемах.=lnt Определить модуль силы, действующей на точку в направлении движения в момент времени t=5c. (22,5) Решение:  |
13.1.5Трактор, двигаясь с ускорением а=1м/с 2 по горизонтальному участку пути, перемещает нагруженные сани массой 600кг. Определить силу тяги на крюке, если коэффициент трения скольжения саней f=0,04. (835) Решение:Необходимая сила тяги на крюке для перемещения саней с заданным ускорением 1м/с 2 :  |
13.1.6Тело массой m=50 кг, подвешенное на тросе, поднимается вертикально с ускорением а=0,5м/с 2 . Определить силу натяжения троса.(516) Решение:  |
13.1.7 Скорость движения точки m=24кг по прямой задана графиком функцииv=v(t). Определить модуль равнодействующей сил, действующих на точку. (36) Решение: из графика функции v=v(t) видно, что точка движется равноускоренно с ускорением а=1,5м/с, тогда равнодействующая сил  |
13.1.8 Материальная точка массой m=12кгдвижется по прямой со скоростьюv=е 0,1t . Определить модуль равнодействующей сил, действующих на точку в момент времени t=50c.(178) Решение:  |
13.1.9 Определить модуль равнодействующей сил, действующих на материльную точку массой m=3кг в момент времени t=6c, если она движется по оси Ох согласно уравнению х=0,04t 3 . (4,32) Решение:Ускорение точки найдем из уравнения движения (вторая производная по времени): 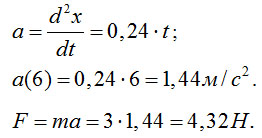 |
13.1.10 Материальная точка массой 1,4кг движется прямолинейно по законух=6t 2 +6t+3 . Определить модуль равнодействующей сил, приложенных к точке.(16,8) Решение:  |
Определение сил по заданному движению
Видео:Урок 87. Движение по наклонной плоскости (ч.1)Скачать

Силы в механике — формулы и определение с примерами
Содержание:
Закон всемирного тяготения:
Каждый из нас на личном опыте ощущает силу притяжения к Земле, благодаря которой мы можем ходить и бегать. Но, споткнувшись, именно под действием этой силы мы падаем на землю. В 7-м классе вы узнали, что эта сила называется силой тяжести и определяется произведением массы тела на ускорение свободного падения:
Почему Земля притягивает все тела? Чем определяется модуль ускорения падающего на Землю тела и, следовательно, сила притяжения к Земле?
Какие причины вызывают движение Луны вокруг Земли практически по круговой орбите?
Почему планеты Солнечной системы и в том числе наша Земля движутся вокруг Солнца?
Ньютон был первым ученым, который сначала высказал гипотезу, объясняющую все эти явления, а потом строго ее доказал. Он предположил, что между любыми телами существуют силы тяготения, и, например, падение камня и движение Луны по своей орбите определяется силой притяжения Земли. Чтобы установить закон, которому подчиняются силы тяготения, Ньютон сравни траектории и ускорения этих тел.
Камень, брошенный горизонтально с некоторой начальной скоростью, двинется к Земле по криволинейной траектории (рис. 54). Если увеличивать начальную скорость бросания, то дальность полета тела также возрастает. Из-за кривизны поверхности Земли при определенной начальной скорости камень вообще может не достигнуть Земли и начнет двигаться вокруг нее подобно Луне (рис. 55).

Рис. 55
Из этого мысленного эксперимента Ньютон сделал вывод, что движение камня и движение Луны обусловлены одной и той же причиной — притяжением Земли.
В то же время, по известным астрономическим данным (расстоянию до Луны и периоду ее обращения вокруг Земли), можно было определить ускорение Луны. Вычисленное таким образом центростремительное ускорение Луны оказалось равным 0,0027 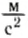
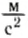
Так как Луна приблизительно в 60 раз дальше от центра Земли, чем камень, то Ньютон предположил, что ускорение, которое сообщает телам сила тяготения Земли, обратно пропорционально квадрату расстояния до центра Земли. Поскольку ускорение прямо пропорционально действующей на тело силе, то сила тяготения Земли также по величине обратно пропорциональна квадрату расстояния до центра Земли.
Зависит ли сила тяготения от массы тел? Опыты Галилея доказали, что ускорение свободного падения не зависит от массы тела. Это возможно только в том случае, если сила тяготения пропорциональна массе тела: F
m. Действительно, тогда увеличение или уменьшение массы, например, в два раза вызовет соответствующее изменение силы тяготения в два раза, но ускорение по второму закону Ньютона останется прежним:
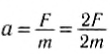
C другой стороны, во взаимодействии всегда участвуют два тела, на каждое из которых по третьему закону Ньютона действуют одинаковые по модулю силы. Следовательно, сила тяготения должна быть пропорциональна массе обоих тел. Так Ньютон пришел к выводу, что сила тяготения между телом и Землей прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между их центрами:
Выполняется этот закон только для Земли или является всеобщим?
Чтобы ответить на этот вопрос, Ньютон рассмотрел кинематические законы движения планет Солнечной системы, сформулированные немецким ученым Иоганном Кеплером на основании многолетних астрономических наблюдений датского ученого Тихо Браге.
Орбиты, по которым движутся планеты под действием силы тяготения Солнца, очень близки к круговым. Тогда один из законов Кеплера может быть записан в форме:
где T1 и T2, R1 и R2 — периоды обращения и средние радиусы орбит при вращении вокруг Солнца двух каких-либо планет Солнечной системы.
Используя формулу 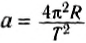
Ньютон доказал, что силы тяготения между планетами и Солнцем также подчиняются установленной им закономерности, и в 1667 г. сформулировал закон всемирного тяготения.
Так как размеры планет много меньше их расстояний до Солнца, то планеты можно рассматривать как материальные точки. В этом случае формулировка закона всемирного тяготения наиболее точна:
две материальные точки притягиваются друг к другу с силами, модули которых прямо пропорциональны произведению масс этих точек и обратно пропорциональны квадрату расстояния между ними (рис. 56, а):
Если размерами взаимодействующих тел нельзя пренебречь, то, чтобы определить силу тяготения между ними, необходимо разбить тела на такие малые обьемы, которые можно было бы считать материальными точками. Для нахождения силы тяготения между телами необходимо будет найти все силы притяжения между этими «материальными точками» и векторно их сложить.
Если тела представляют собой однородные шары массами m1 и m2, то расчеты показывают, что формула для силы тяготения между ними будет такая же, как и для материальных точек, но в этом случае r — расстояние межlу центрами шаров (рис. 56. 6).
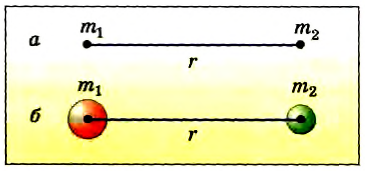
Рис. 56
Коэффициент пропорциональности G называется гравитационной постоянной (лат. gravitas — тяжесть). Определить величину гравитационной постоянной на основании астрономических данных Ньютон не мог, так как массы планет и Солнца в то время были не известны.
Впервые эта величина была определена в 1798 г. английским физиком Кавендишем с помощью прибора, называемого крутильными весами (рис. 57). Основной частью этого прибора было легкое коромысло с двумя шарами на концах, подвешенное на упругой проволоке. Рядом с ними неподвижно закрепляли два тяжелых шара. Под действием сил тяготения между этими шарами и подвешенными шарами коромысло поворачивалось на некоторый угол.
Зная величину этого угла, массы взаимодействующих тел, расстояния между их центрами и упругие свойства проволоки, Кавендиш рассчитал величину гравитационной постоянной:
Н* м2
Современное значение гравитационной постоянной 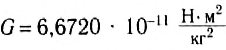
Силы всемирного тяготения самые универсальные из сил природы, так как действуют между любыми телами. Но из-за такой малой величины гравитационной постоянной силы тяготения являются значительными только для тел с очень большой массой, например для планет и других космических тел.
Если известен кинематический закон движения спутника какого-либо космического тела (планеты, звезды, кометы), то, используя закон всемирного тяготения и второй закон Ньютона, можно рассчитать массу этого тела. Так и были определены массы различных космических тел (рис. 58): Солнца, Луны, Земли, других планет и их спутников.
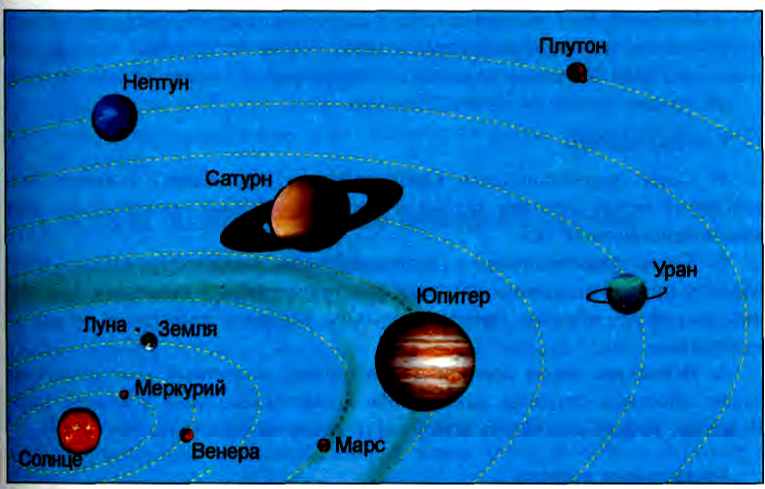
Рис. 58
При изучении физики в 8-м и 9-м классах вы узнали, что электрические и магнитные взаимодействия тел определяются существующими вокруг них электрическими и магнитными полями.
Аналогично вокруг любого тела существует особая форма материи — гравитационное поле, характеристики которого зависят от массы тела. Если масса одного тела много больше массы другого, то его гравитационным полем можно пренебречь по сравнению с полем первого тела. Поэтому говорят, например, что самолет движется в гравитационном поле Земли или планеты Солнечной системы движутся в гравитационном поле Солнца.
Закон всемирного тяготения стал важнейшей ступенью в развитии всей физики, так как выявил новое свойство массы тела.
Сила гравитационного взаимодействия пропорциональна массам тел, т. е. масса является мерой тяготения, и, следовательно, ее можно назвать гравитационной.
Во втором законе Ньютона масса определяет инертные свойства тела, т. е. его способность приобретать большее или меньшее ускорение, и ее естественно назвать инертной.
Одинаковы ли эти массы? Многочисленные опыты показывают, что эти массы равны друг другу.
Опытный факт равенства гравитационной и инертной масс, называемый принципом эквивалентности, Альберт Эйнштейн положил в основу общей теории относительности, обобщающей и уточняющей более простую теорию тяготения Исаака Ньютона.
Главные выводы
- Силы гравитационного взаимодействия (тяготения) универсальны, действуют между любыми телами и пропорциональны произведению масс взаимодействующих тел.
- Силы гравитационного взаимодействия двух материальных точек обратно пропорциональны квадрату расстояния между ними, для однородных шаров — обратно пропорциональны квадрату расстояния между их центрами.
- Используя закон всемирного тяготения, известный кинематический закон движения спутника какого-либо космического тела и второй закон Ньютона, можно рассчитать массу этого космического тела.
Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Сила тяжести
Как мы уже обсуждали, исторически сложилось, что силой тяжести 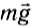
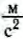
Измерения, проведенные в различных точках поверхности Земли, показывают, что ускорение свободного падения может иметь различные значения, а 9,8 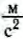
Теперь вы знаете, что силу, с которой на тело действует Земля, можно рассчитать по закону всемирного тяготения. Будем считать Землю однородным шаром массой M и радиусом R. Любое тело по сравнению с нашей планетой можно считать материальной точкой. Если тело находится на небольшой высоте h≪R от поверхности Земли (или h = 0), то можно записать для силы их гравитационного взаимодействия:
Сравнивая модули силы тяжести и гравитационного взаимодействия, можно найти модуль ускорения свободного падения:
Полученная формула показывает, что ускорение свободного падения зависит только от массы Земли и ее радиуса, и поэтому его модуль одинаков для всех тел.
Если высотой тела над поверхностью Земли нельзя пренебречь, то расстояние между телом и центром земного шара равно r = R + h, и модуль ускорения свободного падения будет тем меньше, чем дальше тело от поверхности.
Поэтому часто для ускорения свободного паления вблизи поверхности вводят индекс «0», а для ускорения свободного падения на некоторой высоте от поверхности Земли — индекс «h»:
Следовательно, и модуль силы тяжести будет отличаться при различном расположении тела относительно поверхности Земли: mg0 или mgh.
Какую удивительную возможность дает нам полученная формула для g0?
Эта формула позволяет определить массу нашей планеты (рис. 59), ведь среднее значение модуля ускорения свободного падения и средний радиус Земли уже давно определены опытным путем:
Именно потому, что с помощью закона всемирного тяготения возможны подобные расчеты, его иногда в шутку называют «всемирными весами».
Аналогично можно получить формулы для ускорения свободного падения и силы тяжести вблизи любого космического тела: Луны, Марса, Солнца, только в них соответственно будут входить масса и радиус этого космического тела.
Так как мы получили формулы для ускорения свободного падения, рассматривая самую простую модель гравитационного взаимодействия, то иногда говорят, что это формулы для расчета ускорения свободного падения в «первом приближении».
Какие еще факторы влияют на модуль ускорения свободного падения, например, вблизи данной точки земной поверхности?
- Земля не является шаром. Форма нашей планеты в честь ее греческого имени Гея носит название «геоид», так как радиус кривизны ее поверхности у полюсов больше, чем на экваторе.
- Наша планета не однородна по строению, состоит из различных слоев, в которых есть области различной плотности, например залежи нефти и газа или залежи тяжелых металлов.
- В рассмотренной модели не учтено суточное вращение Земли.
- При расчетах не учитывалось гравитационное взаимодействие тела с другими космическими телами: Луной, Солнцем и т. п.
Именно поэтому модуль ускорения свободного падения отличается для различных точек на поверхности Земли. Например, на полюсах 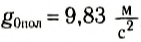
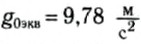
При решении задач, если в условии ничего не сказано о форме планеты, ее строении, параметрах вращательного движения, используется рассмотренная нами простейшая модель гравитационного взаимодействия и полученные формулы.
Главные выводы:
- Причиной существования силы тяжести является гравитационное взаимодействие между телом и Землей.
- Если не учитывать особенности строения и формы Земли и участие ее во вращательном движении, то модуль ускорения свободного падения определяется только ее массой и радиусом.
- При удалении от поверхности Земли модули ускорения свободного падения и силы тяжести уменьшаются.
Видео:Расчёт массы и объёма тела по его плотности. Физика 7 классСкачать

Свободное падение тел (движение по прямолинейной траектории)
Каждый человек в своей жизни наблюдал движение различных тел под действием силы притяжения к Земле (рис. 60). Падает вниз с парты ручка или резинка, плавно опускается лист дерева, движется по сложной траектории после удара мяч и т. п. Причем каждый наблюдал, что если с одной ветки одновременно начали падать лист и яблоко, то яблоко движется быстрее.

Рис. 60
На основании таких наблюдений до опытов известного итальянского ученого Галилео Галилея считалось, что более тяжелые тела с одной и той же высоты падают быстрее, чем легкие. По преданию, Галилей изучал падение различных тел со знаменитой Пизанской башни (рис. 61) и установил, что все тела, независимо от их массы, падают с одинаковым ускорением, если их движению ничто не мешает.

Рис. 61
Проведем такой опыт. В стеклянную трубку, один конец которой запаян, а другой закрыт пробкой с краном, поместим птичье перо, кусок пенопласта и свинцовую дробинку. Перевернув трубку, мы обнаружим, что эти тела упадут на дно не одновременно (рис. 62, а): первой на дне окажется свинцовая дробинка, а позже всех упадет птичье перо. Так, может, не прав Галилей?
Чтобы ответить на этот вопрос, проведем опыт при других условиях. Откачаем насосом воздух из трубки, закроем кран и вновь быстро перевернем трубку. Теперь все три предмета упадут на дно трубки одновременно (рис. 62, б), потому что их движению не мешает воздух, и, следовательно, вывод Галилея подтверждается.
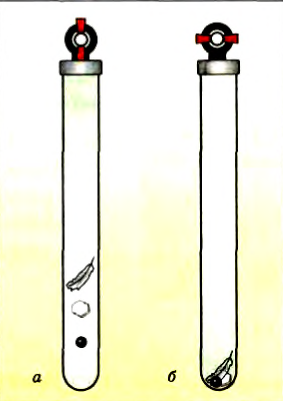
Рис. 62
Свободным падением называется движение тела только под действием силы тяжести с любой начальной скоростью.
Свободное падение — модель реального движения тела вблизи поверхности Земли под действием ее силы притяжения, при котором не учитываются суточное вращение Земли, размеры тела и сопротивление воздуха его движению. В физических задачах эта модель применяется при рассмотрении движения, например, падающего с горы камня, мяча после подачи игрока, пули, выпущенной из ружья, и т. п.
При этих условиях сила тяжести считается постоянной и рассчитывается по формуле 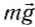
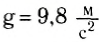
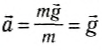
Поэтому разные тела движутся с одинаковыми ускорениями, как показано на рисунке 63. Этот рисунок сделан с фотографии, которую получили, открывая объектив и чередуя вспышки света каждые 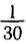

Рис. 63
Следовательно, свободное падение — частный случай равноускоренного движения, и если
Рассмотрим наиболее часто встречающиеся случаи свободного падения тела.
1) Пусть тело свободно падает без начальной скорости с высоты h над поверхностью Земли. Для описания механического движения необходимо выбрать систему отсчета, и в данном случае полезно рассмотреть движение тела в двух системах координат.
а) Выберем начало первой системы координат под точкой начала падения тела, а ось Oy направим вверх (рис. 64). Ось Ox не нужна, так как все векторы расположены вдоль оси Оу. Найдем проекции векторов и запишем уравнения для координаты и проекции мгновенной скорости:
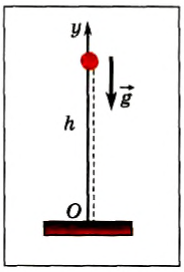
Рис. 64
Найдем время падения тела tk, используя то, что в последний момент движения тело попадает в начало выбранной оси Оу, т. е. его конечная координата равна:
Зная все время падения тела, можно найти проекцию его скорости в последний момент движения:
Проекция скорости тела отрицательна, так как скорость направлена противоположно выбранному направлению оси Оу.
б) Можно выбрать и другую систему координат (рис. 65). Тогда проекции векторов:
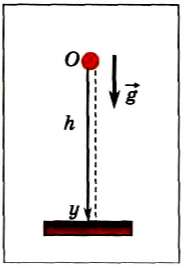
Рис. 65
и уравнения для координаты тела и для проекции мгновенной скорости в любой момент времени будут иметь вид:
В последний момент движения в этой системе отсчета конечная координата тела равна:
Отсюда все время движения:
а проекция конечной скорости тела:
Мы получили для расчета времени падения ту же формулу, а формула для проекции скорости отличается только знаком, указывающим направление скорости по отношению к выбранной системе координат.
Как и следовало ожидать, полученные результаты не зависят от выбора системы координат.
2) Рассмотрим другой случай свободного падения: тело брошено с начальной скоростью υ0, направленной вертикально вверх (рис. 66), и вернулось в точку бросания. Например, вы бросили вверх мяч и поймали его при возвращении.
Рис. 66
Выберем начало оси Oy в точке начала движения тела (рис. 67). Тогда проекции векторов:
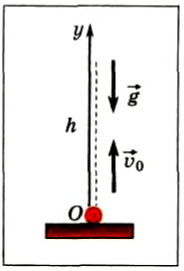
Рис. 67
Уравнения для координаты тела и для проекции мгновенной скорости в любой момент времени:
Найдем все время движения тела, или время возвращения тела в точку бросания tk, учитывая, что в последний момент движения тело попадает в начало оси Оу, т. е. его конечная координата:
Это квадратное уравнение имеет два корня:
которые соответствуют начальному моменту движения и моменту возвращения тела в исходную точку.
Найдем скорость тела в последний момент движения, подставив все время движения в уравнение для проекции скорости:
Отсюда следует: с какой скоростью мяч брошен вертикально вверх, с такой же скоростью по модулю, но противоположной по направлению, вернется в точку бросания (и ударит по бросившим его рукам!).
Найдем время подъема тела на максимальную высоту и значение этой высоты.
При движении тела вверх проекция мгновенной скорости уменьшается. В момент максимального подъема тело на мгновение останавливается (а затем начинает падать вниз), т. е. υty = 0 = υo-gtn. Тогда время подъема тела на максимальную высоту: 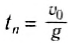
т. е. равно половине всего времени движения:
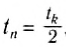
а максимальное значение координаты или высоты подъема:
или 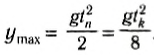
Следовательно, сколько времени тело поднималось до максимальной высоты, столько же времени с этой высоты возвращалось в исходную точку.
Можно показать, что для брошенного вертикально вверх тела: 1) скорость, с которой оно проходит при подъеме любую точку на некоторой высоте, равна по модулю и противоположна по направлению скорости, с которой оно проходит эту же точку на спуске; 2) время подъема тела между любыми двумя точками по вертикали равно времени падения между этими же точками.
Знание этих соотношений позволяет более просто решить некоторые задачи.
Если сопротивлением воздуха пренебречь нельзя, то время подъема вертикально брошенного тела до максимальной высоты всегда меньше времени возвращения с этой высоты, а конечная скорость при возвращении в исходную точку всегда меньше начальной.
Аналогично можно рассмотреть движение тела, брошенного вертикально вниз с некоторой высоты с начальной скоростью.
Главные выводы:
- Свободное падение — это движение тела только под действием силы тяжести.
- Если начальная скорость тела равна нулю или коллинеарна вектору ускорения свободного падения, то свободное падение представляет собой частный случай равноускоренного прямолинейного движения с ускорением:
.
- Для тела, брошенного вертикально вверх: а) скорость прохождения точки на некоторой высоте при подъеме равна по модулю и противоположна по направлению скорости при прохождении этой же точки на спуске; б) время подъема между двумя точками по вертикали равно времени падения между этими же точками.
Видео:Физика - уравнения равноускоренного движенияСкачать

Свободное падение тел (движение по криволинейной траектории)
Рассмотрим свободное падение тел в случаях, когда вектор начальной скорости направлен не вертикально. Для наглядного представления такой траектории удобно рассматривать полет струи воды, вытекающей под напором из шланга (рис. 68).

Рис. 68
Например, мяч в результате броска (рис. 69, а) начинает двигаться под углом к горизонту или во время игры человек бросает мяч в горизонтальном направлении (рис. 69,6). Из личного опыта каждый знает, что в обоих случаях мяч движется по криволинейной траектории. 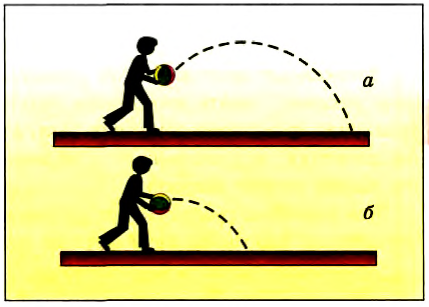
Рис. 69
1) При броске в горизонтальном направлении тело начинает движение со скоростью 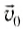
Выберем начало системы отсчета па вертикальной линии под точкой бросания (рис. 70). В этом случае векторы 
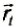
Тогда
и можно записать кинематические уравнения для координат тела и проекций его скорости:
Первые две формулы показывают, что координата х1 прямо пропорциональна времени, а проекция скорости на ось Ox не зависит от времени, т. е. эти уравнения соответствуют уравнению равномерного прямолинейного движения.
Две последние формулы описывают равноускоренное движение. Следовательно, рассматриваемое сложное движение в плоскости можно представлять в виде двух движений: одно — свободное падение без начальной скорости, а второе — равномерное движение в горизонтальном направлении.
Записанные кинематические уравнения позволяют решить основную задачу механики: найти координаты тела в любой момент времени, получить уравнение траектории движения тела, а также формулы для расчета времени движения, дальности полета, величины и направления скорости тела в последний момент движения.
Как известно, уравнение траектории представляет собой функциональную зависимость координат точки друг от друга. Получим уравнение траектории, х.
выражая время 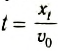
Следовательно, траектория движения тела представляет собой ветвь параболы.
Например, если при стрельбе по мишени спортсмен держит винтовку горизонтально, то пуля движется по параболе и за время полета до мишени опустится тем ниже начального уровня, чем дальше мишень. Это обязательно учитывают спортсмены, для того чтобы показать лучшие результаты.
Найдем полное время движения тела, используя то, что в выбранной системе отсчета конечная его координата равна нулю:
Полученная формула показывает, что полное время движения тела, начальная скорость которого направлена горизонтально, не зависит от ее значения. Следовательно, если два тела одновременно начали движение с одной и той же высоты, одно — горизонтально с начальной скоростью, а второе — вниз без начальной скорости, то они упадут одновременно (конечно, если не учитывать сопротивление воздуха).
Получим формулу для дальности полета тела, которую рассчитывают как расстояние, пройденное телом в горизонтальном направлении, т. е. в выбранной системе отсчета:
Из этой формулы следует, что, чем больше начальная скорость тела и высота, с которой оно брошено, тем больше дальность его полета.
Скорость тела направлена по касательной к параболической траектории (рис. 71), а ее модуль в любой момент времени можно найти по теореме Пифагора: 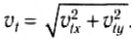
Угол между направлением скорости тела в любой момент движения и горизонталью можно определить из прямоугольного треугольника, образованного вектором скорости и его проекциями на оси координат (см. рис. 71):
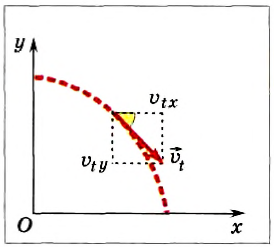
Рис. 71
Например, в последний момент движения:
Для описания движения тела, брошенного горизонтально, можно выбрать и другую систему отсчета. Попробуйте сделать это самостоятельно и описать движение тела в этой системе отсчета.
2) Движение тела, брошенного с начальной скоростью 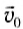
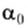
Пусть в конце движения тело возвращается на тот же уровень относительно Земли, с которого начало движение.
Выберем начало отсчета в точке бросания тела (рис. 72). Векторы 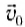
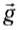
Тогда
и можно записать кинематические уравнения для координат точки и проекций ее скорости:
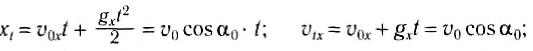
Из первых двух уравнений следует, что проекция скорости на ось Ox не зависит от времени, а координата x1 прямо пропорциональна времени, т. е. это кинематические уравнения равномерного движения.
Два последних выражения представляют собой кинематические уравнения равноускоренного движения.
Таким образом, сложное движение тела в плоскости можно представить как наложение двух простых, одномерных: равномерного вдоль оси Ox и равноускоренного вдоль оси Оу.
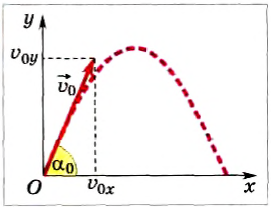
Рис. 72
Эти уравнения позволяют решить основную задачу механики: определить координаты тела в любой момент времени, а также рассчитать, например, время подъема на максимальную высоту и ее величину, все время движения и дальность полета тела, найти модуль скорости тела и ее направление в любой момент времени.
Получим уравнение траектории тела, выразив время из уравнения для координаты х1 и подставив в уравнение для координаты y1:
Так как 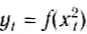
Найдем время подъема тела на максимальную высоту, используя уравнение для проекции скорости 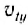
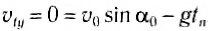
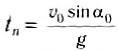
Найдем все время движения, используя уравнение для координаты y1, которая в выбранной системе отсчета в последний момент движения равна нулю:
Это квадратное уравнение имеет два корня, первый из которых соответствует начальному моменту времени t0 = 0, а второй — всему времени движения тела:
Следовательно, все время движения вдвое больше времени подъема, или сколько времени тело поднимается на максимальную высоту, столько же и спускается с нее.
Можно показать, что это же будет справедливо при полете тела по параболе между двумя любыми уровнями по высоте вверх и при полете по параболической траектории между этими же двумя уровнями вниз.
В выбранной системе отсчета дальность полета тела — его конечная координата по оси Ох:
Модуль скорости тела в любой момент времени можно найти по теореме Пифагора: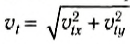
Например, в конечный момент времени:
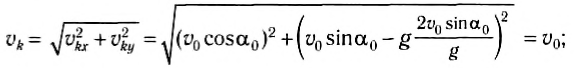
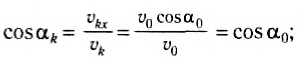
Эти выражения показывают, что конечная скорость тела равна по модулю начальной и направлена к горизонту под углом, равным по модулю первоначальному.
Можно показать, что при движении по параболической траектории модуль скорости и модуль угла, который вектор скорости образует с горизонтом. на любом одном и том же уровне относительно Земли одинаковы.
Используя понятия нормального и тангенциального ускорений, можно рассчитать радиус кривизны параболической траектории в любой момент времени. Как уже обсуждалось, вектор полного ускорения можно разложить на сумму тангенциального и нормального ускорений.
Разложим вектор ускорения свободного падения на векторы тангенциального и нормального ускорений (рис. 74): 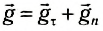
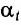
Так как 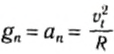
Если тело брошено под углом к горизонту с некоторой высоты над Землей, то необходимо вновь выбрать одну из систем отсчета и записать кинематические уравнения для координат и проекций скоростей, которые позволяют найти искомые величины.
Главные выводы:
- Если вектор начальной скорости тела лежит в вертикальной плоскости, но не коллинеарен вектору ускорения свободного падения, то тело движется по параболической траектории, расположенной в этой вертикальной плоскости.
- Сложное движение тела по параболической траектории можно представить в виде двух более простых движений: равноускоренного с
вдоль вертикального направления и равномерного вдоль горизонтального направления.
- Во многих случаях при описании движения тела по параболической траектории выбор оптимальной системы отсчета позволяет более рационально математически найти искомые физические величины.
Видео:Урок 106. Реактивное движениеСкачать

Вес тела
Силой веса 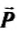
Под действием силы тяготения тело двигалось бы к Земле, но опора или подвес противодействуют силе притяжения. В результате этого в теле и опоре начинается процесс деформации, т. е. изменение формы и размеров. Этому процессу противодействуют силы взаимодействия между молекулами внутри вещества.
В механике для того, чтобы не рассматривать эти сложные межмолекулярные взаимодействия, вводят силу реакции опоры 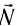
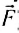
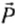
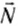
Следовательно, сила веса отличается от силы тяжести тем, что ее возникновение обусловлено силой тяготения и межмолекулярными силами в веществе, а сила тяжести — гравитационная сила. Кроме того, сила тяжести приложена к телу, а сила веса — к опоре или подвесу.
Рассмотрим, от чего зависит сила веса, ведь опора или подвес могут и покоиться относительно Земли, и двигаться с какой-либо скоростью или ускорением.
Пусть, например, тело массой m подвешено на динамометре, прикрепленном к потолку лифта (рис. 75). По второму закону Ньютона: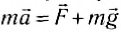
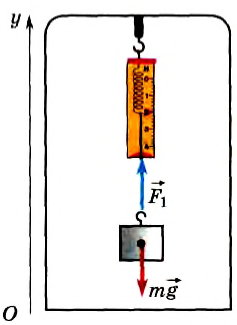
Рис. 75
Рассмотрим различные случаи движения лифта относительно инерциальной системы отсчета, связанной с Землей.
1) Пусть лифт покоится, и тогда ускорение лифта, подвеса и тела α = 0 (см. рис. 75). Спроецируем на ось Oy и выразим силу веса тела P1 в этом случае:
т. е. динамометр показывает вес, равный по модулю силе тяжести.
Если лифт поднимается вертикально вверх или спускается вертикально вниз равномерно, то ускорение его и тела также равно нулю, и мы получим тот же результат.
Следовательно, при равномерном вертикальном движении подвеса с телом или когда вся система покоится, сила веса равна силе тяжести, направлена в ту же сторону, но приложена к подвесу (или опоре).
2) Пусть лифт поднимается с постоянным ускорением, направленным противоположно вектору ускорения свободного падения: 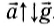
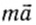
Для проекции на ось Оу:
Динамометр в этом случае показывает силу веса большую, чем сила тяжести тела, и чтобы характеризовать это явление, вводят термин перегрузка.
Чаще всего количественно перегрузку определяют как отношение силы веса к силе тяжести тела:
Перегрузки — одна из особенностей работы летчиков при выполнении фигур высшего пилотажа, космонавтов при старте космического корабля, гонщиков, участвующих в соревнованиях скоростных автомобилей. Тренированный человек может без серьезных последствий кратковременно выдержать примерно шестикратную перегрузку. Например, при взлете космического корабля стартовое ускорение не должно превышать 5g.
3) Пусть лифт движется с ускорением, направленным так же, как и ускорение свободного падения 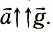
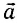
Для проекции на ось Оу.
т. е. в данном случае динамометр покажет вес меньше, чем сила тяжести тела. Но если ускорение по модулю a > 2g, то вес вновь будет больше силы тяжести.
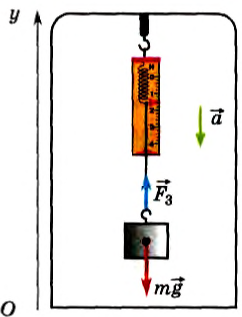
Рис. 77
Важно отметить, что при движении подвеса с ускорением, равным по модулю и направлению ускорению свободного падения 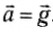
Чтобы охарактеризовать это явление, вводят понятие состояние невесомости, или невесомость, которое подразумевает отсутствие веса, так как тело с опорой или тело с подвесом движутся с ускорением свободного падения в пространстве вместе, но практически не взаимодействуют друг с другом (рис. 78).

Рис. 78
Так как тело не взаимодействует с опорой, то нет и деформации обоих тел.
Например, человек в условиях невесомости на космическом корабле испытывает особые ощущения, в его организме в определенной степени изменяются физиологические процессы. Это происходит потому, что человек на Земле всегда взаимодействует с какой-либо опорой, и, следовательно, все процессы в организме осуществляются при наличии деформации.
Например, деформация позвоночного столба при вертикальном положении человека приводит к тому, что в конце дня его рост меньше, чем утром.
Состояние невесомости при определенных условиях можно испытать в самолете. Если пренебречь сопротивлением воздуха, то можно считать, что на самолет, набравший скорость и движущийся с выключенными двигателями, действует только сила тяжести. При этих условиях для тел в самолете наблюдается состояние невесомости.
В некотором интервале можно подобрать такой угол между скоростью самолета и горизонтом в начальный момент движения, чтобы время безопасного полета с отключенными двигателями было достаточно для тренировки космонавтов или съемок эпизодов для кинофильмов.
Рассмотренные случаи отличия модуля веса от модуля силы тяжести возникают и при участии тела во вращательном движении. Например, вес тела, измеренный одним и тем же динамометром на полюсе Земли больше, чем вес этого тела на экваторе. Это связано с тем, что на экваторе тело вместе с динамометром и поверхностью Земли участвует во вращательном движении (рис. 79).
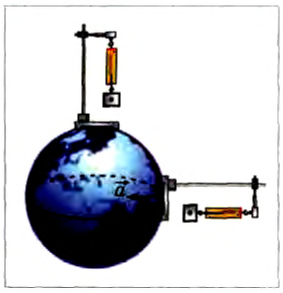
Рис. 79
Пусть 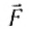
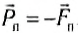
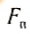
Следовательно, на полюсе вес тела равен по модулю силе тяжести.
На экваторе тело вместе с подвешенным к опоре динамометром движется с ускорением a = ω 2 R. где ω— угловая скорость вращения Земли, R — радиус Земли. Тело движется с этим ускорением под действием силы притяжения и силы со стороны динамометра: 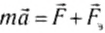
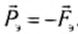
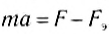
Из полученной формулы видно, что если бы угловая скорость вращения Земли вдруг начала возрастать, то при определенном ее значении вес тел на экваторе стал бы равным нулю.
Рассмотренные примеры иллюстрируют, что при решении различных задач вес тела должен определяться в каждом конкретном случае на основании второго и третьего законов Ньютона.
Главные выводы:
- Модуль веса тела в общем случае не равен модулю силы тяжести.
- Модуль веса тела зависит от характера движения тела и опоры (подвеса) и их взаимного расположения.
- При совместном движении тела и опоры или подвеса с ускорением свободного падения наблюдается состояние невесомости.
Видео:Все формулы молекулярной физики, МКТ 10 класс, + преобразования и шпаргалкиСкачать

Зависимость ускорения свободного падения от широты местности
До сих пор мы рассматривали простейшую модель, в которой приняли, что сила тяжести тела — это и есть сила его гравитационного взаимодействия с Землей. Но если сила тяжести совпадает с силой гравитационного тяготения, то она должна быть направлена вдоль радиуса Земли к ее центру.
На опыте направление силы тяжести можно определить по «отвесу» — направлению нити, на которой подвешен тяжелый груз. Например, каменщик, укладывая кирпичную стену, проверяет, вертикальна ли грань стены, именно таким способом (рис. 81).
Точные измерения показывают, что в каждой местности «отвесная линия» не совпадает с направлением на центр земного шара, т. е. направление силы тяжести не совпадает с направлением силы тяготения. Только на полюсах и экваторе земного шара сила тяжести направлена к его центру.
Как это можно объяснить? 
Рис. 81
Все точки поверхности Земли, за исключением полюсов, участвуют во вращательном движении вокруг земной оси.
Рассмотрим тело, лежащее в какой-то точке на поверхности Земли с широтой φ и участвующее вместе с ней в суточном вращении. Широтой данной точки местности, как известно, называется угол φ между радиусом Земли, проведенным в эту точку, и плоскостью экватора (рис. 82).
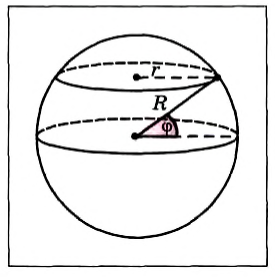
Рис. 82
Выберем начало инерциальной системы отсчета в центре земного шара, а оси координат направим на неподвижные звезды. Запишем закон всемирного тяготения, считая тело материальной точкой по сравнению с Землей:
где М — масса Земли, R — ее радиус, g0 — ускорение свободного падения на поверхности Земли без учета ее суточного вращения.
Тело движется по окружности радиуса r со скоростью 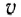
где ω — угловая скорость вращения Земли.
Для Беларуси, например, средние величины скорости вращения и центростремительного ускорения точек поверхности:
На покоящееся тело действуют сила тяготения со стороны Земли, направленная по радиусу к ее центру, и сила реакции опоры. По второму закону Ньютона: 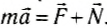
Рис. 83
В Солнечной системе вокруг многих планет вращаются космические тела, которые называют естественными спутниками.
По аналогии с этим любой объект, созданный руками человека и движущийся вокруг данного небесного тела, называют искусственным спутником. Для вывода спутника на орбиту необходима работа мощных двигателей, но при движении спутника по постоянной орбите двигатели на спутнике выключены. Почему же он движется по орбите?
Чтобы ответить на данный вопрос, давайте рассмотрим упрощенную модель движения
искусственного спутника. Будем считать, что он движется с постоянной по модулю скоростью по круговой орбите вокруг данной планеты в безвоздушном пространстве и только под действием ее сил тяготения (рис. 85). Силами тяготения со стороны других космических тел можно пренебречь.
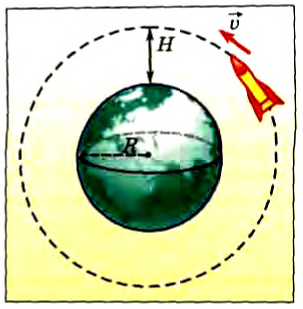
Рис. 85
Если нет сопротивления воздуха, а сила тяготения в любой момент перпендикулярна скорости движения, то создаваемое ею ускорение также перпендикулярно скорости и не может изменять ее модуль. Вот почему такой идеальный спутник должен бесконечно долго вращаться по своей орбите с выключенными двигателями. Реальные искусственные спутники Земли постепенно приближаются к ее поверхности, и в конце концов попадая в атмосферу, сгорают в ней.
Какова должна быть скорость спутника, чтобы он двигался по круговой орбите?
Определим эту скорость, считая, что спутник движется на высоте H над поверхностью однородной шарообразной планеты массы M и радиуса R. Так как движение происходит по окружности, то спутник имеет центростремительное ускорение:
которое ему сообщает сила тяготения:
Отсюда скорость движения спутника по орбите на высоте H над поверхностью:
Если использовать формулу для ускорения свободного падения вблизи поверхности планеты, то скорость спутника на высоте H от поверхности планеты равна:
Первой космической скоростью для планеты называется скорость, которую нужно сообщить спутнику, чтобы он двигался по круговой орбите вблизи поверхности планеты, т. е. 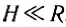
Тогда величина первой космической скорости определяется по формуле:
При движении спутников на высоте 200—300 км от поверхности Земли первая космическая скорость равна 7,9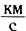
Из приведенных формул следует, что, чем выше над поверхностью планеты расположена орбита спутника, тем меньше его скорость и тем больше его период обращения. Спутники с космонавтами летают на высоте 200—300 км и облетают нашу планету меньше чем за полтора часа. Спутники связи расположены на большом удалении от поверхности, летят с меньшей скоростью, чем первая космическая скорость.
Вы, наверное, часто слышали, что в открытом космосе и на спутнике космонавты находятся в состоянии невесомости, а по телевизору наблюдали их как бы плавающие движения в космическом корабле (рис. 86). Космонавты и все предметы движутся вместе со спутником по орбите под действием только силы тяготения Земли, т. е. находятся в свободном падении.

Рис. 86
Возможно ли это: спутник свободно падает и в то же время остается на постоянной орбите? Примем для простоты расчетов, что ускорение свободного падения равно 10 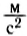
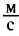
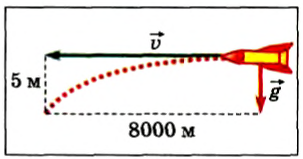
Рис. 87
Главные выводы:
- Движение искусственных спутников по орбите происходит только под действием силы тяготения.
- Скорость спутника на круговой орбите зависит от массы планеты, ее радиуса и высоты спутника над поверхностью планеты. Первая космическая скорость определяется только массой и радиусом планеты.
- Невесомость на спутнике объясняется тем, что в любой момент времени он движется с ускорением свободного падения для данной точки пространства.
Видео:Урок 79. Центр масс тела и методы определения его положенияСкачать

Сила упругости
Как вы уже знаете, одно из проявлений взаимодействия тел — их деформация, т. е. изменение формы и размеров, происходящее из-за неодинакового смещения различных частей одного тела в результате воздействия другого тела.
Почему деформации неодинаковы у различных тел? Какую роль они играют во взаимодействии тел и в механическом движении?
Чтобы ответить на первый вопрос, вспомним, что вы узнали о строении вещества при изучении физики в 8-м классе.
Все вещества состоят из частиц (молекул, атомов, ионов), между которыми существуют силы взаимодействия. Это силы электромагнитной природы, которые в зависимости от расстояния между частицами проявляются то как силы притяжения, то как силы отталкивания.
Если воздействие на тело вызывает увеличение расстояния между молекулами, то силы межмолекулярного притяжения препятствуют этому. Уменьшению расстояния между молекулами противодействуют силы отталкивания. Чтобы не рассматривать сложные электромагнитные взаимодействия, в механике для характеристики этих явлении вводят силу упругости 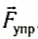
Силой упругости называется сила, возникающая при деформации любых твердых тел, а также при сжатии жидкостей и газов.
Какую роль играет эта сила при взаимодействии тел?
Проделаем следующий опыт. Возьмем толстый кусок поролона, нарисуем по его торцу горизонтальные линии на одинаковом расстоянии друг от друга, а затем, медленно опуская, поставим на него груз (рис. 88, а).
Если смотреть во время опускания груза на торец поролона, то хорошо видно, как при сжатии поролона под действием груза сближаются между собой линии, но лишь до определенного расстояния (рис. 88, б). Движение груза прекращается при некоторой деформации поролона, т. е. сила упругости уравновешивает силу тяжести.
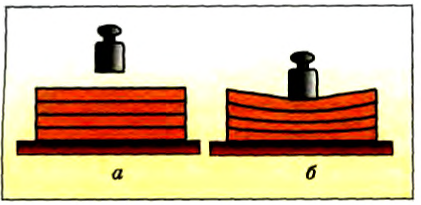
Рис. 88
Также же наблюдения можно провести, подвешивая груз на резиновой ленте с нанесенными на ней линиями. При подвешенном грузе расстояние между линиями на ленте больше.
Мы взяли для опытов поролон и резиновую ленту, потому что для этих тел под действием даже небольших сил наблюдается значительная деформация и ее легко наблюдать.
Аналогичные явления происходят при любых взаимодействиях тел, но часто деформации так малы, что их можно зафиксировать только с помощью очень чувствительных приборов.
Проведем еще один опыт (рис. 89, а). Прикрепим к бруску, лежащему на столе, резиновый шнур (с метками на одинаковом расстоянии друг от друга) и медленно начнем тянуть его в горизонтальном направлении.
Под действием силы шнур растягивается, и только когда весь шнур растянется на некоторую величину, брусок придет в движение. Как это объяснить?
При растяжении шнура происходит смещение одних его частей относительно других, в результате чего в шнуре возникает сила упругости, равная но величине деформирующей силе. C этого момента шнур играет роль «передающего звена» (рис. 89. б).
Такие же явления всегда происходят, когда движение от одного тела к другому передается при помощи «связей», т. е. нитей, шнуров, пружин, тросов, различных сцепок и т. п. 
Рис. 89
По характеру смещения частей тела (а вернее, молекулярных слоев внутри его) друг относительно друга различают деформации: растяжения, сжатия, изгиба, кручения, сдвига.
При деформации растяжения расстояние между молекулярными слоями увеличивается (рис. 90, а), а при деформации сжатия — уменьшается (рис. 90, б). Деформацию растяжения испытывают тросы подъемных кранов, канатных дорог, буксирные тросы, струны музыкальных инструментов. Сжатию подвергаются стены и фундаменты зданий.
Если в результате воздействия одни молекулярные слои растягиваются, а другие сжимаются, то наблюдается деформация изгиба (рис. 90, в). Деформацию изгиба испытывают балки перекрытий в зданиях и мостах.
При деформации кручения происходит поворот одних молекулярных слоев относительно других (рис. 90, г).
Если одни слои молекул смещаются относительно других, то происходит деформация сдвига (рис. 90, б).
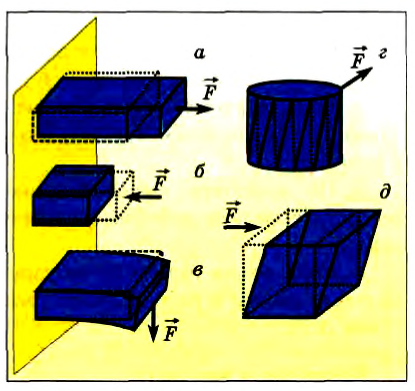
Рис. 90
Деформации также разделяют на упругие и неупругие, или пластичные.
Деформация называется упругой, если после прекращения воздействия тело полностью восстанавливает первоначальные форму и размеры, а если этого не происходит, то деформация называется неупругой или пластичной.
Конечно, деформация конкретного тела может быть как упругой, так и неупругой, так как ее характер зависит не только от свойств тела, но и от величины воздействия на него. Например, при больших воздействующих силах и стальная линейка потеряет форму, а при очень малых — и пластилин восстановит свою форму.
Главные выводы:
- Сила упругости возникает при изменении формы и размеров твердых тел, а также при сжатии жидкостей и газов.
- Силы упругости, возникающие в нитях, подвесах, опорах и других «связях>, обеспечивают передачу воздействия или движения от одного тела к другому.
- По характеру смещения молекулярных слоев друг относительно друга выделяют деформации: растяжения, сжатия, изгиба, кручения и сдвига.
- Деформации разделяют на упругие и пластичные по степени восстановления формы и размеров тела после прекращения действия деформирующей силы.
Видео:Дифференциальное уравнение движения материальной точки.Скачать

Закон Гука
Различные виды деформаций возникают в любых сооружениях и механизмax, и необходимо установить законы, которые позволят рассчитать величину тих деформаций.
Наиболее часто встречаются и достаточно просто математически описываются упругие деформации растяжения или сжатия.
Проведем опыт, прикрепив один конец резинового шнура с метками к вертикальной стенке, а другой — к динамометру (рис. 91, а), на который будем действовать силой. Расположим под шнуром линейку. Определяя силу, действующую на конец шнура, по динамометру, будем фиксировать смещение конца JHypa вдоль линейки и изменение расстояний между метками.
Мы заметим, что общее удлинение шнура, определяемое по смещению его конца, является суммой удлинений всех его частей. Аналогично общее укоронение, например при сжатии пружины, является суммой уменьшений расстояний между всеми ее витками (рис. 91,6).
Рис. 91
Если обозначить начальную длину шнура L0, а конечную длину — L, то для характеристики деформаций растяжения или сжатия можно ввести абсолютное удлинение △L = |L — L0|.
Если шнур под действием деформирующей силы 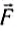
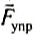
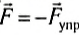
Роберт Гук установил экспериментально. что при малых деформациях растяжения или сжатия абсолютное удлинение тела прямо пропорционально деформирующей силе. На практике часто необходимо определить силу упругости, возникающую в теле при его деформации, и закон Гука формулируется следующим образом:
модуль силы упругости, возникающей при малых деформациях сжатия или растяжения тела, прямо пропорционален величине абсолютного удлинения:
где k — коэффициент пропорциональности, называемый жесткостью тела.
Жесткость является характеристикой данного тела (пружины, шнура, стержня и т. п.) и зависит от его поперечных и продольных размеров, химического состава и строения вещества, из которого тело изготовлено. Так как 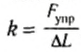
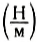
При расчетах движения тел под действием силы упругости необходимо учитывать ее направление. Если выбрать начало отсчета под крайней точкой недеформированного тела (рис. 92), то абсолютное удлинение можно характеризовать координатой х конца деформированного тела. При растяжении (см. рис. 92, а) и при сжатии (см. рис. 92, б) образца сила упругости направлена противоположно смещению его конца. Тогда можно записать закон Гука для проекции силы упругости на выбранную ось:
Ту или иную форму записи закона Гука используют в зависимости от условия задачи и величины, которую нужно определить. Сила упругости, как и любая из сил, рассматриваемых в механике, подчиняется законам Ньютона, а по закону Гука можно рассчитать деформации, возникающие при взаимодействиях тел. Однако необходимо отметить, что закон Гука хорошо выполняется только при малых деформациях тел.
Главные выводы:
- При упругих деформациях растяжения и сжатия абсолютное удлинение прямо пропорционально деформирующей силе.
- При упругих деформациях сила упругости прямо пропорциональна абсолютному удлинению.
- Жесткость тела зависит от его поперечных и продольных размеров, химического состава и строения вещества, из которого изготовлено тело.
Механические свойства тел
Для строительства зданий, мостов, самолетов, автомобилей необходимо знать механические свойства используемых материалов: дерева, бетона, стали, алюминия и т. п. Нужно также учитывать поведение этих веществ при больших деформациях, способных привести к разрушениям.
При деформации по всему объему тела возникают упругие силы, т. е. тело находится в напряженном состоянии. Для характеристики этого состояния вводят механическое напряжение — физическую величину, равную отношению модуля силы упругости к площади поперечного сечения тела:
Эта величина численно равна силе упругости, возникающей в единичном сечении тела, и измеряется в ньютонах на квадратный метр 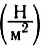
На практике вы сталкивались с тем, что абсолютное удлинение зависит от начальных размеров тела, например, под действием одной и той же силы длинный резиновый шнур растягивается больше, чем короткий (рис. 93).
Поэтому вводят относительное удлинение: 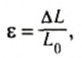
которое показывает, на какую долю первоначальной длины тела изменяется каждая ее единица. В некоторых случаях относительное удлинение выражают в процентах.
Рис. 93
При исследовании растяжений различных тел было обнаружено, что наблюдается сложная зависимость напряжения от относительного удлинения тела, называемая диаграммой растяжения (рис. 94). Обсудим, какие процессы в деформируемом теле отражают различные участки этой диаграммы.
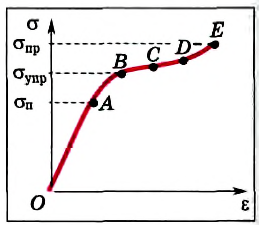
Рис. 94
На участке OA напряжение прямо пропорционально относительному удлинению, и если воздействие прекратилось, то тело восстанавливает свою форму и размеры, т. е. происходит упругая деформация. На практике такая зависимость наблюдается при небольших относительных деформациях и только до определенного напряжения σn, которое называется пределом пропорциональности.
На участке AB такая зависимость нарушается, но до некоторого напряжения, называемого пределом упругости σynp: после прекращения воздействия размеры и форма тела полностью восстанавливаются.
При напряжениях, превышающих предел упругости, наблюдается пластичная деформация (участок BD). На участке CD деформация происходит почти без увеличения напряжения. Это явление называется текучестью материала, а образцы, для которых область текучести велика, могут без разрушения выдерживать большие деформации.
Материалы, у которых область текучести почти отсутствует, являются хрупкими. Они разрушаются даже при небольших деформациях. Хрупкость характерна для стекла, кирпича, бетона, чугуна.
Точка диаграммы E соответствует напряжению, называемому пределом прочности σпp, при дальнейшей деформации образец разрушается.
Зависимость, отраженная на диаграмме участком OA. соответствует закону Гука в другой форме:
механическое напряжение в упруго деформированном теле прямо пропорционально относительной деформации: 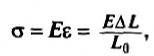
где E — модуль продольной упругости, который в честь ученого Томаса Юнга называется модулем Юнга и является характеристикой вещества, из которого сделано тело. Так, модуль продольной упругости живого дерева (рис. 95) больше, чем сухого дерева (рис. 96). Так как относительная деформация безразмерная величина, то модуль Юнга измеряется, как и механическое напряжение, в паскалях (Па).
 Рис. 95 |  Рис. 96 |
Как видно из формулы, модуль Юнга численно равен напряжению, возникающему в теле при относительной деформации, равной единице, т. е. при увеличении длины образца вдвое, так как при 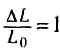
Если использовать соответствующие формулы для напряжения и относительного удлинения, то установленную зависимость для модуля силы упругости можно записать следующим образом:
Сравнив с записью закона Гука, получим выражение для жесткости: 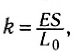
которое поясняет зависимость жесткости тела от его начальных размеров и свойств вещества.
Для некоторых тел, например стержней, нитей, тросов, при небольших деформациях площадь поперечного сечения практически остается постоянной, и закон Гука для модуля силы упругости можно использовать в форме:
Модуль упругости и предел прочности различных веществ можно узнать в справочниках.
Главные выводы:
- Механическое напряжение вводится для характеристики сил упругости, возникающих в теле.
- Для различных тел на опыте установлена сложная зависимость механического напряжения от относительной деформации, называемая диаграммой напряжения.
- Модуль упругости вещества определяется его химическим составом и строением.
Силы сопротивления движению
Как вы уже знаете, взаимодействие различных тел может либо вызывать движение конкретного тела, либо препятствовать ему. Например, если мы дуем в сторону легкого листа бумаги на столе, то заставляем двигаться воздух, а тот, в свою очередь, приводит в движение бумагу. Если мы поднимем тот же лист и отпустим, то он начнет двигаться под действием силы тяжести, а воздух будет препятствовать этому движению (рис. 97).
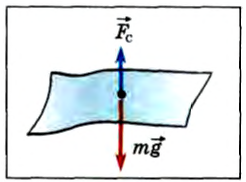
Рис. 97
На практике все силы сопротивления движению разделяют на силы сухого (внешнего) трения (покоя, скольжения и качения), которые возникают при взаимодействии соприкасающихся твердых тел друг с другом, а также силы вязкого трения, проявляющиеся при движении тела в жидкости или газе.
Рассмотрим на опыте, как проявляется и от чего зависит сила трения покоя. К бруску, лежащему на горизонтальной поверхности, прикрепим динамометр, на который будем действовать в горизонтальном направлении (рис. 98).
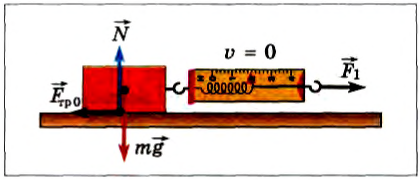
Рис. 98
Потянем слегка за динамометр, но так, чтобы брусок оставался в покое. Отметим показание прибора и проанализируем результаты нашего действия.
Так как брусок покоится, то по второму закону Ньютона векторная сумма всех сил, действующих на него, равна нулю. Сила тяжести уравновешивается силой упругости стола в вертикальном направлении.
Следовательно, и в горизонтальном направлении воздействие динамометра на брусок должно быть компенсировано какой-то силой. При изучении физики в 7-м классе вы узнали, что так проявляется сила трения покоя 
Под микроскопом на поверхности любого твердого тела хорошо видны разнообразные выступы и впадины (рис. 99).
рис. 99
Многочисленные неровности соприкасающихся поверхностей цепляются друг за друга, деформируются и препятствуют относительному перемещению тел. Кроме того, расстояние между молекулами, расположенными на выступах соприкасающихся поверхностей, мало, и поэтому возможно электромагнитное взаимодействие молекул.
Все эти сложные взаимодействия в механике характеризуются силой трения покоя, или силой трения сцепления.
Уменьшится ли сила трения покоя, если отшлифовать поверхность тел? Да, уменьшится, но только до определенной степени шлифовки, а при дальнейшей обработке сила трения покоя возрастает. Это происходит потому, что по мере сглаживания неровностей соприкасающихся поверхностей в значительной мере увеличивается число межмолекулярных взаимодействий.
Продолжим опыт, постепенно увеличивая силу воздействия. Показания динамометра увеличиваются, а тело еще покоится, следовательно, и сила трения покоя тоже возрастает. В этом основная особенность силы трения покоя.
Сила трения покоя равна по модулю и направлена противоположно силе, приложенной к покоящемуся телу параллельно поверхности соприкосновения его с другим телом:
Если еще увеличивать действующую силу, то при определенном показании динамометра тело начнет двигаться. Это значит, что существует определенная максимальная сила трения покоя, и действующая сила должна ее превысить, чтобы тело приобрело ускорение.
Вы знаете, что наиболее трудно на практике сдвинуть с места тяжелые предметы. Давайте выясним, почему это так.
Поставим на брусок добавочный груз и измерим максимальную силу трения покоя (рис. 100). Ее численное значение увеличивается. При добавлении еще одного груза сила трения покоя вновь возрастает.
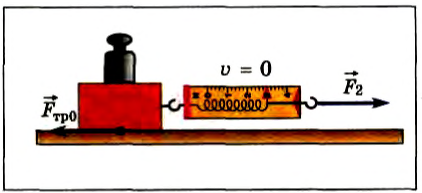
Рис. 100
Снимем с бруска грузы и подействуем на него добавочной силой вертикально вниз (рис. 101). Сила трения покоя также увеличивается. Как объяснить эти опыты?
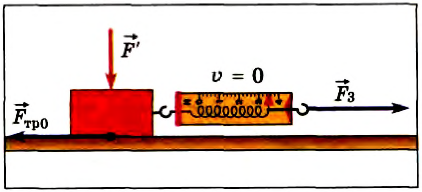
Рис. 101
При добавлении грузов, как и при воздействии вертикальной силой, увеличивается сила давления бруска на опору. Опыт показывает, что модуль максимальной силы трения покоя прямо пропорционален силе давления тела на опору:
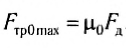
Где μ0 — коэффициент трения покоя, F1 — сила давления тела на опору.
Коэффициент трения покоя зависит от веществ, из которых изготовлены соприкасающиеся тела, и степени обработки их поверхностей.
Сила трения покоя удерживает тело, лежащее на наклонной плоскости (рис. 102), а также брусок, прижимаемый к вертикальной стене (рис. 103). Чем тяжелее брусок, тем больше должна быть сила трения покоя, чтобы уравновешивать силу тяжести. Поэтому тяжелый брусок приходится прижимать к стене со значительной по модулю силой.
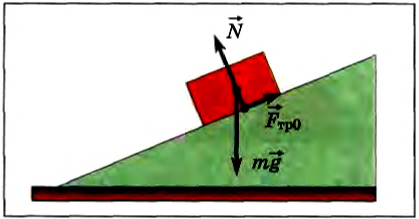 Рис. 102 | 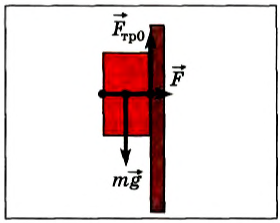 Рис. 103 |
По третьему закону Ньютона 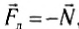
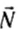
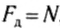
Возникает вопрос: всегда ли сила трения покоя препятствует движению? Нет, не всегда. Во многих случаях сила трения покоя способствует движению.
Например, кирпич, неподвижно лежащий на ленте транспортера, движется вместе с ней, потому что на него со стороны ленты действует сила трения покоя (рис. 104).
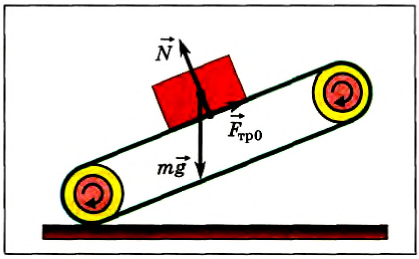
Рис. 104
Ведущее колесо автомобиля, если не пробуксовывает, действует на опору против направления движения с силой 
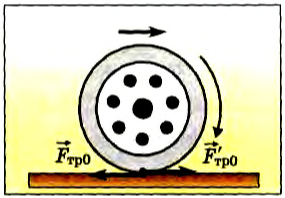
Рис. 105
При ходьбе сила трения покоя дает возможность человеку толкнуть опору с некоторой силой. По третьему закону Ньютона на человека действует такая же по величине и противоположная по направлению сила.
Трение покоя позволяет человеку брать руками различные тела, например топор, лопату, руль велосипеда или автомобиля, а также управлять движением этих тел, использовать их для совершения работы.
Главные выводы:
- Сила трения покоя (сцепления) всегда направлена параллельно поверхности соприкосновения двух тел и противоположно силе, стремящейся вывести это тело из состояния покоя.
- Модуль силы трения покоя может быть различен и в данный момент равен модулю силы, стремящейся вывести тело из состояния покоя.
- Максимальная сила трения покоя, действующая на тело со стороны опоры, прямо пропорциональна силе нормального давления тела на данную опору.
Силы трения скольжения и качения
Термин «скольжение» в физике используется для описания движения одного тела по поверхности другого тела.
Рассмотрим равномерное движение бруска по горизонтальной поверхности доски (рис. 106), т. е. его скольжение по опоре. Мы действуем с определенной горизонтальной силой на динамометр, а он передает наше воздействие бруску и показывает модуль действующей на брусок силы. Если скорость бруска постоянна, то силу, вызывающую движение, должна компенсировать сила взаимодействия бруска с опорой.
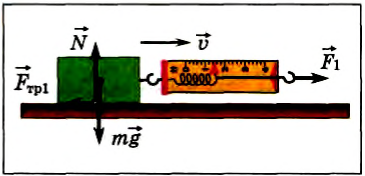
Рис. 106
При изучении физики в 7-м классе вы узнали, что эта сила называется силой трения скольжения. Она возникает из-за электромагнитного взаимодействия молекул на неровностях соприкасающихся поверхностей, зацепления неровностей и их пластичной деформации при относительном движении тел.
Из эксперимента следует, что сила трения скольжения, действующая на тело, направлена противоположно направлению его движения. По третьему закону Ньютона на опору при движении тела действует сила трения скольжения Eτp, направленная в сторону движения тела.
Поместим на брусок груз такой же массы и будем тянуть горизонтально динамометр так, чтобы брусок с грузом двигался равномерно (рис. 107). Динамометр при этом покажет вдвое большую силу. Если еще увеличить массу бруска, то сила трения скольжения также возрастет.
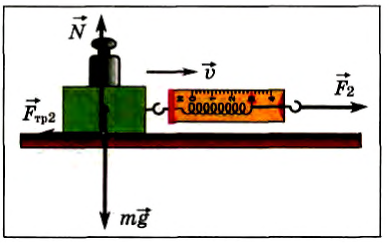
Рис. 107
Опыты показывают, что модуль силы трения скольжения прямо пропорционален модулю силы нормального давления:
где μ — коэффициент трения скольжения. Так как по третьему закону Ньютона Fд = N, то можно записать
Рассмотрим равномерное движение бруска с грузом по другой стороне доски, более шероховатой (рис. 108). При постоянной скорости движения динамометр показывает большую силу, хотя сила нормального давления не изменилась. Значит, изменился коэффициент трения скольжения, и именно он зависит от качества обработки соприкасающихся поверхностей.
Если заменить доску листом стекла или другого материала, то показания динамометра снова изменятся, т. е. коэффициент трения зависит от свойств обоих веществ соприкасающихся поверхностей.
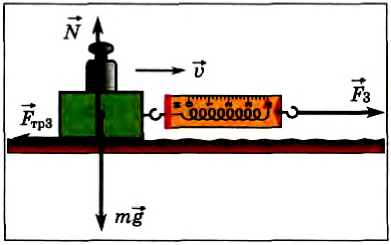
Рис. 108
Однако опыт показывает, что коэффициент трения не зависит от относительного положения тел. Например, коэффициент трения льда по железу такой же, как и железа при скольжении по льду.
Зависит ли коэффициент трения от площади соприкосновения тел? Если сравнить показания динамометра при равномерном движении бруска в различных положениях (рис. 109), то оказывается, что показания во всех трех случаях совпадают, т. е. коэффициент трения не зависит от площади соприкосновения тел.
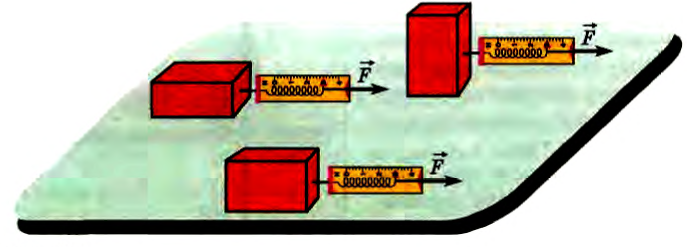
Рис. 109
Вы знаете из личного опыта, что сдвинуть тело с места труднее, чем перемещать его с постоянной скоростью. Многочисленные эксперименты показывают, что действительно при движении с малыми скоростями величина силы трения скольжения немного меньше величины максимальной силы трения покоя и практически не зависит от скорости тела.
Это объясняется тем, что коэффициент трения скольжения в большинстве случаев немного меньше коэффициента трения покоя. Так как различия невелики, то при решении задач коэффициенты трения принимают равными по величине и обозначают одной буквой μ. Поэтому силу трения скольжения в большинстве задач считают постоянной и приближенно равной максимальной силе трения покоя.
Одним из достижений в истории человечества считается изобретение несколько тысяч лет назад такого привычного для нас колеса. Если вращающиеся колесо или шар участвуют и в поступательном движении по какой-то поверхности, то возникает сила сопротивления движению, которую называют силой трения качения. Чтобы объяснить причины ее возникновения, рассмотрим качение тяжелого цилиндра по куску поролона, деформация которого при этом хорошо наблюдается (рис. 110).
Цилиндр соприкасается с поролоном на очень малой площади, а значит, оказывает на него достаточно большое давление. Поролон при этом деформируется.
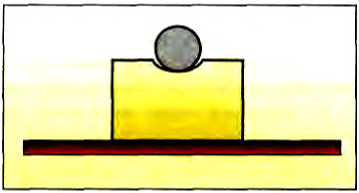
Рис. 110
Вследствие этой деформации перед катящимся цилиндром возникает как бы горка. Для характеристики этого явления в механике вводят силу трения качения.
Чем более пластична возникающая деформация, тем больше сила трения качения. Если цилиндр катится по такой поверхности, что ее деформация упруга и незначительна, то сила трения качения невелика. Она во много раз меньше силы трения скольжения, которая возникала бы только при поступательном движении этого же тела.
В таких случаях при относительном движении тел выгоднее скольжение заменить качением, и поэтому используют колеса для транспорта и подшипники в различных механизмах.
Если при движении происходит значительная деформация тела и опоры или только опоры, то сила трения качения велика, и поэтому, например, зимой у телеги заменяют колеса на полозья.
Главные выводы:
- Сила трения скольжения препятствует движению, всегда направлена противоположно относительной скорости тела.
- Модуль силы трения скольжения прямо пропорционален модулю силы нормального давления тела на опору.
- Коэффициент трения скольжения зависит от свойств веществ соприкасающихся поверхностей, степени их обработки и не зависит от взаимного расположения поверхностей и площади их соприкосновения.
- Сила трения качения намного меньше силы трения скольжения, если деформации взаимодействующих при движении тел очень малы.
Вязкое трение
При движении твердого тела в жидкости или газе также возникает сила сопротивления движению, которую в этих случаях называют силой жидкого или вязкого трения.
Экспериментально установлено, что сила, действующая на движущееся тело в жидкости или газе, также направлена в сторону, противоположную движению, но численно она во много раз меньше силы трения скольжения при небольших скоростях движения.
В отличие от сухого трения для тела в жидкости или газе отсутствует сила трения покоя и даже самая маленькая сила, приложенная к телу, вызывает его движение, если этому не препятствуют другие силы. Следовательно, сила вязкого трения не противодействует возникновению движения, и поэтому в механизмы вводят разнообразные смазки для движущихся друг относительно друга частей.
Проведем опыт. Возьмем два одинаковых тетрадных листа и отпустим в горизонтальном положении с одной высоты (рис. 111, а). Листы плавно и почти одновременно упадут на пол. Сделаем из одного листа плотный и маленький комок, а другой лист просто сомнем и повторим опыт. Первым упадет маленький комок (рис. 111, б). Как вы думаете, почему, ведь массы листов одинаковы?
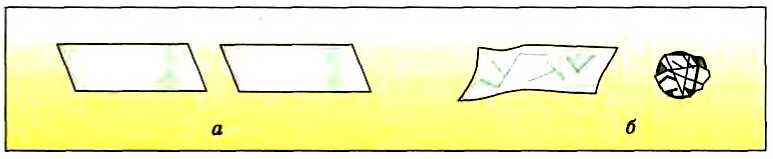
Рис. 111
Да, вы правы, сопротивление воздуха движению тел зависит от их формы и размеров. На рисунке 112 показаны тела различной формы: диск, шар и каплеобразное тело, у которых площади одного из поперечных сечений одинаковы.
При движении этих тел в жидкости или газе в направлении, перпендикулярном этому сечению, наибольшая сила вязкого трения действует на плоскую шайбу, а наименьшая — на тело каплеобразной формы.
Рис. 112
Форму тела, при которой сила вязкого трения (сопротивления) мала, называют обтекаемой и ее стараются придать телам, движущимся в жидкости или газе. Обтекаемую форму имеют ракеты и самолеты, подводные лодки и скоростные автомобили.
Установлено, что сила вязкого трения зависит от скорости движения тела. При малых скоростях ее модуль прямо пропорционален скорости движения тела относительно среды:
Где k1 — коэффициент сопротивления, зависящий от формы, размеров тела, состояния его поверхности и свойств среды.
При больших скоростях движения модуль силы сопротивления пропорционален квадрату скорости:
Это объясняется тем, что при большой скорости тела возникают сложные движения слоев среды. и поэтому появляется добавочное сопротивление.
Качественный график зависимости проекции силы сопротивления на направление скорости от модуля скорости представлен на рисунке 113. Сила сопротивления всегда направлена противоположно скорости. Если скорость невелика, то сила сопротивления линейно зависит от скорости, а при больших скоростях график имеет вид параболы.
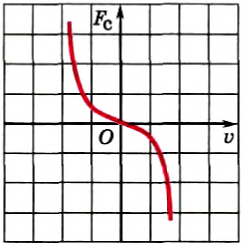
Рис. 113
Следовательно, при ускоренном движении тела в жидкости или газе, на пример под действием силы тяжести, вместе с ростом скорости растет и сила вязкого трения. При некотором значении скорости тела сила вязкого трения становится равной его силе тяжести, и затем тело движется с установившейся скоростью, тем большей, чем больше сила тяжести тела.
Например, размеры и форма парашюта подбираются с таким расчетом, чтобы скорость установившегося движения была безопасной для человека при его приземлении — около 6 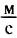
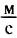
Учет всех сил сопротивления на практике достаточно сложен, поэтому при решении задач нужно внимательно прочесть условие и оценить, какой вид трения необходимо учесть и каким в данных условиях можно пренебречь.
Главные выводы
- Сила вязкого трения при малых скоростях пропорциональна модулю скорости, а при больших — квадрату модуля скорости тела.
- Сила вязкого трения зависит от формы тела. Форму тела, при которой сила сопротивления движению (вязкого трения) минимальна, называют обтекаемой.
- Сила вязкого трения, как правило, много меньше силы трения скольжения, и поэтому в различных механизмах используют смазку.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Сила тяжести в физике
- Сила упругости в физике и закон Гука
- Деформация в физике
- Плотность вещества в физике
- Звуковые и ультразвуковые колебания
- Инерция в физике
- Масса тела в физике
- Сила в физике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎦 Видео
Урок 39 (осн). Сила трения. Коэффициент тренияСкачать

Урок 33 (осн). Сила тяжестиСкачать

13.2. Определение параметров прямолинейного движения по заданным силамСкачать

Математика это не ИсламСкачать

ДВИЖЕНИЕ ПО НАКЛОННОЙ ПЛОСКОСТИ | механика 10 классСкачать

Как ПРАВИЛЬНО решать задачи по физике?Скачать

Д1 Дифференциальные уравнения движения материальной точкиСкачать

Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать

Первая основная задача динамики. Задачи 1, 2, 3, 4Скачать

Основное уравнение динамики вращательного движения. 10 класс.Скачать



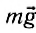
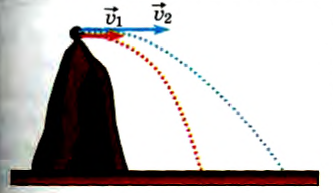
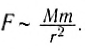
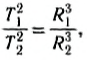
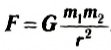
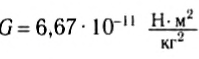
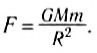
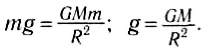
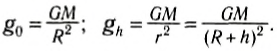
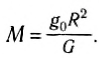
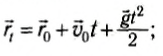
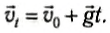
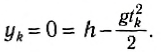
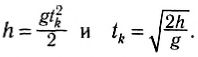
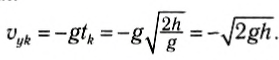
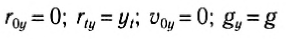
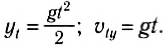
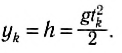
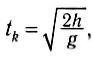
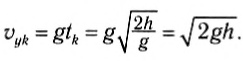
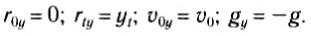
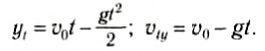
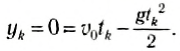
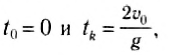
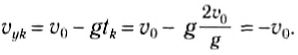
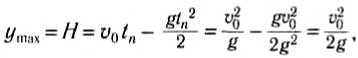
 .
.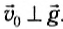
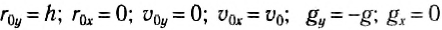
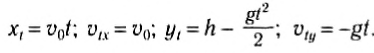
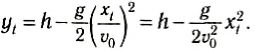
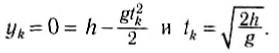
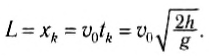
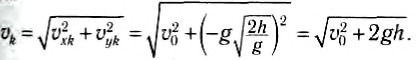
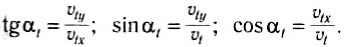
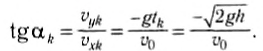
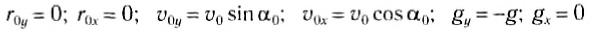
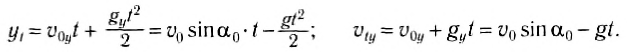
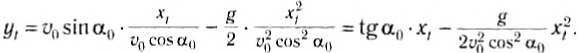
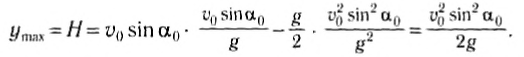
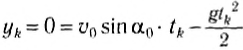
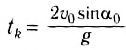
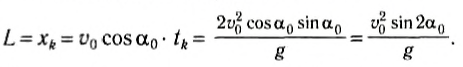
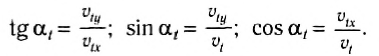
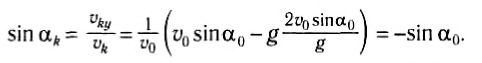
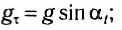
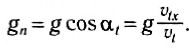
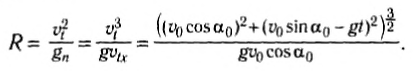
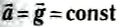 вдоль вертикального направления и равномерного вдоль горизонтального направления.
вдоль вертикального направления и равномерного вдоль горизонтального направления.