По какой из формул можно найти все корни уравнения sinx a где a 1 (7 видео)

Уравнение. Простейшее тригонометрическое уравнение sin х = а.

Существует возможность отобразить всякий корень уравнения sin х = а, как абсциссу некой точки пересечения синусоиды у =sinх и прямой у = а, и, соответственно верно обратное, абсцисса всякой такой точки пересечения выступает одним из корней уравнения.

При | а| >1 синусоида у = sin х не пересечется с прямой у = а. В данном случае у уравнения нет корней.

При а = 0 у уравнение sin x = а будут корни:

где m изменяется по всем целым числам (m = 0, ±1, ±2, ±3, . ).

Несомненно, arcsin0 = 0 и соответственно получаем (-1) m arcsin 0 + mπ = mπ.

При а = 1, корни уравнения определяются по формуле:

где k изменяется по всем целым числам (k = 0, ±1, ±2, ±3, . ).

Для обоснования формулы выполним подстановку: а = 1 в формулу:

(-1) m arcsin0+ mπ = mπ и принимая к сведению, что arcsin 1= π /₂, имеем: (- 1) m arcsin 1 + mπ= (- 1) mπ /₂ + mπ.

где k изменяется по всем целым числам (k = 0, ±1, ±2, ±3, . . .).

Необходимо учитывать, что все вышеуказанные формулы можно применять в том случае, когда искомый угол х представлен в радианах. Когда х представлен в градусах, то эти формулы нужно преобразовать.

К примеру, вместо формулы (-1) m arcsin 0 + mπ = mπ необходимо применять формулу х= (-1) m arcsinа + 180m, вместо формулы х = mπ — формулу х= 180 m и т. д.

Содержание

Решение уравнения sin x = а
Как репетитор по математике поясняет формулу корней уравнения SinX=a
Какую коррекцию проводит репетитор по математике?
🎥 Видео

Видео:Отбор корней по окружностиСкачать

Решение уравнения sin x = а

Корни уравнения sin(x) = a, -1 ⩽ a ⩽ 1 выражаются формулой x = (-1)arcsin(a)+πn, n ∈ Z.

Примечание: Очевидно, что уравнение sin(x) = a не имеет решений, если а не входит в промежуток [-1;1], то есть |a| ⩽ 1

Попробуем разобраться, почему, решения выражаются этой формулой.

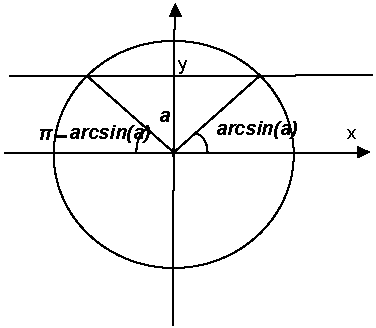
Начертим координатную плоскость и тригонометрическую окружность. Синус, по определению,- это ордината точки пересечения окружности единичного радиуса с центром в начале координат и луча, выходящего из начала координат и составляющего с осью ОХ угол а. Начертим множество всех точек, ординаты которых равны а – это будет прямая y = a. Прямая пересечет окружность в двух точках.

Один из углов, соответствующих этой точке будет иметь величину arcsin(a). Этой же точке будет соответствовать и угол arcsin(a)+2π, и угол arcsin(a)+4π, и угол arcsin(a)+6π и т.д.

Все вместе это можно выразить формулой x = arccos(a)+2πn, n ∈ Z.

Один из углов, соответствующих второй точке, будет иметь величину π-arcsin(a). Этой же точке будет соответствовать и угол π-arcsin(a)+2π, и угол π-arcsin(a)+4π, и угол π-arcsin(a)+6π и т.д.

Все вместе это можно выразить формулой x = π-arcsin(a)+2πk, k ∈ Z.

Объединение этих двух формул дает формулу x = (-1)arcsin(a)+πn, n ∈ Z.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Видео:Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

Как репетитор по математике поясняет формулу корней уравнения SinX=a

Известно, что большинство школьных учебников по математике далеко от методического совершенства, к которому так стремятся их авторы. На мой взгляд, многие из них предлагают туманные или совсем точные объяснения сложных теоретических вопросов. Обычно, если репетитор по математике в совершенстве владеет искусством объяснений, то либо меняет логику учебника полностью, либо дополняет тексты адаптированными для детского восприятия комментариями. Я уже давно пересмотрел подходы к изучению многих тем школьной программы по математике, являющиеся классическими. Невнятная логика переходов от одного факта к другому (от формулы к формуле), сухая схематичность выкладок и обилие математических терминов, — далеко не полный список проблем в построении классических объяснений.

Можно ли как-то исправить недосмотры и переписать учебники с учетом этих замечаний? Думаю, что нельзя. Почему? Если аккуратно подходить к каждому проблемному участку и менять «скупую математику» на «живую» и понятную, то размеры учебников возрастут в несколько раз. Почему? Очень трудно передать коротко те мысли, которые помогают прояснить сложные математические процессы. На некоторые из них придется потратить по 0,5-1,5 страниц печатного текста. Если так править каждый параграф, то и без того увесистые портфели учеников можно будет использовать для занятий тяжелой атлетикой.

Поэтому репетитор по математике как всегда «принимает огонь на себя». Отмечу, что индивидуальные занятия с преподавателем создают наилучшие условия для проникновения в глубины предмета, ибо в переполненном классе сложнее настроить ученика на серьезную вдумчивую работую. Репетитору же, как правило, удается донести до его сознания разного рода тонкости.

Толковое подробное объяснение сложного вопроса может отнять весь урок. И даже это не гарантирует 100%-го понимания темы всеми учащимися. Очень трудно удерживать внимание целой аудитории на детальном рассмотрении важных «мелочей». Особенно если оно долгое. Отдельно взятый ученик может в любой момент отвлечься от доски и полностью выключится из процесса. Преподаватель замеввший его потерянный взгляд и повторяющий часть объяснения заново, рискует запутает других учеников, ибо теряется последовательность изложения логических выводов. Сильному ученику станет скучно и он, скорее всего, потеряет концентрацию.

Неравномерность скорости восприятия информации (даже в классе с приблизительно равным уровнем знаний и способностей) делает аккуратные объяснения тем малоэффективными. Поэтому и здесь индивидуальный репетитор по математике оказывается в более выгодных условиях по сравнению со школьным преподавателем. В тихой и спокойной обстановке при полном контроле за пониманием и вниманием ученика репетитору удается объяснить теорему так, как это не удается сделать в классе.

Какую коррекцию проводит репетитор по математике?

Предлагаю вашему вниманию пример одного из моих объяснений при работе с темой «решение простейших тригонометрических уравнений». Напомню, что подготовка к ЕГЭ по математике включает в себя разбор формул для понимания решений задач типа С1. Что предлагает нам базовый учебник математики А.Н. Колмогорова 10-11 класс? Откроем пункт №9.2, стр.72 (17-е издание). В нем описывается построение формулы корней уравнения вида . Сделан рисунок круга и даны вполне нормальные объяснения формулам для левой и правой точек – концов соответствующей хорды.
где
Далее следует текст (цитирую): Удобно эти решения уравнения записывать не двумя, а одной формулой:
Нетрудно убедиться, что при четных k=2n из формулы (6) находим все решения, записанные формулой (4), а при нечетных k=2n+1 – решения, записываемые формулой (5).

Ну как Вам, понятно? Можно ли считать переход доказанным? Достаточно ли репетитору по математике повторить этот текст на уроке? Думаю, что нет. И вряд ли поможет прямая подстановка выражений 2n и 2n+1, ибо она точного доказательства не даст. Меня всегда возмущала тактика ухода от рассмотрения тонких вопросов. Как только автор с ним сталкивается, он сразу же прибегает к фразе «нетрудно убедиться» или «нетрудно доказать». Давайте разберемся, что именно здесь требуется вообще доказать и какие пояснения репетитору по математике следует предоставить ученику.

Пояснения репетитора к выводу формулы

Лучше строить рассуждения от обратного. Не подставлять 2n и 2n+1, а выделять их в 4-ой и 5-ой формулах. Некоторым ученикам 10 класса репетитор по математике должен объяснить принцип работы самих формул: для каждого целого числа, подставленного вместо буквы n (я использую всегда самые доступные фразы и термины) каждая формула вычисляет соответствующий ему угол. Подставляя в n все целые знания можно вычислить все множество углов (корней уравнения). Естественно, что запись формул может быть совершенно произвольной, когда множество сохраняется. Если замена на 6-ю формулу не приведет ни к потере, ни к приобретению лишних углов, то эта замена будет корректной. Согласно всем математическим правилам репетитору требуется просто показать совпадение множеств. Как это сделать? Лучше всего подготовить (преобразовать) формулы (4) и (5) к виду, максимально близкому к виду (6).

Понятно, что если вместо коэффициента «единица» перед арксинусом в формуле (4) поставить степень , то это не изменит результата при вычислении каждого угла, поскольку 2n – четно. В пятой формуле репетитор по математике переставляет слагаемое в конец выражения и выносит его за скобку. Это тождественное преобразование, также не меняющее результата при любом n. Затем вместо коэффициента -1 перед вторым арксинусом репетитор вставляет степень . И в этом случае результат сохранится, ибо при любом целом n значение 2n+1 будет нечетным, а при возведении 2n+1 в нечетную степень получим ту же самую «минус единицу».

Итак, репетитор по математике преобразует формулы к следующему виду:

Множители в последнем слагаемом специально переставляются, дабы обеспечить максимально точное расположение выражений 2n и 2n+1 для формулы (6) к моменту из замены на k. Лучше всего их выделить разным цветом.

Далее – самое важное. Текст репетитора (дословно):
Докажем, что каждый угол, вычисляемый по (4) формуле, можно вычислить по формуле (6). Почему? Допустим, в формулу (4) вставилось какое-нибудь целое число, например n=7. Тогда в зеленой рамке получится 14. Если вставить 14 вместо переменной k в формулу (6), то получим те же действия, что и в (4) и, следовательно, совпадут результаты. Очевидность этого совпадения обеспечивает максимально близкий вид 4-ой формулы к 6-ой. Поэтому ни один угол формулы (4) не будет потерян. Аналогичные рассуждения репетитор по математике проводит с формулой (5). Итак, мы гарантируем, что все углы формул (4) и (5) можно вычислить по формуле (6).

И наоборот, любой угол формулы (6) можно получить или по (4) или по (5). Почему? Допустим, что при каком-нибудь значении мы нашли угол по (6). Если k – четно, например k=10, то вставляя в 4-ю формулу n=5, мы вычислим тот же угол. Если k — нечетно, например (и здесь репетитору по математике лучше использовать примеры с конкретными значениями n), то подставляя n=6 в (5) снова увидим повторение набора действий и, как следствие, ответа. И так для любого числа k. Поэтому ни один угол формулы (6) не будет посторонним а оба множества (4)+(5) и (6) совпадут.

Если проводится подготовка к ЕГЭ по математике, то репетитору следует помнить о том, что в С1 наибольшую частоту появления имеют задачи на отбор корней. В этом случае общая формула, о которой идет речь в статье, не используется вовсе. Абитуриент отмечает точки на круге, удовлетворяющие условию SinX=a, отсекает лишнюю и только после этого записывает ответ. Думаю, что в условиях экспресс подготовки к ЕГЭ по математике не стоит тратить время на отработку навыков работы с «минус единицей в степени эн» и ограничиться сериями (4) и (5). Если абитуриент на ЕГЭ запишет ответ в С1 отдельными формулами, вместо общей, то это не приведет к снижению оценки (балла) за все задание.

Колпаков А.Н. Репетитор по математике Москва. Автор подхода.

Разумно, но какие-такие «математические правила» не убеждают, что общая формула есть объединение для четных и нечетных и наоборот? И уж очень длинное обсуждение совершенно очевидного факта!
А честно «доказать», что (-1)*(-1)=1, учителя и большинство репетиторов не сумеют, да еще будут отмазываться тупым возражением — «по определению»…

Речь шла о самых обычных правилах доказательства совпадения двух множеств. А совпадает с В, если любой элемент из А лежит в В и, наоборот, любой элемент из В лежит в А. Теперь по поводу очевидности. Надо понимать, что очевидный для репетитора (или для сильного десятиклассника) факт, далеко всегда очевиден слабому ученику, о подаче материала которому как раз и идет речь в статье. По уму — вообще вся школьная математика состоит из «совершенно очевидных фактов». Только почему-то дети воспринимают их по-разному. Рад за то, что Ва очевидны формулы. Но это Вам очевидно. А другому человеку? Репетитор должен уметь смотреть на математику глазами школьника, моделируя у себя в голове его мысли. Математик и репетитор — несколько разные профессии. Вы смотрите на триг. формулы глазами математика, а мне приходится смотреть на них глазами репетитора. Методика — это наука о том, как добиться наилучших результатов в понимании и закреплении материала большей части класса, в которой, как правило, процент сильных детей невысок. На практике репетитору довольно часто приходится разжевывать простейшее, иначе не добиться понимания фактов у определенной категории учащихся.

Мне кажется ученикам не понятно когда в ходе объяснения используется числовая окружность, не проще использовать график функции. А если кто-то не понимает что за корень с -1 в степени н, то можно просто ответ записывать в виде двух корней. Потом поймут что это одно и то же.

Во-первых, на графике не видна причина периодичности синуса и косинуса. Слишком он оторван от определения, которое формулируется на координатах ТОЧЕК КРУГА. Во-вторых, репетитору по математике будет сложнее объяснить и, соответственно, научить использовать длину периода. В-третьих, на графике практически невозможно показывать пересечения корней разных уравнений (если это потребуется). Его преимущество состоит только в лучшей демонстрации бесконечности множества корней изучаемых уравнений.