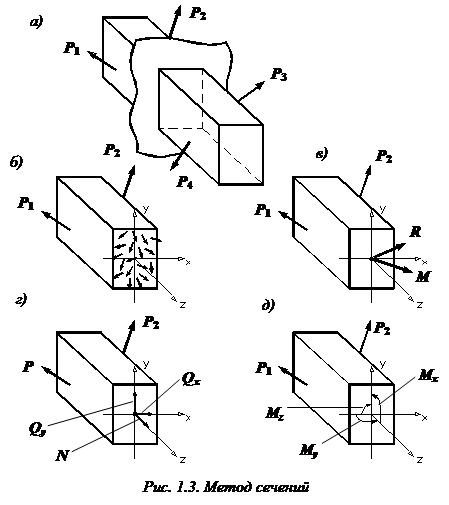
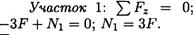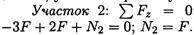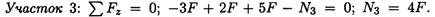Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки.
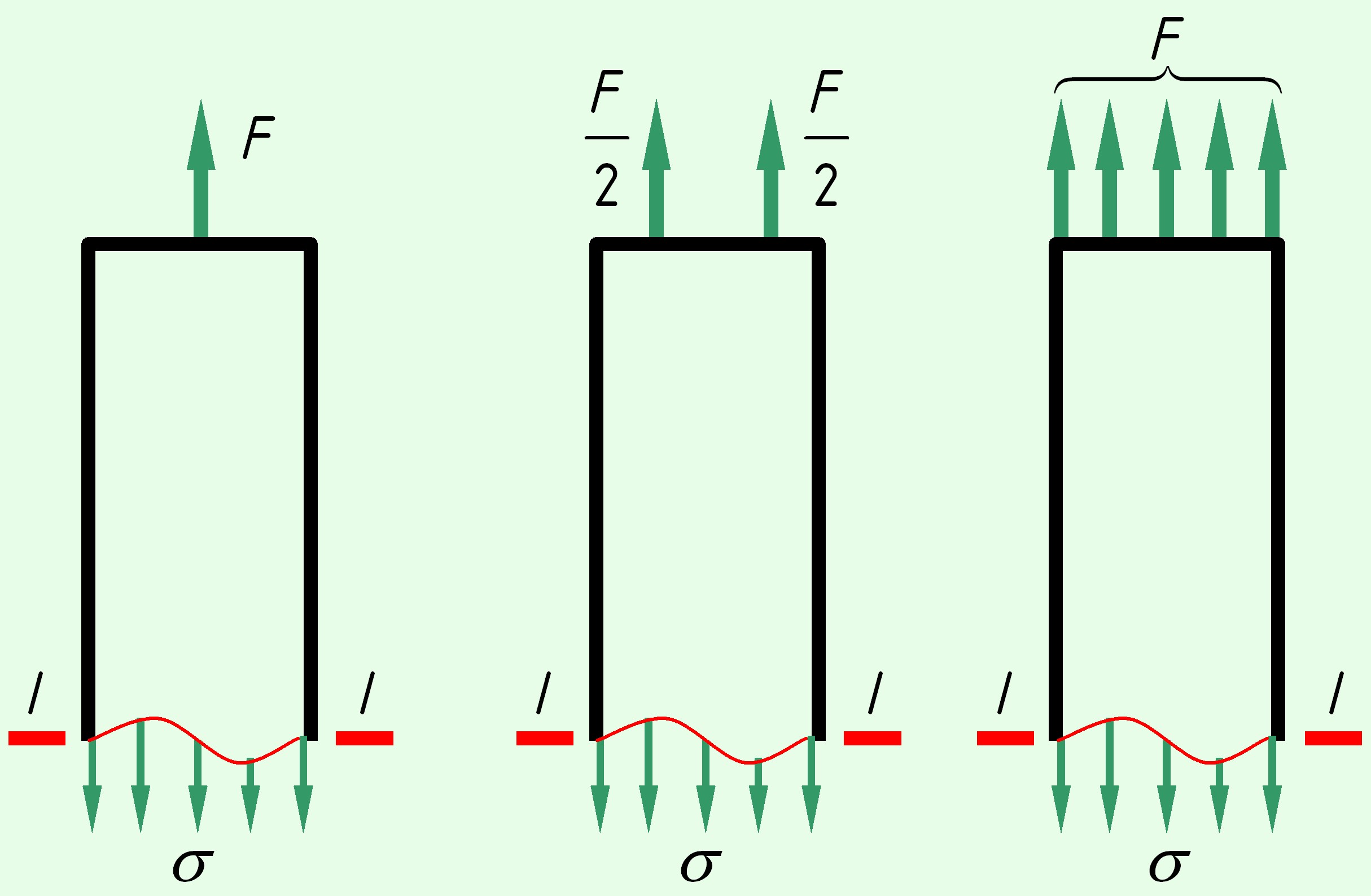
Рассмотрим идеально упругий призматический стержень прямоугольного поперечного сечения (рис. 1.2, а).
Выделим внутри стержня какие-либо две частицы K и L, расположенные на бесконечно малом расстоянии друг от друга. Для большей наглядности предположим, что между этими частицами имеется некоторая пружинка, удерживающая их на определенном расстоянии друг от друга. Пусть натяжение пружинки равно нулю.
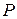
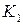
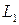
- Этапы метода сечений
- Внутренние силы в методе сечений
- Вычисление продольной и поперечных сил, крутящего и изгибающих моментов
- Продольная сила. Метод сечений. Эпюры продольных сил
- Внутренние силы при растяжении-сжатии
- Пример определения внутренних сил.
- Напряжения. Действующие и допускаемые напряжения
- $sigma = frac$
- Абсолютная и относительная деформация
- Продольная сила — внутренний силовой фактор
- Что такое продольная сила?
- Зачем нужна?
- Как определяется?
- Как обозначается?
- В чём измеряется?
- ТЕСТЫ ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ
- 💥 Видео
Видео:Сопротивление материалов. Лекция: метод сеченийСкачать

Этапы метода сечений
Метод сечений состоит из четырех последовательных этапов: разрезать, отбросить, заменить, уравновесить .
Разрежем стержень, находящийся в равновесии под действием некоторой системы сил 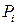
Отбросим одну из частей стержня и рассмотрим оставленную часть.
Поскольку мы как бы разрезали бесчисленное множество пружинок, соединявших бесконечно близкие частицы тела, разделенного теперь на две части, в каждой точке поперечного сечения стержня необходимо приложить силы упругости, которые при деформации тела возникли между этими частицами. Иными словами, заменим действие отброшенной части внутренними силами (рис. 1.3, б).
Видео:Тех.Мех. - это просто. 1 Метод сеченийСкачать

Внутренние силы в методе сечений
Разложим главный вектор и главный момент на составляющие по осям x, y (главные центральные оси) и z.
Получим 6 внутренних силовых факторов , возникающих в поперечном сечении стержня при его деформировании: три силы 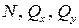
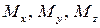
Сила N — продольная сила
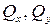
момент относительно оси z (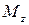
моменты относительно осей x, y (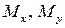
Запишем для оставленной части тела уравнения равновесия ( уравновесим ):
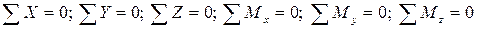
Из уравнений определяются внутренние усилия, возникающие в рассматриваемом поперечном сечении стержня.
Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Вычисление продольной и поперечных сил, крутящего и изгибающих моментов
продольная сила N равна сумме проекций всех сил (активных и реактивных), действующих на любую из частей рассеченного стержня, на ось z;
поперечные силы 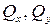
крутящий момент 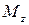
изгибающие моменты 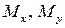
Видео:Внутренние силы. Определение. Метод сечений. Сопромат - Тайные Знания 6.Скачать
Продольная сила. Метод сечений. Эпюры продольных сил
Видео:Основы Сопромата. Внутренние силы. Эпюры внутренних усилий для пространственного стержняСкачать

Внутренние силы при растяжении-сжатии
Центральное растяжение-сжатие возникает в случае, когда на концах стержня вдоль его оси действуют две равные противоположно направленные силы. При этом в каждом сечении по длине стержня возникает внутреннее усилие ( продольная сила $N$ кН), которая численно равна сумме всех сил, которые действуют вдоль оси стержня и расположены с одной стороны от сечения.
Из условий равновесия отсеченной части стержня $N = F$.
Продольная сила при растяжении считается положительной, при сжатии – отрицательной .
Пример определения внутренних сил.
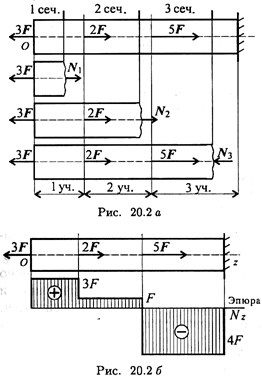
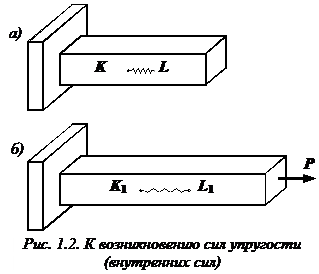
Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплен в стене (закрепление «заделка») (рис. 20.2а). Делим брус на участки нагружения.
Участком нагружения считают часть бруса между внешними силами.
На представленном рисунке 3 участка нагружения.
Воспользуемся методом сечений и определим внутренние силовые факторы внутри каждого участка.
Расчет начинаем со свободного конца бруса, чтобы не определять величины реакций в опорах.
Продольная сила положительна, участок 1 растянут.
Продольная сила положительна, участок 2 растянут.
Продольная сила отрицательна, участок 3 сжат.
Полученное значение N3 равно реакции в заделке.
Под схемой бруса строим эпюру продольной силы (рис. 20.2, б).
Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса.
Ось эпюры параллельна продольной оси.
Нулевая линия проводится тонкой линией. Значения сил откладывают от оси, положительные — вверх, отрицательные — вниз.
В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz.
Напряжения. Действующие и допускаемые напряжения
Величина внутренней силы дает представление о сопротивлении поперечного сечения в целом (интегрально), но не дает представления об интенсивности работы материала в отдельных точках сечения. Так, при равной продольной силе материал в стержне с большим сечением будет работать менее интенсивно, менее напряженно чем меньший.
Напряжения – внутренние силы, приходящиеся на единицу площади сечения. Напряжения, направленные перпендикулярно (по нормали) к сечению называются нормальными .
Видео:Ядро сеченияСкачать

$sigma = frac$
Единицы измерения напряжений — Па, кПа, МПа.
Знаки напряжений принимают так, как и для продольной силы.
Действующие напряжения — напряжения, которые возникают в рассматриваемом сечении.
Любой стержень в момент разрушения имеет определенные напряжения, которые зависят только от материала стержня и не зависят от площади сечения.
Допускаемые напряжения $left[ sigma right]$ – такие напряжения, которые не должны быть превышены в запроектированных конструкциях. Допустимые напряжения зависят от прочности материала, характера его разрушения, степени ответственности конструкции.
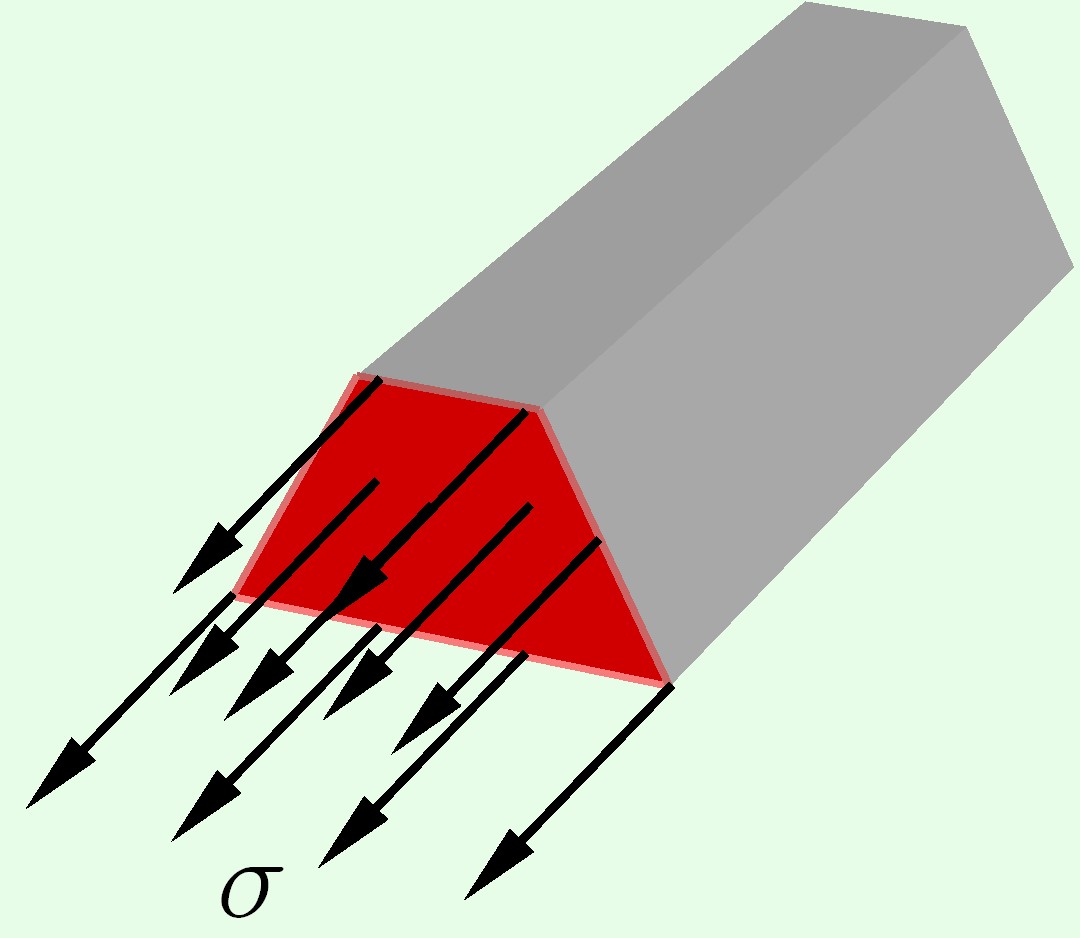
Принцип Сен-Венана : в сечениях, достаточно удаленных от места приложения нагрузки, распределение напряжений не зависит от способа приложения нагрузки, а зависит только от его равнодействующей.
то есть, распределение напряжений в сечении I-I для трех различных случаев, показанных на рисунке, принимается одинаковым.
Рисунок — иллюстрация принципа Сен-Венана
Видео:Решение системы уравнений методом Крамера 2x2Скачать

Абсолютная и относительная деформация
При растяжении возникает удлинение стержня – разница между длиной стержня до и после погрузки. Эта величина называется абсолютной деформацией .
Относительная деформация – отношение абсолютной деформации к первоначальной длине.
$sigma = E cdot varepsilon $
Таблица — физико-механические характеристики материалов
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Продольная сила — внутренний силовой фактор
В этой статье поговорим о таком внутреннем силовом факторе как продольная сила. Также дам ссылки на смежные статьи, которые каким-то образом связаны с продольной силой.
Видео:Определение усилий, напряжений и перемещений. СопроматСкачать

Что такое продольная сила?
Продольная сила – это внутренний силовой фактор, который возникает в поперечных сечениях элементов конструкций, работающих на растяжение (сжатие).
Конечно, продольная сила может появляться не только в элементах конструкций, которые работают только на чистое растяжение или сжатие. Она может возникать в сечениях, как ОДИН ИЗ силовых факторов, совместно с поперечной силой или изгибающим моментом при сложном сопротивлении.
Видео:Понимание напряжений в балкахСкачать

Зачем нужна?
Этот силовой фактор используется в расчётах на прочность и жёсткость элементов конструкций, работающих на растяжение (сжатие).
Зная значение продольной силы в поперечном сечении элемента конструкции, можно определить нормальное напряжение в этом сечении. А зная значение максимального нормального напряжния, которое, как правило, устанавливается из эпюры продольных усилий, осуществляются прочностные расчёты.
Видео:Введение в СопроматСкачать

Как определяется?
Как и другие внутренние силовые факторы, продольная сила определяется методом сечений.
Для того чтобы определить продольную силу в произвольном сечении элемента, его мысленно рассекают в этом сечении на две части, рассматриваются равновесие одной из частей, заменив действие отброшенной части продольной силой. Из уравнения статики, в частности, суммы проекций на одну из осей, выражается продольное усилие. Для построения эпюр эту процедуру проводят несколько раз, для каждого участка стержня (бруса).
Видео:Сопромат. Устойчивость. Продольный изгиб. Подбор сечения.Скачать

Как обозначается?
Продольная сила обозначается буквой N с индексом, который совпадает с названием продольной оси, направленной в сторону растяжения или сжатия нагруженного элемента и перпендикулярной поперечным сечениям.
Чаще всего, эта ось обозначается буквой – x. Например, таким образом: Nx
Видео:Сопромат. Часть 1. Растяжение (сжатие). Построение эпюр продольных сил и нормальных напряжений.Скачать

В чём измеряется?
Продольная сила, как и обычные внешние сосредоточенные силы, измеряется в ньютонах.
На практике, в расчётах используются килоньютоны (кН). Также иногда в литературе можно встретить размерность – кгс и тс.
Видео:Определение перемещений в балке. Метод сил. Правило Верещагина. СопроматСкачать

ТЕСТЫ ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ
1 ТЕСТЫ ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ ОСНОВНЫЕ ПОЛОЖЕНИЯ, МЕТОД СЕЧЕНИЙ, НАПРЯЖЕНИЯ Вариант Прямой брус нагружается внешней силой F. После снятия нагрузки его форма и размеры полностью восстанавливаются. Какие деформации имели место в данном случае? 1) незначительные, ) пластические, 3) упругие, 4) остаточные.. Как называют способность конструкции сопротивляться упругим деформациям? 1) пластичность, ) упругость, 3) устойчивость, 4) выносливость. 3. По какому из уравнений, пользуясь методом сечений, можно определить продольную силу в сечении? 1) Q x Fkx, ) Q y Fky, 3) N Fkz, 4) T М к М z Fk. 4. Пользуясь методом сечений определить величину поперечной силы в сечении I-I. 1) кн, ) 4 кн, 3) -6 кн, 4) 7 кн. 5. Какие напряжения возникают в поперечном сечении I-I бруса под действием крутящего момента М к?
2 1), ), 3),, 4) T М к — нормальное напряжение, — касательное напряжение.. Вариант Прямой брус нагружен силой F. Какую деформацию получил брус, если после снятия нагрузки форма бруса восстановилась до исходного состояния? 1) незначительную, ) пластическую, 3) остаточную, 4) упругую.. В каком случае материал считается однородным? А. Свойства материала не зависят от размеров. Б. Материал заполняет весь объём. В. Физико механические свойства материала одинаковы во всех точках. Г. Температура материала одинакова во всём объёме. 1) А, ) Б, 3) В, 4) Г. 3. Установить вид нагружения в сечении I-I
3 1) брус сжат, ) брус растянут, 3) брус закручен, 4) брус изогнут. 4. На брус действуют пары сил в плоскости уох. Определить величину внутреннего силового фактора в сечении I-I. 1) 40 кн м, ) 45 кн м, 3) 105 кн м, 4) 165 кн м. 5. Какие внутренние силовые факторы вызывают возникновение нормальных напряжений в сечении бруса? 1) N, ) М к Т, 3) Q y, 4) Q x. Вариант Как называется способность конструкции сопротивляться усилиям, стремящимся вывести её из исходного состояния равновесия? 1) прочность, ) жёсткость, 3) устойчивость, 4) выносливость.. Представлена диаграмма растяжения материала. Указать участок пластических деформаций. F, Н А В С D E о l, мм 1) ОА, ) ВЕ, 3) СD, 4) DE. К 3
4 3. Какое из уравнений равновесия нужно использовать для определения внутренних силовых факторов в сечении I-I методом сечений? 1) N z Fkz, ) Q y Fky, 3) M y M y Fk, 4) Т М z М z Fk. 4. Определить величину внутреннего силового фактора при указанном нагружении бруса в сечении I-I 1) 35 кн, ) 45 кн, 3) 5 кн, 4) 11 кн. 5. Как обозначаются касательные механические напряжения? 1), ) р, 3), 4). Вариант Прямой брус нагружен силой F (рис.1), после снятия нагрузки форма бруса изменилась (рис.). Какого типа деформацию получил брус? 4
5 Здесь, — прогиб под нагрузкой r — прогиб после снятия нагрузки (остаточный). 1) упругую, ) пластическую, 3) упругую и пластическую (остаточную), 4) незначительную.. Выбрать из приведенных ниже графиков график статической нагрузки. 1) А, ) Б, 3) В, 4) Г. 3. Какое из уравнений нужно использовать для определения внутреннего силового фактора в сечении I-I методом сечений? Моменты действуют в плоскости уох. 1) Fkz 3) y Fky T M z M z Fk, M y M y Fk. N, ) Q, 4) 4. Определить величину внутреннего силового фактора при указанном нагружении бруса в сечении I-I. 1) 36 кн, ) 3 кн, 3) -8 кн, 4) 18 кн. 5
6 5. В каких единицах измеряется механическое напряжение в системе единиц СИ? 1) кгс/см, ) Н мм, 3) кн/мм, 4) Па. Вариант Как называется способность конструкции сопротивляться упругим деформациям? 1) упругость, ) пластичность, 3) устойчивость, 4) износостойкость.. Представлена диаграмма растяжения материала. Назвать участок, где деформации только упругие 1) ОА, ) АВ, 3) ВD, 4) CD. 3. Какой внутренний силовой фактор возникает в поперечном сечении бруса при растяжении? 1) Q x, ) Q у, 3) N, 4) Т М к. 4. Пользуясь методом сечений, найти поперечной силы в сечении I-I. 1) 0 кн, ) 36 кн, 3) 40 кн, 4) 48 кн. 5. Какие механические напряжения в поперечном сечении бруса при нагружении называют нормальными? 6
7 1) возникающие при нормальной работе, ) направленные перпендикулярно площадке, 3) направленные параллельно площадке, 4) направленные наклонно к площадке.. ОСНОВНЫЕ МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ Вариант.1 1. Как называется и обозначается напряжение, при котором деформации растут при постоянной нагрузке? 1) предел прочности u, ) предел текучести y, 3) допускаемое напряжение adm, 4) предел пропорциональности pr.. Определить допускаемое напряжение, если F pr = 1,6 кн, F y = кн, F u = 5,0 кн, коэффициент запаса n y, площадь поперечного сечения А = 40 мм. 1) 5 МПа, ) 0 МПа, 3) 50 МПа, 4) 6,5 МПа. 3. Вычислить максимальное удлинение в момент разрыва, если начальная длина образца 00 мм, а длина в момент разрыва 40 мм. 1) 0%, ) 17%, 3) 0,5%, 4) 1%. 4. Выбрать основные характеристики прочности материала. 1) u, y, ) y, pr, 3) pr, y, 4) r r. 5. Проверить прочность материала, если максимальное напряжение в сечении =40 МПа, pr = 380 МПа, y = 400 МПа, u = 640 МПа, коэффициент запаса n y 1, 5. 1) adm, ) adm, 3) adm, 4) данных недостаточно. 7
8 Вариант. 1. В какой точке диаграммы растяжения на образце образуется шейка? 1), ) 1, 3) 3, 4) 4.. До какого из приведенных напряжений в материале выполняется зависимость E? 1) до pr, ) до e, 3) до y, 4) до u. 3. Выбрать точную запись условия прочности при растяжении и сжатии. N A N A N A 1) adm, ) adm, 3) adm, 4) adm. 4. Найти допускаемое напряжение для материала, если получены следующие данные: F pr = 60 кн, F y = 6,5 кн, F u = 100 кн; коэффициент запаса n y, 5; площадь поперечного сечения образца 00 мм. 1) 50 МПа, ) 15 МПа, 3) 00 МПа, 4) 300 МПа. 5. Проверить прочность материала, если максимальное напряжение в сечении 400 МПа, pr = 40 МПа, y = 500 МПа, u = 60 МПа, коэффициент запаса n y 1, 5. 1) adm, ) adm, 3) adm, 4) данных недостаточно. N A 8
9 Вариант.3 1. Используя приведенную диаграмму растяжения, указать остаточную деформацию образца для точки К. 1) ОМ, ) OL, 3) MN, 4) ME.. Как называется и обозначается наибольшее напряжение, до которого выполняется закон Гука? 1) u — предел прочности, ) y — предел текучести, 3) e — предел упругости, 4) pr — предел пропорциональности. 3. Какое напряжение считают предельным для пластичного материала? 1) e, ) pr, 3) u, 4) y. 4. Первоначальная длина образца 400 мм, длина образца при разрушении 500 мм. Определить максимальное удлинение при разрыве. 1) 0,33, ) 100 мм, 3) 33%, 4) 5%. 5. Проверить прочность материала, если максимальное рабочее напряжение =500 МПа, pr = 70 МПа, u = 980 МПа, коэффициент запаса n u. 1) adm, ) adm, 3) adm, 4) данных недостаточно. Вариант.4 1. Выбрать на диаграмме растяжения участок общей текучести материала. 9
10 1) 01, ) 1, 3) 4, 4) 3.. Как обозначается характеристика, определяющая допускаемое напряжение для хрупких материалов? 1) pr, ) y, 3) e, 4) u. 3. Выбрать точную запись условия прочности при растяжении и сжатии N A N A N A N A 1) adm, ) adm, 3) adm, 4) adm. 4. Найти предел текучести материала, если F pr = 4 кн, F y = 8 кн, F u = 40кН, площадь поперечного сечения образца 50 мм. 1) 80 МПа, ) 470 МПа, 3) 560 МПа, 4) 60 МПа. 5. Проверить прочность материала, если максимальное напряжение =40 МПа, pr = 380 МПа, y = 400 МПа, u = 640 МПа, коэффициент запаса по пределу прочности n u, 5., ) adm, 3) adm, 4) данных недостаточно. 1) adm Вариант.5 1. Указать точку на диаграмме растяжения, до которой в материале возникают упругие деформации. 10
11 1) точка 1, ) точка, 3) точка 3, 4) точка 4.. При каком из перечисленных напряжений образец разрушается? 1) e, ) pr, 3) u, 4) y. 3. Выбрать основные характеристики пластичности материала. 1) y, pr ; ) r, r ; 3) pr, u ; 4) u, y. 4. Найти допускаемое напряжение материала, если pr = 30 МПа, y = 350 МПа, n u. u = 60 МПа, коэффициент запаса по пределу прочности 1) 100 МПа, ) 140 МПа, 3) 310 МПа, 4) 5 МПа. 5. Определить предел прочности материала, если F pr = 4800 Н, F y = 500 Н, А = 40 мм. F u = 800 Н, площадь поперечного сечения образца 1) 15 МПа, ) 150 МПа, 3) 175 МПа, 4) 05 МПа. 11
12 3. РАСЧЁТЫ НА ПРОЧНОСТЬ ПРИ РАСТЯЖЕНИИ И СЖАТИИ Вариант Выбрать соответствующую эпюру продольных сил для бруса. A 1 =1000 мм A B C C 38 кн C кн 54 кн A =500 мм Эп. N Эп. N Эп. N 1) А, ) В, 3) С, 4) соответствующей эпюры не представлено.. Для бруса из вопроса 1 определить наибольшую продольную силу, возникшую в поперечном сечении. 1) -16 кн, ) -38 кн, 3) 70 кн, 4) -54 кн. 3. Найти нормальное напряжение в сечении С-С бруса из вопроса 1. 1) -38 МПа, ) — МПа, 3) 16 МПа, 4) 1 МПа. 4. Чему равен коэффициент запаса прочности в сечении С-С бруса? Механические характеристики материала y = 0 МПа, u = 400 МПа. Использовать результаты, полученные при ответе на вопрос 3. 1) 18, ) 10, 3) 4,, 4) 7,4. 5. Определить удлинение стержня АВ. Стальной стержень длиной 3 м нагружен силой 40 кн, поперечное сечение стержня швеллер 10, модуль упругости материала 10 5 МПа 1) 3,5 мм, ) 3,3 мм, 3) мм, 4) мм. 1
13 Вариант Выбрать соответствующую эпюру продольных сил для бруса. 1) А, ) Б, 3) В, 4) Г.. Для бруса из вопроса 1 определить наибольшую продольную силу, возникшую в поперечном сечении. 1) 306 кн, ) 70 кн, 3) 100 кн, 4) -30 кн. 3. Найти нормальное напряжение в сечении С-С бруса из вопроса 1. 1) 00 МПа, ) 100 МПа, 3) 70 МПа, 4) -60 МПа. 4. Обеспечена ли прочность бруса в сечении С-С (вопрос3), если известны механические характеристики материала: y = 560 МПа, u = 870МПа, а коэффициент запаса по пределу текучести n y. 1) adm, ) adm, 3) adm, 4) данных недостаточно. 5. Однородный жёсткий брус весом G = 0 кн нагружен силой F = 10 кн. Длина стержня АВ = 4 м; материал сталь E = 10 5 МПа, поперечное сечение двутавр 10. Определить удлинение стержня АВ. 13
14 1) 0,7 мм, ) 0,4 мм, 3) 0, мм, 4) 0,615 мм. Вариант Выбрать соответствующую эпюру продольных сил для бруса. A =1000 мм A Б B Г 85 кн + C 35 кн C ) А, ) Б, 3) В, 4) Г. 50 кн =500 мм A 1 Эп. N Эп. N Эп. N Эп. N. Для бруса из вопроса 1 определить наибольшую продольную силу, возникшую в поперечном сечении. 1) 190 кн, ) 50 кн, 3) — 85 кн, 4) 35 кн. 3. Найти нормальное напряжение в сечении С-С бруса из вопроса 1. 1) 70 МПа, ) 0, 3) -85 МПа, 4) -50 МПа. 4. Чему равен коэффициент запаса по сравнению с пределом текучести в сечении С-С бруса, если механические характеристики материала 14
15 y = 80 МПа, ответе на вопрос 3. u = 560 МПа. Использовать результаты, полученные при 1) 3,3; ) 6,6; 3) 4; 4) Стальной стержень длиной 4 м нагружен силой F = 360 кн, поперечное сечение стержня швеллер 8, модуль упругости материала E = 10 5 МПа. Определить удлинение стержня АВ. 1) среди данных ответов верного нет; ) 0,007 мм; 3) 0, мм; 4) 8 мм. Вариант Выбрать соответствующую эпюру продольных сил для бруса. 1) А, ) Б, 3) В, 4) Г.. Для бруса из вопроса 1 определить наибольшую продольную силу, возникшую в поперечном сечении. 1) 0 кн, ) 90 кн, 3) 50 кн, 4) 70кН. 3. Определить нормальное напряжение в сечении С-С бруса из вопроса 1. 1) 100 МПа, ) 90 МПа, 3) 70 МПа, 4) 50 МПа. 15
16 4. Обеспечена ли прочность бруса в сечении С-С (вопрос 3), если известны механические характеристики материала y = 80 МПа, = 560 МПа, коэффициент запаса n 4. Схема бруса на рисунке к во- u просу 1. y, ) adm, 3) adm, 4) данных недостаточно. 1) adm 5. Однородный жёсткий брус весом G = 4 кн нагружен силой F = кн. Длина стержня АВ = 6 м, материал сталь E = 10 5 МПа, поперечное сечение бруса швеллер 6,5. Определить удлинение стержня АВ. G A B м 1 м м 1) 0,03 мм, ) 0,0 мм, 3) 0,1 мм, 4) 0,18 мм. Вариант Выбрать соответствующую эпюру продольных сил для бруса. F 1) А, ) Б, 3) В, 4) Г. 16
17 . Для бруса из вопроса 1 определить наибольшую продольную силу, возникшую в поперечном сечении. 1) 30 кн, ) 40 кн, 3) 70 кн, 4) 100кН. 3. Определить нормальное напряжение в сечении С-С бруса из вопроса 1. 1) 100 МПа, ) 140 МПа, 3) 80 МПа, 4) 60 МПа. 4. Обеспечена ли прочность бруса в сечении С-С (вопрос 3), если известны механические характеристики материала y = 540 МПа, u = 800 МПа, коэффициент запаса по пределу текучести n y 1, 5. Схема бруса на рисунке к вопросу 1. 1) adm, ) adm, 3) adm, 4) для ответа данных недостаточно. 5. Однородный жёсткий брус весом G = 10 кн нагружен силой F = 8 кн. Длина стержня АВ равна 3 м, материал сталь E = 10 5 МПа, поперечное сечение двутавр 10. Определить удлинение стержня АВ. 1) 0,03 мм, ) 0,084 мм, 3) 0,15 мм, 4) 0,84 мм. 4. ПРАКТИЧЕСКИЕ РАСЧЁТЫ НА СРЕЗ И СМЯТИЕ Вариант Листы соединены болтом, поставленным без зазора. Соединение нагружено растягивающей силой F=50,4 кн, определить величину одной площадки среза болта, если d c = 1мм; l = 45 мм, =0 мм. 17
18 1) 69 мм, ) 346 мм, 3) 66 мм, 4) 40 мм.. Выбрать формулу для определения напряжений сдвига в поперечном сечении болта (рисунок к вопросу 1). 1) N A, ) Q A T Q A, 3), 4). W p 3. Найти площадь смятия внутреннего листа соединения (рисунок к вопросу 1), нагруженного растягивающей силой 1) 346 мм, ) 40 мм, 3) 55 мм, 4) 840 мм. 4. Проверить прочность внутреннего листа соединения (рисунок к вопросу 1) на смятие, если допускаемое напряжение смятия материала листа 10 МПа. Остальные данные для расчёта в задании 1. 1) см adm, см, ) см adm, см, 3) см adm, см, 4) для ответа данных недостаточно. 5. Из условия прочности заклёпок на срез определить допускаемую нагрузку на соединение, если d = 16 мм, 1 = 18 мм, = 0 мм, adm,ср = 100 МПа, adm, см = 40 МПа. 18
19 1) 0,1 кн; ) 40, кн; 3) 8,8 кн; 4) 61,1 кн. Вариант Стержни I и II соединены штифтом III и нагружены растягивающими силами. Найти суммарную площадь среза штифта. 16 F F I 1) 100,5 мм, ) 40 мм, 3) 01 мм, 4) 51 мм. III II. Выбрать формулу для определения напряжений в поперечном сечении детали при сдвиге. 1) N A, ) Q A, 3) T, 4) W p M x. Wx 3. Определить площадь смятия штифта, изображённого на рисунке к вопросу 1. 1) 64 мм, ) 18 мм, 3) 01 мм, 4) 317 мм. 19
20 4.Из условия прочности на срез определить допускаемую нагрузку для штифта (рис. к вопросу 1). Материал детали сталь, допускаемое напряжение adm, ср = 80 МПа. 1) 16 кн, ) 3,7 кн, 3) 3 кн, 4) 8 кн. 5. Из расчёта на смятие определить количество заклёпок, необходимое для передачи внешней силы F = 10 кн, если adm, ср = 80 МПа, adm,см = 40 МПа, d = 0 мм. 1), ) 3, 3) 4, 4) 7. Вариант Стержни I и II соединены штифтом III и нагружены растягивающими силами. Рассчитать величину суммарной площади среза штифта. 0 F F I III II 1) 800 мм, ) 68 мм, 3) 960 мм, 4) 156 мм.. Выбрать формулу для расчёта напряжения в поперечном сечении детали при сдвиге. 1) G, ) Q A, 3) N A T, 4). W p 0
21 3. Рассчитать величину площади смятия штифта, изображённого на рисунке к вопросу 1. 1) 400 мм, ) 51, мм, 3) 160 мм, 4) 800 мм. 4. Из условия прочности на срез определить допускаемую нагрузку для штифта (рис. к вопросу 1). Материал детали сталь, допускаемое напряжение adm, ср = 100 МПа. 1) 800 кн, ) 94,8 кн, 3) 6,8 кн, 4) 110,5 кн. 5. Из расчёта на смятие определить количество заклёпок, необходимое для передачи внешней силы F = 180 кн, если adm, ср = 80 МПа, adm,см = 40 МПа, d = 16 мм. 1) 3, ) 4, 3) 5, 4) 6. Вариант Шпилька d = 16 мм удерживает стальной лист 1 ( = 10 мм, ширина листа b = 80 мм). Найти площадь среза шпильки под действием силы F. 1
22 1) 40 мм, ) 01 мм, 3) 160 мм, 4) 30 мм.. Выбрать формулу для расчёта шпильки на срез (рис. к вопросу 1). M 1) x Q adm, ) adm, Wx A T F 3) adm, 4) см adm, см. W p A 3. Определить площадь смятия стального листа под действием растягивающей силы. Данные для расчёта взять из задания 1 (рис. к вопросу 1). 1) 01 мм, ) 160 мм, 3) 44 мм, 4) 30 мм. 4. Проверить прочность стального листа I на смятие (данные для расчёта в вопросе 1), если F = 6 кн, adm, ср = 100 МПа, adm,см = 40 МПа. 1) см adm, см, ) см adm, см, 3) см adm, см, 4) для ответа данных недостаточно. 5. Из расчёта на срез заклёпочного соединения определить необходимое количество заклёпок если F = 363 кн, 1 = 10 мм, = 0 мм, adm,ср = 100 МПа, adm, см= 40 МПа, d = 17 мм. 1) 4, ) 5, 3) 6, 4) 8.
23 Вариант Болт нагружен растягивающей силой. Определить величину площади среза головки болта под действием силы F. H = 5 мм, h = 10 мм, d = 1 мм, D = 0 мм. H h 1) 188 мм, ) 376 мм, 3) 314 мм, 4) 94 мм.. Выбрать формулу для расчёта головки болта на срез под действием внешней силы F (рис. к вопросу 1). N A Q A T 1), ), 3), 4) W см p A. 3. Стальные листы соединены штифтом I. Определить минимальную величину площади смятия листа при воздействии внешней силы F, если 1= 0 мм, = 5 мм, d = 7 мм. F 1) 540 мм, ) 57 мм, 3) 675 мм, 4) 1695 мм. 4. Из условия прочности листа на смятие (рис. к вопросу 3) определить допускаемую нагрузку, если adm, ср = 100 МПа; adm, см= 40 МПа. 1) 19,6 кн, ) 54 кн, 3) 57, кн, 4) 16 кн. 3
24 5. Из расчёта на срез заклёпочного соединения найти необходимое количество заклёпок, если F = 50 кн, d = 13 мм, 1 = 1 мм, = 40 мм, adm,ср = 100 МПа, adm, см= 40 МПа. 1), ) 3, 3) 4, 4) ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ Вариант В каком случае значение I x минимально? 1) А, ) Б, 3) В, 4) Г.. Вычислить I y — момент инерции сечения относительно оси у
25 1) мм 4, ) мм 4, 3) мм 4, 4) мм Определить полярный момент инерции кольца, если осевой момент инерции равен I x = 6 см 4. 1) 3 см 4, ) 6 см 4, 3) 1 см 4, 4) 18 см Определить координату x c центра тяжести равнополочного уголка. 1) 60 мм; ) 198 мм; 3) 158, мм; 4) 10, мм. 5. Найти осевой момент инерции двутавра относительно оси, проходящей через основание. 1) 350 см 4 ; ) 879, см 4 ; 3) 438, см 4 ; 4) 1317, см 4. Вариант В каком случае значение I у максимально? 5
26 ) А, ) Б, 3) В, 4) Г.. Выбрать формулу определения главного центрального момента инерции сечения относительно оси х d bh d bh d bh d bh 1), ), 3), 4) Найти полярный момент инерции кольца, если осевой момент инерции равен I x = 14 см 4. 1) 7 см 4, ) 36 см 4, 3) 14 см 4, 4) 8 см Определить координату y c центра тяжести швеллера. 6
27 1) 54 мм; ) 114,4 м; 3) 68,4 мм; 4) 94 мм. 5. Вычислить осевой момент инерции швеллера относительно оси, проходящей через основание. 1) 113 см 4 ; ) 1419 см 4 ; 3) 160,3 см 4 ; 4) 13,3 см 4. Вариант Выбрать формулу для определения осевого момента инерции сечения относительно его главной центральной оси у. H h 1) 3 4 Bh d, ) HB d d BH, 3), 4) hb d Найти осевой момент инерции I x. 1) мм 4, ) мм 4, 3) мм 4, 4) мм 4. 7
28 3. Определить полярный момент инерции сечения, если осевой момент инерции I y = 15,5 см 4. 1) 11,6 см 4 ; ) 31 см 4 ; 3) 15,5 см 4 ; 4) 45,5 см Вычислить координату y c двутавра. 1) 150, ) 110, 3) 180, 4) Найти осевой момент инерции равнополочного уголка относительно оси x 1. 1) 5,53 см 4 ; ) 10,73 см 4 ; 3) 16, см 4 ; 4) 3,38 см 4. Вариант Диаметр сплошного вала увеличен в 3 раза. Во сколько раз увеличились главные центральные моменты инерции? 1) в 6 раз, ) в 81 раз, 3) в 3 раза, 4) в 9 раз. x 1 8
29 . Выбрать вариант, для которого главный центральный момент инерции сечения относительно оси х можно найти по формуле 3 3 BH bh Ix. 1 1 h H h H h H 1) А, ) В, 3) Б, 4) верный ответ не приведён. 3. Найти главный центральный момент инерции сечения I x, если полярный момент инерции равен 48 см 4. B 1) 496 см 4, ) 348 см 4, 3) 48 см 4, 4) 14 см Определить координату y c центра тяжести швеллера. 1) 78 мм; ) 93,4 мм; 3) 135,4 мм; 4) 104,6 мм. 5. Вычислить осевой момент инерции двутавра относительно оси х 1. 9
30 1) 785 см 4, ) 1170 см 4, 3) 49 см 4, 4) 1840 см 4. Вариант Диаметр сплошного вала уменьшен в 4 раза. Во сколько раз изменится полярный момент инерции вала? 1) уменьшится в 4 раза, ) увеличится в 4 раза, 3) уменьшится в 64 раза, 4) уменьшится в 56 раз.. Выбрать формулу для вычисления главного центрального момента инерции сечения относительно оси х. 1) 4 3 H bh, ) H bh H hb a A, 3), 4) H bh Определить величину полярного момента инерции сечения, если главные центральные моменты инерции соответственно равны I x = 7 см 4 ; I y = 3,5 см 4. 1) 7 см 4, ) 3,5 см 4, 3) 10,5 см 4, 4) 4,5 см Найти координату yc центра тяжести швеллера. y с 14 о x 30
31 1) 4 мм, ) 58,7 мм, 3) 83,3 мм, 4) 141,3 мм. 5. Вычислить осевой момент инерции швеллера относительно оси х (рис. к вопросу 4). 1) 491 см 4, ) 537,6 см 4, 3) 583 см 4, 4) 108 см КРУЧЕНИЕ 1 Вариант Как выглядит образец после испытания на кручение? 1) искривлен и разрушен, ) растянут и разрушен, 3) перерезан перпендикулярно продольной оси, 4) разрушен под углом 45 к оси.. Какое из напряжённых состояний называют чистым сдвигом? 1) А, ) Б, 3) В, 4) Г. 3. Как называется указанная величина в законе Гука? G 1) угол закручивания, ) смещение, 3) сжатие, 4) угол сдвига. 4. Выбрать формулу для определения напряжения в указанной точке поперечного сечения. 31
32 1) T, ) W p I p T, 3) G, 4) Q A. 5. Определить максимальное напряжение в сечении бруса. Диаметр бруса 50 мм, крутящий момент в сечении 00 Н м. 1) 8,15 МПа, ) 16 МПа, 3) 4 МПа, 4) 3 МПа. Вариант Назвать деформацию при кручении. 1) смещение, ) угол сдвига, 3) угол закручивания, 4) сжатие.. Как изменится диаметр круглого вала после испытания на кручение. 1) увеличится, ) уменьшится, 3) искривится, 4) не изменится. 3. Выбрать верную запись закона Гука при сдвиге. 1) T, ) G, 3) I p Q A, 4) T. W p 4. Как изменится напряжение на поверхности круглого бруса, если крутящий момент увеличится в 3 раза? 1) увеличится в 3 раза, ) уменьшится в 3 раза, 3) увеличится в 9 раз, 4) не изменится. 3
33 5. Образец диаметром 5 мм разрушился при испытании на кручение при крутящем моменте 175 Н м. Определить максимальное напряжение в сечении образца. 1) 36 МПа, ) 57 МПа, 3) 76 МПа, 4) 8 МПа. Вариант Что происходит с поперечным сечением бруса при кручении (рисунок к вопросу 5)? 1) расширяется, ) сужается, 3) искривляется, 4) не изменяется.. Какие деформации возникают в каждом элементе бруса при кручении? 1) растяжение, ) сжатие, 3) сдвиг, 4) изгиб. 3. Назвать пропущенную величину в законе Гука при сдвиге. 1) модуль упругости, ) модуль сдвига, 3) коэффициент поперечной деформации, 4) момент сопротивления. 4. Выбрать формулу для расчёта напряжения точке А при кручении. 1) Q A, ) W p T, 3) G, 4) T. I p 5. Определить максимальное напряжение в сечении бруса. Диаметр бруса 35 мм, крутящий момент в сечении 1 Н м. 33
34 1) 8,67 МПа; ) 13,05 МПа; 3) 6,3 МПа; 4) 34,67 МПа. Вариант Выбрать напряжённое состояние, называемое чистым сдвигом. А Б В Г 1) А, ) Б, 3) В, 4) Г.. Указать единицы измерения величины, выделенной в представленной формуле G. 1) Н м, ) мм 3, 3) рад, 4) МПа. 3. Напряжение в точка А поперечного сечения круглого бруса равно 18 МПа, чему равно напряжение в точке B? 1) 4,5 МПа, ) 9 МПа, 3) 18 МПа, 4) 7 МПа. 4. Что происходит с поперечным сечением бруса при кручении? 1) расширяется, ) сужается, 3) искривляется, 4) поворачивается. 34
35 5. При испытании на кручение круглый брус разрушается при моменте 11 Н м. Диаметр бруса 0 мм. Определить разрушающее напряжение. 1) 36, МПа, ) 8 МПа, 3) 71,3 МПа, 4) 8 МПа. Вариант Какой буквой принято обозначать деформацию при кручении? 1), ) Δl, 3), 4).. Выбрать пропущенную величину в формуле, определяющей напряжение при кручении Т? 1), ) d, 3) l, 4) G. I p 3. Как распределяются напряжения в поперечном сечении вала при кручении? 1) А, ) Б, 3) В, 4) Г. 4. Как изменится максимальное напряжение в сечении при кручении, если диаметр вала уменьшится в раза? 1) уменьшится в раза, ) уменьшится в 8 раз, 3) увеличится в раза, 4) увеличится в 8 раз. 35
36 5. Образец диаметром 3 мм разрушился при крутящем моменте 18 Н м. Определить разрушающее напряжение. 1) 36,5 МПа; ) 4,5 МПа; 3) 19,9 МПа; 4) 15,55 МПа. 7. КРУЧЕНИЕ Вариант Какой из участков вала постоянного сечения наиболее опасен по прочности? 1) 1 участок, ) участок, 3) 3 участок, 4) 4 участок.. В каком порядке следует расположить шкивы (см. схему к вопросу 1), чтобы получить минимальную нагрузку на вал? 1) m 1, m, m 0, m 3 ; ) m 3, m 1, m 0, m ; 3) m 1, m, m 3, m 0 ; 4) m 3, m, m 0, m Выбрать формулу для определения угла закручивания вала. T 1) r, ) l, 3), 4) l. GI l p G 4. Найти диаметр вала из расчёта на прочность, если подаваемая мощность 15 квт, скорость вращения 50 рад/с, допускаемое напряжение 5 МПа. 1) 31 мм, ) 44 мм, 3) 54 мм, 4) 39 мм. 5. От каких факторов зависит выделенная величина? T I 1) от материала, ) от нагрузки, 3) от длины вала, 4) от диаметра. p 36
37 Вариант Выбрать эпюру крутящих моментов, соответствующую заданной схеме вала. 1) А, ) Б, 3) В, 4) верный ответ не приведен.. В каком порядке следует расположить шкивы (см. схему к вопросу 1), чтобы получить минимальную нагрузку на вал? 1) m 1, m, m 3, m 0 ; ) m 1, m 3, m 0, m ; 3) m, m 3, m 0, m 1 ; 4) m 3, m 0, m 1, m. 3. От каких факторов зависит выделенная в формуле величина? T max 1) от материала, ) от нагрузки, 3) от длины вала, 4) от диаметра. 4. Проверить прочность вала, если максимальный крутящий момент 80 Н м, диаметр вала 5 мм, допускаемое напряжение 40 МПа. 1) max adm, ) max adm, 3) max adm, 4) данных недостаточно. W p 37
38 5. Как изменится угол закручивания вала, если крутящий момент уменьшится в 8 раз, а диаметр вала уменьшится в раза? 1) увеличится в раза, ) уменьшится в 4 раза, 3) увеличится в 8 раз, 4) уменьшится в 16 раз. Вариант Какому нагружению вала соответствует данная эпюра? m 1 = 1 Н м, m = 8 Н м, m 3 = 60 Н м, m 4 = 18 Н м.. По эпюре из вопроса 1 определить максимальную внешнюю нагрузку на вал. 1) 118 Н м, ) 78 Н м, 3) 60 Н м, 4) 48 Н м. 3. Выбрать верную запись условия жесткости при кручении T T 1) adm, ) adm, GI p GI p T T 3) adm, 4) adm. GI p GI p 4. Определить диаметр вала по условию прочности, если вал передаёт мощность 6,8 квт, при скорости вращения 16 рад/с, а допускаемое напряжение 30 МПа. 1) 4, мм, ) 36 мм, 3) 4 мм, 4) 5, мм. 5. Как изменится максимальное напряжение при кручении, если крутящий момент увеличится в 4 раза, а диаметр вала увеличится вдвое? 38
39 1) уменьшится в раза, ) увеличится в раза, 3) уменьшится в 4 раза, 4) увеличится в 8 раз. Вариант Чему равен максимальный крутящий момент на валу? 1) Т = 300 Н м, ) Т = 1000 Н м, 3) Т = 500 Н м, 4) Т = 400 Н м.. В каком порядке рациональнее расположить шкивы на валу (см. схему к вопросу 1), чтобы получить минимальную нагрузку на вал? 1) m 1, m, m 0, m 3, m 4 ; ) m 1, m, m 3, m 0, m 4 ; 3) m 1, m 4, m 0, m, m 3 ; 4) m, m 3, m 4, m 0, m 1. 3 Указать единицы измерения величины, выделенной в формуле T. 1) МПа, ) мм, 3) мм 3, 4) мм Проверить прочность бруса, если максимальный крутящий момент 500 Н м, диаметр бруса 0 мм, допускаемое напряжение 5 МПа. 1) max adm, ) max adm, 3) max adm, 4) данных недостаточно. 5. Как изменится угол закручивания, если крутящий момент уменьшится в раза, а диаметр увеличится в 4 раза? 1) увеличится в 56 раз, ) увеличится в 18 раз, 3) уменьшится в 51 раз, 4) уменьшится в 56 раз. I p 39
40 Вариант Выбрать эпюру крутящих моментов, соответствующую данной схеме вала m 1 =18 Н м m =5 Н м m 0 m 3 =300 Н м 18 Т, Н м А Т, Н м Б ) А, ) Б, 3) В, 4) верный ответ не приведен. Т, Н м В. В каком порядке рациональнее расположить шкивы на валу (см. схему к вопросу 1), чтобы получить минимальную нагрузку на вал? 1) m 1, m, m 0, m 3 ; ) m 1, m, m 3, m 0 ; 3) m 3, m 1, m 0, m 3 ; 4) m 3, m, m 0, m Указать единицы измерения величины, выделенной в формуле T I. 1) МПа, ) мм, 3) мм 3, 4) Н м. 4. Определить необходимый диаметр бруса, если максимальный крутящий момент 500 Н м, а допускаемое напряжение материала adm = 50 МПа. 1) 37 мм; ) 4 мм; 3) 3,7 мм; 4) 70 мм. p 40
41 5. Как изменится угол закручивания, если крутящий момент и диаметр увеличатся в 4 раза? 1) увеличится в 4 раза, ) увеличится в 56 раз, 3) уменьшится в 56 раз, 4) уменьшится в 64 раза. 8. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ В БАЛКАХ ПРИ ИЗГИБЕ ОТ СОСРЕДОТОЧЕННЫХ НАГРУЗОК Вариант Выбрать участок чистого изгиба 1) 1 участок, ) участок, 3) 3 участок, 4) 4 участок.. Выбрать формулу для определения изгибающего момента в сечении ) F 1 z 3 М 1 + F (z 3 3) F 3, ) -F 1 z 3 М 1 — F (z 3 3) F 3 (z 3-6), 3) F 1 z 3 + М 1 + F (z 3 3) F 3, 4) -F 1 z 3 М 1 + F (z 3 3) F 3 (z 3-6). 3. Определить величину изгибающего момента в сечении Г слева (схема к вопросу ), если F 1 = 10 кн, F = 0 кн, F 3 = 8 кн, М 1 = 18 кн м, М = 36 кн м, М 3 = 5 кн м. 1) 54 кн м, ) 98 кн м, 3) 6 кн м, 4) 90 кн м. 41
42 4. Из представленных на схеме эпюр выбрать эпюру поперечной силы для изображённой балки. 0,5 0 0,5 0,5 кн 4 м 10 9,5 15 кн м 10 кн 9,5 4 м м м 1 1) А, ) Б, 3) В, 4) Г. 9,5 кн 40 0 кн 0 z А Б 0,5 0,5 0 0,5 кн 4 м 9,5 9, В 0 15 кн м 10 кн 9,5 кн 4 м м м кн 5. Из представленных в вопросе 4 эпюр выбрать эпюру изгибающих моментов для балки. 1) Б, ) В, 3) Д, 4) Е. Вариант Выбрать участок чистого изгиба 0 z Г Д Е 1) 1 участок, ) участок, 3) 3 участок, 4) 4 участок.. Выбрать формулу для определения изгибающего момента в сечении
43 1) F 1 z 3 М + F (z 3 3), ) -F 1 z 3 + М — F (z 3 6), 3) F 1 z 3 + М — F z 3, 4) F 1 z 3 М + F (z 3 6). 3. Определить величину изгибающего момента в сечении Г (схема к вопросу ), если F 1 = кн, F = 18 кн, F 3 = 36 кн, М = 36 кн м. 1) 138 кн м, ) 10 кн м, 3) 198 кн м, 4) 176 кн м. 4. Из представленных на схеме эпюр выбрать эпюру поперечной силы для изображённой балки. 1) Б, ) В, 3) Д, 4) Е. 5. Из представленных в вопросе 4 эпюр выбрать эпюру изгибающих моментов для балки. 1) А, ) Г, 3) Д, 4) Е. Вариант Определить поперечную силу в сечении 1-1 1) — 39 кн, ) 15 кн, 3) — 7 кн, 4) 4 кн.. Выбрать формулу для изгибающего момента в сечении
44 1) F 1 z 3 F (z 3 ) F 3 (z 3-4), ) -F 1 z 3 + F (z 3 ) F 3 (z 3-4), 3) — F 1 z 3 + F (z 3 3) +F 3 (z 3-4) -М 1, 4) -F 1 z 3 + F (z 3 ) F 3 (z 3-4). 3. Определить величину изгибающего момента в сечении Г (схема к вопросу ), если F 1 = 10 кн, F = 15 кн, F 3 = 18 кн, М 1 = 0 кн м, М = 30 кн м. 1) 59 кн м, ) 9 кн м, 3) 7 кн м, 4) 76 кн м. 4. Из представленных на схеме эпюр выбрать эпюру поперечной силы. 1) А, ) Б, 3) Г, 4) Д. 5. Из представленных в вопросе 4 эпюр выбрать эпюру изгибающих моментов для балки. 1) А, ) Б, 3) В, 4) Е. 44
45 Вариант Определить величину поперечной силы в сечении -. 1) кн, ) 15 кн, 3) 37 кн, 4) 7 кн.. Выбрать формулу для изгибающего момента в сечении ) М 1 + F 1 z 3 F (z 3 4) + М, ) М 1 + F 1 z 3 + F (z 3 4) +М + F 3, 3) М 1 + F 1 z 3 — F (z 3 4) + М + F 3 (z 3-7), 4) М 1 + F 1 z 3 — F (z 3 ) + М. 3. Определить величину изгибающего момента в сечении Г (схема к вопросу ), если М 1 = 100 кн м, М = 50 кн м, F 1 = 10 кн, F = 18 кн, F 3 = 0 кн. 1) 140 кн м, ) 190 кн м, 3) 370 кн м, 4) 150 кн м. 4. Из представленных на схеме эпюр выбрать эпюру поперечной силы для изображённой балки. 45
46 1) Д, ) А, 3) Б, 4) Е. 5. Из представленных в вопросе 4 эпюр выбрать эпюру изгибающих моментов для балки. 1) Б, ) В, 3) Г, 4) Д. Вариант Определить участок поперечного изгиба. 1) 1 участок, ) участок, 3) 3 участок, 4) 4 участок.. Выбрать формулу для определения изгибающего момента в сечении -. y М 1 F F 3 М А Б В Г Д Е F 1 x F 4 м 1 м 3 м 3 м м z 46
47 1) М 1 + F 1 z F (z ), ) — М 1 — F 1 z — F z — М, 3) — М 1 + F 1 z — F (z ), 4) — М 1 + F 1 z — F (z )+F Определить величину изгибающего момента в сечении Г справа (схема к вопросу ), если F 1 = 15 кн, F = кн, F 3 = 37 кн, М 1 = 5 кн м, М = 45 кн м. 1) 359 кн м, ) 179 кн м, 3) 19 кн м, 4) 134 кн м. 4. Из представленных на схеме эпюр выбрать эпюру поперечной силы для балки. 1) В, ) Г, 3) Д, 4) Е. 5. Из представленных в вопросе 4 эпюр выбрать эпюру изгибающих моментов для балки. 1) А, ) Б, 3) Д, 4) Е. 9. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ В БАЛКАХ ПРИ ИЗГИБЕ ОТ НАГРУЗОК Вариант Определить реакцию в опоре В. 47
48 1) 3,6 кн; ) 8,4 кн; 3) 6 кн; 4) 1 кн.. Определить поперечную силу в точке с координатой м. 1). — 4 кн, ) 1, кн, 3) 11 кн, 4) -13,8 кн. 3. Определить изгибающий момент в точке С. D м С 10 кн В 3 м м кн/м А 1 кн м 1) — 4 кн м, ) — 67 кн м, 3) — 55 кн м, 4) — 76 кн м. 4. Из представленных на схеме эпюр выбрать эпюру поперечной силы для балки. 1) 1, ), 3) 3, 4) 5. 48
49 5. Из представленных в вопросе 4 эпюр выбрать эпюру изгибающих моментов для балки. 1) 1, ), 3) 4, 4) 6. Вариант Определить реакцию в опоре В. 1) 11,6 кн; ) 18,75 кн; 3) 30 кн; 4) 47,5 кн.. Определить координату точки z, в которой поперечная сила равна нулю? 1) м; ),3 м; 3) 3,4 м; 4) 5 м. 3. Определить изгибающий момент в точке В. 1) 10 кн м, ) 15 кн м, 3) 5 кн м, 4) 195 кн м. 4. Из представленных на схеме эпюр выбрать эпюру поперечной силы для балки. 49
50 1) 1, ), 3) 3, 4) Из представленных в вопросе 4 эпюр выбрать эпюру изгибающих моментов для балки. 1) 1, ) 4, 3) 5, 4) Определить реакцию в опоре В. Вариант 9.3 1) 37,95 кн; ) 31,05 кн; 3) 6,05кН; 4) 18,95 кн.. В каком сечении балки изгибающий момент максимален? 1) 4 м, ) 4,5 м, 3) 5 м, 4) 6 м. 50
51 3. Определить изгибающий момент в точке В (справа). 1) — 47 кн м, ) — 10 кн м, 3) — 16 кн м, 4) кн м. 4. Из представленных на схеме эпюр выбрать эпюру поперечной силы для балки. 1) 1, ) 3, 3) 4, 4) Из представленных в вопросе 4 эпюр выбрать эпюру изгибающих моментов для балки. 1), ) 3, 3) 4, 4) Определить реакцию в опоре В. Вариант 9.4 1) 3,8 кн; ) 8,6 кн; 3) 38 кн; 4) 41,8 кн. 51
52 . На каком участке бруса поперечная сила равна нулю? 1) 1 участок, ) участок, 3) 3 участок, 4) такого участка нет. 3. Выбрать формулу для определения изгибающего момента на участке (см. схему к вопросу ). y x z 1) 3) z 5 z 43, 8z q ; ) 6 q 43, 8; z 5 z 5 3, 3z q ; 4) 3, 3z q. 4. Из представленных на схеме эпюр выбрать эпюру поперечной силы для балки 1) 1, ), 3) 3, 4) Из представленных в вопросе 4 эпюр выбрать эпюру изгибающих моментов для балки 5
53 1) 1, ), 3) 4, 4) Определить реакцию в опоре В. Вариант 9.5 3,4 кн/м А В 1 м 7 м м 1) 10,71 кн; ) 13,09 кн; 3) 3,8 кн; 4) 3,4 кн.. Определить координату точки z, в которой изгибающий момент достигает максимума или минимума? 1) м, ) 3 м, 3) 4 м, 4) 5 м. 3. Определить изгибающий момент в точке С (слева) (см. схему к вопросу ). 1) -8 кн м, ) 30 кн м, 3) 64 кн м, 4) 104 кн м. 4. Из представленных на схеме эпюр выбрать эпюру поперечной силы для балки. 1) 1, ) 3, 3) 4, 4) 5. 53
54 5. Из представленных в вопросе 4 эпюр выбрать эпюру изгибающих моментов для балки. 1), ) 3, 3) 4, 4) РАСЧЁТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ Вариант Определить поперечную силу в любом сечении на II участке балки. 1) 1 кн, ) 39 кн, 3) 14 кн, 4) — 5 кн.. Вычислить изгибающий момент в сечении С. 5,4 кн 18 кн 4 кн 11,4 кн A В C 3 м 4 м 3 м D 1) 37,8 кн м; ) 7 кн м; 3) — 34, кн м; 4) 4 кн м. 3. Для балки (вопрос ) определить максимальное нормальное напряжение в сечении С. Сечение балки швеллер. 1) 87, МПа; ) 101 МПа; 3) 15 МПа; 4) 178 МПа. 4. При каком поперечном сечении балка выдержит большую нагрузку? 1) А, ) Б, 3) В, 4) Г. 54
55 5. Нормальное напряжение при изгибе в точке В поперечного сечения балки 140 МПа. Определить нормальное напряжение в точке С, 1 h H. 4 H h 1) 110 МПа; ) 55 МПа; 3) 70 МПа; 4) 93,3 МПа. Вариант Определить поперечную силу в любом сечении на II участке бруса. 1) — 0 кн, ) 8 кн, 3) 1 кн, 4) 4 кн.. Вычислить изгибающий момент в сечении С. 1) 6 кн м, ) — кн м, 3) 10 кн м, 4) 5 кн м. 3. Для балки (вопрос ) определить максимальное нормальное напряжение в сечении С. Сечение балки швеллер 16. 1) 47 МПа, ) 1,4 МПа, 3) 79 МПа, 4) 10 МПа. 55
56 4. При каком поперечном сечении балка выдержит большую нагрузку? 1) А, ) Б, 3) В, 4) Г. 5. Нормальное напряжение при изгибе в точке В поперечного сечения балки 60 МПа. Определить нормальное напряжение в точке С. 1 h H 3 1) 10 МПа, ) 60 МПа, 3) 40 МПа, 4) 80 МПа. Вариант Определить поперечную силу в любом сечении на III участке балки. 8 кн М 1 =8 кн м М =10 кн м 1 кн 4 кн м 3 м 4 м м I II III IV 1) 0 кн, ) — 8 кн, 3) -16 кн, 4) 4 кн.. Вычислить изгибающий момент в сечении С. 56
57 1) 6 кн м; ) -5, кн м; 3) 10 кн м; 4) 15 кн м. 3. Для балки (вопрос ) определить максимальное нормальное напряжение в сечении В. Сечение балки швеллер 10. 1) 86 МПа; ) 96 МПа; 3) 149 МПа; 4) 18,4 МПа. 4. При каком поперечном сечении балка выдержит большую нагрузку? 1) А, ) Б, 3) В, 4) Г. 5. Нормальное напряжение при изгибе в точке В поперечного сечения балки 10 МПа. Определить нормальное напряжение в точке С. 1 h H 4 H h 1) 10 МПа, ) 60 МПа, 3) 40 МПа, 4) 80 МПа. Вариант Определить поперечную силу в любом сечении на II участке балки. 1) 18 кн; ) -1,6 кн; 3) 11,4 кн; 4) 4 кн.. Вычислить величину изгибающего момента в сечении D. 57
58 15 кн М 1 =8 кн м 10 кн М =4 кн м 0 кн А В С D Е 3 м м 1,5 м м 1) 94,5 кн м; ) 6,5 кн м; 3) 74,5 кн м; 4) 109,5 кн м. 3. Для балки (вопрос ) определить максимальное нормальное напряжение в сечении D. Сечение балки швеллер 40. 1) 48,5 МПа; ) 97,9 МПа; 3) 10 МПа; 4) 147 МПа. 4. Выбрать вариант поперечного сечения балки, при котором балка выдержит большую нагрузку. 1) А, ) Б, 3) В, 4) Г. 5. Выбрать соответствующую эпюру распределения касательных напряжений по высоте сечения при поперечном изгибе. y 1) А, ) Б, 3) В, 4) Г. о x А Б В Г Вариант Определить поперечную силу в любом сечении на III участке бруса. 58
59 5,4 кн 18 кн 4 кн 11,4 кн I II III 3 м 4 м 3 м 1) 18 кн; ) 1,6 кн; 3) — 11,4 кн; 4) 4 кн..определить изгибающий момент в сечении С (справа). 1) 94,5 кн м; ) — 6,5 кн м; 3) 74,5 кн м; 4) 109,5 кн м. 3. Для балки (вопрос ) определить максимальное нормальное напряжение в сечении С. Сечение балки двутавр 30. 1) 54,7 МПа; ) 67, МПа; 3) 13,4 МПа; 4) 154 МПа. 4. Выбрать вариант поперечного сечения балки, при котором балка выдержит большую нагрузку. 1) А, ) Б, 3) В, 4) Г. 5. Выбрать соответствующую эпюру распределения касательных напряжений по высоте сечения при поперечном изгибе. 59
60 1) А, ) Б, 3) В, 4) Г. 11. СОВМЕСТНОЕ ДЕЙСТВИЕ ИЗГИБА И КРУЧЕНИЯ Вариант Какие напряжения возникают в точке поперечного сечения бруса при действии изгиба с кручением? 1), ), 3) и, 4) однозначного ответа нет.. Какое напряжение называют расчётным (приведенным)? 1) напряжение, равное действующему, ) напряжение равноопасного состояния, 3) напряжение, равное геометрической сумме действующих напряжений, 4) напряжение, равное алгебраической сумме действующих напряжений. 3. Выбрать формулу для определения расчётного момента по гипотезе максимальных касательных напряжений. 1) М изг Т, ) Мизг Т, 3) 4) верный ответ не приведен. изг М 0, 75Т, 3. Выбрать участок вала, где действуют только изгибающий момент и поперечная сила. F r1 F r1 F t 1 F r 1) участок 1, ) участок, 3) участок 3, 4) такого участка нет. 5. В опасном сечении стального бруса круглого поперечного сечения действуют изгибающий момент 500 кн м и крутящий момент 00 кн м. F r F t 60
61 Проверить прочность бруса, если его диаметр 60 мм, а допускаемое напряжение 160 МПа. Расчёт выполнить по IV гипотезе прочности. 1) red. IV adm, ) red. IV adm, 3) red. IV adm, 4) данных недостаточно. Вариант Какие напряжения возникают в поперечном сечении бруса при действии сил F 1 и F. 1), ), 3) и, 4) однозначного ответа нет.. Какое напряжение называют приведённым по заданной гипотезе прочности? 1) напряжение, равное действующему, ) напряжение, равное геометрической сумме действующих напряжений, 3) напряжение, равное алгебраической сумме действующих напряжений, 4) напряжение равноопасного состояния для точки. 3. Выбрать условие для проверки на прочность бруса, изображённого на схеме. N A 1) adm M red 4) red adm Wx y F 1 x T F T M x, ) adm, 3) adm, W. W p 4. По эпюрам изгибающих и крутящих моментов определить расчётный (приведённый) момент в опасном сечении бруса по IV гипотезе прочности. x z 61
62 F F 1 1) 16 кн м; ) 1 кн м; 3) 10,5 кн м; 4) 11,6 кн м. 5. Для вала, изображённого на схеме к вопросу 4, определить диаметр в опасном сечении, если допускаемое напряжение для материала 140 МПа. Расчёт выполнить по IV гипотезе прочности. 1) 65 мм, ) 75 мм, 3) 9 мм, 4) 105 мм. Вариант Для чего служат гипотезы прочности? 1) для определения характера разрушения, ) для определения деформации, 3) для замены сложного напряжённого состояния равноопасным простым, 4) для упрощения расчётов.. Выбрать формулу для определения расчётного напряжения по IV гипотезе прочности. 4) 1), ) red. IV 1. red. IV 3, 3) red. IV red. IV 1 4, 3. Указать на схеме участок вала, где не действует крутящий момент. F r F t F r F r1 F r1 F t1 6
63 1) участок 1, ) участок, 3) участок 3, 4) такого участка нет. 4. По приведенным эпюрам изгибающего и крутящего моментов определить эквивалентный момент в опасном сечении бруса по гипотезе максимальных касательных напряжений. F 1 о 10 Н м R A F М 160 Н м 400 Н м 1) 160 Н м, ) 430 Н м, 3) 50 Н м, 4) 560 Н м. 5. Для вала, изображённого на схеме к вопросу 4, определить диаметр в опасном сечении, если допускаемое напряжение для материала 140 МПа. Расчёт выполнить по IV гипотезе прочности. 1) 0,5 мм; ) 5 мм; 3) 8,5 мм; 4) 31,5 мм. R В Т z M изг Вариант Указать силу на схеме вала, которая вызывает только изгиб 1) F t, ) F r, 3) правильного ответа нет, 4) F t и F r. Ft Ft. Выбрать формулу для определения расчётного напряжения по IV гипотезе прочности. 1), ), 3) 3, 4) Определить максимальный изгибающий момент в поперечном сечении вала, если R A = 1,5 кн, R B = 7,5 кн, F = 15 кн, F = 5 кн, а = 0,3 м. t 1 t 63
64 F t F t F t1 Ft F 1 t 1),5 кн м; ) 3,75 кн м; 3) 4,5 кн м; 4) 6,5 кн м. 4. Определить крутящий момент, действующий на вал (схема к вопросу 3), если диаметр колес d 1 =100мм, d = 300 мм. 1) 0,75 кн м; ) кн м; 3),5 кн м; 4),8 кн м. 5. В опасном сечении стального вала возникают изгибающий момент 5 Н м, и крутящий момент Н м, допускаемое напряжение для материала 80 МПа. Определить диаметр вала, используя гипотезу максимальных касательных напряжений. 1) 9 мм, ) 15 мм, 3) 0 мм, 4) 5 мм. Вариант Указать силу на схеме вала, которая изгибает и скручивает вал. 1) F t, ) F r, 3) правильного ответа нет, 4) F t и F r.. Каким напряженным состоянием по гипотезе прочности заменяют напряжённое состояние в точке бруса при совместном действии изгиба и кручения? 1) плоским двухосным, ) равноопасным одноосным, 3) плоским, суммарным, 4) трёхосным (объёмным). 64
65 3. Выбрать условие прочности для проверки на прочность вала, изображённого на схеме. M x 1) adm Wx T 4) adm W p. Q M red. IV, ) adm, 3) red. IV adm A W x, 4. Определить изгибающий момент в опасном поперечном сечении вала (схема к вопросу 3),если силы F t = 8 кн; F r =,5 кн. Диаметр колеса 60 мм. Длины участков вала определяют из условия а = 0,1 м. 1) 0,15 кн м; ) 0,55 кн м; 3) 0,419 кн м; 4) 0,175 кн м. 5. Проверить прочность вала, если в опасном сечении возникают изгибающий и крутящий моменты. Дано: М изг 50 H м, T 100 H м, d 45 мм, adm 10 МПа. Расчёт выполнить по гипотезе наибольших касательных напряжений. 1) red. III adm, ) red. III adm, 3) red. III adm, 4) данных недостаточно. 1. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ Вариант Что такое критическая сила? 1) максимальная сжимающая сила, при которой стержень сохраняет свою прочность, ) максимальная сжимающая сила, при которой стержень теряет упругость, 3) сила, при которой стержень сохраняет свою устойчивость, 4) максимальная сила, при которой в стержне появляются пластические деформации. 65
66 . Определить приведенную длину стержня для расчёта на устойчивость, если l = 3м. 1) 1,5 м; ),1 м; 3) 3 м; 4) 6 м. 3. От каких параметров сжатого стержня (смотри приведенный график) зависит величина max? 1) от материала, ) от длины стержня, 3) от поперечного сечения, 4) от способа закрепления. 4. Как изменится F cr при замене двутавра 16 двутавром 0 (при прочих равных условиях)? Применима формула Эйлера. 1) уменьшится в раза, ) уменьшится в 4 раза, 3) увеличится в раза, 4) увеличится в 8 раз. 5. Определить F cr для стержня в вопросе. Сечение двутавр 0, материал сталь Е = 10 5 МПа. 1) 61 кн, ) 5 кн, 3) 496 кн, 4) 99 кн. Вариант Выбрать правильную запись условия устойчивости сжатого стержня. Fcr 1) с adm, c, ) cr a b adm, c, 3) c adm, s, A Fc 4) c adm, s. A 66
67 . Как изменится критическая сила при замене прямоугольного сечения на двутавровое сечение? Применима формула Эйлера. 40 1) уменьшится в 5 раз, ) увеличится в 10 раз, 3) уменьшится в 15 раз, 4) уменьшится в 0 раз. 3. Как изменится гибкость стержня при замене схемы крепления концов с варианта А на вариант Б? F 1500 мм А F В 1) уменьшится в раза; ) уменьшится в,86 раза; 3) уменьшится в 4 раза; 4) уменьшится в,4 раза. 4. По какой из приведенных формул следует рассчитывать стержень, изображённый на схема к вопросу 3 (А), если материал сталь, а сечение двутавр 0? EImin 1) F сr l, ) Fсr a b A, 3) F A, 4) расчёт на устойчивость не проводится. сr y 5. Определить допускаемую нагрузку для стержня (вопрос 4), если запас устойчивости трехкратный? Материал сталь Е = 10 5 МПа. 67
68 1) 50 кн; ) 43 кн; 3) 15,3 кн; 4) 84,0 кн. Вариант Выбрать правильную запись условия устойчивости. s 1) Fс Fadm, ) s Fс Fadm, 3) F с c A, 4) F cr A с.. Из перечисленных характеристик материала выбрать характеристику, используемую при расчёте на устойчивость. 1) y, ), 3) E, 4) HB. u 3. Найти гибкость стержня круглого поперечного сечения, если его диаметр 60 мм, длина,4 м, стержень шарнирно закреплён с обоих концов. 1) 640, ) 160, 3) 30, 4) По какой из приведенных формул следует проверить на устойчивость стержень (схема к вопросу 3), если материал стержня сталь, предельная гибкость которой 96? EImin 1) F сr l, ) Fсr a b A, 3) F A, 4) F A. сr с сr y 5. Определить допускаемую нагрузку для стойки. Материал сталь Е = 10 5 МПа, поперечное сечение швеллер 16, коэффициент запаса в расчётах на устойчивость равен 4. Применима формула Эйлера. 1) 17,35 кн; ) 34,7 кн; 3) 68,95 кн; 4) 48,95 кн. 68
69 Вариант Что понимают под устойчивостью сжатых стержней? 1) отсутствие разрушения при сжатии, ) отсутствие опрокидывания, 3) способность сохранять первоначальную форму равновесия, 4) способность восстанавливать исходную форму равновесия.. Как изменится F cr при замене первого способа крепления стержня на второй? 1) увеличится в 4 раза, ) уменьшится в раза, 3) уменьшится в 4 раза, 4) не изменится. 3. Определить величину гибкости для стержня. Сечение швеллер 16, длина l = 5м. 1) 167; ) 155,8; 3) 535; 4) По какой из формул следует рассчитывать на устойчивость стержень на участке? σ cr σ y σ e, ) a b A, 3) A, 4) подходящая формула не приведена. 1) EI l min 1уч. уч. 3уч. λ0 λ max с λ 69
70 5. Устойчив ли стержень, представленный на схеме к вопросу 3? Действующая сжимающая сила 10 кн. Коэффициент запаса в расчётах на устойчивость n s 4, материал сталь, Е = 10 5 МПа. 1) Fadm s Fc, ) Fadm s Fc, 3) Fadm s Fc, 4) данных недостаточно. Вариант Чему равно критическое напряжение для круглого стержня, если s известно, что F c = 8 кн; F adm = 1 кн; F cr = 4 кн; диаметр стержня 50 мм? 1) 4,01 МПа; ) 6,11 МПа; 3) 1, МПа; 4),4 МПа.. Как изменится критическая сила, если длину стойки увеличить в 3 раза? Применима формула Эйлера. 1) увеличится в 9 раз, ) уменьшится в 9 раз, 3) уменьшится в 6 раз, 4) увеличится в 3 раза. 3. Определить гибкость стального стержня. Поперечное сечение двутавр 18. 1) 7,3; ) 54,6; 3) 76,4; 4) 106,4. 4. По какой из формул следует рассчитывать устойчивость стержня на участке 3? σ cr σ y σpr 1) с y 1уч. уч. 3уч. λ 0 λ max E EImin c a b, 3) c, 4) c. A, ) λ 70
71 5. Устойчив ли стержень (схема к вопросу 3)? Действующая сжимающая сила 134 кн, материал сталь, Е = 10 5 МПа, сечение двутавр 18, коэффициент запаса в расчётах на устойчивость n s 3. Применима формула Эйлера. 1) F Fadm, ) требуется. s s adm F F, 3) F F s adm КОДЫ ПРАВИЛЬНЫХ ОТВЕТОВ, 4) расчёт на устойчивость не Основные положения, метод сечений, напряжения Тема 1 Вопросы: Вариант Вариант Вариант Вариант Вариант Расчёты на прочность при растяжении и сжатии Тема 3 Вопросы: Вариант Вариант Вариант Вариант Вариант Основные механические характеристики Тема Вопросы: Вариант Вариант Вариант Вариант Вариант Практические расчёты на срез и смятие Тема 4 Вопросы: Вариант 1 3 Вариант 3 3 Вариант Вариант 4 4 Вариант Геометрические характеристики плоских сечений Тема 5 Вопросы: Вариант Вариант Вариант Вариант Вариант Кручение 1 Тема 6 Вопросы: Вариант Вариант 4 1 Вариант Вариант Вариант
72 Кручение Тема 7 Вопросы: Вариант Вариант Вариант Вариант Вариант Определение внутренних усилий в балках при изгибе от сосредоточенных нагрузок Тема 8 Вопросы: Вариант Вариант Вариант Вариант Вариант Определение внутренних усилий в балках при изгибе нагрузок Тема 9 Вопросы: Вариант Вариант 3 4 Вариант Вариант Вариант Расчёты на прочность при изгибе Тема 10 Вопросы: Вариант Вариант Вариант Вариант Вариант Совместное действие изгиба и кручения Тема 11 Вопросы: Вариант Вариант Вариант Вариант Вариант Устойчивость сжатых стержней Тема 1 Вопросы: Вариант Вариант Вариант Вариант Вариант
💥 Видео
Математика без Ху!ни. Как вычислить определитель.Скачать
Формула ЖуравскогоСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Решение системы уравнений методом ГауссаСкачать

Ядро сечения теорияСкачать

Математика без Ху!ни. Метод Гаусса.Скачать