По группе 10 заводов производящих однородную продукцию получено уравнение регрессии (4 видео)

По группе 10 заводов производящих однородную продукцию получено уравнение регрессии себестоимости единицы продукции y (тыс

Реферат.Справочник
Решенные задачи по эконометрике
По группе 10 заводов производящих однородную продукцию получено уравнение регрессии себестоимости единицы продукции y (тыс

Содержание

Условие
Решение
Задача 1
Тема 11. Нелинейные регрессии и их линеаризация
🌟 Видео

Условие

По группе 10 заводов, производящих однородную продукцию, получено уравнение регрессии себестоимости единицы продукции y (тыс. руб.) от уровня технической оснащенности x (тыс. руб.): y=20+700x, R2 = 0,18. Определите F-критерий Фишера. Сделайте выводы.

Решение

Проверка значимости линейной регрессии в целом: F=R21-R2∙n-k-1k=0.181-0.18∙10-21=1,76 Fтабл (0.05;1;8) = 5,32 Так как F 50% текста решения задач недоступно

Оплатите решение задач или закажите уникальную работу на похожую тему

Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Задача 1

По группе 10 заводов, производящих однородную продукцию, получено уравнение регрессии себестоимости единицы продукции у (тыс. руб.) от уровня технической оснащённости х (тыс. руб.):

. Доля остаточной дисперсии в общей составила 0,19.

а) коэффициент эластичности, предполагая, что стоимость активных производственных фондов составляет х=200 тыс. руб.;

б) индекс корреляции;

в) F – критерий Фишера. Сделайте выводы.

а)

Показывает если уровень технической оснащённости (х) увеличивается

на 1 %, то себестоимости единицы продукции (у) уменьшается на 0,149 %.

б)

Связь между у и х сильная и прямая.

F табличное =4,96

Рассчитав F критерий Фишера увидим, что F табличное =4,96> F расчетное =3,75 следовательно линейная модель статистически незначима при α=0,05.

Таблица 1. Показатели для расчёта линейной функции y=a+b·x

Рассчитав уравнение линейной функции видно, что если х увеличиться на 1 рубль, то у уменьшиться на 0,54 %.

Коэффициент корреляции R показывает, что связь между х и у прямая 0,84%

Коэффициент детерминации R2 показывает, что качество модели высокое и вариация результата у на 71% объясняется вариацией фактора х.

Рассчитав F критерий Фишера увидим, что F табличное =4,41 Fтабл. Þ уравнение множественной регрессии статистически значимо.

Fx1 > Fтабл. Þ фактор х1 целесообразно включать в модель т. к. он увеличивает качество модели

Fx2 > Fтабл. Þ фактор х2 увеличивает качество модели Þ его необходимо включать в уравнение.

1. Эконометрика: Учебник под ред. , М: «Финансы и статистика», 2001;

2. «Практикум по эконометрике» под ред. , М: «Финансы и статистика», 2001;

3. Мхитарян, Айвазян «Прикладная статистика и основы эконометрики». М: Юнити, 1998;

4. , , «Эконометрика. Начальный курс: учебник». М: Дело, 2001;

5. К. Доугерти. «Введение в эконометрику». М: Инфра-М. Норма, 1999.

Видео:Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

Тема 11. Нелинейные регрессии и их линеаризация

Аннотация.Данная тема раскрывает особенности построения нелинейных моделей регрессии.

Ключевые слова.Нелинейная регрессия, индекс корреляции, коэффициент эластичности, подход Бокса-Кокса.

Методические рекомендации по изучению темы

· Тема содержит лекционную часть, где даются общие представления по теме.

· В качестве самостоятельной работы предлагается ознакомиться с решениями типовых задач, выполнить практические задания и ответить на вопросы для самоконтроля.

· Для проверки усвоения темы имеется тест для самоконтроля.

· Для подготовки к экзамену имеется контрольный тест.

Рекомендуемые информационные ресурсы:

2. Эконометрика: [Электронный ресурс] Учеб. пособие / А.И. Новиков. — 3-e изд., испр. и доп. — М.: ИНФРА-М, 2014. — 272 с.: (http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=1#none) С. 41-45.

3.Уткин, В. Б. Эконометрика [Электронный ресурс] : Учебник / В. Б. Уткин; Под ред. проф. В. Б. Уткина. — 2-е изд. — М.: Издательско-торговая корпорация «Дашков и К°», 2012. — 564 с.

(http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=4#none) С. 383-399.

4. Эконометрика. Практикум: [Электронный ресурс] Учебное пособие / С.А. Бородич. — М.: НИЦ ИНФРА-М; Мн.: Нов. знание, 2014. — 329 с. (http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=4#none) С.172-174.

Глоссарий

Бокса-Кокса подход – способ подбора линеаризующего преобразования.

Индекс корреляции—показатель корреляции, который определяется для нелинейных регрессий.

Коэффициент эластичности показывает, на сколько процентов изменится результативный признак Y, если факторный признак изменится на 1 процент.

Линеаризация нелинейных моделей – процедура, которая заключается в преобразовании или переменных, или параметров модели, или в комбинации этих преобразований.

Нелинейная модель, внутренне линейная, с помощью преобразований может быть приведена к линейному виду.

Нелинейная модель, внутренне нелинейная, не может быть сведена к линейной функции.

Вопросы для изучения

1. Классы и виды нелинейных регрессий.

2. Линеаризация нелинейных моделей. Выбор формы модели.

3. Индекс корреляции. Подбор линеаризующего преобразования (подход Бокса-Кокса).

Классы и виды нелинейных регрессий. Различают два класса нелинейных регрессий: регрессии, нелинейные относительно включенных в анализ объясняющих переменных; регрессии, нелинейные по оцениваемым параметрам. Нелинейная модель, внутренне линейная, с помощью преобразований может быть приведена к линейному виду. Нелинейная модель, внутренне нелинейная, не может быть сведена к линейной функции. При анализе нелинейных регрессионных зависимостей наиболее важным вопросом применения классического МНК является способ их линеаризации.

Линеаризация нелинейных моделей. Выбор формы модели. В нелинейных зависимостях, не являющихся классическими полиномами, обязательно проводится предварительная линеаризация, которая заключается в преобразовании или переменных, или параметров модели, или в комбинации этих преобразований. Рассмотрим некоторые классы таких зависимостей.

Рис. 11.1. Способы линеаризации

Замена переменных заключается в замене нелинейных объясняющих переменных новыми линейными переменными и сведении нелинейной регрессии к линейной. Логарифмирование обеих частей уравнения применяется обычно, когда мультипликативную модель необходимо привести к линейному виду. К классу степенных функций относятся: кривые спроса и предложения, производственная функция Кобба-Дугласа, кривые освоения для характеристики связи между трудоемкостью продукции и масштабами производства в период освоения и выпуска нового вида изделий, зависимость валового национального дохода от уровня занятости.

Индекс корреляции. Подбор линеаризующего преобразования (подход Бокса-Кокса). Любое уравнение нелинейной регрессии, как и линейной зависимости, дополняется показателем корреляции, который в данном случае называется индексом корреляции:

Здесь — общая дисперсия результативного признака y, — остаточная дисперсия, определяемая по уравнению нелинейной регрессии . По-другому можно записать так:

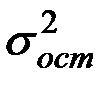
Следует обратить внимание на то, что разности в соответствующих суммах и берутся не в преобразованных, а в исходных значениях результативного признака. Иначе говоря, при вычислении этих сумм следует использовать не преобразованные (линеаризованные) зависимости, а именно исходные нелинейные уравнения регрессии. Величина R находится в границах , и чем ближе она к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.

Если разные модели используют разные функциональные формы для зависимой переменной, то проблема выбора модели становится более сложной, так как нельзя непосредственно сравнивать коэффициенты R 2 или суммы квадратов отклонений. Например, нельзя сравнивать эти статистики для линейного и логарифмического вариантов. Пусть в линейной модели в качестве зависимой переменной используется заработок, а в нелинейной – логарифм заработка. Тогда R 2 в одном уравнении измеряет объясненную регрессией долю дисперсии заработка, а в другом — объясненную регрессией долю дисперсии логарифма заработка. В случае, если значения R 2 для двух моделей близки друг к другу, проблема выбора усложняется. Здесь следует использовать тест Бокса – Кокса. При сравнении моделей с использованием в качестве зависимой переменной y и lny проводится такое преобразование масштаба наблюдений y, при котором можно непосредственно сравнивать суммы квадратов отклонений в линейной и логарифмической моделях. Здесь выполняются следующие шаги. Вычисляется среднее геометрическое значений y в выборке. Оно совпадает с экспонентой среднего арифметического логарифмов y. Все значения y пересчитываются делением на среднее геометрическое, получаем значения y*. Оцениваются две регрессии: для линейной модели с использованием y* в качестве зависимой переменной и для логарифмической модели с использованием ln y* вместо ln y. Во всех других отношениях модели должны оставаться неизменными. Теперь значения СКО для двух регрессий сравнимы, и модель с меньшей остаточной СКО обеспечивает лучшее соответствие исходным данным. Для проверки, обеспечивает ли одна из моделей значимо лучшее соответствие, можно вычислить величину (n/2)lnz, где z – отношение значений остаточной СКО в перечисленных регрессиях. Эта статистика имеет распределение хи – квадрат с одной степенью свободы. Если она превышает критическое значение при выбранном уровне значимости α, то делается вывод о наличии значимой разницы в качестве оценивания.

Величина коэффициента эластичности показывает, на сколько процентов изменится результативный признак Y, если факторный признак изменится на 1 %:

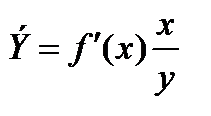
В заключение приведем формулы расчета коэффициентов эластичности для наиболее распространенных уравнений регрессии:

Вид уравнения регрессии	Коэффициент эластичности

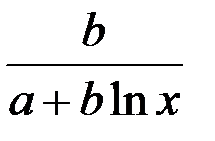Вопросы и задания для самоконтроля

1. Какие модели являются нелинейными относительно: а) включаемых переменных; б) оцениваемых параметров?

2. Какие преобразования используются для линеаризации нелинейных моделей?

3. Чем отличается применение МНК к моделям, нелинейным относительно включаемых переменных, от применения к моделям, нелинейным по оцениваемым параметрам?

4. Как определяются коэффициенты эластичности по разным видам регрессионных моделей?

5. Какие показатели корреляции используются при нелинейных соотношениях рассматриваемых признаков?

6. В каких случаях используют обратные и степенные модели?

Задача 1.По группе предприятий, производящих однородную продукцию известно, как зависит себестоимость единицы продукции (Y) от факторов, приведенных в таблице:

Признак-фактор	Уравнение парной регрессии	Среднее значение фактора
Объем производства, млн. руб.
Трудоемкость единицы продукции, чел/час
Оптовая цена за 1т энергоносителя, , млн. руб.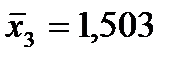
Доля прибыли, изымаемая государством, ,%

1) определить с помощью коэффициентов эластичности силу влияния каждого фактора на результат;

2) ранжировать факторы по силе влияния на результат.

Задача 2. По группе из 10 заводов, производящих однородную продукцию, получено уравнение регрессии себестоимости единицы продукции (тыс. руб) от уровня технической оснащенности (тыс. руб.)