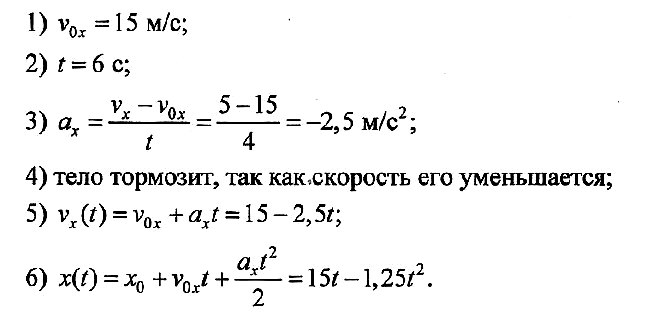- п.1. Равноускоренное движение
- п.2. Ускорение
- п.3. Уравнение скорости и график скорости при равноускоренном прямолинейном движении
- п.4. Определение пути и перемещения по графику скорости
- п.5. Задачи
- Вычисление перемещения по графику проекции скорости
- Теория
- Задачи
- По графику скорости определите ускорение тела и запишите уравнение скорости и перемещения
- Краткое пояснение для решения ЗАДАЧИ на Прямолинейное равноускоренное движение.
- 29 Комментарии
- Добавить комментарий Отменить ответ
- Конспекты по физике:
- 7 класс
- 8 класс
- 9 класс
- 10-11 классы
- Найти конспект:
- О проекте
- 💡 Видео
п.1. Равноускоренное движение
Если тело начинает двигаться из состояния покоя, оно набирает скорость не мгновенно, а в течение некоторого времени. Аналогично происходит при торможении: тело останавливается не сразу, а теряя скорость постепенно.
Примеры равноускоренного движения:
- скатывание велосипеда с горки, скатывание санок с горки;
- старт и торможение автомобиля, автобуса, трамвая, поезда;
- падение на землю камня, ракеты, метеорита.
Это интересно
Время разгона от 0 до 100 км/ч – одна из основных характеристик современных автомобилей.
| Марка автомобиля | Время разгона, с | |
| Nissan GTR Nismo |  | 2,9 |
| BMW M5 F90 |  | 2,8 |
| Porsche 918 Spyder |  | 2,6 |
п.2. Ускорение
В системе СИ (см. §2 данного справочника) скорость измеряется в метрах в секунду, а время – в секундах. Поэтому:
При описании прямолинейного движения мы переходим от векторов к проекциям на ось ОХ (см. §8 данного справочника).
п.3. Уравнение скорости и график скорости при равноускоренном прямолинейном движении
Для проекции скорости на ось ОХ в произвольный момент времени можем записать: $$ v_x(t)=v_+a_x t $$ Сравним полученное уравнение с уравнением прямой (y(x)=kx+b ) (см. §38 справочника по алгебре для 7 класса).
В уравнении скорости роль углового коэффициента (k) играет проекция ускорения (a_x), а роль свободного члена (b) – начальная скорость (v_).
Пример построения графика скорости
1-й участок пути. Пусть автомобиль начал движение из состояния покоя с ускорением 4 м/с 2 . Направим ось ОХ в направлении ускорения и получим уравнение скорости: $$ v_=0, a_x=4frac<text>, v_x(t)=0+4t=4t $$ Через 5 с скорость автомобиля станет равной (v_x(5)=4cdot 5=20) м/с.
2-й участок пути. Пусть автомобиль, набрав эту скорость, проехал с ней без ускорения в течение 10 с. На этом участке уравнение скорости: $$ a_=0, v_x(t)=20frac<text>, 5 cleq tlt 15 c $$ Скорость не меняется, автомобиль движется прямолинейно равномерно.
3-й участок пути. Наконец, на последнем участке пути, автомобиль тормозил с ускорением 5 м/с 2 до полной остановки. Тогда уравнение скорости на этом участке: $$ v_=20frac<text>, a_x=5frac<text>, v_x(t)=20-5t $$ Проекция ускорения при торможении отрицательна. Скорость станет равна 0 через 4 с после начала торможения, автомобиль остановится.
Опишем полностью движение на всех участках: $$ v_x(t)= begin 4t, 0leq tlt 5\ 20, 5leq tlt 15\ 20-5t, 15leq tleq 19 end $$ И построим график:
Участок AB соответствует разгону автомобиля от 0 до 20 м/с, участок BC — равномерному движению со скоростью 20 м/с, участок CD — торможению от 20 м/с до 0.
п.4. Определение пути и перемещения по графику скорости
В §10 данного справочника мы рассматривали неравномерное прямолинейное движение, которое можно разбить на отдельные равномерные участки. Для такого движения путь равен сумме модулей площадей участков, определенных по графику скорости. А перемещение также равно сумме площадей, но уже с учетом знака.
Этот подход можно расширить на любое прямолинейное движение.
Пример определения пути и перемещения по графику скорости
Для построенного выше графика скорости автомобиля получаем следующие участки:
1) ΔABE, его площадь равна $$ s_1=frac12 AEcdot BE=frac12cdot 5cdot 20=50 (м) $$ 2) прямоугольник EBCF, его площадь равна $$ s_2=EFcdot BE=10 cdot 20=200 (м) $$ 3) ΔCFD, его площадь равна $$ s_2=frac12 FDcdot GF=frac12cdot 4cdot20=40 (м) $$ Весь пройденный путь: $$ s=s_1+s_2+s_3=50+200+40=290 (м) $$ Скорость автомобиля все время оставалась положительной (направление движения не менялось), поэтому величина перемещения равна пройденному пути: $$ triangle x=s=290 (м) $$
п.5. Задачи
Задача 1. За 1 мин автобус увеличил скорость с 28,8 км/ч до 72 км/ч. Найдите его ускорение, постройте график зависимости скорости от времени.
Направим ось ОХ по направлению движения автобуса. Автобус направления движения не меняет, и проекции ускорения и скорости все время положительны и по величине равны значениям величин: $$ a_x=a, v_x=v $$ Поэтому ускорение равно: $$ a=frac $$ Получаем: $$ a=frac=0,2 left(fracright) $$ Уравнение зависимости скорости от времени: begin v(t)=v_0+at\ v(t)=8+0,2t end График:
Ответ: 0,2 м/с 2
Задача 2. Поезд двигался прямолинейно равномерно со скоростью 18 км/ч, а в процессе торможения – равноускоренно и остановился через 10 с. Найдите модуль ускорения. Постройте график зависимости скорости от ускорения, найдите пройденный поездом путь за все время торможения.
Дано:
(v_0=18 км/ч=5 м/с)
(v=0)
(t=10 с)
__________________
(a, s-?)
Направим ось ОХ по направлению скорости (v_0). Тогда проекция ускорения: $$ a_x=frac, a_x=frac=-0,5 (м/с^2) $$ Проекция при торможении отрицательна.
Величина (модуль) ускорения: $$ a=|a_x|=0,5 м/c^2 $$ Зависимость скорости от времени: begin v(t)=v_0+a_x t\ v(t)=5-0,5t end График:
Пройденный путь равен площади треугольника ΔABC: $$ s=frac12 ACcdot BC=frac12cdot 5cdot 10=25 (м) $$ Ответ: 0,5 м/с 2 ; 25 м
Задача 3*. С каким ускорением двигался автомобиль, если его скорость выросла с 36 км/ч до 72 км/ч на пути длиной 600 м? Постройте график зависимости скорости от времени, найдите время движения и путь с помощью графика, проверьте полученное значение пути.
Дано:
(v_0=36 км/ч=10 м/с)
(v=72 км/ч=20 м/с)
(s=600 м)
__________________
(a-?, t-?)
Ускорение равно: (a=frac). Откуда время равно: (t=frac)
Средняя скорость на всем пути: (v_=frac)
Весь путь: $$ s=v_t=fraccdotfrac=frac $$ Значит, ускорение равно: $$ a=frac $$ Подставляем: $$ a=frac=0,25 left(fracright) $$ Уравнение зависимости скорости от времени: begin v(t)=v_0+at\ v(t)=10+0,25t end График:
Скорость достигает значения (v=20 м/с) в момент времени (t=40 с).
Значит, время движения 40 с.
Путь по графику скорости равен площади четырехугольника ABCD. begin S_=S_+S_=frac12 AEcdot EB+AEcdot AD=frac12cdot 40cdot 10+40cdot 10=200+400=600 (м)\ s=600 м end Найденное значение пути совпадает с условием задачи. Все параметры движения найдены верно.
Ответ: 0,25 м/с 2 ; 40 c
Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Вычисление перемещения по графику проекции скорости
Из кодификатора по физике, 2020.
«1.1.3. Вычисление перемещения по графику зависимости υ(t).»
Видео:Расчет ускорения по графикуСкачать
Теория
Пусть задан график зависимости проекции скорости от времени t (рис. 1).
Проекция перемещении тела за промежуток времени от до численно равна по величине площади фигуры, ограниченной графиком , осью времени 0t и перпендикулярами к и (см. рис. 1, площадь выделена штриховкой).
Проекцию перемещения на ось 0Х будем считать:
— положительной, если проекция скорости на данную ось будет положительной (тело движется по направлению оси) (см. рис. 1);
— отрицательной, если проекция скорости на данную ось будет отрицательной (тело движется против оси) (рис. 2).
Путь s может быть только положительным:
Напоминаем формулы для расчета площадей фигур:
Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Задачи
Задача 1. По графику проекции скорости тела (рис. 3) определите проекцию его перемещения между 1 и 5 с.
Решение. Проекция перемещения за промежуток времени Δt= – =5с–1с=4c численно равна площади фигуры, ограниченной графиком , осью времени 0t и перпендикулярами к с и с (рис. 4, площадь выделена штриховкой). Фигура ABCD — это трапеция, ее площадь равна
где DC = Δt = 4 c, AD = 3 м/c, BC = 5 м/c. Тогда S = 16 м.
Проекция перемещения 0′ alt=’_>0′ />, т.к. проекция скорости 0′ alt=’_>0′ />.
м.
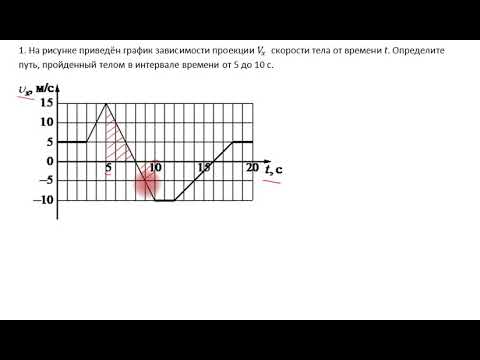
Задача 2. Автомобиль движется по прямой улице вдоль оси X. На рисунке 5 представлен график зависимости проекции скорости автомобиля от времени. Определите путь, пройденный автомобилем в течение указанных интервалов времени.
| Интервал времени | Путь |
| от 0 до 10 с | Ответ: м. |
| от 30 до 40 с | Ответ: м. |
В бланк ответов перенесите только числа, не разделяя их пробелом или другим знаком.
Решение. Путь за промежуток времени Δt = – численно равна площади фигуры, ограниченной графиком осью времени 0t и перпендикулярами к и .
На интервале [0 с, 10 с] ищем площадь треугольника (рис. 6).
где a = 20 м/c, . Тогда м.
Путь равен значению площади (путь всегда положительный, т.е. s > 0).
На интервале [30 с, 40 с] ищем площадь трапеции (см. рис. 6).
где a = 10 м/c, b = 15 м/c, h = Δt = 40 c – 30 с = 10 с. Тогда м.
Задача 3. Определите за первые 4 с (рис. 7):
а) проекцию перемещения тела;
б) пройденный путь.
Ответ: а) ____ м; б) ____ м.
Решение. Проекция перемещения за время (пер-вые 4 с) численно равна площади фигуры, ограниченной графиком , осью времени 0t и перпендикулярами к с и с (рис. 8, площадь выделена штриховкой).
Так как при с проекция скорости поменяла знак, то получили две фигуры, два треугольника, площади которых равны:
а) Проекция перемещения 0′ alt=’_>0′ />, т.к. проекция скорости 0′ alt=’_>0′ />; проекция перемещения , т.к. проекция скорости . В итоге получаем: 45м — 5м = 40 м. б) Путь равен значению площади (путь всегда положительный, т.е. s>0).
, s = 45 м + 5 м = 50 м.
Задача 4. График зависимости проекции скорости материальной точки, движущейся вдоль оси 0Х, от времени изображен на рисунке 9. Определите перемещение точки, которое она совершила за первые 6 с.
Решение. Проекция перемещения за время (пер-вые 6 с) численно равна площади фигуры, ограниченной графиком , осью времени 0t и перпендикулярами к и (рис. 10, площадь выделена штриховкой).
Так как при и проекция скорости меняет знак, то получили три фигуры, три треугольника, площади которых равны:
Проекция перемещения 0′ alt=’_>0′ />, т.к. проекция скорости 0′ alt=’_>0′ />.
Проекция перемещения , т.к. проекция скорости . Проекция перемещения 0′ alt=’_>0′ />, т.к. проекция скорости 0′ alt=’_>0′ />. В итоге получаем:
Видео:Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать

По графику скорости определите ускорение тела и запишите уравнение скорости и перемещения
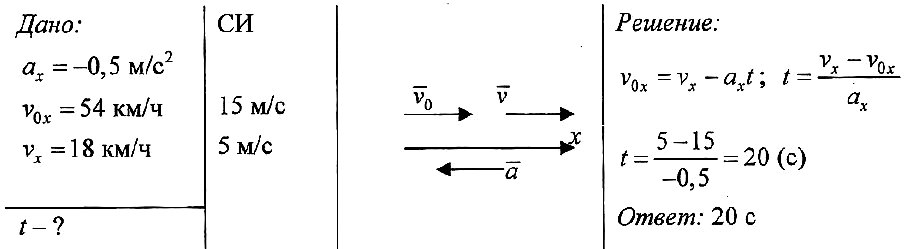
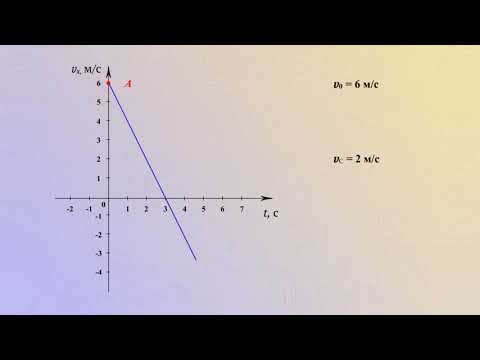
Задача № 1. Автомобиль, двигаясь с ускорением –0,5 м/с 2 , уменьшил свою скорость от 54 до 18 км/ч. Сколько времени ему для этого понадобилось?
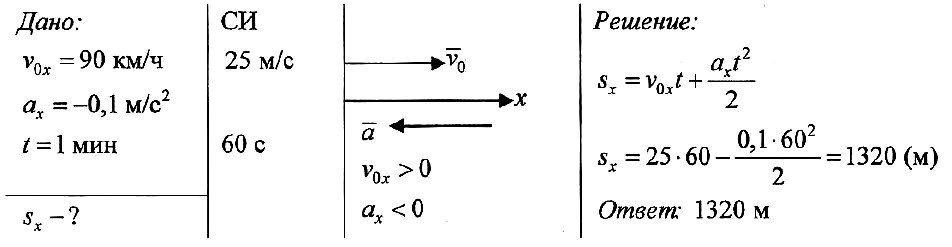
Задача № 2. При подходе к станции поезд начал торможение с ускорением 0,1 м/с 2 , имея начальную скорость 90 км/ч. Определите тормозной путь поезда, если торможение длилось 1 мин.
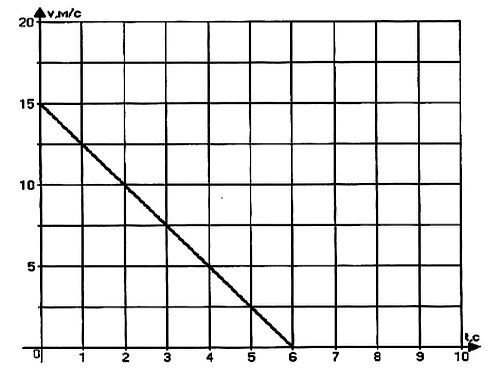
Задача № 3. По графику проекции скорости определите: 1) начальную скорость тела; 2) время движения тела до остановки; 3) ускорение тела; 4) вид движения (разгоняется тело или тормозит); 5) запишите уравнение проекции скорости; 6) запишите уравнение координаты (начальную координату считайте равной нулю).
Решение:
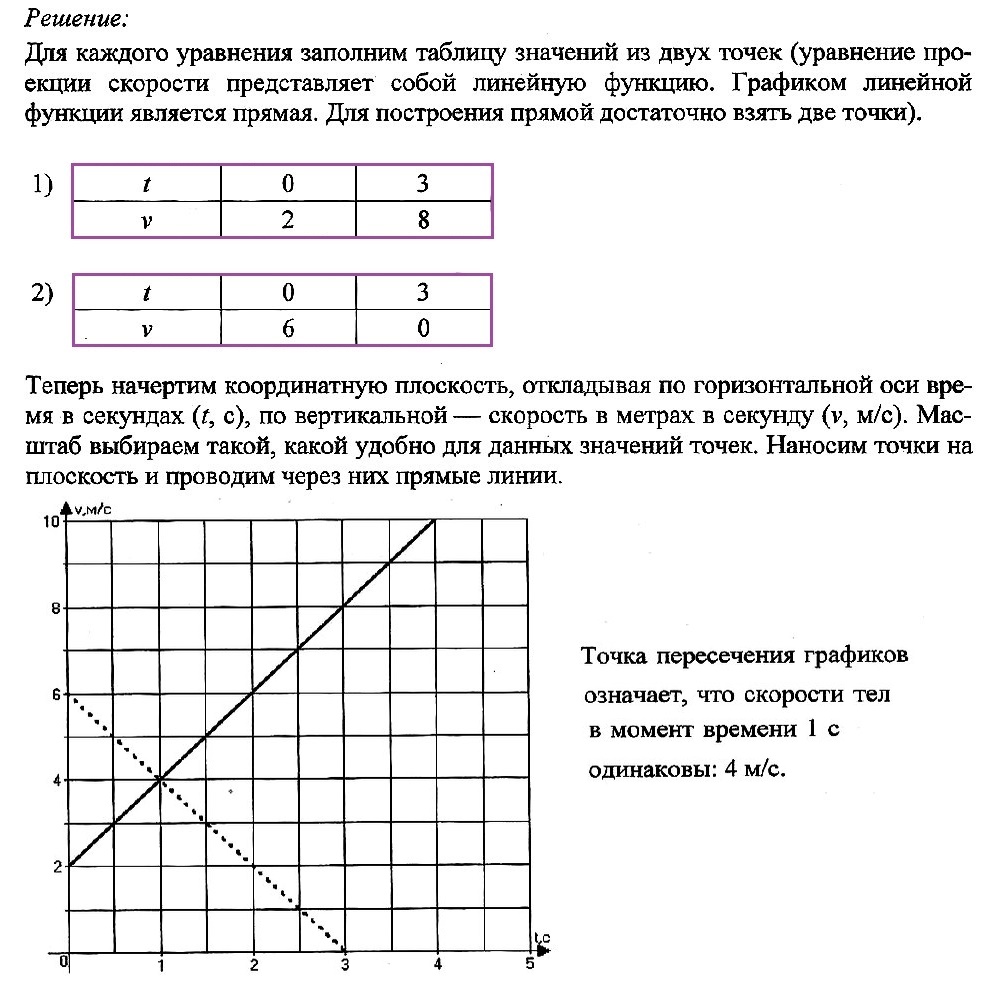
Задача № 4. Движение двух тел задано уравнениями проекции скорости:
v1x(t) = 2 + 2t
v2x(t) = 6 – 2t
В одной координатной плоскости постройте график проекции скорости каждого тела. Что означает точка пересечения графиков?
Задача № 5. Движение тела задано уравнением x(t) = 5 + 10t — 0,5t 2 . Определите: 1) начальную координату тела; 2) проекцию скорости тела; 3) проекцию ускорения; 4) вид движения (разгоняется тело или тормозит); 5) запишите уравнение проекции скорости; 6) определите значение координаты и скорости в момент времени t = 4 с . Сравним уравнение координаты в общем виде с данным уравнением и найдем искомые величины.
Решение:
Задача № 6. Вагон движется равноускоренно с ускорением -0,5 м/с 2 . Начальная скорость вагона равна 54 км/ч. Через сколько времени вагон остановится? Постройте график зависимости скорости от времени.
Задача № 7. Самолет, летевший прямолинейно с постоянной скоростью 360 км/ч, стал двигаться с постоянным ускорением 9 м/с 2 в течение 10 с в том же направлении. Какой скорости достиг самолет и какое расстояние он пролетел за это время? Чему равна средняя скорость за время 10 с при ускоренном движении?
Задача № 8. Трамвай двигался равномерно прямолинейно со скоростью 6 м/с, а в процессе торможения — равноускоренно с ускорением 0,6 м/с 2 . Определите время торможения и тормозной путь трамвая. Постройте графики скорости v(t) и ускорения a(t).
Задача № 9. Тело, имея некоторую начальную скорость, движется равноускоренно. За время t = 2 с тело прошло путь S = 18 м , причём его скорость увеличилась в 5 раз. Найти ускорение и начальную скорость тела.
Задача № 10. (повышенной сложности) Прямолинейное движение описывается формулой х = –4 + 2t – t 2 . Опишите движение, постройте для него графики vx(t), sx(t), l(t) .
Задача № 11. ОГЭ Поезд, идущий со скоростью v0 = 36 км/ч , начинает двигаться равноускоренно и проходит путь S = 600 м , имея в конце этого участка скорость v = 45 км/ч . Определить ускорение поезда а и время t его ускоренного движения.
Краткое пояснение для решения
ЗАДАЧИ на Прямолинейное равноускоренное движение.
Равноускоренным движением называется такое движение, при котором тело за равные промежутки времени изменяет свою скорость на одну и ту же величину. Движение, при котором скорость равномерно уменьшается, тоже считают равноускоренным (иногда его называют равнозамедленным).
Величины, участвующие в описании равноускоренного движения, почти все векторные. При решении задач формулы записывают обычно через проекции векторов на координатные оси. Если тело движется по горизонтали, ось обозначают буквой х, если по вертикали — буквой у.
Если векторы скорости и ускорения сонаправлены (их проекции имеют одинаковые знаки), тело разгоняется, т. е. его скорость увеличивается. Если же векторы скорости и ускорения противоположно направлены, тело тормозит.
Это конспект по теме «ЗАДАЧИ на Прямолинейное равноускоренное движение с решениями». Выберите дальнейшие действия:
29 Комментарии
«отрицательного ускорения» не бывает. Если движущееся тело снижает скорость-вступает в силу 3-й Закон Ньютона: F/m равно, или больше S/tt. Ньютон пытался уравнять ускорения S/tt и F/m, но ошибка в формуле S=att/2 не позволяла . Ошибку эту он сделал, когда искал ускорение свободного падения «яблока…» Конечная скорость-(9,8…) это НЕ at! at-это СРЕДНЯЯ скорость! Она равна (0+V конечная)/2.
V средняя=at. Vконечная=2at. S=(0+2at)/2*t. S=att (и-НИКАКИХ «/2)!
…..Если тело весом (массой) m кг., прошло путь S за время t, то ускорения S/tt=F/m. Искать просто ускорение- бессмысленно. Оно должно помочь найти S,t,F,m,V… Задача: камень весом 25 кг. передвинули на 40 м. за минуту. Вопрос: какую приложили силу- (F) ?
Решение: 40/3600=F/25. Ответ: 0,28 км.м/с. («крутящий момент»)
Задача: этот-же камень, с таким-же «упорством» тащили …100 м. Вопрос: t ? Решение: 100/tt=0,28/25. Ответ: 1,5 минуты (95 секунд).
«Законы» Ньютона пора пересмотреть… (при равномерном движении — НЕТ ускорения. А СРЕДНЯЯ скорость? А из неё и находим ускорение!)
При решении задач нельзя отнимать «скорость от скорости». Всякое движение -это энергия и время. И то и другое не может иметь знак «-«. Время не может пойти «вспять». И =Энергия. Она или есть, или её нет. S/tt=F/m -это значит, материя со временем переходит в энергию, а энергия со временем переходит в материю. ПРИРОДА- ВЕЧНА !
Спасибо за альтернативную точку зрения, не указанную в школьных учебниках физики. Надеюсь, это поможет учащимся расширить свой кругозор в области физики.
Ускорение — это вектор, а он отрицательным быть не может. Но вот проекция ускорения очень даже может быть отрицательной. И, прямо скажем, я не пойму что Вы тут написали, но попахивает каким-то бредом. Хотя бы потому, что at — это приращение скорости, а средняя скорость — это перемещение деленное на время движения, или путь на время движения, если интересует средняя ПУТЕВАЯ скорость. Деление же на 2, в уравнении движения возникает из-за правил интегрирования, которые говорят о том, что интеграл at по dt равен 0.5at^2/
«если тело прошло путь S за время t — график движения НЕ влияет ни на СРЕДНЮЮ скорость, ни на ускорение». А это значит, что не всегда «а» изменяет. скорость. При равномерном движении «а» такое-же, как и при любом движении, потому -что «Ускорение»- это ЭНЕРГИЯ, затраченная на движение, и она эквивалентна изменению скорости. S/tt. Будем считать, что это изменение скорости. Но F/m- это ЭНЕРГИЯ ! И она влияет на изменение скорости, измеряется так-же: «м/сек.сек.»
При решении задач на движение надо движение перевести в СРЕДНЮЮ скорость. А из НЕЁ и искать «ускорение».
У «яблока…» V нач.=0, V конеч.=9,8 м/с. V средняя=(0+9,8):2 V ср.=4,9 м/сек. S=V средняя (!)*t. 4,9*1=4,9 м.
«СРЕДНЯЯ скорость»-это «at». (при любом графике движения). «Конечная» скорость =2at. S=(0+2at)/2*t. S=a*tt, или at*t.
Задачка:… V нач.=10 м/с. V кон.=50 м/с. t=10 секунд. S=? a=? Решение:
Грубейшая ошибка: найти «а» : (50-10)/10. «а»=4 м/сек.сек. S=a*tt. 4*100=400 м.
Правильно будет так: (10+50)/2=30 м/с. Это-СРЕДНЯЯ скорость.. «а»=30/10. а=3 м/сек.сек. S=: V ср.*t=300 м. ; а*tt. 3*100=300 м S/tt=F/m. Ньютон ДОЛЖЕН был вывести такую формулу, но из-за ошибки «att/2» не смог…. S=a*tt = (at*t).
(не «заморачивай-те» головы студентов интегралами).
S/tt=F/m.
Как связаны эти половинки равенства? Обратите внимание на поиск «а» через F и m .
Задачка: машина m=1165 кг. Мощность мотора= 75 л.с. («Москвич», «Жигули»).
Вопрос: за сколько секунд машина наберёт скорость 100 км/час.
За какое время машина максимально быстро пройдёт 150 м, 250 м., 400 м.
Какую скорость наберёт за 10 сек, за 15 сек., за 25 сек.?
Решение: F/m=a. кпд двс=16%. 75 л.с=5625 кг.м/с 16% будет: 5625/6,25=900 кг.м/сек. Это 12 л.с. (при 100% кпд) a=F/m. 900/1165=0,77 м/сек.сек. Это «ускорение» F/m — «ЭНЕРГИЯ движения»
Скорость 100 км/час (27,7 м/с машина набирает за 18 сек.) a=V средняя/t. 13,9/18=0,77 м/сек.сек. «УСКОРЕНИЕ ОДИНАКОВО и через ЭНЕРГИЮ «at» и через «прибавку скорости к скорости»
-скорость машины через 10 сек.: V кон.=2at. 2*0,77*10=15,4 м/с. 55,5 км/час.
———————————— 15 сек.: 2*0,77*15=23,1 м/с 83,2 км/час.
————————————25 сек.: 2*0,77*25=38,5 м/сек. 138,6 км/ч.
максимальную скорость 153 км/час машины наберут за: 42,5/0,77=55,2 сек.
S=att. 10 c. S=0,77*10*10=77 м
15 с. S=173,25 м
25 с. S=481,25 м
За 55,2 сек. машина проедет: 0,77*55,2*55,2=2346 м.
Обратите внимание: V конечная=2at (a НЕ at); S=att (a НЕ att/2 !)
Вывод: «Ускорение»-это ЭНЕРГИЯ движения (м/сек.сек.) РАВНАЯ ЧИСЛЕННО «прибавке скорости к скорости» S/tt, Vср./t
———: с помощью «а» надо искать F. S,v,t можно измеритью
а что это за ошибка att/2? и Почему это ошибка вы доказали верность теорий энергий , но не ошибочности att/2. Я думаю нужно обьяснить я сам плох в физике поэтому описал как смог.
Тело движется прямолинейно под действием постоянной силы 12 Н, при этом зависимость координаты тела от времени имеет вид: (м). Определить: массу тела; импульс тела в момент времени t = 2 c ; среднюю скорость за промежуток времени от t1 = 0 c до t2 = 2 c.
S/tt=F/m. S=? Тело двигалось,или стояло?
при решении задач на «рав. дв. с начальной скоростью больше (или меньше 0) искать «а» надо со ВСЕГО пути,а не только с момента V о.
…Если машина прошла 100 км. и только один раз ускорилась в течении 10 сек., то это не значит, что она израсходовала бензин только на разгон.
Даже в космосе, в невесомости.она она когда-нибудь остановилась, постепенно СНИЖАЯ скорость. Значит: её движение- НЕ РАВНОмерное.
Если-бы она продолжала двигаться равномерно, её «ускорение»-ЭНЕРГИЯ движения-снизилась бы в t квадрат раз: (а=10 м/сс…а=0,1 м/сс…а=0,0000……м/сек.сек…..) Задачка:
V нач.=10 м/с. «а»=2 м/сек.сек. t=5 сек. S-? «а»=?
Решение: ….(если будем рассматривать «а» только с момента нарастания скорости, то «а» не надо искать. Оно=2 м/сек.сек. А,вот, на ВЕСЬ путь ускорение будет другим: a=S/tt. (без 2S !). h (V конечная) «треугольника»=2at. 2*2*5=20 м/сек. ОБЩАЯ конечная скорость=10+20.
Получилась ТРАПЕЦИЯ, площадь которой-(путь)= (v+v+2at)/2*t. (10+10+20)/2*5. S=100 м. «а»=100/25=4 м/сек.сек. (или считать V ср./t
20/5=4 м/сек.сек.
НЕ ЗАБЫВАЙ-ТЕ и НЕ ПУТАЙ-ТЕ: at- это СРЕДНЯЯ скорость . 2at- это КОНЕЧНАЯ скорость. (при V нач.=0) И ещё: СРЕДНЯЯ скорость и ускорение НЕ зависят от графика движения тела! СРЕДНЯЯ скорость-это «равномерное движение». Скорость at-это то-же РАВНОМЕРНОЕ движение, V нач.=V конечной.. Если нач.и кон. скорости НЕ равны- это НЕ скорость at, и НЕ средняя скорость….
…Ошибка в формуле S=att/2 привела к этой «белеберде», к «интегралам». S/t=at, a at*t=2S (!?). «яблоко…» : 4,9/1=4,9. 4,9/1=9,8 ?!
S,t.m…можно ИЗМЕРИТЬ. Задача-найти F ! S/tt=F/m. Вот таким должен был быть труд Ньютона. НО ошибка «/2….»
….мощность мотора при условиях в задаче. (вес машины…1200 кг)
..машина имела ускорение 4 м/сс.. (для машины-«приличное» ускорение..) F/1200=4 сек.сек. F=4800 кг м./сек. Это=64 л.с. при 100% КПД
КПД ДВС=16 %. 64*6,25=400 л.с. (есть такие моторы. Правда, вес ТАКИХ машин 2,5-3 тонны…) Вот пример «теории и практики». А если вес машины …2650 кг., то мотор должен быть: 4*2650/75*6,25=883 л.с.
Определить тормозную путь,если известны начальная скорость 30 м/сек и замедление 6 м/сек2
V кон.=2at. 30=2*6*t. t=2,5 c. S=att. 6*2,5*2,5. S=37,5 м.
В 1-ой задаче (про самолёт): Vконечная=Vo+2at. V кон.=1008 км/час.
Путь(S)= (Vo+at)*t. (100+9*10)*10. S=1900 м. (если искать по площади трапеции, : (Vo+Vo+2at)/2*t. (200+180)/2*10. S=1900 м.
«а» «общее»= S/tt. 1900/100=19 м/сек.сек. При таком «ускорении» скорость через 30 сек.будет: 19*900=61560 км/ч .
«ускорение» 9 м/сек.сек.-это уже 2 раза превышает ускорение «яблока…». ….а ускорение 19 м/сс в течении 10 сек. (думаю)человек не перенесёт
В последней задаче: t= V ср./ a. Vср.=15 м/с. t=15/6=2,5 секунды (быстрее свободного падения…) S=att. 6*2,5*2/5=37,5 м.
(…напутал в решении…)
При «ускорении» 19 м/сс, скорость через 30 сек. будет: Vкон.=2at. 2*19*30. V кон.=1140 м/с. (4104 км/час)
задача № 11. V o=10. V кон.=12,5. S=600. a=? t=?
Решение: S=(v+V)/2*t. 600=11,25*t. t=53,3..сек. Всё верно ! А.вот, ускорение будет другим: a=S/tt. 600/53,3/53,3=0,21 м/сек.сек.
проверка: S=att. 0,21*53,3*53,3=600. (если S=att/2, то S=300 м. , а «ускорение» -? a=(V-v)/t (?), 2s/tt (?)… a=S/tt, или V средняя/t !
И ещё: почему при решении задач с разными нач.и кон. скоростями вместо трапеции рисуют какие-то «чёрточки со стрелками, и каким-то «ящичком » ? ПЛОЩАДЬ трапеции -это ПУТЬ. S=(V+V)/2*t ! Значения НЕ имеет, какая скорость больше: нач., или конечная : (v+V)/2, или (V+v)2, потому, что ДВИЖЕНИЕ-это ЭНЕРГИЯ*t. «at » at при любом графике движения ЕСТЬ (и равна) СРЕДНЕЙ СКОРОСТИ. Все вычисления надо делать из СРЕДНЕЙ скорости! ( S=at/2*t ? a=(v-V)/t ?)
во второй задаче: V нач.=25 м/с. а=0,1 м/сс. t=60 c. S=? (давать надо одно: или «ускорение», или «время»)
решение: S=V ср.*t. 12,5*60=750 м. «ускорение»= V ср./t. 12,5/60. t=0,2 м/сс.
При «а»=0,1 м/сс. t=Vср./a. 12,5/0,1=125 секунд.
S при а=0,2 м/сс. S=att. 0,208*60*60=750 м. (и при разгоне, и при торможении)
S при а=0,1 м/сс. S=att. 0,1/125*125. S=1562,5 м. (и при разгоне. и при торможении)
задачка: Vo=0. V коечная=0 (как в жизни, на практике). S=100 м. t=5 c. «а»=?
Решение: a=S/tt. 100:25=4 м/сс.
2). Vo=0. V кон.=40. t=5 c. S=100 м. «а»=?
Решение: a=(0+40)/2t. a=4 м/сс.
3). Vo=40. V кон.=0. S=100. t=5. «а»=? Ответ: «а»=4 м/сс
4) Vo=20. V кон.=20. S=100. t=5. «а»=? Решение: а=V СРЕДНЯЯ !/t. (20+20)/2t. a=4 м/сс
Вывод: «ГРАФИК ДВИЖЕНИЯ НЕ влияет на СРЕДНЮЮ СКОРОСТЬ и УСКОРЕНИЕ (если S и t- НЕИЗМЕННЫ!)
задача № 9
V нач.=х. V кон.=5х. V ср.=3х. t=2c. S=18 м. V ср.=9 м. х=9/3=3 м/с. V кон.=15 м/с.
a=S/tt=Vср./t a=18/4=9/2=4,5 м/сс
ПРОВЕРКА: S=att. 4,5*2*2=18 м.
Проверка (по Вашему решению): a=6 м/сс. S=att/2. 6*2*2/2=12 м (?)
У Вас не получается, потому что Вы проверяете ответ по своей формуле. Правильная формула проекции перемещения указана в начале статьи и в самой задаче!
Товарищ Иван, не вводите в заблуждение других людей, если почитали СТО и решили, что в силах пересмотреть законы Ньютона, то для начала почитайте и ОТО и СТО повнимательней, а то от вашего бреда даже глаза слезятся… То, что вы приводите в качестве аргументов — оными не является, т.к доказательной базы кроме придуманных вами расчетов — 0, т.е. нет, т.е. вообще нет, от слова совсем. Плюсом могу добавить, что подобный «контент» не рассматривается на таком уровне (9 класс) , т.к. у детей от чрезмерных уточнений в области физики поедет крыша. Все это больше напоминает поговорку: «Заставь дурака молиться — он себе лоб расшибет». Удачи в научных изысканиях ( с уважением и без сарказма).
Вот такие «анонимы» в средневековье … всех, кто думал не так, как «принято». (текст изменен модератором сайта)
Во второй задаче некорректная формулировка. По факту, даны избыточные данные. «Тормозной путь» соответствует расстоянию до полной остановки, то есть такое понятие подразумевает конечную скорость, равную нулю. А по заданным числам конечная скорость будет равна v0 — a * t = 25 — 0.1*60 = 19 м/c.
Возможно, конкретно в это задаче автор подразумевал под тормозным путём участок, на котором поезд замедлял движение, при этом не до полной остановки. Меня это тоже вначале сбило с толку.
V нач.=25 м/с. t=60 c. V кон.=0. V кон. (от 0 до 25м/с, или ОТ 25 м/с ДО «0»- БЕЗ РАЗНИЦЫ !) V СРЕДНЯЯ (12,5)=at. t=60 c. a=12,5/60=0,2 м/сс
При ТАКОМ изменении скорости S=att. 0,2*60*60=750 м.
При «замедлении» (или наращивании) скорости) =0,1 м/сс S=att. 0,1*60*60=360 м. Но, при а=0,1 м/сс за 60 сек. V кон.=2at. 2*0,1*60=12 м/с
Т.Е.: Если-бы начальная скорость была=12 м/с, ускорение=0,1 м/сс, то через 60 с. поезд прошёл-бы 360 м. и ОСТАНОВИЛСЯ.
До остановки поезда при «замедлении»= 0,1 м/сс со скорости 25 м/с надо: V кон.=2at. 25=2*0,1*t. t=125 сек.
750 м. при замедлении о,1 м/сс tt=750/a. t=86,6 секунды.
Что-бы не было такой «путаницы» НЕ надо давать в условии задачи вместе V,S,t,a .
(Даша! V нач.-это МГНОВЕННАЯ скорость. А скорость at- это СРЕДНЯЯ (постоянная,равномерная) скорость. ТАК нельзя отнимать.
В 11-й задаче проще использовать формулу a = (V-Vo) / t
Даша! V конечная (при равно-ускоренном движении и одной из скоростей=0 ) есть 2at. СРЕДНЯЯ скорость (25+0)/2=12,5 м/с. С такой СРЕДНЕЙ скоростью поезд за минуту (60 сек) пройдёт: 12,5*60=750 м.
Если задачу решать через «а», то t=12,5/0,1=125 секунд. S=V ср.*t. 12,5*125=1562,5 м.
Если поезд (по условию задачи) прошёл 750 м. (до остановки), то его ЗАМЕДЛЕНИЕ скорости (-«а»): S=att 750/60/60. а=0,2 м/сс.
Вывод: давать в условии задачи одно: или «а», или t
Добрый день. Задача №2. Почему ax= -0/1, а не 0,1?
С точки зрения физики торможение — это тоже ускорение, только с обратным знаком. Поменяли условие задачи № 2, чтобы не было двусмысленности.
всем доброго времени.
Очень е силен в физике последние лет 25, по этой причине прошу помочь в решении некой задачи!
Дано начальная скорость = 10 м/с.
Вопрос сможет ли тело долететь до высоты 4 м и если сможет то с какой скоростью. Да, полет вертикальный!
На мой взгляд в даны не все условия, но могу и ошибаться.
Спасибо.
Такие задачи рассматриваются в разделе «Задачи на свободное падение» https://uchitel.pro/задачи-на-свободное-падение/
Добавить комментарий Отменить ответ
Конспекты по физике:
7 класс
- Физические величины
- Строение вещества
- Механическое движение. Траектория
- Прямолинейное равномерное движение
- Неравномерное движение. Средняя скорость
- ЗАДАЧИ на движение с решением
- Масса тела. Плотность вещества
- ЗАДАЧИ на плотность, массу и объем
- Силы вокруг нас (силы тяжести, трения, упругости)
- ЗАДАЧИ на силу тяжести и вес тела
- Давление тел, жидкостей и газов
- ЗАДАЧИ на давление твердых тел с решениями
- ЗАДАЧИ на давление жидкостей с решениями
- Закон Архимеда
- Сообщающиеся сосуды. Шлюзы
- ЗАДАЧИ на силу Архимеда с решениями
- Механическая работа, мощность и КПД
- ЗАДАЧИ на механическую работу с решениями
- ЗАДАЧИ на механическую мощность
- Простые механизмы. Блоки
- Рычаг. Равновесие рычага. Момент силы
- ЗАДАЧИ на простые механизмы с решениями
- ЗАДАЧИ на КПД простых механизмов
- Механическая энергия. Закон сохранения энергии
- Физика 7: все формулы и определения
- ЗАДАЧИ на Сообщающиеся сосуды
- ЗАДАЧИ на силу упругости с решениями
8 класс
- Введение в оптику
- Тепловое движение. Броуновское движение
- Диффузия. Взаимодействие молекул
- Тепловое равновесие. Температура. Шкала Цельсия
- Внутренняя энергия
- Виды теплопередачи: теплопроводность, конвекция, излучение
- Количество теплоты. Удельная теплоёмкость
- Уравнение теплового баланса
- Испарение. Конденсация
- Кипение. Удельная теплота парообразования
- Влажность воздуха
- Плавление и кристаллизация
- Тепловые машины. ДВС. Удельная теплота сгорания топлива
- Электризация тел
- Два вида электрических зарядов. Взаимодействие зарядов
- Закон сохранения электрического заряда
- Электрическое поле. Проводники и диэлектрики
- Постоянный электрический ток
- Сила тока. Напряжение
- Электрическое сопротивление
- Закон Ома. Соединение проводников
- Работа и мощность электрического тока
- Закон Джоуля-Ленца и его применение
- Электромагнитные явления
- Колебательные и волновые явления
- Физика 8: все формулы и определения
- ЗАДАЧИ на количество теплоты с решениями
- ЗАДАЧИ на сгорание топлива с решениями
- ЗАДАЧИ на плавление и отвердевание
- ЗАДАЧИ на парообразование и конденсацию
- ЗАДАЧИ на КПД тепловых двигателей
- ЗАДАЧИ на Закон Ома с решениями
- ЗАДАЧИ на сопротивление проводников
- ЗАДАЧИ на Последовательное соединение
- ЗАДАЧИ на Параллельное соединение
- ЗАДАЧИ на Работу электрического тока
- ЗАДАЧИ на Мощность электрического тока
- ЗАДАЧИ на Закон Джоуля-Ленца
- Опыты Эрстеда. Магнитное поле. Электромагнит
- Магнитное поле постоянного магнита
- Действие магнитного поля на проводник с током
- Электромагнитная индукция. Опыты Фарадея
- Явления распространения света
- Дисперсия света. Линза
- Оптические приборы
- Электромагнитные колебания и волны
9 класс
- Введение в квантовую физику
- Формула времени. Решение задач
- ЗАДАЧИ на Прямолинейное равномерное движение
- ЗАДАЧИ на Прямолинейное равноускоренное движение
- ЗАДАЧИ на Свободное падение с решениями
- ЗАДАЧИ на Законы Ньютона с решениями
- ЗАДАЧИ закон всемирного тяготения
- ЗАДАЧИ на Движение тела по окружности
- ЗАДАЧИ на искусственные спутники Земли
- ЗАДАЧИ на Закон сохранения импульса
- ЗАДАЧИ на Механические колебания
- ЗАДАЧИ на Механические волны
- ЗАДАЧИ на Состав атома и ядерные реакции
- ЗАДАЧИ на Электромагнитные волны
- Физика 9 класс. Все формулы и определения
- Относительность движения
- Равномерное прямолинейное движение
- Прямолинейное равноускоренное движение
- Свободное падение
- Скорость равномерного движения тела по окружности
- Масса. Плотность вещества
- Сила – векторная физическая величина
- Первый закон Ньютона
- Второй закон Ньютона. Третий закон Ньютона
- Трение покоя и трение скольжения
- Деформация тела
- Всемирное тяготение. Сила тяжести
- Импульс тела. Закон сохранения импульса
- Механическая работа. Механическая мощность
- Кинетическая и потенциальная энергия
- Механическая энергия
- Золотое правило механики
- Давление твёрдого тела. Давление газа
- Закон Паскаля. Гидравлический пресс
- Закон Архимеда. Условие плавания тел
- Механические колебания и волны. Звук
- МКТ. Агрегатные состояния вещества
- Радиоактивность. Излучения. Распад
- Опыты Резерфорда. Планетарная модель атома
- Состав атомного ядра. Изотопы
- Ядерные реакции. Ядерный реактор
- ЗАДАЧИ на Движение под действием нескольких сил
- ЗАДАЧИ на Движение под действием силы трения
10-11 классы
- Молекулярно-кинетическая теория
- Кинематика. Теория и формулы + Шпаргалка
- Динамика. Теория и формулы + Шпаргалка
- Законы сохранения. Работа и мощность. Теория, Формулы, Шпаргалка
- Статика и гидростатика. Теория и формулы + Шпаргалка
- Термодинамика. Теория, формулы, схемы
- Электростатика. Теория и формулы + Шпаргалка
- Постоянный ток. Теория, формулы, схемы
- Магнитное поле. Теория, формулы, схемы
- Электромагнитная индукция
- Закон сохранения импульса. Задачи ЕГЭ с решениями
- Колебания и волны Задачи ЕГЭ с решениями
- Физика 10 класс. Все формулы и темы
- Физика 11 класс. Все формулы и определения
- Световые кванты
- ЕГЭ Квантовая физика. Задачи с решениями
- Излучения и спектры
- Атомная физика (физика атома)
- ЕГЭ Закон Кулона. ЗАДАЧИ с решениями
- Электрическое поле. ЗАДАЧИ с решениями
- Потенциал. Разность потенциалов. ЗАДАЧИ с решениями
- Закон Ома. Соединение проводников. ЗАДАЧИ на ЕГЭ
- Закон Ома для всей цепи. ЗАДАЧИ на ЕГЭ
- ЗАДАЧИ на Колебания и волны (с решениями)
- Электромагнитные колебания
Найти конспект:
О проекте
Сайт «УчительPRO» — некоммерческий школьный проект учеников, их родителей и учителей. Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie и других пользовательских данных в целях функционирования сайта, проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.
Возрастная категория: 12+
(с) 2021 Учитель.PRO — Копирование информации с сайта только при указании активной ссылки на сайт!
💡 Видео
Решение графических задач на равномерное движениеСкачать

Скорость прямолинейного равноускоренного движения. График скорости | Физика 9 класс #6 | ИнфоурокСкачать

Графики зависимости пути и скорости от времениСкачать

Физика-9. "График проекции скорости"Скачать

ЕГЭ по физике. Задание 1. Определение пройденного пути по графику скоростиСкачать
Физика перемещение, скорость и ускорение График движения 2016Скачать

Прямолинейное равноускоренное движение. Ускорение | Физика 9 класс #5 | ИнфоурокСкачать

Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

Задача из ЕГЭ по физике │Анализ графика #1Скачать

Физика - уравнения равноускоренного движенияСкачать

Как найти проекцию вектора скорости и ускорения. Выполнялка 112Скачать

7 класс, 6 урок, Графики зависимости пути и скорости от времениСкачать

Как определить путь по графику скоростиСкачать

Графики зависимости кинематических величин от времени при равномерном и равноускоренном движенииСкачать

Физика 7 класс (Урок№8 - Скорость.)Скачать

Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать