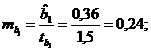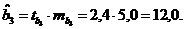По 30 наблюдениям было оценено следующее уравнение регрессии (4 видео)

Типовая задача 1 По 30 предприятиям отрасли были получены следующие результаты регрессионного анализа зависимости объема выпуска продукции у (млн. руб.) от численности занятых на предприятии х1(чел.) и среднегодовой стоимости основных фондов х2(млн. руб.) (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6

Типовая задача 1

По 30 предприятиям отрасли были получены следующие результаты регрессионного анализа зависимости объема выпуска продукции у (млн. руб.) от численности занятых на предприятии х1(чел.) и среднегодовой стоимости основных фондов х2(млн. руб.).

Множественный коэффициент корреляции

Стандартные ошибки параметров

t-критерий для параметров

1. Восстановите пропущенные характеристики.

2. С вероятностью 0,95 постройте доверительные интервалы для коэффициентов регрессии.

3.Проанализируйте результаты регрессионного анализа.

Множественный коэффициент корреляции

Стандартные ошибки параметров

t-критерий для параметров

2) ; а=2*1,5=3;

4) ; mb2=20/4=5

2. Границы доверительного интервала определяются по формуле: ;

tтабл определяется для принятого уровня значимости б=0,05 (так как по условию заданный уровень вероятности составляет 0,95) и числа степеней свободы df=n-m-1=30-2-1=27

Границы доверительного интервала для параметра b1:

Границы доверительного интервала для параметра b2:

20 -5*2,052≤ b2≤20+5*2,052

Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 0,95 параметры a, b1, b2 , не являются статистически незначимыми и существенно отличны от нуля.

3. Проверим надежность результатов регрессионного анализа:

Fфакт >Fтабл. Уравнение регрессии в целом статистически значимо.

Коэффициенты b1 и b2 являются статистически значимыми, так как для b1 tфакт=8>2,052=tтабл, а для b2 tфакт=4>2,052.

Типовая задача 2

Производственная функция, полученная по данным за 1990-1997гг, характеризуется уравнением

R2=0,9843, r2PZ=0,7826, r2PK=0,9836

Где: Р-индекс промышленного производства, Z-численность рабочих, К-капитал.

В скобках указаны значения стандартных ошибок для коэффициентов регрессии.

Дайте интерпретацию параметров уравнения регрессии. Оцените значимость параметров регрессии с помощью t-критерия Стъюдента и сделайте вывод о целесообразности включения факторов в модель. Оцените значимость уравнения регрессии в целом с помощью F-критерия Фишера. Найдите величины частных значений F-критерия и сделайте соответствующие выводы. Какова роль факторов, неучтенных в модели, в вариации индекса промышленного производства.

Пункты 1-3 выполнить самостоятельно.

4.Величины частных значений F-критерия составляют:

F1 Fтабл. Гипотеза Н0 о несущественности прироста коэффициента детерминации за счет включения капитала отклоняется, приходим к выводу о статистически подтвержденной целесообразности включения в модель фактора К.

5. Роль факторов, неучтенных в модели, в вариации индекса промышленного производства составляет

1-R2 = 1-0,9843=0,0157 (1,57% )

Типовая задача 3

По 30 наблюдениям получены следующие данные :

1. Найдите скорректированный коэффициент корреляции, оцените значимость уравнения регрессии в целом.

2. Определите частные коэффициенты эластичности.

3.Оцените параметр а.

1. Скорректированный коэффициент детерминации составит:

Скорректированный коэффициент корреляции составит .

2. Частные коэффициенты эластичности:

Сделать выводы по рассчитанным значениям.

3. Значение параметра а составит:

=200-0,176*150-0,014*20+7,75*100=948,32

Типовая задача 4

Зависимость потребления электроэнергии у(тыс. кВт*ч) от объемов производства продукции А-х1(тыс. ед) и продукции Б –х2(тыс. ед.) характеризуется следующим образом:

Уравнение регрессии в стандартизованном виде:

1. Сделайте выводы о силе влияния факторов на результат.

2. Учитывая значения коэффициентов вариации рассматриваемых признаков, определите частные коэффициенты эластичности, сделайте по ним выводы.

3.Оцените значимость уравнения регрессии, учитывая, что оно построено по 30 наблюдениям.

1. Фактор х1 сильнее влияет, чем фактор х2, так как в1=0,79> в2=0,56

2.Рассчитаем частные коэффициенты эластичности, зная коэффициенты вариации. Так как

(1)

(2)

Подставляя выражение (2) в формулу (1), получим:

Сделать выводы по полученным значениям.

3. Самостоятельно оценить значимость уравнения регрессии, учитывая, что оно построено по 30 наблюдениям.

По 26 предприятиям отрасли были получены следующие результаты регрессионного анализа зависимости объема выпуска продукции у (млн. руб.) от энерговооруженности труда х1(тыс. кВт. ч/чел.) и численности работников х2(чел.)

Содержание

По 30 наблюдениям матрица парных коэффициентов корреляции оказалась следующей: y x1 x2 x3 y 1,00 x1 0,30 1,00 x2 0,60 0,10 1,00 х3 0,40 0,15 0,80 1,00 Задание 1. Постройте уравнение регрессии
Описание и исходные данные задания, 50% решения + фотография:
Примеры решения задач по множественной регрессии
🔍 Видео

Видео:Множественная степенная регрессияСкачать

По 30 наблюдениям матрица парных коэффициентов корреляции оказалась следующей: y x1 x2 x3 y 1,00 x1 0,30 1,00 x2 0,60 0,10 1,00 х3 0,40 0,15 0,80 1,00 Задание 1. Постройте уравнение регрессии

Готовое решение: Заказ №9412

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Экономика

Дата выполнения: 19.10.2020

Цена: 229 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

По 30 наблюдениям матрица парных коэффициентов корреляции оказалась следующей:

Постройте уравнение регрессии в стандартизованном виде и сделайте выводы.
Определите показатель множественной корреляции (нескорректированный и скорректированный).
Оцените целесообразность включения переменной x₁ в модель после введения в нее переменных x₂ и x₃ .

Решение:

1) Среди полученных коэффициентов парной корреляции между факторными признаками есть превышающие 0,7 по модулю, т.е. присутствует мультиколлинеарность в исходных данных.

В анализ целесообразно включить фактор Х₂, а не Х₃, т.к. корреляция 2 Х₃ с результатом слабее, чем корреляция фактора Х₂ с У. Поэтому в данном случае в уравнение множественной регрессии включаются факторы Х₁ и Х₂.

2) На основе построенной матрицы коэффициентов корреляции составляется и решается относительно система уравнений:

r yx 1 = β 1 + β 2 r x 2 x 1 + β 3 r x 3 x 1 +…+ β p r xpx 1 r yx 2 = β 1 r x 2 x 1 + β 2 + β 3 r x 3 x 2 +…+ β p r xpx 2 ….=…+…+….+…+….. r yxp = β 1 r xpx 1 + β 2 r xpx 2 + β 3 r xpx 3 +…..+ β p

0,3= β 1 +0,1 β 2 0,6= 0,1β 1 + β 2

Если вам нужно решить экономику, тогда нажмите ➔ заказать контрольную работу по экономике.

Похожие готовые решения:

По 10 районам РФ имеются данный о средней заработной плате (х, тыс. руб.) и прожиточном минимуме на душу населения (у, тыс. руб./месяц): х 0,52 0,57 0,69 0,77 0,90 0,97 1,04 1,08 1,49 1,63 у 0,28 0,33
В таблице представлены результаты наблюдений за х1, х2 и у: х1 1 9 4 1 5 1 2 4 1 3 Х2 9 6 8 2 4 3 7 2 5 2 у 6 1 9 3 2 7 1 4 3 9 1) Найти МНК-оценки параметров уравнения
Численность населения города составляла в 2000 г.: по состоянию на 1 января — 1238 тыс. чел.; на 1 марта — 1240 тыс. чел.; на 1 июня — 1350 тыс. чел.
Численность населения области на 1 января 2000 г. составляла 4836 тыс. чел., на 1 апреля — 4800 тыс. чел., на 1 июля — 4905 тыс. чел., на 1 октября — 4890 тыс. чел.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Примеры решения задач по множественной регрессии

Пример 1. Уравнение регрессии, построенное по 17 наблюдениям, имеет вид:

Расставить пропущенные значения, а также построить доверительный интервал для b₂ с вероятностью 0,99.

Решение. Пропущенные значения определяем с помощью формул:

Таким образом, уравнение регрессии со статистическими характеристиками выглядит так:

Доверительный интервал для b₂ строим по соответствующей формуле. Здесь уровень значимости равен 0,01, а число степеней свободы равно n – p – 1 = 17 – 3 – 1 = 13, где n = 17 – объём выборки, p = 3 – число факторов в уравнении регрессии. Отсюда

или . Этот доверительный интервал накрывает истинное значение параметра с вероятностью, равной 0,99.

Пример 2.Уравнение регрессии в стандартизованных переменных выглядит так:

При этом вариации всех переменных равны следующим величинам:

Сравнить факторы по степени влияния на результирующий признак и определить значения частных коэффициентов эластичности.

Решение.Стандартизованные уравнения регрессии позволяют сравнивать факторы по силе их влияния на результат. При этом, чем больше по абсолютной величине коэффициент при стандартизованной переменной, тем сильнее данный фактор влияет на результирующий признак. В рассматриваемом уравнении самое сильное воздействие на результат оказывает фактор х₁, имеющий коэффициент – 0,82, самое слабое – фактор х₃ с коэффициентом, равным – 0,43.

В линейной модели множественной регрессии обобщающий (средний) коэффициент частной эластичности определяется выражением, в которое входят средние значения переменных и коэффициент при соответствующем факторе уравнения регрессии натурального масштаба. В условиях задачи эти величины не заданы. Поэтому воспользуемся выражениями для вариации по переменным:

Коэффициенты b_j связаны со стандартизованными коэффициентами β_j соответствующим соотношением, которое подставим в формулу для среднего коэффициента эластичности:

При этом знак коэффициента эластичности будет совпадать со знаком β_j:

Пример 3. По 32 наблюдениям получены следующие данные:

Определить значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра а.

Решение. Значение скорректированного коэффициента детерминации определим по одному из формул для его вычисления:

Частные коэффициенты эластичности (средние по совокупности) вычисляем по соответствующим формулам:

Поскольку линейное уравнение множественной регрессии выполняется при подстановке в него средних значений всех переменных, определяем параметр а:

Пример 4. По некоторым переменным имеются следующие статистические данные:

Построить уравнение регрессии в стандартизованном и натуральном масштабах.

Решение.Поскольку изначально известны коэффициенты парной корреляции между переменными, начать следует с построения уравнения регрессии в стандартизованном масштабе. Для этого надо решить соответствующую систему нормальных уравнений, которая в случае двух факторов имеет вид:

или, после подстановки исходных данных:

Решаем эту систему любым способом, получаем: β₁ = 0,3076, β₂ = 0,62.

Запишем уравнение регрессии в стандартизованном масштабе:

Теперь перейдем к уравнению регрессии в натуральном масштабе, для чего используем формулы расчета коэффициентов регрессии через бета-коэффициенты и свойство справедливости уравнения регрессии для средних переменных:

Уравнение регрессии в натуральном масштабе имеет вид:

Пример 5.При построении линейной множественной регрессии по 48 измерениям коэффициент детерминации составил 0,578. После исключения факторов х₃, х₇ и х₈ коэффициент детерминации уменьшился до 0,495. Обоснованно ли было принятое решение об изменении состава влияющих переменных на уровнях значимости 0,1, 0,05 и 0,01?

Решение.Пусть — коэффициент детерминации уравнения регрессии при первоначальном наборе факторов, — коэффициент детерминации после исключения трех факторов. Выдвигаем гипотезы:

;

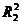
Основная гипотеза предполагает, что уменьшение величины было несущественным, и решение об исключении группы факторов было правильным. Альтернативная гипотеза говорит о правильности принятого решения об исключении.

Для проверки нуль – гипотезы используем следующую статистику:

где n = 48, p = 10 – первоначальное количество факторов, k = 3 – количество исключаемых факторов. Тогда

Сравним полученное значение с критическим F(α; 3; 39) на уровнях 0,1; 0,05 и 0,01:

На уровне α = 0,1 F_набл > F_кр, нуль – гипотеза отвергается, исключение данной группы факторов не оправдано, на уровнях 0,05 0,01 нуль – гипотеза не может быть отвергнута, и исключение факторов можно считать оправданным.

Пример 6. На основе квартальных данных с 2000 г. по 2004 г. получено уравнение . При этом ESS=110,3, RSS=21,4 (ESS – объясненная СКО, RSS – остаточная СКО). В уравнение были добавлены три фиктивные переменные, соответствующие трем первым кварталам года, и величина ESS увеличилась до 120,2. Присутствует ли сезонность в этом уравнении?

Решение. Это задача на проверку обоснованности включения группы факторов в уравнение множественной регрессии. В первоначальное уравнение с тремя факторами были добавлены три переменные, соответствующие первым трем кварталам года.

Определим коэффициенты детерминации уравнений. Общая СКО определяется как сумма факторной и остаточной СКО:

ТSS = ESS₁ + RSS₁ = 110,3 + 21,4 = 131,7

Проверяем гипотезы . Для проверки нуль – гипотезы используем статистику

Здесь n = 20 (20 кварталов за пять лет – с 2000 г. по 2004 г.), p = 6 (общее количество факторов в уравнении регрессии после включения новых факторов), k = 3 (количество включаемых факторов). Таким образом:

Определим критические значения статистики Фишера на различных уровнях значимости:

На уровнях значимости 0,1 и 0,05 F_набл> F_кр, нуль – гипотеза отвергается в пользу альтернативной, и учет сезонности в регрессии является обоснованным (добавление трех новых факторов оправдано), а на уровне 0,01 F_набл F_кр, и гетероскедастичность имеет место, а на уровне 0,01 F_набл .