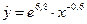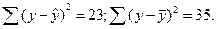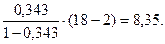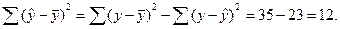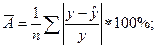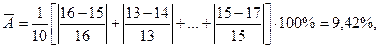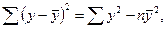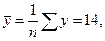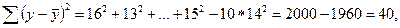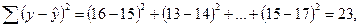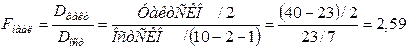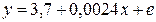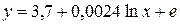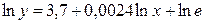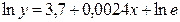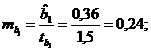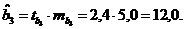Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии
В сервисе для нахождения параметров регрессии используется МНК. Система нормальных уравнений для линейной регрессии: 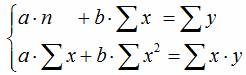
Уравнение парной регрессии относится к уравнению регрессии первого порядка. Если эконометрическая модель содержит только одну объясняющую переменную, то она имеет название парной регрессии. Уравнение регрессии второго порядка и уравнение регрессии третьего порядка относятся к нелинейным уравнениям регрессии.
Пример . Осуществите выбор зависимой (объясняемой) и объясняющей переменной для построения парной регрессионной модели. Дайте графическое изображение регрессионной зависимости. Определите теоретическое уравнение парной регрессии. Оцените адекватность построенной модели (интерпретируйте R-квадрат, показатели t-статистики, F-статистики).
Решение будем проводить на основе процесса эконометрического моделирования.
1-й этап (постановочный) – определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли.
Спецификация модели — определение цели исследования и выбор экономических переменных модели.
Ситуационная (практическая) задача. По 10 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x (в %).
2-й этап (априорный) – предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез.
Уже на этом этапе можно говорить о явной зависимости уровня квалификации рабочего и его выработкой, ведь чем опытней работник, тем выше его производительность. Но как эту зависимость оценить?
Парная регрессия представляет собой регрессию между двумя переменными – y и x , т. е. модель вида:
Видео:Множественная регрессия в ExcelСкачать

Примеры решения задач по парной регрессии
Задача 1.Исследуя спрос на продукцию фирмы, аналитический отдел собрал данные по 20 торговым точкам компании и представил их в виде:
ln y = 6,8 – 0,6 ln x + ε,
где y – объем спроса,
x – цена единицы продукции.
В скобках приведены фактически значения t – критерия.
Ранее предполагалось, что увеличение цены на 1% приводит к уменьшению спроса на 1,2%. Можно ли утверждать, что приведенные результаты подтверждают это предположение?
Уравнение регрессии в прологарифмированном виде. Судя по форме записи, уравнение имеет степенной вид и записывается так:
Надо проверить предположение о том, что эластичность спроса по цене равна –1,2. В степенной зависимости эластичность равна показателю степени b , поэтому оценка эластичности равна –0,6. Таким образом, задача сводится к проверке статистической гипотезы (нуль — гипотезы) H0:b=-1,2 против альтернативной H1:b≠-1,2. Критическая область двусторонняя, поэтому проверка гипотезы может быть заменена построением доверительного интервала для b и, если проверяемое значение b=-1,2 попадает в него, то нуль-гипотеза не отклоняется; в противном случае принимается альтернативная гипотеза.
Интервал строится по формуле (23):
Можно проверить статистическую гипотезу напрямую, вычислив t –статистику для разницы между гипотетическим и вычисленным значениями b:
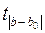
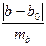
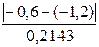
Сравним полученную статистику по абсолютной величине с критическим значением на заданном уровне значимости. На уровне α=0,05:
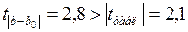
Нуль-гипотеза отклоняется, эластичность спроса по цене не может быть равна –1,2. На уровне α=0,01:
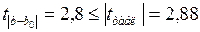
нуль-гипотеза не отклоняется, эластичность может быть равна –1,2.
Задача 2.Для двух видов продукции А и Б зависимости удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:
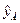
Сравнить эластичность затрат по каждому виду продукции при x=50 и определить объемы продукции обоих видов, при котором эластичности будут одинаковы.
РешениеРегрессионная зависимость для продукции А является полулогарифмической, и для вычисления эластичности воспользуемся формулой:
ЭА = 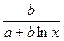
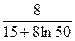
Для продукции Б регрессионная зависимость является степенной, где коэффициент эластичности равен показателю степени при любых значениях независимой переменной, следовательно:
Теперь определим точку, в которой эластичности по обоим видам продукции одинаковы. Для продукции Б подходит любой объем, т.к. эластичность постоянна, а для определения объема выпуска продукции А составим и решим уравнение:
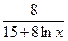
Таким образом, при объеме производства продукции А, равном 4,3, эластичности удельных постоянных расходов обоих видов продукции по объему выпуска одинаковы и равны 0,3.
Задача 3.Пусть имеется уравнение парной регрессии: y = 5 — 6x + ε, построенное по 15 наблюдениям. При этом r = –0,7.
Определить доверительный интервал, в который с вероятностью 0,99 попадает коэффициент регрессии.
Решение:Для построения доверительного интервала необходимо знать стандартную ошибку mb коэффициента регрессии. Однако она не задана, и нужно определить ее косвенным путем. Для этого воспользуемся тем, что в парной регрессии существует связь между t- и F-статистиками:
tb = 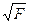
а F — статистику определим из формулы (19):
F = 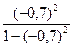
tb = 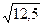
(берем минус, так как знак оцененного коэффициента b отрицательный).
mb = 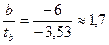
Доверительный интервал имеет вид (tтабл(0,01;13)=3,01):
Далее воспользуемся уравнением (19), из которого определим коэффициент детерминации при n=15:
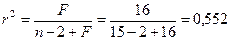
Задача 5.По совокупности 18 предприятий торговли изучается зависимость между ценой x на некоторый товар и прибылью y торгового предприятия. При оценке регрессионной модели были получены следующие результаты:
Определить индекс корреляции и фактическое значение F-критерия, а также статистическую значимость уравнения регрессии. Построить таблицу дисперсионного анализа.
Решение: В условиях задачи n=18; остаточная СКО равна 23, а общая СКО – 35. Для расчета индекса корреляции воспользуемся выражением (54):
R = 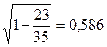
Фактическое значение F-критерия рассчитаем с помощью выражения (19):
F =
При проверке статистической значимости уравнения в целом воспользуемся F-критерием и сравним его с критическим значением, задавшись уровнем значимости 0,05. Табличное (критическое) значение при этом равно:
Поскольку фактическое значение, равное 8,35, больше критического, нуль-гипотезу о статистической незначимости уравнения регрессии следует отклонить, и уравнение на уровне α=0,05 является значимым; статистическая связь между y и x считается доказанной. Однако, если задать α=0,01, то:
и в этом случае нуль-гипотезу отклонить нельзя, на уровне α=0,01 уравнение не значимо.
Для построения таблицы дисперсионного анализа определим из балансового уравнения (13) величину факторной СКО:
Поскольку мы имеем дело с парной регрессионной зависимостью, число степеней свободы факторной СКО принимаем равным единице. С учетом этих условий таблица дисперсионного анализа выглядит следующим образом:
| Вариация y | СКО | Число степеней свободы | Дисперсия на 1 степень свободы | Fнабл= 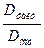 |
| Общая | — | — | ||
| Факторная | 8,35 | |||
| Остаточная | 1,4375 |
Задача 6.Зависимость среднемесячной производительности труда от возраста рабочих характеризуется моделью:
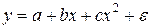
Ее использование привело к результатам, представленным в таблице:
| № п/п | Производительность труда рабочих, тыс.руб. (y) | № п/п | Производительность труда рабочих, тыс. руб. (y) |
| фактическая | расчетная | фактическая | расчетная |
Оценить качество модели, определив ошибку аппроксимации, индекс корреляции и F-критерий Фишера.
Решение: Средняя ошибка аппроксимации рассчитывается по формуле:
и характеризует среднее отклонение расчетных значений от фактических. Это значение считается приемлемым, если оно не превышает 8-10%.
Для приведенных в таблице данных имеем:
что оказывается в допустимых границах и говорит о приемлемой точности аппроксимации регрессионной модели.
Индекс корреляции рассчитаем по формуле (54), предварительно определив общую и остаточную СКО.
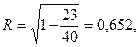
F-критерий рассчитаем по формуле (55) с учетом того, что число параметров при переменной x равно двум (зависимость квадратическая, эти параметры – b и c):
Сравним это значение с критическим на уровне 0,05:
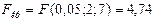
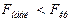
следовательно, уравнение в целом на уровне 0,05 не значимо. Можно предположить, что в исследованном диапазоне строить квадратическую регрессию нецелесообразно. По – видимому, есть смысл упростить уравнение регрессии и описать исходные данные с помощью линейной зависимости.
Задача 7. Для следующих уравнений регрессии:
а)
б)
в)
г)
определить коэффициенты эластичности при значении фактора, равном 85.
а) Уравнение регрессии является линейным, поэтому коэффициент эластичности равен 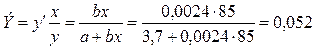
б) Здесь имеем дело с полулогарифмической зависимостью: 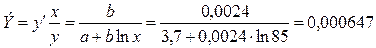
в) Это преобразованная (путем логарифмирования) степенная зависимость; её коэффициент эластичности постоянен и равен показателю степени, т.е. 0,0024.
г) В данном случае зависимость показательная (или экспоненциальная), в преобразованном виде логарифмируется только зависимая переменная. В любой из трех форм записи экспоненциальной регрессии коэффициент эластичности равен произведению коэффициента при факторе на значение самого фактора, т.е. 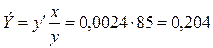
Видео:Эконометрика. Линейная парная регрессияСкачать

Примеры решения задач по множественной регрессии
Пример 1. Уравнение регрессии, построенное по 17 наблюдениям, имеет вид:
Расставить пропущенные значения, а также построить доверительный интервал для b2 с вероятностью 0,99.
Решение. Пропущенные значения определяем с помощью формул:

Таким образом, уравнение регрессии со статистическими характеристиками выглядит так:
Доверительный интервал для b2 строим по соответствующей формуле. Здесь уровень значимости равен 0,01, а число степеней свободы равно n – p – 1 = 17 – 3 – 1 = 13, где n = 17 – объём выборки, p = 3 – число факторов в уравнении регрессии. Отсюда

или 

Пример 2.Уравнение регрессии в стандартизованных переменных выглядит так:

При этом вариации всех переменных равны следующим величинам:

Сравнить факторы по степени влияния на результирующий признак и определить значения частных коэффициентов эластичности.
Решение.Стандартизованные уравнения регрессии позволяют сравнивать факторы по силе их влияния на результат. При этом, чем больше по абсолютной величине коэффициент при стандартизованной переменной, тем сильнее данный фактор влияет на результирующий признак. В рассматриваемом уравнении самое сильное воздействие на результат оказывает фактор х1, имеющий коэффициент – 0,82, самое слабое – фактор х3 с коэффициентом, равным – 0,43.
В линейной модели множественной регрессии обобщающий (средний) коэффициент частной эластичности определяется выражением, в которое входят средние значения переменных и коэффициент при соответствующем факторе уравнения регрессии натурального масштаба. В условиях задачи эти величины не заданы. Поэтому воспользуемся выражениями для вариации по переменным:
Коэффициенты bj связаны со стандартизованными коэффициентами βj соответствующим соотношением, которое подставим в формулу для среднего коэффициента эластичности:

При этом знак коэффициента эластичности будет совпадать со знаком βj:
Пример 3. По 32 наблюдениям получены следующие данные:
Определить значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра а.
Решение. Значение скорректированного коэффициента детерминации определим по одному из формул для его вычисления:
Частные коэффициенты эластичности (средние по совокупности) вычисляем по соответствующим формулам:
Поскольку линейное уравнение множественной регрессии выполняется при подстановке в него средних значений всех переменных, определяем параметр а:
Пример 4. По некоторым переменным имеются следующие статистические данные:





Построить уравнение регрессии в стандартизованном и натуральном масштабах.
Решение.Поскольку изначально известны коэффициенты парной корреляции между переменными, начать следует с построения уравнения регрессии в стандартизованном масштабе. Для этого надо решить соответствующую систему нормальных уравнений, которая в случае двух факторов имеет вид:
или, после подстановки исходных данных:
Решаем эту систему любым способом, получаем: β1 = 0,3076, β2 = 0,62.
Запишем уравнение регрессии в стандартизованном масштабе:
Теперь перейдем к уравнению регрессии в натуральном масштабе, для чего используем формулы расчета коэффициентов регрессии через бета-коэффициенты и свойство справедливости уравнения регрессии для средних переменных:
Уравнение регрессии в натуральном масштабе имеет вид:
Пример 5.При построении линейной множественной регрессии 
Решение.Пусть 

Основная гипотеза предполагает, что уменьшение величины 
Для проверки нуль – гипотезы используем следующую статистику:

где n = 48, p = 10 – первоначальное количество факторов, k = 3 – количество исключаемых факторов. Тогда
Сравним полученное значение с критическим F(α; 3; 39) на уровнях 0,1; 0,05 и 0,01:
На уровне α = 0,1 Fнабл > Fкр, нуль – гипотеза отвергается, исключение данной группы факторов не оправдано, на уровнях 0,05 0,01 нуль – гипотеза не может быть отвергнута, и исключение факторов можно считать оправданным.
Пример 6. На основе квартальных данных с 2000 г. по 2004 г. получено уравнение 
Решение. Это задача на проверку обоснованности включения группы факторов в уравнение множественной регрессии. В первоначальное уравнение с тремя факторами были добавлены три переменные, соответствующие первым трем кварталам года.
Определим коэффициенты детерминации уравнений. Общая СКО определяется как сумма факторной и остаточной СКО:
ТSS = ESS1 + RSS1 = 110,3 + 21,4 = 131,7
Проверяем гипотезы 
Здесь n = 20 (20 кварталов за пять лет – с 2000 г. по 2004 г.), p = 6 (общее количество факторов в уравнении регрессии после включения новых факторов), k = 3 (количество включаемых факторов). Таким образом:
Определим критические значения статистики Фишера на различных уровнях значимости:
На уровнях значимости 0,1 и 0,05 Fнабл> Fкр, нуль – гипотеза отвергается в пользу альтернативной, и учет сезонности в регрессии является обоснованным (добавление трех новых факторов оправдано), а на уровне 0,01 Fнабл Fкр, и гетероскедастичность имеет место, а на уровне 0,01 Fнабл
📽️ Видео
Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

Множественная регрессияСкачать

Множественная регрессия в Excel и мультиколлинеарностьСкачать

Эконометрика. Построение модели множественной регрессии в Excel. Часть 1.Скачать

Парная регрессия: линейная зависимостьСкачать

Построение уравнения линейной регрессии методом наименьших квадратов.Скачать

Уравнение парной линейной регрессии с помощью Анализа ДанныхСкачать

Эконометрика. Множественная регрессия и корреляция.Скачать

Коэффициент линейной регрессии, 2 способаСкачать

Регрессия в ExcelСкачать

Что такое линейная регрессия? Душкин объяснитСкачать

Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Парная нелинейная регрессияСкачать

Множественная регрессия в программе SPSS (Multiple regression)Скачать

Эконометрика Линейная регрессия и корреляцияСкачать

Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Уравнение регрессииСкачать