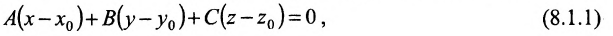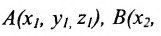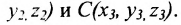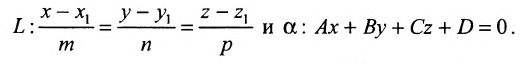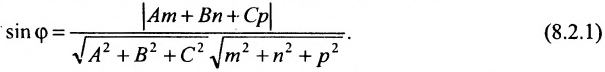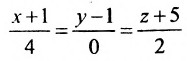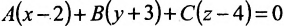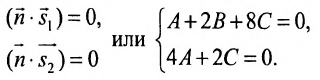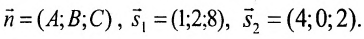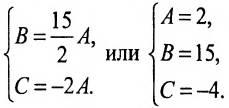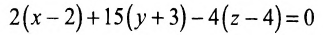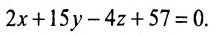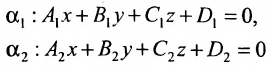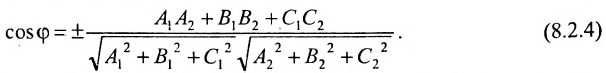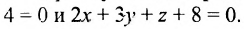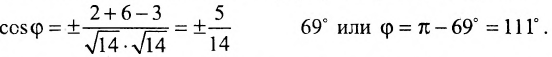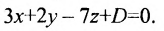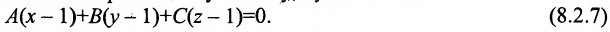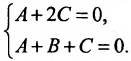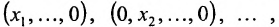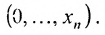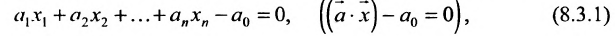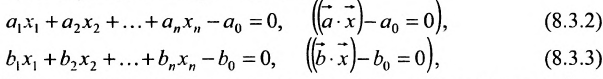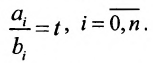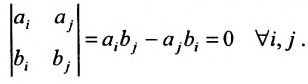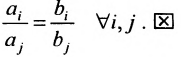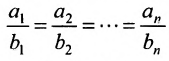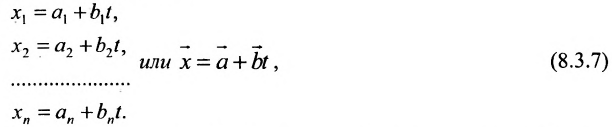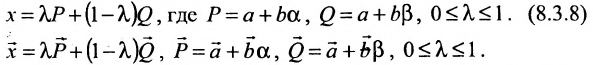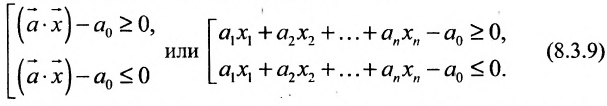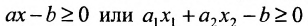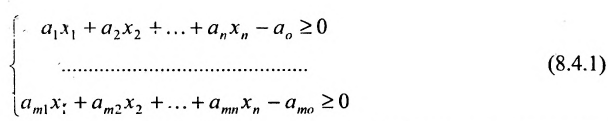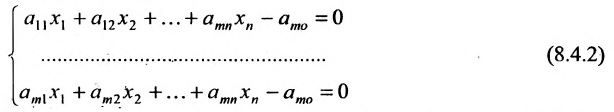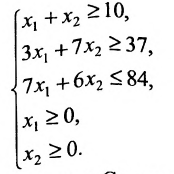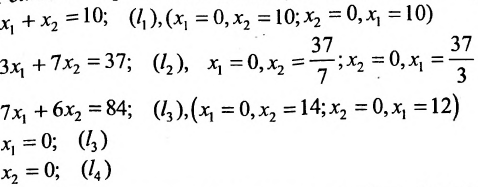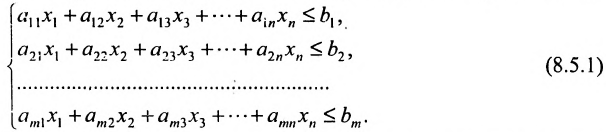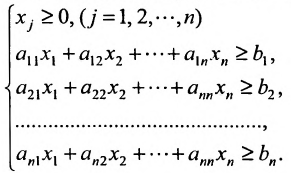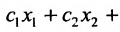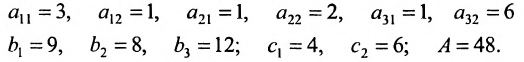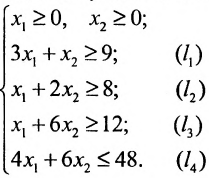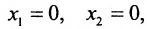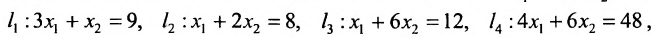В данной статье будут изучены вопросы параллельности плоскостей. Дадим определение плоскостям, которые параллельны между собой; обозначим признаки и достаточные условия параллельности; рассмотрим теорию на иллюстрациях и практических примерах.
- Параллельные плоскости: основные сведения
- Параллельность плоскостей: признак и условия параллельности
- Плоскость в трехмерном пространстве с примерами решения
- Взаимное расположение двух плоскостей, прямой и плоскости
- Понятие гиперплоскости
- Системы m линейных неравенств с n неизвестными
- Применение систем линейных неравенств в экономических исследованиях
- Глава 32. Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей
- 💡 Видео
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Параллельные плоскости: основные сведения
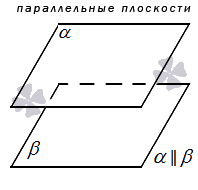
Параллельные плоскости – плоскости, не имеющие общих точек.
Чтобы обозначить параллельность применяют такой символ: ∥ . Если заданы две плоскости: α и β , являющиеся параллельными, краткая запись об этом будет выглядеть так: α ‖ β .
На чертеже, как правило, плоскости, параллельные друг другу, отображаются как два равных параллелограмма, имеющих смещение относительно друг друга.
В речи параллельность можно обозначить так: плоскости α и β параллельны, а также – плоскость α параллельна плоскости β или плоскость β параллельна плоскости α .
Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Параллельность плоскостей: признак и условия параллельности
В процессе решения геометрических задач зачастую возникает вопрос: а параллельны ли заданные плоскости между собой? Для получения ответа на этот вопрос используют признак параллельности, который также является достаточным условием параллельности плоскостей. Запишем его как теорему.
Плоскости являются параллельными, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Доказательство этой теоремы приводится в программе геометрии за 10 — 11 класс.
В практике для доказательства параллельности, в том числе, применяют две следующие теоремы.
Если одна из параллельных плоскостей параллельна третьей плоскости, то другая плоскость или также параллельна этой плоскости, или совпадает с ней.
Если две несовпадающие плоскости перпендикулярны некоторой прямой, то они параллельны.
На основе этих теорем и самого признака параллельности доказывается факт параллельности любых двух плоскостей.
Рассмотрим подробнее необходимое и достаточное условие параллельности плоскостей α и β , заданных в прямоугольной системе координат трехмерного пространства.
Допустим, что в некоторой прямоугольной системе координат задана плоскость α, которой соответствует общее уравнение A 1 x + B 1 y + C 1 z + D 1 = 0 , а также задана плоскость β , которую определяет общее уравнение вида A 2 x + B 2 y + C 2 z + D 2 = 0 .
Для параллельности заданных плоскостей α и β необходимо и достаточно, чтобы система линейных уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 не имела решения (являлась несовместной).
Предположим, что заданные плоскости, определяемые уравнениями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 являются параллельными, а значит не имеют общих точек. Таким образом, не существует ни одной точки в прямоугольной системе координат трехмерного пространства, координаты которой отвечали бы условиям одновременно обоих уравнений плоскостей, т.е. система A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 не имеет решения. Если указанная система не имеет решений, тогда не существует ни одной точки в прямоугольной системе координат трехмерного пространства, чьи координаты одновременно отвечали бы условиям обоих уравнений системы. Следовательно, плоскости, заданные уравнениями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 не имеют ни одной общей точки, т.е. они параллельны.
Разберем использование необходимого и достаточного условия параллельности плоскостей.
Заданы две плоскости: 2 x + 3 y + z — 1 = 0 и 2 3 x + y + 1 3 z + 4 = 0 . Необходимо определить, являются ли они параллельными.
Решение
Запишем систему уравнений из заданных условий:
2 x + 3 y + z — 1 = 0 2 3 x + y + 1 3 z + 4 = 0
Проверим, возможно ли решить полученную систему линейных уравнений.
Ранг матрицы 2 3 1 2 3 1 1 3 равен одному, поскольку миноры второго порядка равны нулю. Ранг матрицы 2 3 1 1 2 3 1 1 3 — 4 равен двум, поскольку минор 2 1 2 3 — 4 отличен от нуля. Таким образом, ранг основной матрицы системы уравнений меньше, чем ранг расширенной матрицы системы.
Совместно с этим, из теоремы Кронекера-Капелли следует: система уравнений 2 x + 3 y + z — 1 = 0 2 3 x + y + 1 3 z + 4 = 0 не имеет решений. Этим фактом доказывается, что плоскости 2 x + 3 y + z — 1 = 0 и 2 3 x + y + 1 3 z + 4 = 0 являются параллельными.
Отметим, что, если бы мы применили для решения системы линейных уравнений метод Гаусса, это дало бы тот же результат.
Ответ: заданные плоскости параллельны.
Необходимое и достаточное условие параллельности плоскостей возможно описать по-другому.
Чтобы две несовпадающие плоскости α и β были параллельны друг другу необходимо и достаточно, чтобы нормальные векторы плоскостей α и β являлись коллинеарными.
Доказательство сформулированного условия базируется на определении нормального вектора плоскости.
Допустим, что n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) являются нормальными векторами плоскостей α и β соответственно. Запишем условие коллинеарности данных векторов:
n 1 → = t · n 2 ⇀ ⇔ A 1 = t · A 2 B 1 = t · B 2 C 1 = t · C 2 , где t – некое действительное число.
Таким образом, чтобы несовпадающие плоскости α и β с заданными выше нормальными векторами были параллельны, необходимо и достаточно, чтобы имело место действительное число t , для которого верно равенство:
n 1 → = t · n 2 ⇀ ⇔ A 1 = t · A 2 B 1 = t · B 2 C 1 = t · C 2
В прямоугольной системе координат трехмерного пространства заданы плоскости α и β . Плоскость α проходит через точки: A ( 0 , 1 , 0 ) , B ( — 3 , 1 , 1 ) , C ( — 2 , 2 , — 2 ) . Плоскость β описывается уравнением x 12 + y 3 2 + z 4 = 1 Необходимо доказать параллельность заданных плоскостей.
Решение
Удостоверимся, что заданные плоскости не совпадают. Действительно, так и есть, поскольку координаты точки A не соответствуют уравнению плоскости β .
Следующим шагом определим координаты нормальных векторов n 1 → и n 2 → , соответствующие плоскостям α и β . Также проверим условие коллинеарности этих векторов.
Вектор n 1 → можно задать, взяв векторное произведение векторов A B → и A C → . Их координаты соответственно: ( — 3 , 0 , 1 ) и ( — 2 , 2 , — 2 ) . Тогда:
n 1 → = A B → × A C → = i → j → k → — 3 0 1 — 2 1 — 2 = — i → — 8 j → — 3 k → ⇔ n 1 → = ( — 1 , — 8 , — 3 )
Для получения координат нормального вектора плоскости x 12 + y 3 2 + z 4 = 1 приведем это уравнение к общему уравнению плоскости:
x 12 + y 3 2 + z 4 = 1 ⇔ 1 12 x + 2 3 y + 1 4 z — 1 = 0
Таким образом: n 2 → = 1 12 , 2 3 , 1 4 .
Осуществим проверку, выполняется ли условие коллинеарности векторов n 1 → = ( — 1 , — 8 , — 3 ) и n 2 → = 1 12 , 2 3 , 1 4
Так как — 1 = t · 1 12 — 8 = t · 2 3 — 3 = t · 1 4 ⇔ t = — 12 , то векторы n 1 → и n 2 → связаны равенством n 1 → = — 12 · n 2 → , т.е. являются коллинеарными.
Ответ: плоскости α и β не совпадают; их нормальные векторы коллинеарные. Таким образом, плоскости α и β параллельны.
Видео:10 класс, 10 урок, Параллельные плоскостиСкачать

Плоскость в трехмерном пространстве с примерами решения
Содержание:
Общее уравнение плоскости:
Пусть
которое называется уравнением плоскости, проходящей через точку 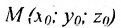
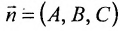

где 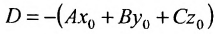
Приведём уравнение плоскости (8.1.2) к специальному виду. Для этого перенесём свободный член в правую часть уравнения: 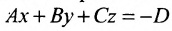
Разделим обе части уравнения на —D получим:
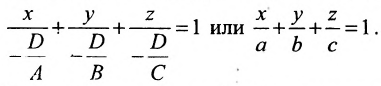
Это и есть специальный вид уравнения плоскости или уравнение плоскости «в отрезках», где а, b, с — величины отрезков, которые отсекает плоскость на координатных осях.
Если плоскость проходит через точки 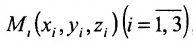
Разложив данный определитель по элементам первой строки, придём к уравнению вида (8.1.1).
Уравнения (8.1.1), (8.1.3), (8.1.4) можно привести к виду (8.1.2).
Пример:
Составить уравнение плоскости, проходящей через точки А(0, -2, -1), В(2, 4, -2) и С(3, 2, 0).
Решение:
Воспользуемся формулой (8.1.4), где
Подставив координаты точек A, В и С, получим: 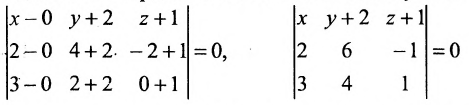
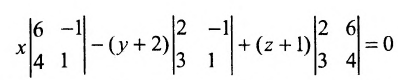
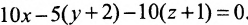
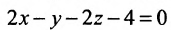
Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Взаимное расположение двух плоскостей, прямой и плоскости
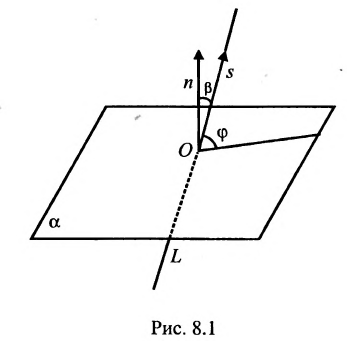
Углом между прямой и плоскостью будем называть угол, образованный прямой и ее проекцией на плоскость (рис. 8.1). Пусть прямая L и плоскость а заданы уравнениями:
Рассмотрим направляющий вектор 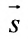
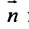
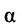
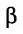
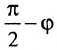
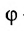
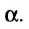
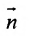
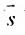
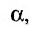
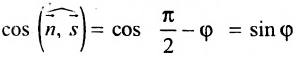
Если угол 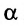
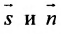
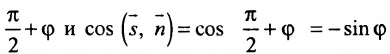
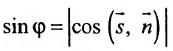
Условие перпендикулярности прямой и плоскости. Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор 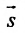
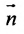
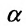
Условие параллельности прямой и плоскости. Прямая L и плоскость 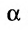
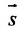
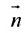
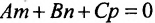
Пример:
Написать уравнение плоскости, проходящей через точку 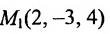
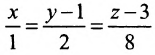
Решение:
Так как 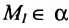
Применяя условие параллельности (8.2.3) прямой и плоскости, получим систему линейных уравнений
где
Решив систему, найдем:
Подставив найденные значения коэффициентов А,В,С, полУ
чим искомое уравнение плоскости:
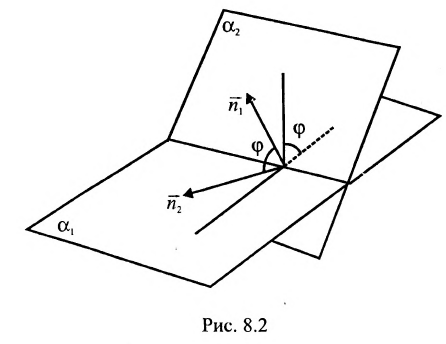
Угол между плоскостями. Рассмотрим две плоскости 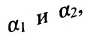
Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно,
что угол между нормальными векторами 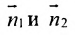
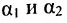
или 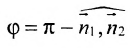
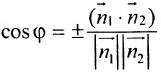
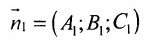
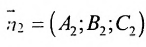
Пример:
Определить угол между плоскостями
Решение:
Воспользовавшись формулой (8.2.4), получим:
Условие параллельности двух плоскостей. Две плоскости 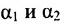
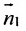
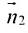
Векторы параллельны, если их координаты пропорциональны:
Две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы 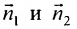
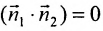
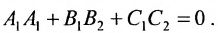
Пример:
Составить уравнение плоскости, проходящей через точку M(-2, 1, 4) параллельно плоскости 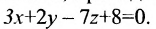
Решение:
Уравнение плоскости будем искать в виде 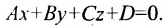
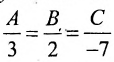
Так как 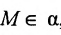
Пример:
Составить уравнение плоскости, проходящей через точки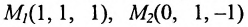
Решение:
Так как 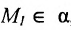
Далее, так как 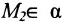
Учитывая, что заданная плоскость перпендикулярна искомой, составим еще одно уравнение: A+B+С=0. Получим систему:
Выразив коэффициенты А и В через С: А = -2 С, В=С и подставив их в уравнение (8.2.7), -2С (х-1)+С (у-1)+С (z-l)=0, определяем искомое уравнение: —2х + у +z = 0 .
Понятие гиперплоскости
Взаимное расположение гиперплоскостей:
Рассмотрим n-мерное векторное пространство Пусть вектор 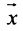
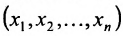
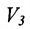
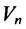
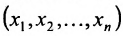
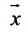
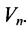
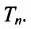
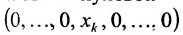
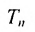
Совокупность точек 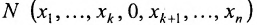
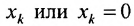
Определение 8.3.1. Гиперплоскостью в п-мериом пространстве 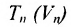
где 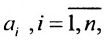
Заметим, что все 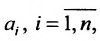
Рассмотрим две гиперплоскости:
Множество точек, принадлежащих как первой, так и второй гиперплоскости, называется их пересечением.
Теорема 8.3.1. Две гиперплоскости (8.3.2) и (8.3.3) не пересекаются в том и только в том случае, когда коэффициенты при соответствующих неизвестных пропорциональны, а свободные члены находятся в ином отношении:
Доказательство. Пусть гиперплоскости (8.3.2) и (8.3.3) не пересекаются. Следовательно, они не имеют общих точек и система
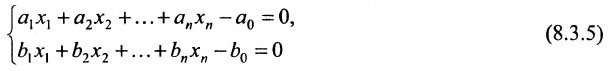
И наоборот, если система несовместна, то гиперплоскости (8.3.2) и (8.3.3) не пересекаются.
В силу теоремы Кронекера- Капелли система (8.3.5) несовместна, если ранг матрицы не равен рангу расширенной матрицы системы. А так как ранг расширенной матрицы системы не больше 2, то ранг матрицы системы должен ть равен 1. Эта возможность выражается условием (8.3.4).Поскольку для того, чтобы матрица 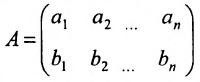
Ранг матрицы 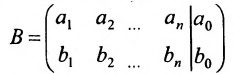
Теорема 8.3.2. Для того, чтобы уравнения (8.3.2) и (8.3.3) определят одну и ту же гиперплоскость, необходимо и достаточно, чтобы выполнялись условия:
Доказательство. Достаточность. Пусть условия (8.3.6) выполнены. Обозначим отношения через t, т.е.
Тогда уравнение (8.3.2) можно получить из (8.3.3) умножением всех его членов на t. Поэтому уравнения равносильны и, следовательно, определяют одну и ту же гиперплоскость.
Необходимость. Пусть уравнения (8.3.2) и (8.3.3) определяют одну и ту же гиперплоскость. Система (8.3.5) совместна и, следовательно, ранг матрицы системы равен рангу расширенной матрицы. И т.к. эта система определяет одну гиперплоскость, то каждое из уравнений можно рассматривать как систему. Поэтому ранг этой системы равен 1 и все миноры второго порядка равны нулю, т.е.
Откуда следует, что
Определение 8.3.2. Две гиперплоскости называются параллель-ными, если они не пересекаются или совпадают.
Тогда из теорем 8.3.1 и 8.3.2 вытекает
Теорема 8.3.3. Две гиперплоскости (8.3.2) и (8.3.3) параллельны тогда и только тогда, когда соответствующие коэффициенты
пропорциональны, т.е.
Введем понятие прямой в n мерном пространстве по аналогии с параметрическими уравнениями прямой в трехмерном пространстве.
Определение 8.3.3. Прямой в 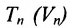
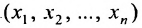
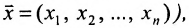
где 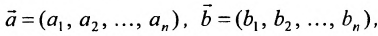
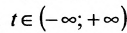
Определение 8.3.4. Отрезком в 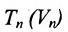
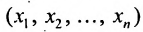
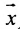
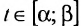
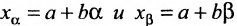
Теорема 8.3.4. Всякая точка отрезка может быть выражена линейной комбинацией его концов:
Если в трехмерном пространстве провести плоскость, то она разделит его на две части, называемые полупространствами. Очевидно, и гиперплоскость разделит n-мерное пространство на полупространства, т.е. справедливо.
Определение 8.3.5. Полупространствами, порождаемыми гиперплоскостью 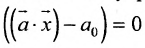
Гиперплоскость принадлежит обоим полупространствам, является их общей частью. Из (8.3.9) следует, что любое линейное неравенство геометрически определяет полупространство соответствующей размерности.
Определение 8.3.6. Множество точек 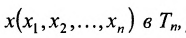
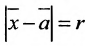
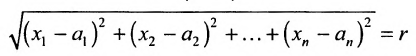
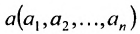
Системы m линейных неравенств с n неизвестными
В элементарной математике мы познакомились с линейными неравенствами одного или двух переменных:
Решением таких неравенств является промежуток числовой оси или полуплоскость.
Рассмотрим теперь линейное неравенство с n переменными:
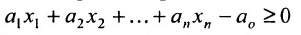
Несколько неравенств, рассматриваемых совместно, образуют систему:
Определение 8.4.1. Областью решений системы т неравенств с п неизвестными называется множество точек пространства 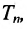
Из того факта, что областью решения линейного неравенства является полупространство, вытекает
Теорема 8.4.1. Область решений системы линейных неравенств есть пересечение некоторого числа полупространств.
Это пересечение является выпуклым множеством; оно ограничено гиперплоскостями
Так как линейные неравенства (8.4.1) независимы, то система (8.4.2) при m-n будет либо определённой, либо несовместной. И, следовательно, пересечение n гиперплоскостей в n-мерном пространстве либо даёт точку, либо не содержит ни одной точки.
Так как число систем по n уравнений с n неизвестными, которое может быть получено из (8.4.2) не может быть сколь угодно большим, и так как не всякая точка пересечения гиперплоскостей (является решением) принадлежит пересечению всех m гиперплоскостей, то число крайних точек, т.е. точек пересечения гиперплоскостей, принадлежащих данному множеству, ограничено. Следовательно, рассматриваемое множество будет многогранником, а крайние точки — его вершинами.
Итак, .областью решений совместной системы линейных нера-qchqtb является выпуклый многогранник, гранями которого служат некоторые части гиперплоскостей.
Пример:
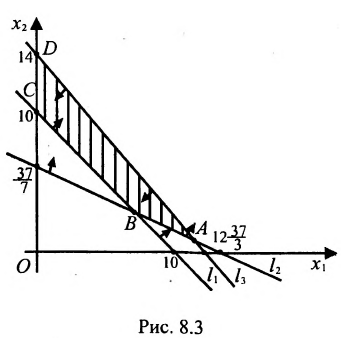
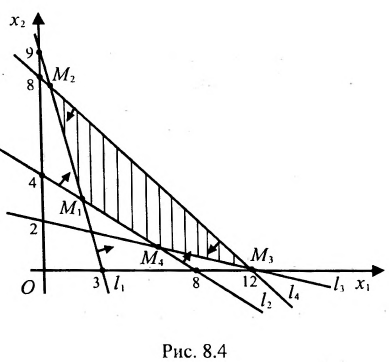
Найти решение системы линейных неравенств
Решение:
Строим на плоскости 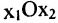
соответствующие заданным неравенствам (рис. 8.3). Каждая из них делит плоскость на две полуплоскости, одна из которых является решением соответствующего неравенства. Для выбора полуплоскости, являющейся решением неравенства, подставляем начало координат О (0, 0) в каждое неравенство. Если получаем верное неравенство, то полуплоскость, содержащая начало координат, является решением неравенства, в противном случае — полуплоскость, не содержащая начало координат, является решением неравенства.
Стрелки указывают полуплоскости, являющиеся областями решений данных неравенств. Пересечение отмеченных полуплоскостей- заштрихованный четырехугольник АВСД на рис. 8.3- область решения данной системы.
Применение систем линейных неравенств в экономических исследованиях
Рассмотрим систему m линейных неравенств с n переменными:
Каждое неравенство системы определяет полупространство. Решением системы (8.5.1) является пересечение этих полупространств.
Системы линейных неравенств широко применяются во многих экономических задачах, в частности, при построении линейной модели производства. Производственный способ описывает производство продукции и расход ресурсов в единицу времени. Он математически задается вектором выпуска или вектором валовой продукции 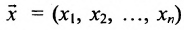
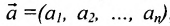
Если в производственной системе используется m видов производственных ресурсов, определены запасы ресурса i при использовании j-той технологии, то модель производственной системы математически приобретает вид системы линейных неравенств (8.5.1), в которой 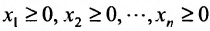
Пример:
Пусть известно содержание питательных веществ в единице каждого из имеющихся в хозяйстве кормов. Известна также цена каждого корма. Требуется определить все возможные рационы для кормления скота, которые удовлетворяли бы суточную потребность в каждом питательном веществе, а общая стоимость используемых кормов не превосходила бы A.
Решение:
Введем обозначения: m — число питательных веществ; n — число изменяющихся видов кормов; 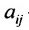
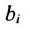
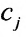
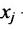
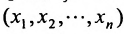
Задача рациона формулируется следующим образом: определить рацион 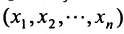
стоимость которого ограничена величиной А: 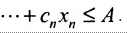
Например, пусть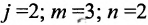
Тогда получаем систему:
Определим множество решений данной системы на плоскости 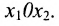
(рис. 8.4) соответствующие данным неравенствам. Каждая из них делит плоскость на две полуплоскости, одна из которых является решением соответствующего неравенства. Для выбора полуплоски являющейся решением неравенства, подставляем 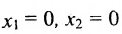
Если получаем верное неравенство, то полуплоскость, содержащая начало координат, является решением неравенства, в противном случае — полуплоскость, не содержащая начало координат, является решением неравенства.
Стрелки на прямых указывают полуплоскости, являющиеся областями решений данных неравенств. Заштрихованный четырехугольник 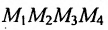
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Функция одной переменной
- Производная функции одной переменной
- Приложения производной функции одной переменной
- Исследование поведения функций
- Ранг матрицы — определение и вычисление
- Определители второго и третьего порядков и их свойства
- Метод Гаусса — определение и вычисление
- Прямая линия на плоскости и в пространстве
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Глава 32. Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей
Один из углов f между плоскостями A1x + B1y + C1z + D1 = 0 и
A2x +B2y + C2z + D2 = 0 (рис. 2.18.1) равен углу между их нормальными векторами 

Найти угол между плоскостями x – y + 21/2z + 2 = 0 и x + y +21/2z – 3 = 0.
Условие параллельности плоскостей
Две плоскости параллельны тогда и только тогда, когда их нормальные векторы 

Определить, параллельны ли плоскости 2x–3y–4z+11=0 и –4x+6y+8z+36=0.
Плоскости параллельны, так как
Условие перпендикулярности плоскостей
Если две плоскости заданы уравнениями A1x1 + B1y1 + C1z1 + D = 0, A2x2 + B2y2 + C2z2 + D = 0, то условием их перпендикулярности является
A1A2 + B1B2 + C1C2 = 0.
Если плоскости перпендикулярны, то перпендикулярны и их нормальные векторы N1 и N2.
Определить перпендикулярны ли плоскости 3x–2y–2z+7=0 и 2x+2y+z+4=0.
Так как 3×2+(–2)×2+(–2) ×1=0, то заданные плоскости перпендикулярны.
Плоскость, проходящая через данную точку параллельно данной плоскости
Плоскость, проходящая через точку M1(x1;y1;z1) и параллельная плоскости Ax+By+Cz+D=0, представляется уравнением
A(x–x1) + B(y–y1) + C(z–z1) = 0.
Написать уравнение плоскости, проходящей через точку (2;–1;6) параллельно плоскости x+y–2z+5=0.
(x–2) + (y+1) –2(z–6) = 0, т. е. x + y – 2z + 11 = 0.
Плоскость, проходящая через две точки перпендикулярно к данной плоскости
Плоскость P, проходящая через две точки M0(x0,y0,z0) и M1(x1,y1,z1) перпендикулярно к плоскости Q, заданной уравнением Ax+By+Cz+D=0, представляется уравнением
Написать уравнение плоскости, проходящей через две точки: M0(1;2;3) и M1(2;1;1) перпендикулярно к плоскости 3x+4y+z–6=0.
Плоскость представляется уравнением:

Расстояние от точки до плоскости
Расстояние от точки M1(x1;y1;z1) до плоскости Ax+By+Cz+D=0 равно
Найти расстояние от точки (3;9;1) до плоскости x–2y+2z–3=0.
💡 Видео
Параллельные прямые | Математика | TutorOnlineСкачать

ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ 10 класс стереометрияСкачать

Параллельность прямых. 10 класс.Скачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

10 класс, 5 урок, Параллельность трех прямыхСкачать

10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Параллельность прямой к плоскостиСкачать

Лекция 25. Виды уравнений плоскости в пространстве.Скачать

10. Параллельные плоскостиСкачать

9. Угол между плоскостями Условия параллельности и перпендикулярности плоскостейСкачать

10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

Уравнение плоскости через 2 точки параллельно прямойСкачать