Плоскость заданная уравнением ax by cz d 0 параллельна плоскости yoz если (5 видео)

Содержание

Плоскость заданная уравнением ax by cz d 0 параллельна плоскости yoz если
Плоскость заданная уравнением ax by cz d 0 параллельна плоскости yoz если
При каком условии плоскость, заданная уравнением ах + by+ cz+ d= 0. ГДЗ. Геометрия. 10 класс. Погорелов. § 4 п.38 Задача 71
🔥 Видео

Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Плоскость заданная уравнением ax by cz d 0 параллельна плоскости yoz если

Если A = B = 0, т. е. уравнение имеет вид Cz + D = 0, или .

то вектор нормали коллинеарен вектору k = (0, 0, 1). Поэтому плоскость перпендикулярна оси OZ, а значит параллельна плоскости XOY. Координатная плоскость XOY имеет уравнение z = 0.

Аналогично, x = 0 — уравнение координатной плоскости YOZ; x = а — уравнение плоскости, параллельной YOZ; y = 0 — уравнение плоскости XOZ; y = b — уравнение плоскости, параллельной XOZ.

Если равна нулю только одна из координат вектора нормали, то нормаль перпендикулярна, а плоскость, следовательно, параллельна соответствующей оси. Например, плоскость Ax + Cz + D = 0 параллельна оси OY (возможно, содержит эту ось).

Вопросы о взаимном расположении плоскостей решаются с помощью вектора нормали. Пусть две плоскости заданы своими уравнениями: A1x + B1y + C1z + D1 = 0 (плоскость P1), A2x + B2y + C2z + D2 = 0 (плоскость P2).

Запишем в краткой, символической форме условия параллельности и перпендикулярности плоскостей:

Угол между плоскостями равен углу между векторами нормали и находится с помощью скалярного произведения (см. раздел 4.2).

Пример 9. Найти угол между плоскостями 2x — 2y + z — 5 = 0, x — z + 7 = 0.

Решение. Найдём косинус угла между векторами нормали N1 = (2, —2, 1) и N2 = (1, 0, —1):

Используя таблицы или калькулятор, можно найти.

Как известно, через любые 3 точки, не лежащие на одной прямой, можно провести единственную плоскость. Научимся решать эту важную задачу в общем виде, а затем рассмотрим пример.

Пусть точки M1(x1, y1,z1), M2(x2,y2,z2), M3(x3,y3,z3) не лежат на одной прямой. Мы помним, что главное для записи уравнения плоскости — найти вектор нормали, т. е. какой-нибудь вектор, перпендикулярный плоскости. В качестве такого вектора можно взять векторное произведение:

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Плоскость заданная уравнением ax by cz d 0 параллельна плоскости yoz если

Теорема. Всякое невырожденное уравнение первой степени с тремя переменными описывает некоторую плоскость в пространстве, и наоборот: всякая плоскость может быть описана таким уравнением.

Ax + By + Cz + D = 0 — общее уравнение плоскости,

A 2 + B 2 + C 2 ¹ 0 — условие невырожденности.

Рассмотрим различные случаи расположения плоскости в пространстве в зависимости от коэффициентов общего уравнения.

1. D = 0, Ax + By + Cz = 0 — проходит через начало координат;

2. A = D = 0, By + Cz = 0 — содержит OX ;

Расстояние от точки M ₀ ( x ₀, y ₀, z ₀) до плоскости, заданной общим уравнением Ax + By + Cz + D = 0, вычисляется по формуле

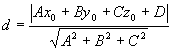
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

При каком условии плоскость, заданная уравнением ах + by+ cz+ d= 0. ГДЗ. Геометрия. 10 класс. Погорелов. § 4 п.38 Задача 71

Кто знает решение? При каком условии плоскость, заданная уравнением
ах + by+ cz+ d= 0: 1) параллельна оси z;2) проходит через ось г; 3) перпендикулярна плоскости xz?

Лови решение.
1 ) параллельные оси z;
2) проходит через ось z;
3) перпендикулярна плоскости xz? п = (а; b; с)
1) п ┴е3 = (0; 0; 1)) a∙0 + b∙ 0 + с· 1 =0;
с = 0 ( d ≠0, иначе плоскость содержит ось z)
2) с = d= 0
3) п ┴e2 а∙0 + b∙1 + с∙0 — 0 b = 0.