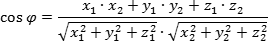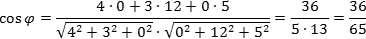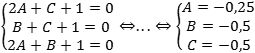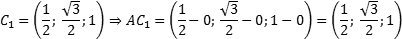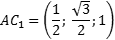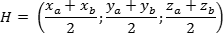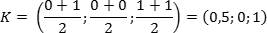Плоскость в пространстве заданная уравнениями 2y 3z 1 02y 3z 1 0 перпендикулярна плоскостям (8 видео)

Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой

Данная статья дает представление о том, как составить уравнение плоскости, проходящей через заданную точку трехмерного пространства перпендикулярно к заданной прямой. Разберем приведенный алгоритм на примере решения типовых задач.

Содержание

Нахождение уравнения плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой
Метод координат в пространстве
Вычисление координат векторов
Вычисление направляющих векторов для прямых
Вычисление нормальных векторов для плоскостей
Координаты середины отрезка
Геометрия. 11 класс
Математический портал
Nav view search
Navigation
Search
Плоскость в пространстве, всевозможные уравнения, расстояние от точки до плоскости.
🎬 Видео

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Нахождение уравнения плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой

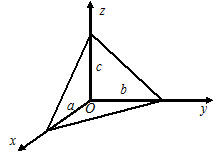
Пусть задано трехмерное пространство и прямоугольная система координат O x y z в нем. Заданы также точка М 1 ( x 1 , y 1 , z 1 ) , прямая a и плоскость α , проходящая через точку М 1 перпендикулярно прямой a . Необходимо записать уравнение плоскости α .

Прежде чем приступить к решению этой задачи, вспомним теорему геометрии из программы 10 — 11 классов, которая гласит:

Через заданную точку трехмерного пространства проходит единственная плоскость, перпендикулярная к заданной прямой.

Теперь рассмотрим, как же найти уравнение этой единственной плоскости, проходящей через исходную точку и перпендикулярной данной прямой.

Возможно записать общее уравнение плоскости, если известны координаты точки, принадлежащей этой плоскости, а также координаты нормального вектора плоскости.

Условием задачи нам заданы координаты x 1 , y 1 , z 1 точки М 1 , через которую проходит плоскость α . Если мы определим координаты нормального вектора плоскости α , то получим возможность записать искомое уравнение.

Нормальным вектором плоскости α , так как он ненулевой и лежит на прямой a , перпендикулярной плоскости α , будет являться любой направляющий вектор прямой a . Так, задача нахождения координат нормального вектора плоскости α преобразовывается в задачу определения координат направляющего вектора прямой a .

Определение координат направляющего вектора прямой a может осуществляться разными методами: зависит от варианта задания прямой a в исходных условиях. К примеру, если прямая a в условии задачи задана каноническими уравнениями вида

x — x 1 a x = y — y 1 a y = z — z 1 a z

или параметрическими уравнениями вида:

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ

то направляющий вектор прямой будет иметь координаты а x , а y и а z . В случае, когда прямая a представлена двумя точками М 2 ( x 2 , y 2 , z 2 ) и М 3 ( x 3 , y 3 , z 3 ) , то координаты направляющего вектора буду определяться как (x3 – x2, y3 – y2, z3 – z2).

Алгоритм для нахождения уравнения плоскости, проходящей через заданную точку перпендикулярно заданной прямой:

— определяем координаты направляющего вектора прямой a : a → = ( а x , а y , а z ) ;

— определяем координаты нормального вектора плоскости α как координаты направляющего вектора прямой a :

n → = ( A , B , C ) , где A = a x , B = a y , C = a z ;

— записываем уравнение плоскости, проходящей через точку М 1 ( x 1 , y 1 , z 1 ) и имеющей нормальный вектор n → = ( A , B , C ) в виде A ( x – x 1 ) + B ( y – y 1 ) + C ( z – z 1 ) = 0 . Это и будет являться требуемым уравнением плоскости, которая проходит через заданную точку пространства и перпендикулярна к данной прямой.

Полученное общее уравнение плоскости: A ( x – x 1 ) + B ( y – y 1 ) + C ( z – z 1 ) = 0 дает возможность получить уравнение плоскости в отрезках или нормальное уравнение плоскости.

Решим несколько примеров, используя полученный выше алгоритм.

Задана точка М 1 ( 3 , — 4 , 5 ) , через которую проходит плоскость, и эта плоскость перпендикулярна координатной прямой О z .

Решение

направляющим вектором координатной прямой O z будет координатный вектор k ⇀ = ( 0 , 0 , 1 ) . Следовательно, нормальный вектор плоскости имеет координаты ( 0 , 0 , 1 ) . Запишем уравнение плоскости, проходящей через заданную точку М 1 ( 3 , — 4 , 5 ) , нормальный вектор которой имеет координаты ( 0 , 0 , 1 ) :

A ( x — x 1 ) + B ( y — y 1 ) + C ( z — z 1 ) = 0 ⇔ ⇔ 0 · ( x — 3 ) + 0 · ( y — ( — 4 ) ) + 1 · ( z — 5 ) = 0 ⇔ z — 5 = 0

Ответ: z – 5 = 0 .

Рассмотрим еще один способ решить данную задачу:

Плоскость, которая перпендикулярна прямой O z будет задана неполным общим уравнением плоскости вида С z + D = 0 , C ≠ 0 . Определим значения C и D : такие, при которых плоскость проходит через заданную точку. Подставим координаты этой точки в уравнение С z + D = 0 , получим: С · 5 + D = 0 . Т.е. числа, C и D связаны соотношением — D C = 5 . Приняв С = 1 , получим D = — 5 .

Подставим эти значения в уравнение С z + D = 0 и получим требуемое уравнение плоскости, перпендикулярной к прямой O z и проходящей через точку М 1 ( 3 , — 4 , 5 ) .

Оно будет иметь вид: z – 5 = 0 .

Ответ: z – 5 = 0 .

Составьте уравнение плоскости, проходящей через начало координат и перпендикулярной к прямой x — 3 = y + 1 — 7 = z + 5 2

Решение

Опираясь на условия задачи, можно утверждать, что за нормальный вектор n → заданной плоскости можно принять направляющий вектор заданной прямой. Таким, образом: n → = ( — 3 , — 7 , 2 ) . Запишем уравнение плоскости, проходящей через точку О ( 0 , 0 , 0 ) и имеющей нормальный вектор n → = ( — 3 , — 7 , 2 ) :

— 3 · ( x — 0 ) — 7 · ( y — 0 ) + 2 · ( z — 0 ) = 0 ⇔ — 3 x — 7 y + 2 z = 0

Мы получили требуемое уравнение плоскости, проходящей через начало координат перпендикулярно к заданной прямой.

Ответ: — 3 x — 7 y + 2 z = 0

Задана прямоугольная система координат O x y z в трехмерном пространстве, в ней – две точки А ( 2 , — 1 , — 2 ) и B ( 3 , — 2 , 4 ) . Плоскость α проходит через точку A перпендикулярно прямой А В . Необходимо составить уравнение плоскости α в отрезках.

Решение

Плоскость α перпендикулярна к прямой А В , тогда вектор А В → будет нормальным вектором плоскости α . Координаты этого вектора определяются как разности соответствующих координат точек В ( 3 , — 2 , 4 ) и А ( 2 , — 1 , — 2 ) :

A B → = ( 3 — 2 , — 2 — ( — 1 ) , 4 — ( — 2 ) ) ⇔ A B → = ( 1 , — 1 , 6 )

Общее уравнение плоскости будет записано в следующем виде:

1 · x — 2 — 1 · y — ( — 1 + 6 · ( z — ( — 2 ) ) = 0 ⇔ x — y + 6 z + 9 = 0

Теперь составим искомое уравнение плоскости в отрезках:

x — y + 6 z + 9 = 0 ⇔ x — y + 6 z = — 9 ⇔ x — 9 + y 9 + z — 3 2 = 1

Ответ: x — 9 + y 9 + z — 3 2 = 1

Также нужно отметить, что встречаются задачи, требование которых – написать уравнение плоскости, проходящей через заданную точку и перпендикулярной к двум заданным плоскостям. В общем, решение этой задачи в том, чтобы составить уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой, т.к. две пересекающиеся плоскости задают прямую линию.

Задана прямоугольная система координат O x y z , в ней – точка М 1 ( 2 , 0 , — 5 ) . Заданы также уравнения двух плоскостей 3 x + 2 y + 1 = 0 и x + 2 z – 1 = 0 , которые пересекаются по прямой a . Необходимо составить уравнение плоскости, проходящей через точку М 1 перпендикулярно к прямой a .

Решение

Определим координаты направляющего вектора прямой a . Он перпендикулярен как нормальному вектору n 1 → ( 3 , 2 , 0 ) плоскости n → ( 1 , 0 , 2 ) , так и нормальному вектору 3 x + 2 y + 1 = 0 плоскости x + 2 z — 1 = 0 .

Тогда направляющим вектором α → прямой a возьмем векторное произведение векторов n 1 → и n 2 → :

a → = n 1 → × n 2 → = i → j → k → 3 2 0 1 0 2 = 4 · i → — 6 · j → — 2 · k → ⇒ a → = ( 4 , — 6 , — 2 )

Таким образом, вектор n → = ( 4 , — 6 , — 2 ) будет нормальным вектором плоскости, перпендикулярной к прямой a . Запишем искомое уравнение плоскости:

4 · ( x — 2 ) — 6 · ( y — 0 ) — 2 · ( z — ( — 5 ) ) = 0 ⇔ 4 x — 6 y — 2 z — 18 = 0 ⇔ ⇔ 2 x — 3 y — z — 9 = 0

Ответ: 2 x — 3 y — z — 9 = 0

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Метод координат в пространстве

Для того, чтобы использовать метод координат, надо хорошо знать формулы. Их три:

Главная формула — косинус угла φ между векторами a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂):

Уравнение плоскости в трехмерном пространстве: Ax + By + Cz + D = 0, где A, B, C и D — действительные числа, причем, если плоскость проходит через начало координат, D = 0. А если не проходит, то D = 1.

Вектор, перпендикулярный к плоскости Ax + By + Cz + D = 0, имеет координаты: n = (A; B; C).

На первый взгляд, выглядит угрожающе, но достаточно немного практики — и все будет работать великолепно.

Задача. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).

Решение. Поскольку координаты векторов нам даны, подставляем их в первую формулу:

Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.

Решение. Общее уравнение плоскости: Ax + By + Cz + D = 0, но, поскольку искомая плоскость не проходит через начало координат — точку (0; 0; 0) — то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K, то координаты этих точек должны обращать уравнение в верное числовое равенство.

Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем:
A · 2 + B · 0 + C · 1 + 1 = 0 ⇒ 2A + C + 1 = 0;

Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения:
A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;

Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений:

Получили, что уравнение плоскости имеет вид: − 0,25x − 0,5y − 0,5z + 1 = 0.

Задача. Плоскость задана уравнением 7x − 2y + 4z + 1 = 0. Найти координаты вектора, перпендикулярного данной плоскости.

Решение. Используя третью формулу, получаем n = (7; − 2; 4) — вот и все!

Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Вычисление координат векторов

А что, если в задаче нет векторов — есть только точки, лежащие на прямых, и требуется вычислить угол между этими прямыми? Все просто: зная координаты точек — начала и конца вектора — можно вычислить координаты самого вектора.

Чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала.

Эта теорема одинаково работает и на плоскости, и в пространстве. Выражение «вычесть координаты» означает, что из координаты x одной точки вычитается координата x другой, затем то же самое надо сделать с координатами y и z. Вот несколько примеров:

Задача. В пространстве расположены три точки, заданные своими координатами: A = (1; 6; 3), B = (3; − 1; 7) и C = (− 4; 3; − 2). Найти координаты векторов AB, AC и BC.

Рассмотрим вектор AB: его начало находится в точке A, а конец — в точке B. Следовательно, чтобы найти его координаты, надо из координат точки B вычесть координаты точки A:
AB = (3 − 1; − 1 − 6; 7 − 3) = (2; − 7; 4).

Аналогично, начало вектора AC — все та же точка A, зато конец — точка C. Поэтому имеем:
AC = (− 4 − 1; 3 − 6; − 2 − 3) = (− 5; − 3; − 5).

Наконец, чтобы найти координаты вектора BC, надо из координат точки C вычесть координаты точки B:
BC = (− 4 − 3; 3 − (− 1); − 2 − 7) = (− 7; 4; − 9).

Ответ: AB = (2; − 7; 4); AC = (− 5; − 3; − 5); BC = (− 7; 4; − 9)

Обратите внимание на вычисление координат последнего вектора BC: очень многие ошибаются, когда работают с отрицательными числами. Это касается переменной y: у точки B координата y = − 1, а у точки C y = 3. Получаем именно 3 − (− 1) = 4, а не 3 − 1, как многие считают. Не допускайте таких глупых ошибок!

Видео:Уравнение плоскости через точку и нормальСкачать

Вычисление направляющих векторов для прямых

Если вы внимательно прочитаете задачу C2, то с удивлением обнаружите, что никаких векторов там нет. Там только прямые да плоскости.

Для начала разберемся с прямыми. Здесь все просто: на любой прямой найдутся хотя бы две различные точки и, наоборот, любые две различные точки задают единственную прямую.

Кто-нибудь понял, что написано в предыдущем абзаце? Я и сам не понял, поэтому объясню проще: в задаче C2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим так называемый для прямой:

Зачем нужен этот вектор? Дело в том, что — это угол между их направляющими векторами. Таким образом, мы переходим от непонятных прямых к конкретным векторам, координаты которых легко считаются. Насколько легко? Взгляните на примеры:

Задача. В кубе ABCDA₁B₁C₁D₁ проведены прямые AC и BD₁. Найдите координаты направляющих векторов этих прямых.

Поскольку длина ребер куба в условии не указана, положим AB = 1. Введем систему координат с началом в точке A и осями x, y, z, направленными вдоль прямых AB, AD и AA₁ соответственно. Единичный отрезок равен AB = 1.

Теперь найдем координаты направляющего вектора для прямой AC. Нам потребуются две точки: A = (0; 0; 0) и C = (1; 1; 0). Отсюда получаем координаты вектора AC = (1 − 0; 1 − 0; 0 − 0) = (1; 1; 0) — это и есть направляющий вектор.

Теперь разберемся с прямой BD₁. На ней также есть две точки: B = (1; 0; 0) и D₁ = (0; 1; 1). Получаем направляющий вектор BD₁ = (0 − 1; 1 − 0; 1 − 0) = (− 1; 1; 1).

Ответ: AC = (1; 1; 0); BD₁ = (− 1; 1; 1)

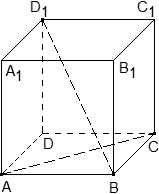
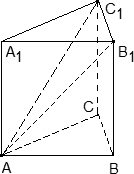
Задача. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, проведены прямые AB₁ и AC₁. Найдите координаты направляющих векторов этих прямых.

Введем систему координат: начало в точке A, ось x совпадает с AB, ось z совпадает с AA₁, ось y образует с осью x плоскость OXY, которая совпадает с плоскостью ABC.

Для начала разберемся с прямой AB₁. Тут все просто: у нас есть точки A = (0; 0; 0) и B₁ = (1; 0; 1). Получаем направляющий вектор AB₁ = (1 − 0; 0 − 0; 1 − 0) = (1; 0; 1).

Теперь найдем направляющий вектор для AC₁. Все то же самое — единственное отличие в том, что у точки C₁ иррациональные координаты. Итак, A = (0; 0; 0), поэтому имеем:

Небольшое, но очень важное замечание насчет последнего примера. Если начало вектора совпадает с началом координат, вычисления резко упрощаются: координаты вектора просто равны координатам конца. К сожалению, это верно лишь для векторов. Например, при работе с плоскостями присутствие на них начала координат только усложняет выкладки.

Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Вычисление нормальных векторов для плоскостей

Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.

Другими словами, — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.

Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).

Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:

Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение A₁BC₁. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A₁, B и C₁, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;

Аналогично, для точек B = (1; 0; 0) и C₁ = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;

Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.

Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).

Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение AA₁C₁C. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A₁ и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;

Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;

Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).

Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.

Видео:Найти уравнение плоскости проходящей через прямую и перпендикулярно плоскостиСкачать

Координаты середины отрезка

Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.

Итак, пусть отрезок задан своими концами — точками A = (x_a; y_a; z_a) и B = (x_b; y_b; z_b). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:

Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.

Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A₁B₁. Найдите координаты этой точки.

Поскольку точка K — середина отрезка A₁B₁, ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A₁ = (0; 0; 1) и B₁ = (1; 0; 1). Теперь найдем координаты точки K:

Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A₁B₁C₁D₁.

Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A₁L = C₁L, т.е. точка L — это середина отрезка A₁C₁. Но A₁ = (0; 0; 1), C₁ = (1; 1; 1), поэтому имеем:

Видео:3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

Геометрия. 11 класс

Декартовы координаты в пространстве

Найти косинус угла между прямыми АВ и КТ, если А(2, –1), В(3, 4), К(–2, 3), Т(4, 1).

Декартовы координаты в пространстве

Подчеркнуть плоскости, перпендикулярные данной плоскости.

Дано уравнение плоскости $x−2 y+3 z−4=0$

3)$9 x+24 y+13 z+34=0$

Декартовы координаты в пространстве

Выделить цветом прямые, проходящие через заданные точки, которые параллельны данной плоскости.

Дано уравнение плоскости $x+2 y−3 z−14=0$

1) $А(1, 2, 3), В(3, 2, 1)$

2) $С(-2, 1, 2), D(0, 3, 4)$

3) $A(1, 2, 3), D(0, 3, 4)$

4) $В(3, 2, 1), Е(5, 7, -3)$

5) $В(3, 2, 1), С(-2, 1, 2)$

Декартовы координаты в пространстве

Найти коэффициент, при котором плоскость будет перпендикулярна заданной плоскости $x+2 y+4 z=0$

Декартовы координаты в пространстве

Даны точки А(1, 2, 3), В(3, 2, 1), СD(–2, 1, 2), D(0, 3, 4), Е(5,7, –3), F(3, 3, 3). Установите соответствие

Декартовы координаты в пространстве

Даны три точки: A(0, 1, 2), B(4, 6, –3), C(2, 2, 2).

Написать уравнение плоскости ABC и заполнить пропуски в уравнении плоскости.

Декартовы координаты в пространстве

Соедините линиями объект и формулу. По плоскости раскиданы объекты. Нужно установить соответствие между названием искомого элемента и формулой для его нахождения

Видео:Лекция 25. Виды уравнений плоскости в пространстве.Скачать

Математический портал

Видео:Уравнение плоскости. 11 класс.Скачать

Nav view search

Search

Вы здесь:
Home
Аналитическая геометрия
Плоскость в пространстве, всевозможные уравнения, расстояние от точки до плоскости.

Видео:Эту задачу ГРИГОРИЙ ПЕРЕЛЬМАН решил в 10-м классеСкачать

Плоскость в пространстве, всевозможные уравнения, расстояние от точки до плоскости.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Существуют такие формы записи уравнения плоскости:

1) $Ax+By+Cz+D=0 -$ общее уравнение плоскости $P,$ где $overline=(A, B, C) -$ нормальный вектор плоскости $P.$

2) $A(x-x_0)+B(y-y_0)+C(z-z_0)=0 -$ уравнение плоскости $P,$ которая проходит через точку $M(x_0, y_0, z_0)$ перпендикулярно вектору $overline=(A, B, C).$ Вектор $overline N$ называется нормальным вектором плоскости.

4) $beginx-x_1&y-y_1&z-z_1\x_2-x_1&y_2-y_1&z_2-z_1\x_3-x_1&x_2-x_1&x_3-x_1end=0 — $ уравнение плоскости, которая проходит через три точки $A(x_1, y_1, z_1), B(x_2, y_2, z_2)$ и $C(x_3, y_3, z_3).$

5) $xcosalpha+ycosbeta+zcosgamma-p=0 -$ нормальное уравнение плоскости, где $cosalpha, cosbeta$ и $cosgamma -$ направляющие косинусы нормального вектора $overline,$ направленного из начала координат в сторону плоскости, а $p>0 -$ расстояние от начала координат до плоскости.

Общее уравнение плоскости приводится к нормальному, путем умножения на нормирующий множитель $mu=-frac<sqrt>.$

Расстояние от точки $M(x_0, y_0, z_0)$ до плоскости $P: Ax+By+Cz+D=0$ вычисляется по формуле $$d=left|frac<sqrt >right|.$$

Примеры:

2.180.

а) Заданы плоскость $P: -2x+y-z+1=0$ и точка $M(1, 1, 1).$ Написать уравнение плоскости $P’,$ проходящей через точку $M$ параллельно плоскости $P$ и вычислить расстояние $rho(P, P’).$

Решение.

Так как п.лоскости $P$ и $P’$ параллельны, то нормальный вектор для плоскости $P$ будет также нормальным вектором для плоскости $P’.$ Из уравнения плоскости получаем $overline=(-2, 1, -1).$

Далее запишем уравнение плоскости по формуле ( 2): $A(x-x_0)+B(y-y_0)+C(z-z_0)=0 -$ уравнение плоскости, которая проходит через точку $M(x_0, y_0, z_0)$ перпендикулярно вектору $overline=(A, B, C).$

Ответ: $-2x+y-z+2=0.$

2.181.

а) Написать уравнение плоскости $P’,$ проходящей через заданные точки $M_1(1, 2, 0)$ и $M_2(2, 1, 1)$ перпендикулярно заданной плоскости $P: -x+y-1=0.$

Решение.