2018-05-31 
Уравнение бегущей плоской звуковой волны имеет вид $chi = 60 cos (1800t — 5,3x)$, где $chi$ в микрометрах, $t$ в секундах, $x$ в метрах. Найти:
а) отношение амплитуды смещения частиц среды к длине волны;
б) амплитуду колебаний скорости частиц среды и ее отношение к скорости распространения волны;
в) амплитуду колебаний относительной деформации среды и ее связь с амплитудой колебания скорости частиц среды.
$xi = 60 cos (1800 t 5 cdot 3 x)$
$xi = a cos ( omega t — kx)$, где $a = 60 cdot 10^ м$
$omega = 1800 $ в секунду и $k = 5,3$ на метр
и $k = frac$, поэтому $v = frac = 340 м/с$
Таким образом, амплитуда колебаний скорости
$left ( frac right )_ $ или $v_ = a omega = 0,11 м / с$ (1)
и искомое отношение амплитуды колебаний скорости к скорости распространения волны
(в) Относительная деформация $= frac = ak sin ( omega t — kx) $
Таким образом, относительная амплитуда деформации
$= left ( frac right )_ = ak = (60 cdot 10^ cdot 5,3) м = 3,2 cdot 10^ м$ (2)
Видео:Урок 95 (осн). Механические волны. ЗвукСкачать

Клуб студентов «Технарь». Уникальный сайт с дипломами и курсовыми для технарей.
Все разделы / Физика /
Задачи по физике 3
Тип работы: Задачи
Форматы файлов: Microsoft Word
Описание:
Задача № 1
Однородный шар диаметром 80 см. совершает колебания вокруг горизонтальной оси, проходящей сквозь шар на расстоянии L=16 см. от его центра.
Определить период и циклическую частоту затухающих колебаний. Составить дифференциальное уравнение гармонических колебаний для углового смещения шара, пользуясь основным уравнением динамики вращательного движения (аналог 2 –го закона Ньютона) и записать его решение. Положить амплитуду колебаний φm=0,085 рад.
Задача № 2
Последовательный электрический контур содержит две катушки индуктивности L1=0,05 Гн и L2=0,075 Гн, разделенных емкостью C=0,02 мкФ и сопротивлением R=800 Ом, соединенных последовательно. Исходя из 2 закона Кирхгоффа, составить дифференциальное уравнение колебаний электрического заряда, записать его решение и определить циклическую частоту и период затухающих колебаний. Определить время, за которое энергия электрического поля конденсатора уменьшится в 7,34 раза.
Задача № 3
Определить добротность L-R-C последовательного электрического контура, содержащего периодическую ЭДС, если индуктивность катушки L =2,5 Гн, активное сопротивление контура R=0,125 Ом, а максимальное значение напряжения на обкладках конденсатора Um = 50 В достигается при частоте ν=9,28 Гц. Считая затухание малым, определить резонансную амплитуду колебаний.
Задача № 4
Плоская звуковая волна, уравнение которой в единицах СИ имеет вид:
Y(x,t)=2,5*10-6cos103π(t-(x/330)), распространяется в воздухе, плотность которого 0,0012 г/см3.
Определить энергию, переносимую волной за одну минуту сквозь площадку 12 см2, перпендикулярно распространению волны. При решении задачи следует учесть, что среднее значение квадрата синуса за период равно 0,5.
Задача № 5
Определить показатель преломления тонкого прозрачного клина, освещаемого монохроматическим светом с длиной волны 0,48 мкм, падающим нормально на его поверхность, если расстояние между смежными интерференционными максимумами в отраженном свете равно 0,32 мм.
Задача № 6
Из смотрового окошечка печи площадью S=6 см2 излучается поток Фэ=2040 Дж/мин. Считая излучение близким к излучению абсолютно черного тела, определить температуру Т печи и частоту, на которую приходится максимум излучения.
Комментарии: 2013 г
Размер файла: 241 Кбайт
Фаил: (.doc)
Видео:4.2 Решение волновых уравнений Гельмгольца в виде плоских бегущих волнСкачать

Плоская звуковая волна уравнение которой в единицах си имеет вид
4.1. Механические колебания.
4.2. Электрические колебания.
4.3. Упругие волны. Акустика.
4.4. Электромагнитные волны. Излучение.
_______________________________________________________________________________________________
4.1. Механические колебания.
4.1.1. Гармонические колебания.
4.1. 1 -1. Частица совершает гармоническое колебание с амплитудой А и периодом Т = 12 с. Найти время t ₁ , за которое смещение частицы изменяется от 0 до А/2.
Решение:
Т = 12 с
х(0) = 0
х( t ₁) = А/2 (1)
t ₁ – ?
Так как начальное положение частицы х(0) = 0, то частица колеблется по закону синуса с начальной фазой ϕ ₀ = 0:
x = Asin ( ωt + ϕ ₀) или
x = Asinωt , (2)
где ω = 2 π / T – круговая частота.
С учётом условия (1), запишем (2) в виде:
х( t ₁) = Asin ( ωt ₁); А/2 = Asin ( (2 π / T ) t ₁ ); 1/2 = sin (2 πt ₁/ T ); 2 πt ₁/ T = π /6. Отсюда
t ₁ = T /12.
t₁ = 12/12 = 1 с.
Ответ: t₁ = T/12 = 1 c.
4.1.1-2. Определить период Т простых гармонических колебаний диска радиусом R = 40 см около горизонтальной оси, проходящей через образующую диска.
где − I момент инерции диска относительно оси вращения, проходящей через точку подвеса А (см. рис.); x = AO = R − расстояние от точки подвеса до центра тяжести О диска; m − масса диска; g = 9,8 м/с² − ускорение свободного падения.
Момент инерции I ₀ диска относительно оси симметрии диска:
I ₀ = mR ²/2.
По теореме Штейнера:
I = I₀ + mR². Имеем
I = mR²/2 + mR² = 3mR²/2. Тогда по (1)
Решение:
r ( t ) = A ( icosωt + jsinωt ) (1)
A = 0,5 м
ω = 5 с⁻¹
v − ?
an − ?
Представим (1) в виде:
r ( t ) = iAcosωt + jAsinωt (1*)
Радиус вектор r ( t ) точки: r ( t ) = ix + jy , где x , y − проекции радиус вектора соответственно на оси OX и OY ; i , j − единичные векторы (орты), направленные соответственно по оси OX и OY . Тогда (1*) примет вид
ix + jy = iAcosωt + jAsinωt ,
отсюда получим два уравнения
x = Acosωt , (*)
y = Asinωt . (**)
Возведём их в квадрат
x ² = A ² cos ² ωt ,
y ² = A ² sin ² ωt .
Сложим эти уравнения
x ² + y ² = A ² cos ² ωt + A ² sin ² ωt или x ² + y ² = A ²( cos ² ωt + sin ² ωt ). Отсюда, т.к. cos ² ωt + sin ² ωt = 1, получим уравнение траектории движения точки
x ² + y ² = A ². (2)
Уравнение (2) − это уравнение окружности радиусом R = A = 0,5 м с центром в начале координат (см. рис.).
Найдём проекции скорости v x и vy . Для этого продифференцируем x и y из (*) и (**) по времени t :
vx = xt ʹ = ( Acosωt ) t ʹ = — Aωsinωt ;
vy = yt ʹ = ( Asinωt ) t ʹ = Aωcosωt .
Тогда квадрат скорости
v ² = vx ² + vy ² или v ² = (- Aωsinωt )² + ( Aωcosωt )² или v ² = A ² ω ²( sin ² ωt + cos ² ωt ) или v ² = A ² ω ². Отсюда модуль скорости v :
v = Aω . (3)
v = 0,5·5 = 2,5 м/с².
Модуль нормального ускорения an : an = v ²/ R или, с учётом (3) и R = A , получим an = A ² ω ²/ A или
an = Aω ².
an = 0,5·5² = 12,5 м/с².
Ответ: траектория − окружность радиусом R = A = 0,5 м с центром в начале координат, v = Aω = 2,5 м/с², an = Aω ² = 12,5 м/с².
_______________________________________________________________________________________________
4.1.2. Свободные затухающие колебания.
4.1.2-1. Амплитуда затухающих колебаний уменьшилась в n = 100 за 15 с. Чему равен коэффициент затухания β ?
Решение:
t = 15 c
n = 100
A = A ₀/ n (*)
β – ?
Зависимость амплитуды А затухающих колебаний от времени t :
A = A ₀ e — β t , (1)
где A ₀ – начальная амплитуда; β – коэффициент затухания.
Имеем из (1) и (*):
A ₀/ n = A ₀ e — β t ; 1/ n = e — β t ; e β t = n ; βt = ln ( n ) отсюда
β = ln ( n )/ t .
β = ln(100)/15 = 0,307 1/c.
Ответ: β = ln(n)/t = 0,307 1/c.
4.1.2-2. Найти логарифмический декремент затухания тонкого стержня, подвешенного за один из его концов, если за промежуток времени t = 5 мин его полная механическая энергия уменьшилась в n = 4 · 10 ² раз. Длина стержня L = 50 см.
Решение:
t = 5 мин = 300 с
n = 400
L = 0,5 м
λ − ?
В данном случае стержень − это физический маятник.
Логарифмический декремент затухания λ
λ = βT , (1)
где β – коэффициент затухания, T − период колебаний стержня.
1. Найдём коэффициент затухания β .
Связь частот ω и ω₀:
ω² = ω₀² — β². (2)
ω – частота затухающих колебаний; ω ₀ – собственная частота колебаний.
Зависимость от времени t полной механической энергии Е физического маятника:
Е = E ₀ e -2 βt ,
где E ₀ – начальная (при t = 0) полная механическая энергия.
Отсюда имеем
n = Е ₀/ Е = Е ₀/( E ₀ e -2 βt ) = 1 /( e -2 βt ) = e 2 βt .
Получили n = e 2 βt . Прологарифмируем это равенство Ln ( n ) = 2 βt . Отсюда
β = Ln ( n )/(2 t ). (3)
2. Найдём период Т затухающих колебаний.
Оценим коэффициент β 2 по (3).
β = Ln (400)/(2 · 300) = 0,009986, отсюда
β ² = (0,009986)² ≈ 0,0000997.
Собственная частота колебаний физического маятника:
Подставим в (1) найденные β из (3) и Т из (4**) и, после упрощения, получим
4.1.2-3. Логарифмический декремент затухания тела, колеблющегося с частотой 50 Гц, равен 0,02. Определите: время, за которое амплитуда колебаний тела уменьшится в 20 раз; число колебаний тела, чтобы произошло подобное уменьшение амплитуды.
Решение:
ν = 50 Гц
λ = 0,02
n = 20
t − ?
N − ?
1. Пусть β – коэффициент затухания; T = 1/ ν – период, ν – частота колебаний. Логарифмический декремент затухания λ :
λ = βT или λ = β / ν , отсюда
β = λν . (1)
Амплитуда А затухающих колебаний
A = A ₀· e — βt ,
где A ₀ − начальная амплитуда (при t = 0).
Подставим сюда из условия задачи A = A ₀/ n :
A ₀/ n = A ₀· e — βt ,
отсюда e βt = n и, после логарифмирования, βt = Ln ( n ), отсюда
t = ( Ln ( n ) )/ β и, с учётом (1),
t = ( Ln ( n ) )/( λν ). (2)
2. Число колебаний N за время t :
N = t / T = tν = ( и, с учётом (2), ) = ν ( Ln ( n ) )/( λν ) или
N = ( Ln ( n ) )/ λ . (3)
3. Вычисления по формулам (2) и (3):
t = ( Ln (20) )/(0,02·50) ≈ 3 с.
N = ( Ln (20) )/0,02 ≈ 150.
Ответ: t = ( Ln ( n ) )/( λν ) ≈ 3 с; N = ( Ln ( n ) )/ λ ≈ 150.
4.1.2-4. Составьте дифференциальное уравнение гармонических свободных затухающих крутильных колебаний механической системы.
Решение:
Пусть система (например, тонкий однородный диск, подвешенный в горизонтальном положении к упругой нити) совершает крутильные колебания относительно закреплённой оси Z (ось нити). Пусть на диск действует упругая сила, проекция момента которой на ось Z равна
Mz = — kϕ , (1)
где k − постоянная, ϕ − угол поворота из положения равновесия. Знак “минус” указывает на то, что при отклонении системы на угол ϕ , момент упругой силы возвращает систему к положению равновесия. Поместим диск в вязкую среду ( например, жидкость ). Момент силы сопротивления Mc , действующий на диск, пропорционален угловой скорости ϕ ʹ:
M c = — ηϕ ʹ, (2)
где η − постоянная.
Уравнение динамики вращательного движения диска имеет вид
Iϕ ʹʹ = Mz + M c , (3)
где I – момент инерции диска относительно оси вращения.
С учётом (1) и (2), уравнение (3) примет вид Iϕ ʹʹ = — kϕ — ηϕ ʹ, отсюда
ϕ ʹʹ + ( η / I ) ϕ ʹ + ( k / I ) ϕ = 0.
Применив обозначения 2 β = η / I , ω ₀² = k / I , перепишем последнее уравнение:
ϕ ʹʹ + 2 βϕ ʹ + ω ₀² ϕ = 0.
Это дифференциальное уравнение описывает затухающие крутильные колебания механической системы.
Ответ: ϕ ʹʹ + 2 βϕ ʹ + ω ₀² ϕ = 0.
4.1.2-5. Найти добротность Q осциллятора, у которого отношение резонансной частоты ωрез к частоте затухающих колебаний ω равно η.
Решение:
ωрез/ω = η (*)
Q − ?
Пусть β − коэффициент затухания, ω₀ − собственная частота колебаний, T = 2π/ω − период затухающих колебаний, λ = βT = 2πβ/ω − логарифмический декремент затухания. Тогда добротность Q:
Q = π/λ = π/(2πβ/ω), или
Q = ω/(2β). (1)
Связь частот ω и ω₀:
ω² = ω₀² — β². (2)
Формула для резонансной частоты ωрез:
ωрез² = ω₀² — 2β². (3)
Из (2) вычтем (3)
ω² — ωрез² = (ω₀² — β²) — (ω₀² — 2β²), или
ω² — ωрез² = ω₀² — β² — ω₀² + 2β², или
ω² — ωрез² = β². (**)
С учётом условия (*) имеем ωрез = ωη. Тогда (**) примет вид
ω² — ω²η² = β², или
ω²(1 — η²) = β², отсюда
___________________________________________________________________________________
4.1.3. Вынужденные колебания. Резонанс.
4.1.3-1. Осциллятор массы m движется по закону x = Asinωt под действием вынуждающей силы Fₓ = F₀cosωt. Найти коэффициент затухания β осциллятора.
Решение:
m,
x = Asinωt,
Fₓ = F₀cosωt,
β − ?
Установившееся смещение х(t) осциллятора при вынужденных колебаниях:
x = Acos(ωt — ϕ), (1)
ω₀ − собственная частота колебаний осциллятора,
f₀ = F₀/m. (*)
Так как по условию смещение х(t) осциллятора x = Asinωt, то из (1) следует: ϕ = π/2
(т. к. cos(ωt — π/2) = sinωt). Тогда из (3) имеем:
где f₀ = F ₀/ m , m − масса осциллятора , β − коэффициент затухания, ω₀ − собственная частота колебаний, ω − частота вынужденных колебаний.
При постоянной амплитуде вынуждающей силы F ₀ (и, следовательно, постоянной f ₀) из (*) при двух разных частотах ω₁ и ω₂ получаем две амплитуды А₁ и А₂ вынужденных колебаний:
4.2. Электрические колебания.
4.2-1. Небольшая магнитная стрелка совершает малые колебания вокруг оси, перпендикулярной направлению внешнего магнитного поля. При изменении индукции этого поля период колебаний стрелки уменьшился в η = 5 раз. Во сколько раз и как изменилась индукция поля? Затухание колебаний пренебрежимо мало.
Решение:
T ₁/ T ₂ = η = 5
B ₂/ B ₁ − ?
Момент сил М, действующий на стрелку со стороны магнитного поля
М = [ B · P m ], где P m − вектор магнитного момента стрелки.
Модуль момента сил
М = B · P m · sinϕ , где ϕ – угол между векторами B и P m .
При малых колебаниях угол ϕ очень мал и sinϕ ≈ ϕ . Тогда
М = B · P m · ϕ .
При повороте стрелки на угол ϕ возникает момент сил М , стремящийся вернуть стрелку в положение равновесия, т.е. М = — B · P m · ϕ . Если J – момент инерции стрелки относительно оси вращения, то основное уравнение динамики вращательного движения примет вид
Jϕ ’’ = M или Jϕ ’’ = — B · P m · ϕ отсюда
ϕ ’’ + ( B · P m / J ) · ϕ = 0. (1)
Если ω – циклическая частота колебаний, то сравнивая (1) с уравнением гармонических колебаний
ϕ ’’ + ω ² ϕ = 0, получим
ω ² = B · P m / J , отсюда
ω = √( B · P m / J ).
Тогда период T колебаний
T = 2 π / ω или
T = 2 π √( J /( B · P m ) ). (2)
На основе (2) для разных B ₁ и B ₂ получим соответствующие T ₁ и T ₂
T ₁ = 2 π √( J /( B ₁ · P m ) )
T ₂ = 2 π √( J /( B ₂ · P m ) ).
Отсюда
T ₁/ T ₂ = √( B ₂/ B ₁) и отсюда
B ₂/ B ₁ = ( T ₁/ T ₂)² = η ² = 25. Итак
B ₂/ B ₁ = η ² = 25.
Ответ: индукция магнитного поля увеличится в η ² = 25 раз.
4.2-2. Индуктивность катушки равна 0,125 Гн. Уравнение колебаний силы ток в ней имеет вид:
i = 0,4 cos (1000 t ), где все величины выражены в системе СИ. Определить амплитуду напряжения на катушке.
Решение:
L = 0,125 Гн
i = 0,4 cos (1000 t ). (1)
Um − ?
Уравнение колебаний силы тока в катушке имеет вид:
i = Imcos ( ωt ). (2)
Из (1) и (2) имеем
Im = 0,4 А − амплитуда силы тока в катушке; ω = 1000 с⁻¹− частота.
Индуктивное сопротивление катушки: X L = ωL .
По закону Ома
Im = Um / X L , отсюда
Um = X L · Im или
Um = ωL · Im .
Um = 1000·0,125·0,4 = 50 В.
Ответ: Um = 50 В.
4.2-3. Электрический колебательный контур состоял из последовательно соединенных катушки с индуктивностью L = 0,8 Гн и конденсатора емкостью С. Сопротивление катушки и соединительных проводов было равно R = 2000 Ом. После того, как часть витков в катушке замкнулась накоротко, индуктивность ее уменьшилась в n = 7 раз, частота собственных колебаний в контуре возросла в k = 3 раза, а коэффициент затухания этих колебаний не изменился. Определить емкость конденсатора .
Решение:
L = 0,8 Гн
R = 2000 Ом
L ₂ = L / n
n = 7
ω ₂ = kω
k = 3
β = const
C − ?
Коэффициент затуханий β = R /(2 L ).
ω и ω ₂ − начальная и конечная частоты собственных колебаний в контуре, где
ω = √( 1/( LC ) — β ² ) = √( 1/( LC ) — R ²/(4 L ²) );
ω ₂ = √( 1/( L ₂ C ) — β ² ) = √( n /( LC ) — R ²/(4 L ²) ).
Возведём в квадрат равенство ω ₂ = kω , получим ω ₂² = k ² ω ² или
n /( LC ) — R ²/(4 L ²) = k ²( 1/( LC ) — R ²/(4 L ²) ), отсюда
C = 4 L ( k ² — n )/( R ²( k ² — 1) ).
C = 4·0,8·(3² — 7)/( 2000²·(3² — 1) ) = 2·10⁻⁷ Ф.
Ответ: C = 4L(k² — n)/( R²(k² — 1) ) = 2·10⁻⁷ Ф.
4.2-4. Ток в колебательном контуре зависит от времени как I = Imsinω₀t, где Im = 9,0 мА, ω₀ = 4,5·10⁴ с⁻¹. Ёмкость конденсатора С = 0,50 мкФ. Найти индуктивность контура и напряжение на конденсаторе в момент t = 0.
Решение:
I = Imsinω₀t (*)
Im = 9·10⁻³ А
ω₀ = 4,5·10⁴ с⁻¹
С = 0,5·10⁻⁶ Ф
L − ?
U(0) − ?
1). Собственная частота ω₀ колебательного контура
1
L = ––––– . (1)
ω₀²C
2). Закон сохранения энергии в колебательном контуре:
LI²/2 + CU²/2 = LIm²/2
или, с учётом (*),
L(Imsinω₀t)²/2 + CU²/2 = LIm²/2.
Отсюда при t = 0 (т.к. sinω₀0 = 0) получим напряжение U(0) = Um на конденсаторе в момент времени t = 0 ( Um − максимальное напряжение ):
CU²(0) = LIm²
и, подставляя сюда L из (1), получим
Im²
CU²(0) = ––––– или
ω₀²C
Im
U(0) = Um = –––– . (2)
ω₀C
Вычисления по формулам (1) и (2 ):
1
L = –––––––––––––––– = 0,001 Гн = 1 мГн.
(4,5·10⁴)²·0,5·10⁻⁶
9·10⁻³
U(0) = Um = –––––––––––––– = 0,4 В.
4,5·10⁴·0,5·10⁻⁶
4.3. Упругие волны. Акустика.
4.3-1. По шнуру слева направо бежит со скоростью v незатухающая гармоническая волна. При этом поперечное смещение точки О шнура изменяется по закону y = Acos ( ωt ). Как зависит от времени смещение точки шнура, находящейся правее точки О на расстоянии x от нее?
Решение:
y = Acos ( ω ( t — x / v ) ).
Ответ: y = Acos ( ω ( t – x / v ) ).
4.3-2. Уравнение плоской звуковой волны имеет вид ξ = 60 cos (1800 t — 5,3 x ). где ξ – в мкм, t – в секундах, х – в метрах .
Найти:
а) отношение амплитуды смещения частиц среды к длине волны;
б) амплитуду колебаний скорости частиц среды и ее отношение к скорости распространения волны;
в) амплитуду колебаний относительной деформации среды и её связь с амплитудой колебаний скорости частиц среды.
а) Уравнение плоской синусоидальной волны
ξ = Acos(ωt – kx). (2)
Из (1) и (2) следует
A = 60 ·10 ⁻ ⁶ м – амплитуда колебаний частиц среды,
ω = 1800 1/с – циклическая частота,
k = 5,3 1/м – волновое число.
k = 2π/λ, отсюда λ = 2π/k. Тогда
A/λ = A/(2π/k) или
A/λ = Ak/(2π).
A / λ = 60 ·10 ⁻ ⁶ · 5,3/(2 · 3,14) = 5,1 ·10 ⁻ ⁵ .
б) Амплитуда колебаний скорости частиц среды
V m = Aω . (*)
Vm = 60 ·10 ⁻ ⁶ · 1800 = 0,11 м/с. = 11 см/с.
Скорость распространения волны
v = ω / k . (3)
Тогда ( см. (*) )
Vm/v = Aω / ( ω / k ) = A k .
Vm/v = A k .
Vm/v = 60 ·10 ⁻ ⁶ · 5,3 = 3,2 ·10 ⁻ ⁴ .
в) Относительную деформацию среды найдём дифференцируя (2) по х:
∂ ξ/ ∂ x = ( Acos(ωt – kx) )x ʹ = — Aksin (ωt – kx).
Ответ: a) A/λ = 5,1 ·10 ⁻ ⁵ ;
б) Vm = 0,11 м/с, Vm/v = 3,2 ·10 ⁻ ⁴;
в) ( ∂ ξ/ ∂ x)m = 3,2 ·10 ⁻ ⁴, V m = v · (d ξ/dx)m , где v = 340 м/с – скорость волны .
4.3-3. Что такое амплитуда колебаний скорости частиц среды?
Решение:
Объясню на простом примере. В озере на воде поплавок. Бросьте в воду камешек, от него во все стороны пойдут волны. Поплавок колеблется на волнах. Скорость колебаний поплавка − это скорость колебаний частиц среды (воды). Максимальная скорость колебаний поплавка − это амплитуда колебаний скорости частиц среды.
Амплитуда колебаний скорости частиц среды
Vm = Aω ( A — амплитуда, ω — циклическая частота).
Скорость распространения волны
v = ω / k ( k — волновое число).
A , ω , k определяют из общего вида уравнения бегущей плоской синусоидальной волны
ξ = Acos ( ωt – kx ).
4.3-4. Точечный изотропный источник испускает звуковые колебания с частотой ν = 1,45 кГц. На расстоянии r₁ = 5 м от источника амплитуда смещения частиц среды А₁ = 50 мкм, а в точке А, находящейся на расстоянии r₂ = 10 м от источника, амплитуда смещения в η = 3 раза меньше А₁. Найти:
а) коэффициент затухания волны γ;
б) амплитуду колебаний скорости частиц среды в точке А.
Решение:
ν = 1450 Гц
r₁ = 5 м
А₁ = 50·10⁻⁶ м
r₂ = 10 м
А₂ = А₁/η (η = 3) (*)
а) γ − ?
б) Vm − ? (в точке А)
От данного точечного источника распространяются сферические волны. Для однородной поглощающей среды уравнение сферической волны:
(1)
где ξ − смещение частиц среды; ω = 2πν − циклическая частота; k − волновое число.
а). Из (1) выпишем амплитуду A смещения частиц среды (множитель перед косинусом):
A = (A₀/r)·e⁻ᵞʳ.
Отсюда для r = r₁ и r = r₂ получаем амплитуды смещения частиц среды A₁ и A₂ соответственно
A ₁ = ( A ₀ / r ₁ ) · e ⁻ ᵞ r₁ , (**)
A ₂ = ( A ₀ / r ₂ ) · e ⁻ ᵞ r ₂ . (***)
Делим (**) на (***) и, с учётом (*), получаем:
η = ( r ₂ / r ₁ ) · e ᵞ ⁽ r ₂ ⁻ r₁ ⁾ отсюда η r ₁ / r ₂ = e ᵞ ⁽ r ₂ ⁻ r₁ ⁾ , отсюда, по определению логарифма, имеем
ln ( η r ₁ / r ₂ ) = γ( r ₂ — r ₁ ), отсюда
γ = ln(3 · 5 /10 )/(10 — 5 ) ≈ 0,08 м ⁻ ¹ .
б). Для нахождения скорости смещения частиц среды V найдём частную производную по времени t от (1):
V = ∂ ξ / ∂ t = ( A ₀ / r ) · e ⁻ ᵞ ʳ ·( — ω sin ( ω t — kr ) ).
С учётом ω = 2πν, имеем
V = — ( 2 π ν A ₀ /r ) ·e ⁻ ᵞ ʳ ·sin ( ω t-kr ) .
Отсюда амплитуда колебаний скорости частиц среды Vm (множитель перед синусом):
4.3-5. Плоская звуковая волна, частота которой 100 Гц и амплитуда 5 мкм, распространяется со скоростью 300 мс в воздухе, плотность которого равна 1 , 2 кгм ³ . Определить интенсивность волны.
Решение:
ν = 100 Гц
а = 5·10⁻⁶ м
V = 300 мс
ρ = 1,2 кгм³
I − ?
Интенсивность I звуковой волны
I = ρ а² ω ² V /2 и т.к. ω = 2 πν , то
I = ρ а²(2 πν )² V /2.
I = 1,2·(5·10⁻⁶)²·(2·3,14·100)²·300/2 = 1,77·10⁻³ Вт/м².
Ответ: I = 1,77·10⁻³ Вт/м².
4.3-6. Стальная струна длины l = 100 см и диаметра d = 0,50 мм даёт основной тон частоты ν = 256 Гц. Найти силу её натяжения.
Решение:
l = 1 м
d = 0,5·10⁻³ м
ν = 256 Гц
ρ = 7800 кг/м³ (плотность стали)
F − ?
В закреплённой с обоих концов натянутой струне при возбуждении поперечных колебаний устанавливаются стоячие волны. Основной тон частоты ν колебаний струны:
ν = V/2l, отсюда
V = 2lν, (1)
где
− фазовая скорость поперечных волн в струне. Отсюда
F = V²ρ₁ , (2)
где ρ₁ = m/l − линейная плотность струны, m = ρV₀ − масса струны, V₀ = (πd²/4)l = πd²l/4 − объём струны.
Имеем: ρ₁ = ρV₀/l = ρ(πd²l/4)/l = ρπd²/4. Получили
ρ₁ = ρπd²/4. (3)
Подставляя в (2) V из (1) и ρ₁ из (3), получим силу натяжения F струны
F = (2lν)²ρπd²/4, или
F = πρ(lνd)².
F = 3,14·7800· (1·256·0,5·10⁻³)² ≈ 401,3 Н.
Ответ: F = πρ(lνd)² ≈ 401,3 Н.
_______________________________________________________________________________________________
4.4. Электромагнитные волны. Излучение.
4.4-1. Электромагнитная волна с частотой 6 · 10 ¹⁴ Гц распространяется в стекле, показатель преломления которого 1,5. Какова скорость волны в стекле и значение волнового числа?
Решение:
ν = 6 · 10¹⁴ Гц
n = 1,5
c = 3 · 10⁸ м/с (скорость света в вакууме)
V – ? k – ?
Скорость V волны в стекле:
V = c / n . (1)
Длина волны в стекле:
λ = V / ν = c /( nν ). (*)
Волновое число k:
k = 2 π / λ или с учётом (*)
k = 2 πnν /с. (2)
Вычисления по (1), (2)
V = 3 · 10⁸/1,5 = 2 · 10⁸ м/с.
k = 2 · 3,14 · 1,5 · 6 · 10¹⁴/(3 · 10⁸) = 1,88 · 10⁷ (1/м).
Ответ: V = 2 · 10⁸ м/с; k = 1,88 · 10⁷ (1/м).
4.4-2. Определить показатель преломления призмы из парафина , если его диэлектрическая проницаемость Ԑ = 2 и магнитная проницаемость μ = 1.
Решение:
Ԑ = 2
μ = 1
n – ?
Показатель преломления среды
n = C / V . (1)
С – скорость света в вакууме.
Скорость света в среде
V = C /√( Ԑμ ). (2)
Из (1) и (2) имеем
n = √( Ԑμ ).
n = √(2·1) = 1,41.
Ответ: n = 1,41.
___________________________________________________________________________________
🎥 Видео
Физика 11 класс (Урок№2 - Механические волны.)Скачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

10й класс; Физика; "Уравнение плоской волны"Скачать

Распространение звука. Звуковые волны | Физика 9 класс #32 | ИнфоурокСкачать

Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Д.А. Гаджиев. Взаимодействие плоской звуковой волны с квазипотенциальным вихремСкачать

5.6 Механические волны. Виды волнСкачать
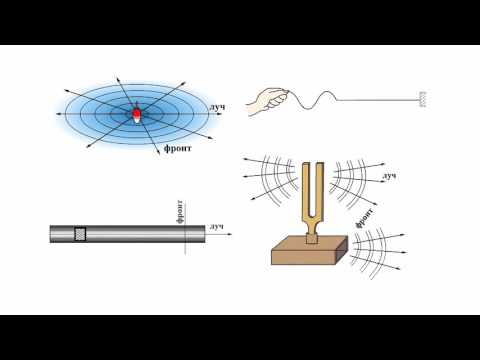
Движение вязкой жидкости. Уравнения динамики сплошной среды. Звуковая волна. Лекция 15Скачать

Распространение волн в упругих средах. Звуковые волны | Физика 11 класс #18 | ИнфоурокСкачать

Получение уравнения плоской бегущей волны.Скачать

74. Упругие волныСкачать

Физика 9 класс. §32 Распространение звука. Звуковые волны.Скачать

Физика 9 класс (Урок№15 - Звуковые волны. Скорость звука.)Скачать

Волны. Основные понятия. Решение задач.Задача 1Скачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать

Механические модели волн. 1.Скачать

ЗВУКОВЫЕ ВОЛНЫ + решение задач | 9 класс физика ПерышкинСкачать

4.3 Плоские электромагнитные волны в идеальных диэлектрических средахСкачать



.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
%20%D0%A4%D0%98%D0%97.jpg)
%20%D0%A4%D0%98%D0%97.jpg)
%20%D0%A4%D0%98%D0%97.jpg)



.jpg)