Площадь поверхности вращения кривой заданной параметрическими уравнениями (5 видео)

Как найти площадь поверхности вращения с помощью интеграла

Прежде чем перейти к формулам площади поверхности вращения, дадим краткую формулировку самой поверхности вращения. Поверхность вращения, или, что то же самое — поверхность тела вращения — пространственная фигура, образованная вращением отрезка AB кривой вокруг оси Ox (рисунок ниже).

Представим себе криволинейную трапецию, ограниченную сверху упомянутым отрезком кривой. Тело, образованное вращением этой трапеции вокруг то же оси Ox, и есть тело вращения. А площадь поверхности вращения или поверхности тела вращения — это его внешняя оболочка, не считая кругов, образованных вращением вокруг оси прямых x = a и x = b .

Заметим, что тело вращения и соответственно его поверхность могут быть образованы также вращением фигуры не вокруг оси Ox, а вокруг оси Oy.

Содержание

Вычисление площади поверхности вращения, заданной в прямоугольных координатах
Вычисление площади поверхности вращения, заданной параметрически
Вычисление площади поверхности вращения, заданной в полярных координатах
Площадь поверхности вращения кривой заданной параметрическими уравнениями
Контакты
Вычисление площади фигуры, ограниченной параметрически заданной кривой
Основная формула для вычисления
Решение задач на вычисление площади фигуры, которая ограничена параметрически заданной кривой
🔥 Видео

Видео:Площадь поверхности вращения.Скачать

Вычисление площади поверхности вращения, заданной в прямоугольных координатах

Пусть в прямоугольных координатах на плоскости уравнением y = f(x) задана кривая, вращением которой вокруг координатной оси образовано тело вращения.

Формула для вычисления площади поверхности вращения следующая:

(1).

Пример 1. Найти площадь поверхности параболоида, образованную вращением вокруг оси Ox дуги параболы , соответствующей изменению x от x = 0 до x = a .

Решение. Выразим явно функцию, которая задаёт дугу параболы:

Найдём производную этой функции:

Прежде чем воспользоваться формулу для нахождения площади поверхности вращения, напишем ту часть её подынтегрального выражения, которая представляет собой корень и подставим туда найденную только что производную:

Далее по формуле (1) находим:

Ответ: длина дуги кривой равна

Пример 2. Найти площадь поверхности, образуемой вращением вокруг оси Ox астроиды .

Решение. Достаточно вычислить площадь поверхности, получающейся от вращения одной ветви астроиды, расположенной в первой четверти, и умножить её на 2. Из уравнения астроиды выразим явно функцию, которую нам нужно будет подставить в формулу для нахождения площади повержности вращения:

Производим интегрирование от 0 до a:

Ответ: площадь поверхности вращения равна .

Видео:Площадь эллипсоида + вывод формулы площади поверхности вращенияСкачать

Вычисление площади поверхности вращения, заданной параметрически

Рассмотрим случай, когда кривая, образующая поверхность вращения, задана параметрическими уравнениями

Тогда площадь поверхности вращения вычисляется по формуле

(2).

Пример 3. Найти площадь поверхности вращения, образованной вращением вокруг оси Oy фигуры, ограниченной циклоидой и прямой y = a . Циклоида задана параметрическими уравнениями

Решение. Найдём точки пересечения циклоиды и прямой. Приравнивая уравнение циклоиды и уравнение прямой y = a , найдём

Из этого следует, что границы интегрирования соответствуют

Теперь можем применить формулу (2). Найдём производные:

Запишем подкоренное выражение в формуле, подставляя найденные производные:

Найдём корень из этого выражения:

Подставим найденное в формулу (2):

И, наконец, находим

В преобразовании выражений были использованы тригонометрические формулы

Ответ: площадь поверхности вращения равна .

Видео:Площадь поверхности вращенияСкачать

Вычисление площади поверхности вращения, заданной в полярных координатах

Пусть кривая, вращением которой образована поверхность, задана в полярных координатах:

Площадь поверхности вращения вычисляется по формуле:

(3).

Пример 4. Найти площадь поверхности, образованной вращением лемнискаты вокруг полярной оси.

Решение. Действительные значения для ρ получаются при , то есть при (правая ветвь лемнискаты) или при (левая ветвь лемнискаты).

Решение. Дифференциал корня из формулы площади поверхности вращения равен:

В свою очередь произведение функции, которой задана лемниската, на синус угла равно

Поэтому площадь поверхности вращения найдём следующим образом:

Видео:Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать

Площадь поверхности вращения кривой заданной параметрическими уравнениями

Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Видео:Вычисление площади поверхности вращения и разбор задач.Скачать

Вычисление площади фигуры, ограниченной параметрически заданной кривой

Когда мы выясняли геометрический смысл определенного интеграла, у нас получилась формула, с помощью которой можно найти площадь криволинейной трапеции, ограниченной осью абсцисс, прямыми x = a , x = b , а также непрерывной (неотрицательной или неположительной) функцией y = f ( x ) . Иногда удобнее задавать функцию, ограничивающую фигуру, в параметрическом виде, т.е. выражать функциональную зависимость через параметр t . В рамках данного материала мы покажем, как можно найти площадь фигуры, если она ограничена параметрически заданной кривой.

После объяснения теории и выведения формулы мы разберем несколько характерных примеров на нахождение площади таких фигур.

Видео:§64 Поверхности вращенияСкачать

Основная формула для вычисления

Допустим, что у нас имеется криволинейная трапеция, границами которой являются прямые x = a , x = b , ось O x и параметрически заданная кривая x = φ ( t ) y = ψ ( t ) , а функции x = φ ( t ) и y = ψ ( t ) являются непрерывными на интервале α ; β , α β , x = φ ( t ) будет непрерывно возрастать на нем и φ ( α ) = a , φ ( β ) = b .

Чтобы вычислить площадь трапеции при таких условиях, нужно использовать формулу S ( G ) = ∫ α β ψ ( t ) · φ ‘ ( t ) d t .

Мы вывели ее из формулы площади криволинейной трапеции S ( G ) = ∫ a b f ( x ) d x методом подстановки x = φ ( t ) y = ψ ( t ) :

S ( G ) = ∫ a b f ( x ) d x = ∫ α β ψ ( t ) d ( φ ( t ) ) = ∫ α β ψ ( t ) · φ ‘ ( t ) d t

Учитывая монотонное убывание функции x = φ ( t ) на интервале β ; α , β α , нужная формула принимает вид S ( G ) = — ∫ β α ψ ( t ) · φ ‘ ( t ) d t .

Если функция x = φ ( t ) не относится к основным элементарным, то нам понадобится вспомнить основные правила возрастания и убывания функции на интервале, чтобы определить, будет ли она возрастающей или убывающей.

Видео:Нахождение площади поверхности вращения телаСкачать

Решение задач на вычисление площади фигуры, которая ограничена параметрически заданной кривой

В этом пункте мы разберем несколько задач на применение формулы, выведенной выше.

Условие: найдите площадь фигуры, которую образует линия, заданная уравнениями вида x = 2 cos t y = 3 sin t .

Решение

У нас есть параметрически заданная линия. Графически ее можно отобразить в виде эллипса с двумя полуосями 2 и 3 . См на иллюстрацию:

Попробуем найти площадь 1 4 полученной фигуры, которая занимает первый квадрант. Область находится в интервале x ∈ a ; b = 0 ; 2 . Далее умножим полученное значение на 4 и найдем площадь целой фигуры.

Вот ход наших вычислений:

x = φ ( t ) = 2 cos t y = ψ ( t ) = 3 sin t φ α = a ⇔ 2 cos α = 0 ⇔ α = π 2 + πk , k ∈ Z , φ β = b ⇔ 2 cos β = 2 ⇔ β = 2 πk , k ∈ Z

При k , равном 0 , мы получим интервал β ; α = 0 ; π 2 . Функция x = φ ( t ) = 2 cos t на нем будет монотонно убывать (подробнее см. статью об основных элементарных функциях и их свойствах). Значит, можно применить формулу вычисления площади и найти определенный интеграл, используя формулу Ньютона-Лейбница:

— ∫ 0 π 2 3 sin t · 2 cos t ‘ d t = 6 ∫ 0 π 2 sin 2 t d t = 3 ∫ 0 π 2 ( 1 — cos ( 2 t ) d t = = 3 · t — sin ( 2 t ) 2 0 π 2 = 3 · π 2 — sin 2 · π 2 2 — 0 — sin 2 · 0 2 = 3 π 2

Значит, площадь фигуры, заданной исходной кривой, будет равна S ( G ) = 4 · 3 π 2 = 6 π .

Ответ: S ( G ) = 6 π

Уточним, что при решении задачи выше можно было взять не только четверть эллипса, но и его половину – верхнюю или нижнюю. Одна половина будет расположена на интервале x ∈ a ; b = — 2 ; 2 . В этом случае у нас бы получилось:

φ ( α ) = a ⇔ 2 cos α = — 2 ⇔ α = π + π k , k ∈ Z , φ ( β ) = b ⇔ 2 cos β = 2 ⇔ β = 2 π k , k ∈ Z

Таким образом, при k равном 0 , мы получили β ; α = 0 ; π . Функция x = φ ( t ) = 2 cos t на этом интервале будет монотонно убывать.

После этого вычисляем площадь половины эллипса:

— ∫ 0 π 3 sin t · 2 cos t ‘ d t = 6 ∫ 0 π sin 2 t d t = 3 ∫ 0 π ( 1 — cos ( 2 t ) d t = = 3 · t — sin ( 2 t ) 2 0 π = 3 · π — sin 2 · π 2 — 0 — sin 2 · 0 2 = 3 π

Важно отметить, что можно взять только верхнюю или нижнюю часть, а правую или левую нельзя.

Можно составить параметрическое уравнение данного эллипса, центр которого будет расположен в начале координат. Оно будет иметь вид x = a · cos t y = b · sin t . Действуя так же, как и в примере выше, получим формулу для вычисления площади эллипса S э л и п с а = πab .

Задать окружность, центр которой расположен в начале координат, можно с помощью уравнения x = R · cos t y = R · sin t , где t является параметром, а R – радиусом данной окружности. Если мы сразу воспользуемся формулой площади эллипса, то то у нас получится формула, с помощью которой можно вычислить площадь круга с радиусом R : S к р у г а = πR 2 .

Разберем еще одну задачу.

Условие: найдите, чему будет равна площадь фигуры, которая ограничена параметрически заданной кривой x = 3 cos 3 t y = 2 sin 3 t .

Решение

Сразу уточним, что данная кривая имеет вид вытянутой астроиды. Обычно астроида выражается с помощью уравнения вида x = a · cos 3 t y = a · sin 3 t .

Теперь разберем подробно, как построить такую кривую. Выполним построение по отдельным точкам. Это самый распространенный метод, который применим для большинства задач. Более сложные примеры требуют проведения дифференциального исчисления, чтобы выявить параметрически заданную функцию.

У нас x = φ ( t ) = 3 cos 3 t , y = ψ ( t ) = 2 sin 3 t .

Данные функции являются определенными для всех действительных значений t . Для sin и cos известно, что они являются периодическими и их период составляет 2 пи. Вычислив значения функций x = φ ( t ) = 3 cos 3 t , y = ψ ( t ) = 2 sin 3 t для некоторых t = t 0 ∈ 0 ; 2 π π 8 , π 4 , 3 π 8 , π 2 , . . . , 15 π 8 , получим точки x 0 ; y 0 = ( φ ( t 0 ) ; ψ ( t 0 ) ) .

Составим таблицу итоговых значений:

Площадь поверхности вращения кривой заданной параметрическими уравнениями

t 0	0	π 8	π 4	3 π 8	π 2	5 π 8	3 π 4	7 π 8	π
x 0 = φ ( t 0 )	3	2 . 36	1 . 06	0 . 16	0	— 0 . 16	— 1 . 06	— 2 . 36	— 3
y 0 = ψ ( t 0 )	0	0 . 11	0 . 70	1 . 57	2	1 . 57	0 . 70	0 . 11	0

t 0	9 π 8	5 π 4	11 π 8	3 π 2	13 π 8	7 π 4	15 π 8	2 π
x 0 = φ ( t 0 )	— 2 . 36	— 1 . 06	— 0 . 16	0	0 . 16	1 . 06	2 . 36	3
y 0 = ψ ( t 0 )	— 0 . 11	— 0 . 70	— 1 . 57	— 2	— 1 . 57	— 0 . 70	— 0 . 11	0

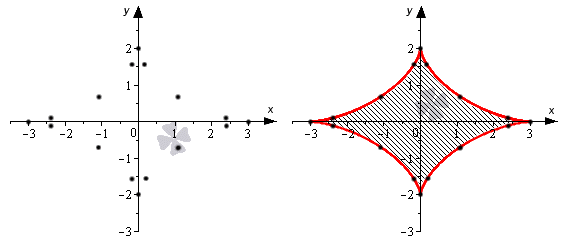
После этого отметим нужные точки на плоскости и соединим их одной линией.

Теперь нам надо найти площадь той части фигуры, что находится в первой координатной четверти. Для нее x ∈ a ; b = 0 ; 3 :

φ ( α ) = a ⇔ 3 cos 3 t = 0 ⇔ α = π 2 + πk , k ∈ Z , φ ( β ) = b ⇔ 3 cos 3 t = 3 ⇔ β = 2 πk , k ∈ Z

Если k равен 0 , то у нас получится интервал β ; α = 0 ; π 2 , и функция x = φ ( t ) = 3 cos 3 t на нем будет монотонно убывать. Теперь берем формулу площади и считаем:

— ∫ 0 π 2 2 sin 3 t · 3 cos 3 t ‘ d t = 18 ∫ 0 π 2 sin 4 t · cos 2 t d t = = 18 ∫ 0 π 2 sin 4 t · ( 1 — sin 2 t ) d t = 18 ∫ 0 π 2 sin 4 t d t — ∫ 0 π 2 sin 6 t d t

У нас получились определенные интегралы, которые можно вычислить с помощью формулы Ньютона-Лейбница. Первообразные для этой формулы можно найти, используя рекуррентную формулу J n ( x ) = — cos x · sin n — 1 ( x ) n + n — 1 n J n — 2 ( x ) , где J n ( x ) = ∫ sin n x d x .

∫ sin 4 t d t = — cos t · sin 3 t 4 + 3 4 ∫ sin 2 t d t = = — cos t · sin 3 t 4 + 3 4 — cos t · sin t 2 + 1 2 ∫ sin 0 t d t = = — cos t · sin 3 t 4 — 3 cos t · sin t 8 + 3 8 t + C ⇒ ∫ 0 π 2 sin 4 t d t = — cos t · sin 3 t 4 — 3 cos t · sin t 8 + 3 8 t 0 π 2 = 3 π 16 ∫ sin 6 t d t = — cos t · sin 5 t 6 + 5 6 ∫ sin 4 t d t ⇒ ∫ 0 π 2 sin 6 t d t = — cos t · sin 5 t 6 0 π 2 + 5 6 ∫ 0 π 2 sin 4 t d t = 5 6 · 3 π 16 = 15 π 96

Мы вычислили площадь четверти фигуры. Она равна 18 ∫ 0 π 2 sin 4 t d t — ∫ 0 π 2 sin 6 t d t = 18 3 π 16 — 15 π 96 = 9 π 16 .

Если мы умножим это значение на 4 , получим площадь всей фигуры – 9 π 4 .

Точно таким же образом мы можем доказать, что площадь астроиды, заданной уравнениями x = a · cos 3 t y = a · sin 3 t , можно найти по формуле S а с т р о и д ы = 3 πa 2 8 , а площадь фигуры, которая ограничена линией x = a · cos 3 t y = b · sin 3 t , считается по формуле S = 3 πab 8 .