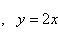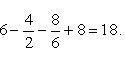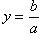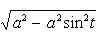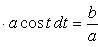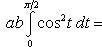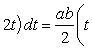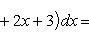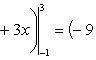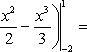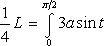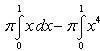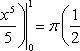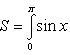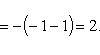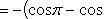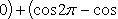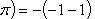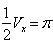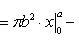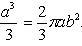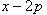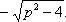В предыдущем разделе, посвященном разбору геометрического смысла определенного интеграла, мы получили ряд формул для вычисления площади криволинейной трапеции:
S ( G ) = ∫ a b f ( x ) d x для непрерывной и неотрицательной функции y = f ( x ) на отрезке [ a ; b ] ,
S ( G ) = — ∫ a b f ( x ) d x для непрерывной и неположительной функции y = f ( x ) на отрезке [ a ; b ] .
Эти формулы применимы для решения относительно простых задач. На деле же нам чаще придется работать с более сложными фигурами. В связи с этим, данный раздел мы посвятим разбору алгоритмов вычисления площади фигур, которые ограничены функциями в явном виде, т.е. как y = f ( x ) или x = g ( y ) .
- Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
- Примеры вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
- Итоги
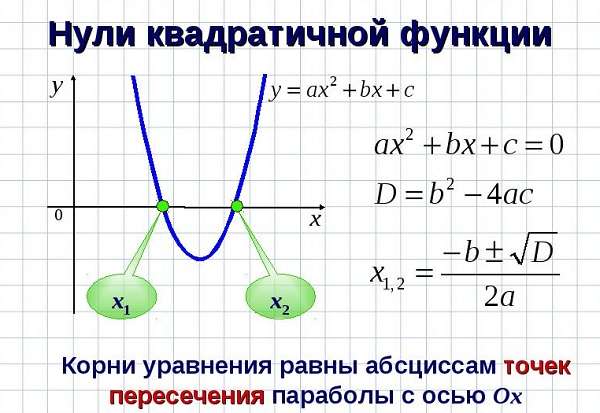
- Как построить параболу? Что такое парабола? Как решаются квадратные уравнения?
- ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
- ПРАКТИЧЕСКАЯ ЧАСТЬ
- Парабола свойства и график квадратичной функции
- Что такое парабола и как она выглядит
- Каноническое уравнение параболы
- Свойства и график квадратичной функции
- Как определить, куда направлены ветви параболы
- Как найти вершину параболы по формуле
- Смещение параболы
- Как строить параболу по квадратному уравнению
- Директриса, эксцентриситет, фокус параболы
- Заключение
- 🌟 Видео
Видео:Как определить уравнение параболы по графику?Скачать

Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
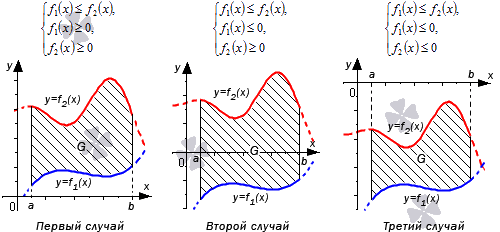
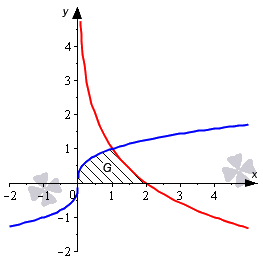
Пусть функции y = f 1 ( x ) и y = f 2 ( x ) определены и непрерывны на отрезке [ a ; b ] , причем f 1 ( x ) ≤ f 2 ( x ) для любого значения x из [ a ; b ] . Тогда формула для вычисления площади фигуры G , ограниченной линиями x = a , x = b , y = f 1 ( x ) и y = f 2 ( x ) будет иметь вид S ( G ) = ∫ a b f 2 ( x ) — f 1 ( x ) d x .
Похожая формула будет применима для площади фигуры, ограниченной линиями y = c , y = d , x = g 1 ( y ) и x = g 2 ( y ) : S ( G ) = ∫ c d ( g 2 ( y ) — g 1 ( y ) d y .
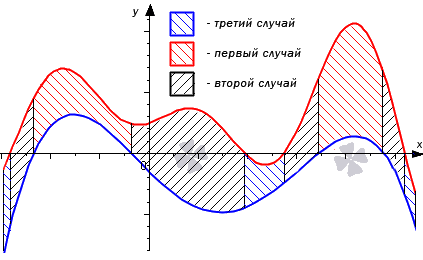
Разберем три случая, для которых формула будет справедлива.
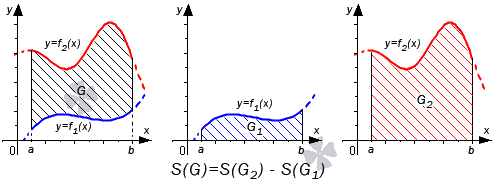
В первом случае, учитывая свойство аддитивности площади, сумма площадей исходной фигуры G и криволинейной трапеции G 1 равна площади фигуры G 2 . Это значит, что
Поэтому, S ( G ) = S ( G 2 ) — S ( G 1 ) = ∫ a b f 2 ( x ) d x — ∫ a b f 1 ( x ) d x = ∫ a b ( f 2 ( x ) — f 1 ( x ) ) d x .
Выполнить последний переход мы можем с использованием третьего свойства определенного интеграла.
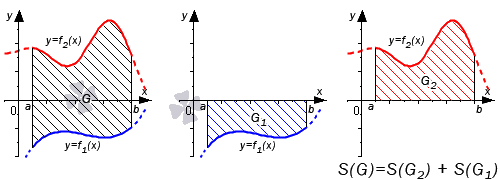
Во втором случае справедливо равенство: S ( G ) = S ( G 2 ) + S ( G 1 ) = ∫ a b f 2 ( x ) d x + — ∫ a b f 1 ( x ) d x = ∫ a b ( f 2 ( x ) — f 1 ( x ) ) d x
Графическая иллюстрация будет иметь вид:
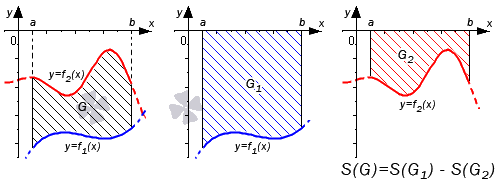
Если обе функции неположительные, получаем: S ( G ) = S ( G 2 ) — S ( G 1 ) = — ∫ a b f 2 ( x ) d x — — ∫ a b f 1 ( x ) d x = ∫ a b ( f 2 ( x ) — f 1 ( x ) ) d x . Графическая иллюстрация будет иметь вид:
Перейдем к рассмотрению общего случая, когда y = f 1 ( x ) и y = f 2 ( x ) пересекают ось O x .
Точки пересечения мы обозначим как x i , i = 1 , 2 , . . . , n — 1 . Эти точки разбивают отрезок [ a ; b ] на n частей x i — 1 ; x i , i = 1 , 2 , . . . , n , где α = x 0 x 1 x 2 . . . x n — 1 x n = b . Фигуру G можно представить объединением фигур G i , i = 1 , 2 , . . . , n . Очевидно, что на своем интервале G i попадает под один из трех рассмотренных ранее случаев, поэтому их площади находятся как S ( G i ) = ∫ x i — 1 x i ( f 2 ( x ) — f 1 ( x ) ) d x , i = 1 , 2 , . . . , n
S ( G ) = ∑ i = 1 n S ( G i ) = ∑ i = 1 n ∫ x i x i f 2 ( x ) — f 1 ( x ) ) d x = = ∫ x 0 x n ( f 2 ( x ) — f ( x ) ) d x = ∫ a b f 2 ( x ) — f 1 ( x ) d x
Последний переход мы можем осуществить с использованием пятого свойства определенного интеграла.
Проиллюстрируем на графике общий случай.
Формулу S ( G ) = ∫ a b f 2 ( x ) — f 1 ( x ) d x можно считать доказанной.
А теперь перейдем к разбору примеров вычисления площади фигур, которые ограничены линиями y = f ( x ) и x = g ( y ) .
Видео:Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать

Примеры вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
Рассмотрение любого из примеров мы будем начинать с построения графика. Изображение позволит нам представлять сложные фигуры как объединения более простых фигур. Если построение графиков и фигур на них вызывает у вас затруднения, можете изучить раздел об основных элементарных функциях, геометрическом преобразовании графиков функций, а также построению графиков во время исследования функции.
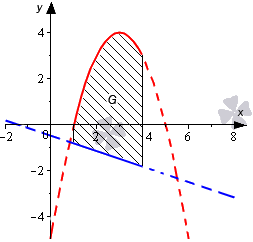
Необходимо определить площадь фигуры, которая ограничена параболой y = — x 2 + 6 x — 5 и прямыми линиями y = — 1 3 x — 1 2 , x = 1 , x = 4 .
Решение
Изобразим линии на графике в декартовой системе координат.
На отрезке [ 1 ; 4 ] график параболы y = — x 2 + 6 x — 5 расположен выше прямой y = — 1 3 x — 1 2 . В связи с этим, для получения ответа используем формулу, полученную ранее, а также способ вычисления определенного интеграла по формуле Ньютона-Лейбница:
S ( G ) = ∫ 1 4 — x 2 + 6 x — 5 — — 1 3 x — 1 2 d x = = ∫ 1 4 — x 2 + 19 3 x — 9 2 d x = — 1 3 x 3 + 19 6 x 2 — 9 2 x 1 4 = = — 1 3 · 4 3 + 19 6 · 4 2 — 9 2 · 4 — — 1 3 · 1 3 + 19 6 · 1 2 — 9 2 · 1 = = — 64 3 + 152 3 — 18 + 1 3 — 19 6 + 9 2 = 13
Ответ: S ( G ) = 13
Рассмотрим более сложный пример.
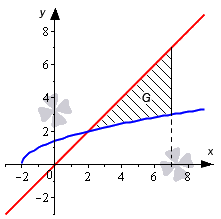
Необходимо вычислить площадь фигуры, которая ограничена линиями y = x + 2 , y = x , x = 7 .
Решение
В данном случае мы имеем только одну прямую линию, расположенную параллельно оси абсцисс. Это x = 7 . Это требует от нас найти второй предел интегрирования самостоятельно.
Построим график и нанесем на него линии, данные в условии задачи.
Имея график перед глазами, мы легко можем определить, что нижним пределом интегрирования будет абсцисса точки пересечения графика прямой y = x и полу параболы y = x + 2 . Для нахождения абсциссы используем равенства:
y = x + 2 О Д З : x ≥ — 2 x 2 = x + 2 2 x 2 — x — 2 = 0 D = ( — 1 ) 2 — 4 · 1 · ( — 2 ) = 9 x 1 = 1 + 9 2 = 2 ∈ О Д З x 2 = 1 — 9 2 = — 1 ∉ О Д З
Получается, что абсциссой точки пересечения является x = 2 .
Обращаем ваше внимание на тот факт, что в общем примере на чертеже линии y = x + 2 , y = x пересекаются в точке ( 2 ; 2 ) , поэтому такие подробные вычисления могут показаться излишними. Мы привели здесь такое подробное решение только потому, что в более сложных случаях решение может быть не таким очевидным. Это значит, что координаты пересечения линий лучше всегда вычислять аналитически.
На интервале [ 2 ; 7 ] график функции y = x расположен выше графика функции y = x + 2 . Применим формулу для вычисления площади:
S ( G ) = ∫ 2 7 ( x — x + 2 ) d x = x 2 2 — 2 3 · ( x + 2 ) 3 2 2 7 = = 7 2 2 — 2 3 · ( 7 + 2 ) 3 2 — 2 2 2 — 2 3 · 2 + 2 3 2 = = 49 2 — 18 — 2 + 16 3 = 59 6
Ответ: S ( G ) = 59 6
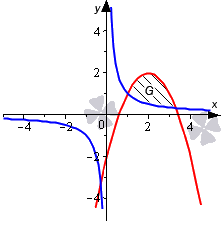
Необходимо вычислить площадь фигуры, которая ограничена графиками функций y = 1 x и y = — x 2 + 4 x — 2 .
Решение
Нанесем линии на график.
Определимся с пределами интегрирования. Для этого определим координаты точек пересечения линий, приравняв выражения 1 x и — x 2 + 4 x — 2 . При условии, что x не равно нулю, равенство 1 x = — x 2 + 4 x — 2 становится эквивалентным уравнению третьей степени — x 3 + 4 x 2 — 2 x — 1 = 0 с целыми коэффициентами. Освежить в памяти алгоритм по решению таких уравнений мы можете, обратившись к разделу «Решение кубических уравнений».
Корнем этого уравнения является х = 1 : — 1 3 + 4 · 1 2 — 2 · 1 — 1 = 0 .
Разделив выражение — x 3 + 4 x 2 — 2 x — 1 на двучлен x — 1 , получаем: — x 3 + 4 x 2 — 2 x — 1 ⇔ — ( x — 1 ) ( x 2 — 3 x — 1 ) = 0
Оставшиеся корни мы можем найти из уравнения x 2 — 3 x — 1 = 0 :
x 2 — 3 x — 1 = 0 D = ( — 3 ) 2 — 4 · 1 · ( — 1 ) = 13 x 1 = 3 + 13 2 ≈ 3 . 3 ; x 2 = 3 — 13 2 ≈ — 0 . 3
Мы нашли интервал x ∈ 1 ; 3 + 13 2 , на котором фигура G заключена выше синей и ниже красной линии. Это помогает нам определить площадь фигуры:
S ( G ) = ∫ 1 3 + 13 2 — x 2 + 4 x — 2 — 1 x d x = — x 3 3 + 2 x 2 — 2 x — ln x 1 3 + 13 2 = = — 3 + 13 2 3 3 + 2 · 3 + 13 2 2 — 2 · 3 + 13 2 — ln 3 + 13 2 — — — 1 3 3 + 2 · 1 2 — 2 · 1 — ln 1 = 7 + 13 3 — ln 3 + 13 2
Ответ: S ( G ) = 7 + 13 3 — ln 3 + 13 2
Необходимо вычислить площадь фигуры, которая ограничена кривыми y = x 3 , y = — log 2 x + 1 и осью абсцисс.
Решение
Нанесем все линии на график. Мы можем получить график функции y = — log 2 x + 1 из графика y = log 2 x , если расположим его симметрично относительно оси абсцисс и поднимем на одну единицу вверх. Уравнение оси абсцисс у = 0 .
Обозначим точки пересечения линий.
Как видно из рисунка, графики функций y = x 3 и y = 0 пересекаются в точке ( 0 ; 0 ) . Так получается потому, что х = 0 является единственным действительным корнем уравнения x 3 = 0 .
x = 2 является единственным корнем уравнения — log 2 x + 1 = 0 , поэтому графики функций y = — log 2 x + 1 и y = 0 пересекаются в точке ( 2 ; 0 ) .
x = 1 является единственным корнем уравнения x 3 = — log 2 x + 1 . В связи с этим графики функций y = x 3 и y = — log 2 x + 1 пересекаются в точке ( 1 ; 1 ) . Последнее утверждение может быть неочевидным, но уравнение x 3 = — log 2 x + 1 не может иметь более одного корня, так как функция y = x 3 является строго возрастающей, а функция y = — log 2 x + 1 строго убывающей.
Дальнейшее решение предполагает несколько вариантов.
Вариант №1
Фигуру G мы можем представить как сумму двух криволинейных трапеций, расположенных выше оси абсцисс, первая из которых располагается ниже средней линии на отрезке x ∈ 0 ; 1 , а вторая ниже красной линии на отрезке x ∈ 1 ; 2 . Это значит, что площадь будет равна S ( G ) = ∫ 0 1 x 3 d x + ∫ 1 2 ( — log 2 x + 1 ) d x .
Вариант №2
Фигуру G можно представить как разность двух фигур, первая из которых расположена выше оси абсцисс и ниже синей линии на отрезке x ∈ 0 ; 2 , а вторая между красной и синей линиями на отрезке x ∈ 1 ; 2 . Это позволяет нам найти площадь следующим образом:
S ( G ) = ∫ 0 2 x 3 d x — ∫ 1 2 x 3 — ( — log 2 x + 1 ) d x
В этом случае для нахождения площади придется использовать формулу вида S ( G ) = ∫ c d ( g 2 ( y ) — g 1 ( y ) ) d y . Фактически, линии, которые ограничивают фигуру, можно представить в виде функций от аргумента y .
Разрешим уравнения y = x 3 и — log 2 x + 1 относительно x :
y = x 3 ⇒ x = y 3 y = — log 2 x + 1 ⇒ log 2 x = 1 — y ⇒ x = 2 1 — y
Получим искомую площадь:
S ( G ) = ∫ 0 1 ( 2 1 — y — y 3 ) d y = — 2 1 — y ln 2 — y 4 4 0 1 = = — 2 1 — 1 ln 2 — 1 4 4 — — 2 1 — 0 ln 2 — 0 4 4 = — 1 ln 2 — 1 4 + 2 ln 2 = 1 ln 2 — 1 4
Ответ: S ( G ) = 1 ln 2 — 1 4
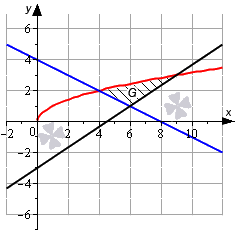
Необходимо вычислить площадь фигуры, которая ограничена линиями y = x , y = 2 3 x — 3 , y = — 1 2 x + 4 .
Решение
Красной линией нанесем на график линию, заданную функцией y = x . Синим цветом нанесем линию y = — 1 2 x + 4 , черным цветом обозначим линию y = 2 3 x — 3 .
Отметим точки пересечения.
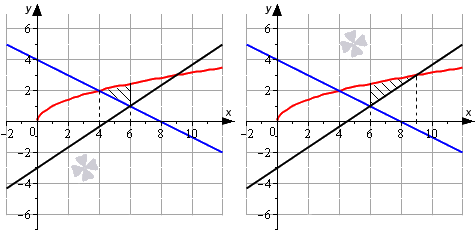
Найдем точки пересечения графиков функций y = x и y = — 1 2 x + 4 :
x = — 1 2 x + 4 О Д З : x ≥ 0 x = — 1 2 x + 4 2 ⇒ x = 1 4 x 2 — 4 x + 16 ⇔ x 2 — 20 x + 64 = 0 D = ( — 20 ) 2 — 4 · 1 · 64 = 144 x 1 = 20 + 144 2 = 16 ; x 2 = 20 — 144 2 = 4 П р о в е р к а : x 1 = 16 = 4 , — 1 2 x 1 + 4 = — 1 2 · 16 + 4 = — 4 ⇒ x 1 = 16 н е я в л я е т с я р е ш е н и е м у р а в н е н и я x 2 = 4 = 2 , — 1 2 x 2 + 4 = — 1 2 · 4 + 4 = 2 ⇒ x 2 = 4 я в л я е т с я р е ш е н и е м у р а в н и н и я ⇒ ( 4 ; 2 ) т о ч к а п е р е с е ч е н и я y = x и y = — 1 2 x + 4
Найдем точку пересечения графиков функций y = x и y = 2 3 x — 3 :
x = 2 3 x — 3 О Д З : x ≥ 0 x = 2 3 x — 3 2 ⇔ x = 4 9 x 2 — 4 x + 9 ⇔ 4 x 2 — 45 x + 81 = 0 D = ( — 45 ) 2 — 4 · 4 · 81 = 729 x 1 = 45 + 729 8 = 9 , x 2 45 — 729 8 = 9 4 П р о в е р к а : x 1 = 9 = 3 , 2 3 x 1 — 3 = 2 3 · 9 — 3 = 3 ⇒ x 1 = 9 я в л я е т с я р е ш е н и е м у р а в н е н и я ⇒ ( 9 ; 3 ) т о ч к а п е р е с е ч а н и я y = x и y = 2 3 x — 3 x 2 = 9 4 = 3 2 , 2 3 x 1 — 3 = 2 3 · 9 4 — 3 = — 3 2 ⇒ x 2 = 9 4 н е я в л я е т с я р е ш е н и е м у р а в н е н и я
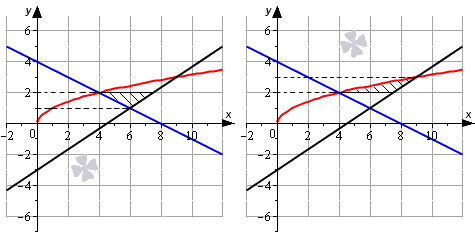
Найдем точку пересечения линий y = — 1 2 x + 4 и y = 2 3 x — 3 :
— 1 2 x + 4 = 2 3 x — 3 ⇔ — 3 x + 24 = 4 x — 18 ⇔ 7 x = 42 ⇔ x = 6 — 1 2 · 6 + 4 = 2 3 · 6 — 3 = 1 ⇒ ( 6 ; 1 ) т о ч к а п е р е с е ч е н и я y = — 1 2 x + 4 и y = 2 3 x — 3
Дальше мы можем продолжить вычисления двумя способами.
Способ №1
Представим площадь искомой фигуры как сумму площадей отдельных фигур.
Тогда площадь фигуры равна:
S ( G ) = ∫ 4 6 x — — 1 2 x + 4 d x + ∫ 6 9 x — 2 3 x — 3 d x = = 2 3 x 3 2 + x 2 4 — 4 x 4 6 + 2 3 x 3 2 — x 2 3 + 3 x 6 9 = = 2 3 · 6 3 2 + 6 2 4 — 4 · 6 — 2 3 · 4 3 2 + 4 2 4 — 4 · 4 + + 2 3 · 9 3 2 — 9 2 3 + 3 · 9 — 2 3 · 6 3 2 — 6 2 3 + 3 · 6 = = — 25 3 + 4 6 + — 4 6 + 12 = 11 3
Способ №2
Площадь исходной фигуры можно представить как сумму двух других фигур.
Тогда решим уравнение линии относительно x , а только после этого применим формулу вычисления площади фигуры.
y = x ⇒ x = y 2 к р а с н а я л и н и я y = 2 3 x — 3 ⇒ x = 3 2 y + 9 2 ч е р н а я л и н и я y = — 1 2 x + 4 ⇒ x = — 2 y + 8 с и н я я л и н и я
Таким образом, площадь равна:
S ( G ) = ∫ 1 2 3 2 y + 9 2 — — 2 y + 8 d y + ∫ 2 3 3 2 y + 9 2 — y 2 d y = = ∫ 1 2 7 2 y — 7 2 d y + ∫ 2 3 3 2 y + 9 2 — y 2 d y = = 7 4 y 2 — 7 4 y 1 2 + — y 3 3 + 3 y 2 4 + 9 2 y 2 3 = 7 4 · 2 2 — 7 4 · 2 — 7 4 · 1 2 — 7 4 · 1 + + — 3 3 3 + 3 · 3 2 4 + 9 2 · 3 — — 2 3 3 + 3 · 2 2 4 + 9 2 · 2 = = 7 4 + 23 12 = 11 3
Как видите, значения совпадают.
Ответ: S ( G ) = 11 3
Видео:Как легко составить уравнение параболы из графикаСкачать

Итоги
Для нахождения площади фигуры, которая ограничена заданными линиями нам необходимо построить линии на плоскости, найти точки их пересечения, применить формулу для нахождения площади. В данном разделе мы рассмотрели наиболее часто встречающиеся варианты задач.
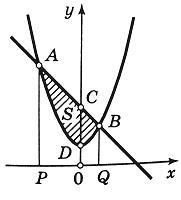
Вычислить площадь фигуры, ограниченной линиями 
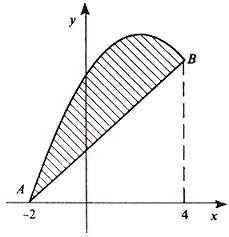
Находим точки пересечения заданных линий. Для этого решаем систему уравнений:
Для нахождения абсцисс точек пересечения заданных линий решаем уравнение:


Итак, данные линии, представляющие собой параболу и прямую, пересекаются в точках A(-2; 0), B(4; 6).
Эти линии образуют замкнутую фигуру, площадь которой вычисляем по указанной выше формуле:
По формуле Ньютона-Лейбница находим:
Найти площадь области, ограниченной эллипсом 
Из уравнения эллипса для I квадранта имеем 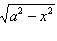

Применим подстановку x = a sin t, dx = a cos t dt. Новые пределы интегрирования t = α и t = β определяются из уравнений 0 = a sin t, a = a sin t. Можно положить α = 0 и β = π/2.
Находим одну четвертую искомой площади
Найдем точки пересечения линий y = —x 2 + x + 4, y = —x + 1, приравнивая ординаты линий: —x 2 + x + 4 = —x + 1 или x 2 — 2x — 3 = 0. Находим корни x1 = -1, x2 = 3 и соответствующие им ординаты y1 = 2, y2 = -2.
По формуле площади фигуры получаем
Решая систему уравнений
находим абсциссы точек пересечения x1 = -2 и x2 = 1.
Полагая y2 = 3 — x и y1 = x 2 + 1, на основании формулы 
В полярной системе координат площадь фигуры, ограниченной дугой кривой r = f(φ) и двумя полярными радиусами φ1 = ʅ и φ2 = ʆ, выразится интегралом
В силу симметрии кривой определяем сначала одну четвертую искомой площади
Следовательно, вся площадь равна S = a 2 .
Запишем уравнение астроиды в виде
Отсюда получаем параметрические уравнения астроиды
Ввиду симметрии кривой (*) достаточно найти одну четвертую часть длины дуги L, соответствующую изменению параметра t от 0 до π/2.
Интегрируя полученное выражение в пределах от 0 до π/2, получаем
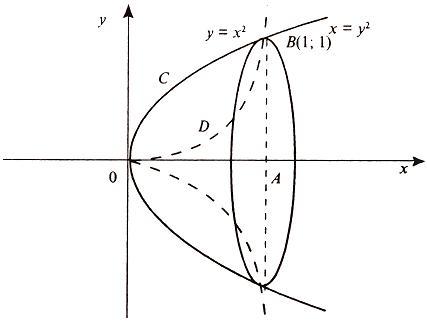
Решим систему уравнений
и получим x1 = 0, x2 = 1, y1 = 0, y2 = 1, откуда точки пересечения кривых O(0; 0), B(1; 1). Как видно на рисунке, искомый объем тела вращения равен разности двух объемов, образованных вращением вокруг оси Ox криволинейных трапеций OCBA и ODBA:
а) На отрезке [0, π] функция sin x сохраняет знак, и поэтому по формуле 
б) На отрезке [0, 2π], функция sin x меняет знак. Для корректного решения задачи, необходимо отрезок [0, 2π] разделить на два [0, π] и [π, 2π], в каждом из которых функция сохраняет знак.
По правилу знаков, на отрезке [π, 2π] площадь берется со знаком минус.
В итоге, искомая площадь равна
Определить объем тела, ограниченного поверхностью, полученной от вращения эллипса 
Учитывая, что эллипс симметричен относительно осей координат, то достаточно найти объем, образованный вращением вокруг оси Oxплощади OAB, равной одной четверти площади эллипса, и полученный результат удвоить.
Обозначим объем тела вращения через Vx; тогда на основании формулы 
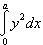

Таким образом, искомый объем равен 
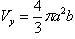
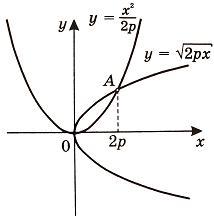
Сначала найдем координаты точек пересечения парабол, чтобы определить отрезок интегрирования. Преобразуя исходные уравнения, получаем 


Находим корни уравнений:
Учитывая то факт, что точка A пересечения парабол находится в первой четверти, то пределы интегрирования x = 0 и x = 2p.
Ключевые слова: найти площадь фигуры на рисунке, заштрихованной, закрашенной, плоской, сложной фигуры, вычислить площадь фигуры.
Предлагаем Вашему вниманию калькулятор для нахождения площади фигуры ограниченной кривыми линиями. Калькулятор в автоматическом режиме составляет интеграл, находит границы интегрирования, а также рисует саму фигуру на координатной плоскости. Как частный случай, калькулятор находит площадь криволинейной трапеции.
Видео:Площадь под параболойСкачать

Как построить параболу? Что такое парабола? Как решаются квадратные уравнения?
Урок: как построить параболу или квадратичную функцию?
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
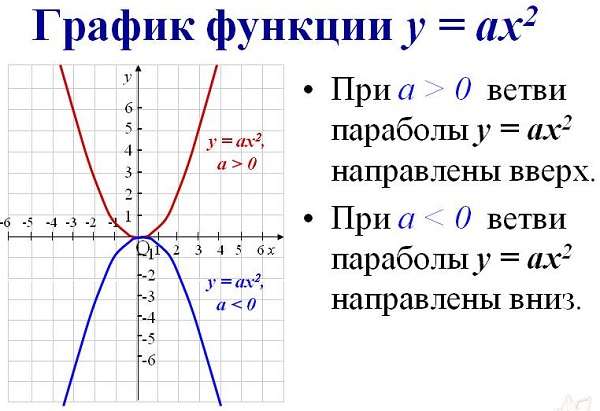
Парабола — это график функции описанный формулой ax 2 +bx+c=0.
Чтобы построить параболу нужно следовать простому алгоритму действий:
1 ) Формула параболы y=ax 2 +bx+c,
если а>0 то ветви параболы направленны вверх,
а 2 +bx+c=0;
a) Полное квадратное уравнение имеет вид ax 2 +bx+c=0 и решается по дискриминанту;
b) Неполное квадратное уравнение вида ax 2 +bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:
ax 2 +bx=0,
х(ax+b)=0,
х=0 и ax+b=0;
c)Неполное квадратное уравнение вида ax 2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);
4) Найти несколько дополнительных точек для построения функции.
ПРАКТИЧЕСКАЯ ЧАСТЬ
И так теперь на примере разберем все по действиям:
Пример №1:
y=x 2 +4x+3
c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2) 2 +4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
Найдем корни уравнения x 2 +4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b 2 -4ac=16-12=4
x=(-b±√(D))/2a
x1=(-4+2)/2=-1
x2=(-4-2)/2=-3 
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=-2
х -4 -3 -1 0
у 3 0 0 3
Подставляем вместо х в уравнение y=x 2 +4x+3 значения
y=(-4) 2 +4*(-4)+3=16-16+3=3
y=(-3) 2 +4*(-3)+3=9-12+3=0
y=(-1) 2 +4*(-1)+3=1-4+3=0
y=(0) 2 +4*(0)+3=0-0+3=3
Видно по значениям функции,что парабола симметрична относительно прямой х=-2
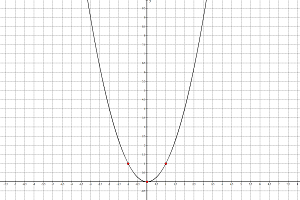
Пример №2:
y=-x 2 +4x
c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1 2 +4*2=-4+8=4 вершина находится в точке (2;4)
Найдем корни уравнения -x 2 +4x=0
Неполное квадратное уравнение вида ax 2 +bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0.
х(-x+4)=0, х=0 и x=4. 
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x 2 +4x значения
y=0 2 +4*0=0
y=-(1) 2 +4*1=-1+4=3
y=-(3) 2 +4*3=-9+13=3
y=-(4) 2 +4*4=-16+16=0
Видно по значениям функции,что парабола симметрична относительно прямой х=2
Пример №3
y=x 2 -4
c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0) 2 -4=-4 вершина находится в точке (0;-4)
Найдем корни уравнения x 2 -4=0
Неполное квадратное уравнение вида ax 2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x 2 =4
x1=2
x2=-2
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=0
х -2 -1 1 2
у 0 -3 -3 0
Подставляем вместо х в уравнение y= x 2 -4 значения
y=(-2) 2 -4=4-4=0
y=(-1) 2 -4=1-4=-3
y=1 2 -4=1-4=-3
y=2 2 -4=4-4=0
Видно по значениям функции,что парабола симметрична относительно прямой х=0
Подписывайтесь на канал на YOUTUBE, чтобы быть в курсе всех новинок и готовится с нами к экзаменам.
Видео:Определение знаков коэффициентов квадратного уравнения (параболы) по рисунку/ЗНО 2010 #25Скачать

Парабола свойства и график квадратичной функции
Что такое парабола знают, пожалуй, все. А вот как ее правильно, грамотно использовать при решении различных практических задач, разберемся ниже.
Сначала обозначим основные понятия, которые дает этому термину алгебра и геометрия. Рассмотрим все возможные виды этого графика.
Узнаем все основные характеристики этой функции. Поймем основы построения кривой (геометрия). Научимся находить вершину, другие основные величины графика данного типа.
Узнаем: как правильно строится искомая кривая по уравнению, на что надо обратить внимание. Посмотрим основное практическое применение этой уникальной величины в жизни человека.
Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Что такое парабола и как она выглядит
Алгебра: под этим термином понимается график квадратичной функции.
Геометрия: это кривая второго порядка, имеющая ряд определенных особенностей:
- Любая прямая пересекает на плоскости искомую линию в 2-х точках – так называемые, «нули» (кроме основного экстремума графика).
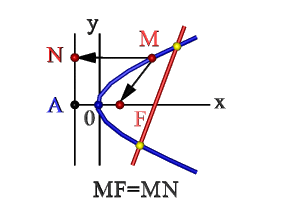
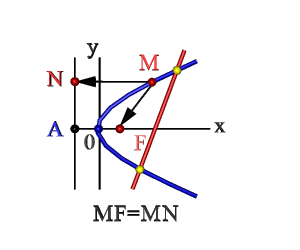
- Множество точек плоскости ХОY (М), расстояние FM которых до F = расстоянию MN до прямой Где F – фокус, AN – директриса. Эти понятия рассмотрим ниже.
Видео:КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать

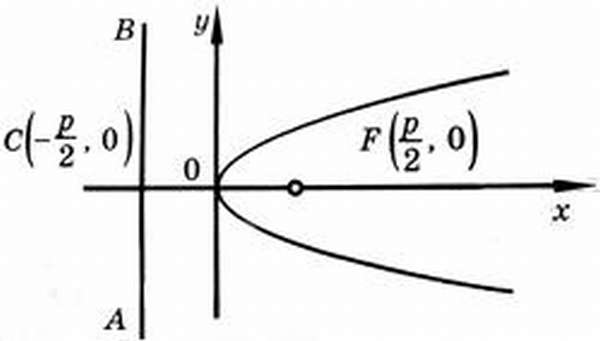
Каноническое уравнение параболы
На рисунке изображена прямоугольная система координат (XOY), экстремум, направление ветвей чертежа функции вдоль оси абсцисс.
Каноническое уравнение имеет вид:
где коэффициент p – фокальный параметр параболы (AF).
В алгебре оно запишется иначе:
y = a x2 + b x + c (узнаваемый шаблон: y = x2).
Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Свойства и график квадратичной функции
Функция обладает осью симметрии и центром (экстремум). Область определения – все значения оси абсцисс.
Область значений функции – (-∞, М) или (М, +∞) зависит от направления ветвей кривой. Параметр М тут означает величину функции в вершине линии.
Видео:§24 Каноническое уравнение параболыСкачать

Как определить, куда направлены ветви параболы
Чтобы найти направление кривой такого типа из выражения, нужно определить знак перед первым параметром алгебраического выражения. Если а ˃ 0, то они направлены вверх. Если наоборот – вниз.
Видео:Как найти вершину параболы?Скачать

Как найти вершину параболы по формуле
Нахождение экстремума является основным этапом при решении множества практических задач. Конечно, можно открыть специальные онлайн калькуляторы, но лучше это уметь делать самому.
Как же ее определить? Есть специальная формула. Когда b не равно 0, надо искать координаты этой точки.
Формулы нахождения вершины:
Пример.
Имеется функция у = 4 * x2 + 16 * x – 25. Найдём вершины этой функции.
Для такой линии:
- х = -16 / (2 * 4) = -2,
- y = 4 * 4 — 16 * 2 — 25 = 16 — 32 — 25 = -41.
Получаем координаты вершины (-2, -41).
Видео:Как думать в математике. Вершина параболы для чайников. #математика #алгебра #парабола #думатьСкачать

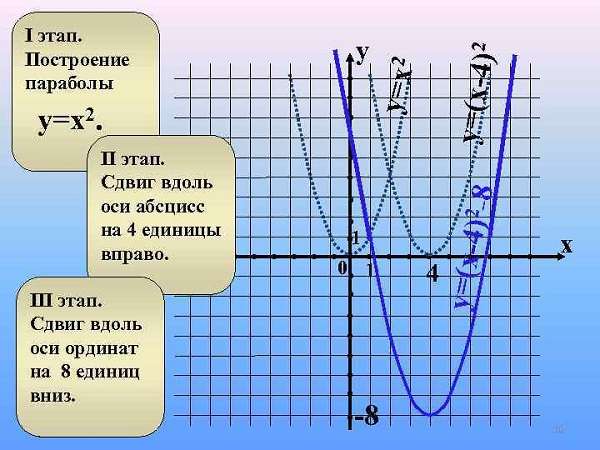
Смещение параболы
Классический случай, когда в квадратичной функции y = a x2 + b x + c, второй и третий параметры равны 0, а = 1 – вершина находится в точке (0, 0).
Движение по осям абсцисс или ординат обусловлено изменением параметров b и c соответственно. Сдвиг линии на плоскости будет осуществляться ровно на то количество единиц, чему равно значение параметра.
Пример.
Имеем: b = 2, c = 3.
Это означает, что классический вид кривой сдвинется на 2 единичных отрезка по оси абсцисс и на 3 по оси ординат.
Видео:Задача на параболу и площадь треугольникаСкачать

Как строить параболу по квадратному уравнению
Школьникам важно усвоить, как правильно начертить параболу по заданным параметрам.
Анализируя выражения и уравнения, можно увидеть следующее:
- Точка пересечения искомой линии с вектором ординат будет иметь значение, равное величине с.
- Все точки графика (по оси абсцисс) будут симметричны относительно основного экстремума функции.
Кроме того, места пересечения с ОХ можно найти, зная дискриминант (D) такой функции:
Для этого нужно приравнять выражение к нулю.
Наличие корней параболы зависит от результата:
- D ˃ 0, то х1, 2 = (-b ± D0,5) / (2 * a),
- D = 0, то х1, 2 = -b / (2 * a),
- D ˂ 0, то нет точек пересечения с вектором ОХ.
Получаем алгоритм построения параболы:
- определить направление ветвей,
- найти координаты вершины,
- найти пересечение с осью ординат,
- найти пересечение с осью абсцисс.
Пример 1.
Дана функция у = х2 5 * х + 4. Необходимо построить параболу. Действуем по алгоритму:
- а = 1, следовательно, ветви направлены вверх,
- координаты экстремума: х = (-5) / 2 = 5/2, y = (5/2)2 — 5 * (5/2) + 4 = -15/4,
- с осью ординат пересекается в значении у = 4,
- найдем дискриминант: D = 25 — 16 = 9,
- ищем корни:
- Х1 = (5 + 3) / 2 = 4, (4, 0),
- Х2 = (5 — 3) / 2 = 1, (1, 0).
По полученным точкам можно построить параболу.
Пример 2.
Для функции у = 3 * х2 2 * х 1 нужно построить параболу. Действуем по приведенному алгоритму:
- а = 3, следовательно, ветви направлены вверх,
- координаты экстремума: х = (-2) / 2 * 3 = 1/3, y = 3 * (1/3)2 — 2 * (1/3) — 1 = -4/3,
- с осью у будет пересекаться в значении у = -1,
- найдем дискриминант: D = 4 + 12 = 16. Значит корни:
- Х1 = (2 + 4) / 6 = 1, (1,0),
- Х2 = (2 — 4) / 6 = -1/3, (-1/3, 0).
По полученным точкам можно построить параболу.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Директриса, эксцентриситет, фокус параболы
Исходя из канонического уравнения, фокус F имеет координаты (p/2, 0).
Прямая АВ – директриса (своего рода хорда параболы определенной длины). Ее уравнение: х = -р/2.
Эксцентриситет (константа) = 1.
Видео:Квадратичная функция. Вершина параболы и нули функции. 8 класс.Скачать

Заключение
Мы рассмотрели тему, которую изучают школьники в средней школе. Теперь вы знаете, глядя на квадратичную функцию параболы, как найти её вершину, в какую сторону будут направлены ветви, есть ли смещение по осям, и, имея алгоритм построения, сможете начертить её график.
🌟 Видео
Парабола (часть 1). Каноническое уравнение параболы. Высшая математика.Скачать

Видеоурок "Парабола"Скачать

Парабола | Квадратный трёхчлен #2 | Ботай со мной #021 | Борис ТрушинСкачать

Как строить параболу? | TutorOnlineСкачать

А ты знаешь где находится средина параболы. #математика #алгебра #парабола #simplemath #формулаСкачать

СЕКРЕТНОЕ УРАВНЕНИЕ ПАРАБОЛЫ, которое упростит тебе жизнь #графики #парабола #уравнение #математикаСкачать