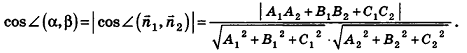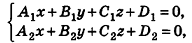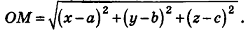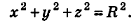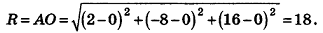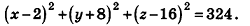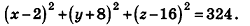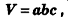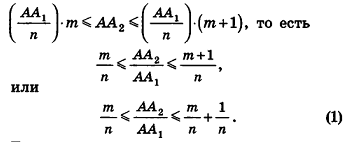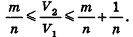Содержание:
Площади поверхностей геометрических тел:
Под площадью поверхности многогранника мы понимаем сумму площадей всех его граней. Как же определить площадь поверхности тела, не являющегося многогранником? На практике это делают так. Разбивают поверхность на такие части, которые уже мало отличаются от плоских. Тогда находят площади этих частей, как будто они являются плоскими. Сумма полученных площадей является приближенной площадью поверхности. Например, площадь крыши здания определяется как сумма площадей кусков листового металла. Еще лучше это видно на примере Земли. Приблизительно она имеет форму шара. Но площади небольших ее участков измеряют так, как будто эти участки являются плоскими. Более того, под площадью поверхности тела будем понимать предел площадей полных поверхностей описанных около него многогранников. При этом должно выполняться условие, при котором все точки поверхности этих многогранников становятся сколь угодно близкими к поверхности данного тела. Для конкретных тел вращения понятие описанного многогранника будет уточнено.
- Понятие площади поверхности
- Площадь поверхности конуса и усеченного конуса
- Связь между площадями поверхностей и объемами
- Площадь сферы
- Справочный материал
- Формулы объемов и площадей поверхностей геометрических тел
- Историческая справка
- Уравнения фигур в пространстве
- Доказательство формулы объема прямоугольного параллелепипеда
- Нахождение площади фигуры, ограниченной линиями y=f(x), x=g(y)
- Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
- Примеры вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
- Итоги
- Вычисление площадей фигур в различных системах координат
- Площадь плоской фигуры в декартовых координатах
- Площадь фигуры, ограниченной кривой, заданной параметрически
- Площадь фигуры, заданной в полярных координатах
- 📸 Видео
Видео:Как найти площадь фигуры?Скачать

Понятие площади поверхности
Рассмотрим периметры
Применим данные соотношения к обоснованию формулы для площади боковой поверхности цилиндра.
При вычислении объема цилиндра были использованы правильные вписанные в него призмы. Найдем при помощи в чем-то аналогичных рассуждений площадь боковой поверхности цилиндра.
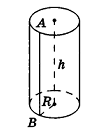
Опишем около данного цилиндра радиуса R и высоты h правильную n-угольную призму (рис. 220).
Площадь боковой поверхности призмы равна
где 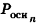
При неограниченном возрастании n получим:
так как периметры оснований призмы стремятся к длине окружности основания цилиндра, то есть к
Учитывая, что сумма площадей двух оснований призмы стремится к 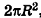
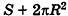
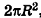
Итак, площадь боковой поверхности цилиндра вычисляется по формуле
где R — радиус цилиндра, h — его высота.
Заметим, что эта формула аналогична соответствующей формуле площади боковой поверхности прямой призмы
За площадь полной поверхности цилиндра принимается сумма площадей боковой поверхности и двух оснований:
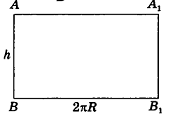
Если боковую поверхность цилиндра радиуса R и высоты h разрезать по образующей АВ и развернуть на плоскость, то в результате получим прямоугольник 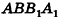
Очевидно, что сторона 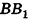
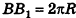
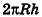
Пример:
Параллельно оси цилиндра на расстоянии d от нее проведена плоскость, отсекающая от основания дугу 
Решение:
Пусть дан цилиндр, в основаниях которого лежат равные круги с центрами 
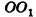
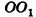
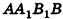
Пусть хорда АВ отсекает от окружности основания дугу 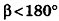
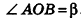
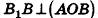
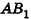
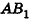
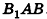
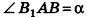
В равнобедренном треугольнике 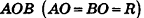
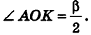
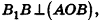
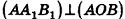
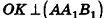
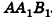
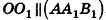
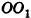
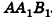
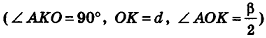
откуда 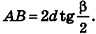
Итак,
В случае, когда
Аналогично предыдущему, и в этом случае получаем тот же результат для площади боковой поверхности.
Ответ:
Площадь поверхности конуса и усеченного конуса
Связь между цилиндрами и призмами полностью аналогична связи между конусами и пирамидами. В частности, это касается формул для площадей их боковых поверхностей.
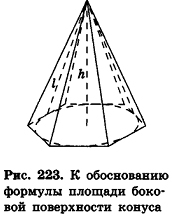
Опишем около данного конуса с радиусом основания R и образующей I правильную л-угольную пирамиду (рис. 223). Площадь ее боковой поверхности равна
где 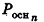
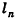
При неограниченном возрастании n получим:
так как периметры оснований пирамиды стремятся к длине окружности основания конуса, а апофемы 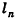
Учитывая, что площадь основания пирамиды стремится к 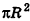
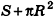
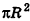
где R — радиус основания, I — образующая.
За площадь полной поверхности конуса принимается сумма площадей его основания и боковой поверхности:
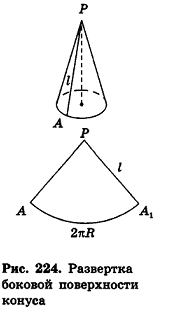
Если боковую поверхность конуса разрезать по образующей РА и развернуть на плоскость, то в результате получим круговой сектор 
Очевидно, что радиус сектора развертки равен образующей конуса I, а длина дуги 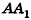
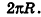
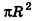
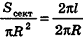
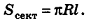
Учитывая формулу для площади боковой поверхности конуса, нетрудно найти площадь боковой поверхности усеченного конуса.
Рассмотрим усеченный конус, полученный при пересечении конуса с вершиной Р некоторой секущей плоскостью (рис. 225).
Пусть 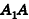
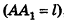
Из подобия треугольников
следует, что
Тогда получаем
Таким образом,
Итак, мы получили формулу для вычисления площади боковой поверхности усеченного конуса: 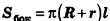
Отсюда ясно, что площадь полной поверхности усеченного конуса равна
Такой же результат можно было бы получить, если найти площадь развертки боковой поверхности усеченного конуса или использовать правильные усеченные пирамиды, описанные около него. Попробуйте дать соответствующие определения и провести необходимые рассуждения самостоятельно.
Связь между площадями поверхностей и объемами
При рассмотрении объемов и площадей поверхностей цилиндра и конуса мы видели, что существует тесная взаимосвязь между этими фигурами и призмами и пирамидами соответственно. Оказывается, что и сфера (шар), вписанная в многогранник, связана с величиной его объема.
Определение:
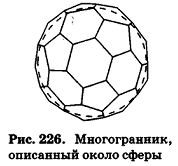
Сфера (шар) называется вписанной в выпуклый многогранник, если она касается каждой его грани.
При этом многогранник называется описанным около данной сферы (рис. 226).
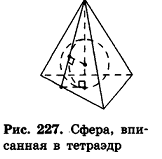
Рассмотрим, например, сферу, вписанную в тетраэдр (рис. 227).
Плоскости, содержащие грани тетраэдра, являются касательными к вписанной сфере, а точки касания лежат в гранях тетраэдра. Заметим, что по доказанному в п. 14.2 радиусы вписанной сферы, проведенные в точку касания с поверхностью многогранника, перпендикулярны плоскостям граней этого многогранника.
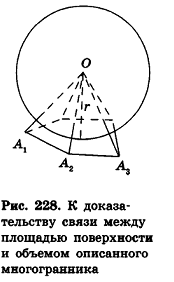
Для описанных многоугольников на плоскости было доказано, что их площадь равна произведению полупериметра на радиус вписанной окружности. Аналогичное свойство связывает объем описанного многогранника и площадь его поверхности.
Теорема (о связи площади поверхности и объема описанного многогранника)
Объем описанного многогранника вычисляется по формуле
где 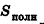
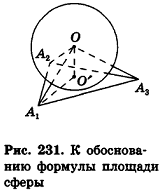
Соединим центр вписанной сферы О со всеми вершинами многогранника 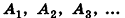
где 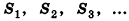
Оказывается, что в любой тетраэдр можно вписать сферу, и только одну. Но не каждый выпуклый многогранник обладает этим свойством.
Рассматривают также сферы, описанные около многогранника.
Определение:
Сфера называется описанной около многогранника, если все его вершины лежат на сфере.
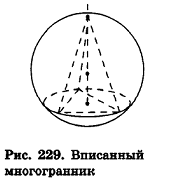
При этом многогранник называется вписанным в сферу (рис. 229).
Также считается, что соответствующий шар описан около многогранника.
Около любого тетраэдра можно описать единственную сферу, но не каждый многогранник обладает соответствующим свойством.
Площадь сферы
Применим полученную связь для объемов и площадей поверхностей описанных многогранников к выводу формулы площади сферы.
Опишем около сферы радиуса R выпуклый многогранник (рис. 230).
Пусть S’ — площадь полной поверхности данного многогранника, а любые две точки одной грани удалены друг от друга меньше чем на е. Тогда объем многогранника равен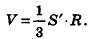
По неравенству треугольника 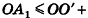
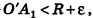
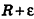
Итак, объем V данного многогранника больше объема шара радиуса R и меньше объема шара радиуса 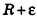
Отсюда получаем
Если неограниченно уменьшать размеры граней многогранника, то есть при е, стремящемся к нулю, левая и правая части последнего неравенства будут стремиться к 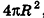
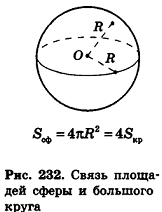
Итак, площадь сферы радиуса R вычисляется по формуле
Доказанная формула означает, что площадь сферы равна четырем площадям ее большого круга (рис. 232).
Исходя из аналогичных рассуждений, можно получить формулу для площади сферической части шарового сегмента с высотой Н:
Оказывается, что эта формула справедлива и для площади сферической поверхности шарового слоя (пояса):
где Н — высота слоя (пояса).
Справочный материал
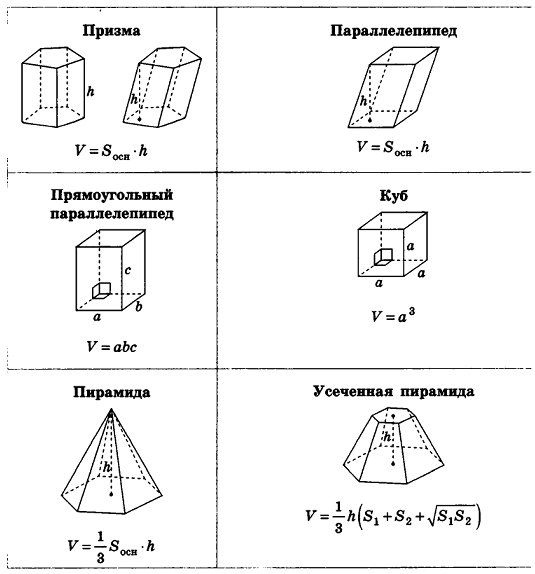
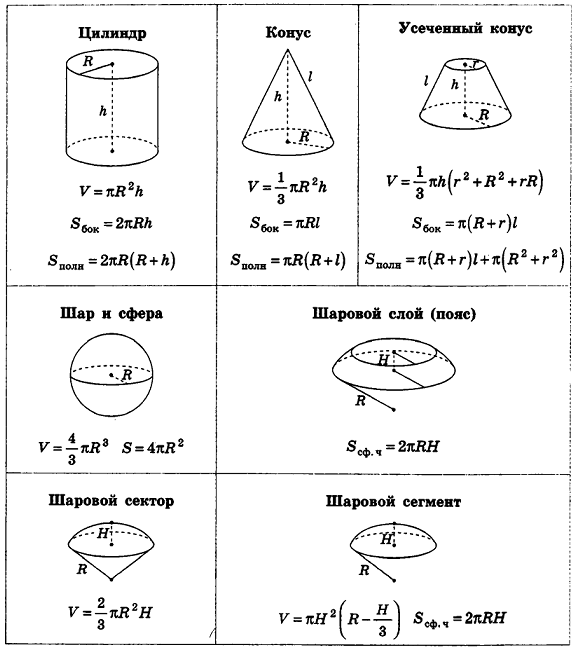
Формулы объемов и площадей поверхностей геометрических тел
Историческая справка
Многие формулы для вычисления объемов многогранников были известны уже в Древнем Египте. В так называемом Московском папирусе, созданном около 4000 лет назад, вероятно, впервые в истории вычисляется объем усеченной пирамиды. Но четкие доказательства большинства формул для объемов появились позднее, в работах древнегреческих ученых.
Так, доказательства формул для объемов конуса и пирамиды связаны с именами Демокрита из Абдеры (ок. 460-370 гг. до н. э.) и Евдокса Книдского (ок. 408-355 гг. до н. э.). На основании их идей выдающийся математик и механик Архимед (287-212 гг. до н. э.) вычислил объем шара, нашел формулы для площадей поверхностей цилиндра, конуса, сферьГг
Дальнейшее развитие методы, предложенные Архимедом, получили благодаря трудам средневекового итальянского монаха и математика Бонавентуры Кавальери (1598-1647). В своей книге «Геометрия неделимых» он сформулировал принцип сравнения объемов, при котором используются площади сечений. Его рассуждения стали основой интегральных методов вычисления объемов, разработанных Исааком Ньютоном (1642 (1643)-1727) и Готфридом Вильгельмом фон Лейбницем (1646-1716). Во многих учебниках по геометрии объем пирамиды находится с помощью * чертовой лестницы» — варианта древнегреческого метода вычерпывания, предложенного французским математиком А. М. Лежандром (1752-1833).
На II Международном конгрессе математиков, который состоялся в 1900 году в Париже, Давид Гильберт сформулировал, в частности, такую проблему: верно ли, что любые два равновеликих многогранника являются равносоставленными? Уже через год отрицательный ответ на этот вопрос был обоснован учеником Гильберта Максом Деном (1878-1952). Другое доказательство этого факта предложил в 1903 году известный геометр В. Ф. Каган, который в начале XX века вел плодотворную научную и просветительскую деятельность в Одессе. В частности, из работ Дена и Кагана следует, что доказательство формулы объема пирамиды невозможно без применения пределов.
Весомый вклад в развитие теории площадей поверхностей внесли немецкие математики XIX века. Так, в 1890 году Карл Герман Аман-дус Шварц (1843-1921) построил пример последовательности многогранных поверхностей, вписанных в боковую поверхность цилиндра («сапог Шварца»). Уменьшение их граней не приводит к приближению суммы площадей этих граней к площади боковой поверхности цилиндра. Это стало толчком к созданию выдающимся немецким математиком и физиком Германом Минков-ским (1864-1909) современной теории площадей поверхностей, в которой последние связаны с объемом слоя около данной поверхности.
Учитывая огромный вклад Архимеда в развитие математики, в частности теории объемов и площадей поверхностей, именно его изобразили на Филдсовской медали — самой почетной в мире награде для молодых математиков. В 1990 году ею был награжден Владимир Дрин-фельд (род. в 1954 г.), который учился и некоторое время работал в Харькове. Вот так юные таланты, успешно изучающие геометрию в школе, становятся в дальнейшем всемирно известными учеными.
Уравнения фигур в пространстве
Напомним, что уравнением фигуры F на плоскости называется уравнение, которому удовлетворяют координаты любой точки фигуры F и не удовлетворяют координаты ни одной точки, не принадлежащей фигуре F. Так же определяют и уравнение фигуры в пространстве; но, в отличие от плоскости, где уравнение фигуры содержит две переменные х и у, в пространстве уравнение фигуры является уравнением с тремя переменными х, у и z.
Выведем уравнение плоскости, прямой и сферы в пространстве. Для получения уравнения плоскости рассмотрим в прямоугольной системе координат плоскость а (рис. 233) и определим свойство, с помощью которого можно описать принадлежность произвольной точки данной плоскости. Пусть ненулевой вектор 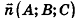
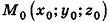
Так как 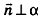
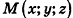
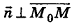
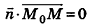
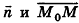
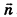
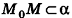
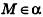
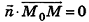
Теорема (уравнение плоскости в пространстве)
В прямоугольной системе координат уравнение плоскости имеет вид 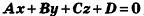
Запишем в координатной форме векторное равенство 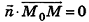
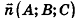
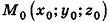
Следовательно,
После раскрытия скобок и приведения подобных членов это уравнение примет вид:
Обозначив числовое выражение в скобках через D, получим искомое уравнение, в котором числа А, В и С одновременно не равны нулю, так как 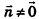
Покажем теперь, что любое уравнение вида Ах + Ву +Cz+D = 0 задает в пространстве плоскость. Действительно, пусть 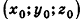
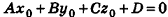
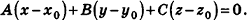
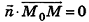
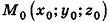
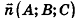
Обратим внимание на то, что в доказательстве теоремы приведен способ составления уравнения плоскости по данным координатам произвольной точки плоскости и вектора нормали.
Пример:
Напишите уравнение плоскости, которая перпендикулярна отрезку MN и проходит через его середину, если М<-1;2;3), N(5;-4;-1).
Решение:
Найдем координаты точки О — середины отрезка MN:
Значит, О (2; -1; l). Так как данная плоскость перпендикулярна отрезку MN, то вектор 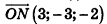
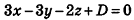
И наконец, так как данная плоскость проходит через точку О(2;-l;l), то, подставив координаты этой точки в уравнение, получим:
Таким образом, уравнение 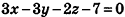
Ответ:
Заметим, что правильным ответом в данной задаче является также любое уравнение, полученное из приведенного умножением обеих частей на число, отличное от нуля.
Значения коэффициентов А, В, С и D в уравнении плоскости определяют особенности расположения плоскости в системе координат. В частности:
- если
, уравнение плоскости примет вид Ax+By+Cz = 0; очевидно, что такая плоскость проходит через начало координат (рис. 234, а);
- если один из коэффициентов А, В и С равен нулю, a
, плоскость параллельна одной из координатных осей: например, при условии А = 0 вектор нормали
перпендикулярен оси Ох, а плоскость By + Cz + D = Q параллельна оси Ох (рис. 234, б)
- если два из коэффициентов А, В и С равны нулю, а
, плоскость параллельна одной из координатных плоскостей: например, при условиях А = 0 и В-О вектор нормали
перпендикулярен плоскости Оху, а плоскость Cz+D = 0 параллельна плоскости Оху (рис. 234, в);
- если два из коэффициентов А, В и С равны нулю и D = 0, плоскость совпадает с одной из координатных плоскостей: например, при условиях
и В = С = D = 0 уравнение плоскости имеет вид Ах = О, или х= 0, то есть является уравнением плоскости Оуz (рис. 234, г).
Предлагаем вам самостоятельно составить полную таблицу частных случаев расположения плоскости Ax + By+Cz+D = 0 в прямоугольной системе координат в зависимости от значений коэффициентов А, В, С и D.
Пример: (о расстоянии от точки до плоскости)
Расстояние от точки 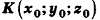
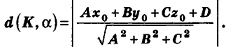
Решение:
Если 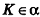
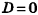
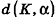
Если 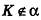
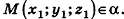
Тогда 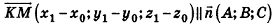
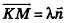
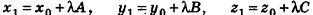
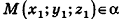
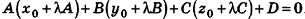
Таким образом,
Рассмотрим теперь возможность описания прямой в пространстве с помощью уравнений.
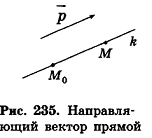
Пусть в пространстве дана прямая k (рис. 235). Выберем ненулевой вектор 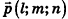
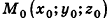
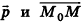
Представим это векторное равенство в координатной форме. Если ни одна из координат направляющего вектора не равна нулю, из данного равенства можно выразить t и приравнять полученные результаты:
Эти равенства называют каноническими уравнениями прямой в пространстве.
Пример:
Напишите уравнение прямой, проходящей через точки А(1;-3;2) и В(-l;0;l).
Решение:
Так как точки А и В принадлежат данной прямой, то 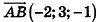
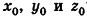
Ответ:
Заметим, что ответ в этой задаче может иметь и другой вид: так, в числителях дробей можно использовать координаты точки В, а как направляющий вектор рассматривать любой ненулевой вектор, коллинеарный 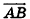
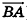
Вообще, если прямая в пространстве задана двумя точками 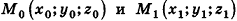
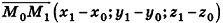
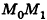
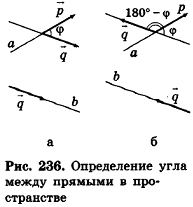
С помощью уравнений удобно исследовать взаимное расположение прямых и плоскостей в пространстве. Рассмотрим прямые 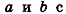
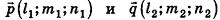
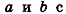
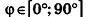
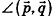
Так как cos(l80°-ф) = -coscp, имеем 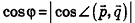
Отсюда, в частности, следует необходимое и достаточное условие перпендикулярности прямых 
Кроме того, прямые 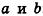
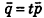
Проанализируем теперь отдельные случаи взаимного расположения двух плоскостей в пространстве. Очевидно, что если 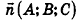
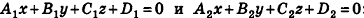
- совпадают, если существует число t такое, что
, или, если числа
ненулевые
- параллельны, если существует число t такое, что
, или, если координаты
ненулевые,
(на практике это означает, что уравнения данных плоскостей можно привести к виду Ax+By+Cz+D1= 0 и Ax+By+Cz+D2=0, где
).
В остальных случаях данные плоскости 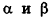
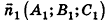
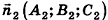
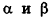
В частности, необходимое и достаточное условие перпендикулярности плоскостей 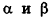
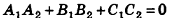
Заметим также, что прямая в пространстве может быть описана как линия пересечения двух плоскостей, то есть системой уравнений
где векторы 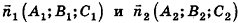
Пример:
Напишите уравнение плоскости, которая проходит через точку М(4;2;3) и параллельна плоскости x-y + 2z-S = 0.
Решение:
Так как искомая плоскость параллельна данной, то вектор нормали к данной плоскости 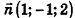
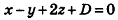
Аналогично уравнению окружности на плоскости, в пространственной декартовой системе координат можно вывести уравнение сферы с заданным центром и радиусом.
Теорема (уравнение сферы)
В прямоугольной системе координат уравнение сферы радиуса R с центром в точке 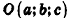
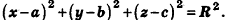
Пусть 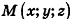
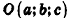
Так как OM=R, то есть ОМ 2 = R 2 , то координаты точки М удовлетворяют уравнению 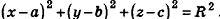
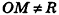
Сфера радиуса R с центром в начале координат задается уравнением вида
Заметим, что фигуры в пространстве, как и на плоскости, могут задаваться не только уравнениями, но и неравенствами. Например, шар радиуса R с центром в точке 
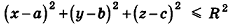
Пример:
Напишите уравнение сферы с центром А (2;-8; 16), которая проходит через начало координат.
Решение:
Так как данная сфера проходит через точку 0(0;0;0), то отрезок АО является ее радиусом. Значит,
Таким образом, искомое уравнение имеет вид:
Ответ:
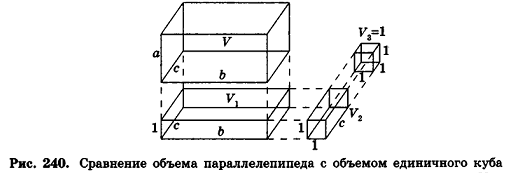
Доказательство формулы объема прямоугольного параллелепипеда
Теорема (формула объема прямоугольного параллелепипеда)
Объем прямоугольного параллелепипеда равен произведению трех его измерений:
где 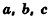
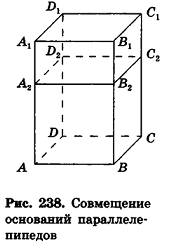
Докажем сначала, что объемы двух прямоугольных параллелепипедов с равными основаниями относятся как длины их высот.
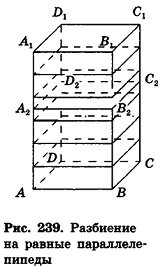
Пусть 
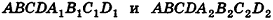
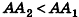
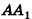
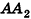
проведем через точки деления параллельные основанию ABCD (рис. 239). Они разобьют параллелепипед 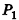
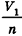
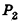
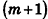
Таким образом, 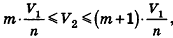
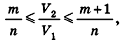
Сравнивая выражения (1) и (2), видим, что оба отношения 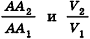
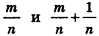
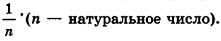
Допустим, что это не так, то есть 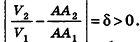
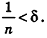
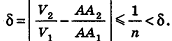
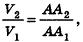
Рассмотрим теперь прямоугольные параллелепипеды с измерениями 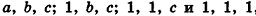
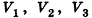
По аксиоме объема V3 =1. По доказанному 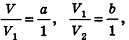
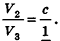
* Выберем 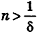
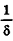
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Вычисление площадей плоских фигур
- Преобразование фигур в геометрии
- Многоугольник
- Площадь многоугольника
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Четырехугольник
- Площади фигур в геометрии
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать

Нахождение площади фигуры, ограниченной линиями y=f(x), x=g(y)
В предыдущем разделе, посвященном разбору геометрического смысла определенного интеграла, мы получили ряд формул для вычисления площади криволинейной трапеции:
S ( G ) = ∫ a b f ( x ) d x для непрерывной и неотрицательной функции y = f ( x ) на отрезке [ a ; b ] ,
S ( G ) = — ∫ a b f ( x ) d x для непрерывной и неположительной функции y = f ( x ) на отрезке [ a ; b ] .
Эти формулы применимы для решения относительно простых задач. На деле же нам чаще придется работать с более сложными фигурами. В связи с этим, данный раздел мы посвятим разбору алгоритмов вычисления площади фигур, которые ограничены функциями в явном виде, т.е. как y = f ( x ) или x = g ( y ) .
Видео:Площадь фигурыСкачать

Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
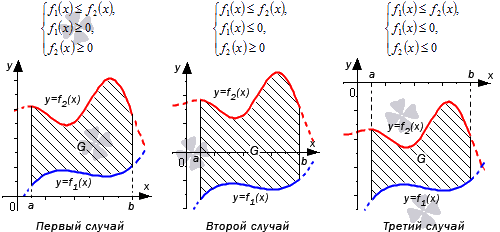
Пусть функции y = f 1 ( x ) и y = f 2 ( x ) определены и непрерывны на отрезке [ a ; b ] , причем f 1 ( x ) ≤ f 2 ( x ) для любого значения x из [ a ; b ] . Тогда формула для вычисления площади фигуры G , ограниченной линиями x = a , x = b , y = f 1 ( x ) и y = f 2 ( x ) будет иметь вид S ( G ) = ∫ a b f 2 ( x ) — f 1 ( x ) d x .
Похожая формула будет применима для площади фигуры, ограниченной линиями y = c , y = d , x = g 1 ( y ) и x = g 2 ( y ) : S ( G ) = ∫ c d ( g 2 ( y ) — g 1 ( y ) d y .
Разберем три случая, для которых формула будет справедлива.
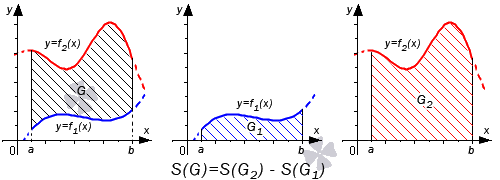
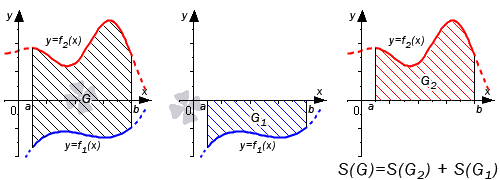
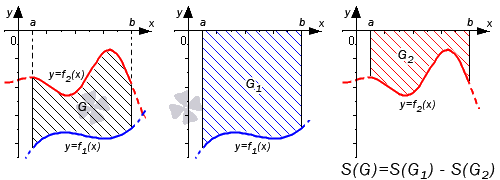
В первом случае, учитывая свойство аддитивности площади, сумма площадей исходной фигуры G и криволинейной трапеции G 1 равна площади фигуры G 2 . Это значит, что
Поэтому, S ( G ) = S ( G 2 ) — S ( G 1 ) = ∫ a b f 2 ( x ) d x — ∫ a b f 1 ( x ) d x = ∫ a b ( f 2 ( x ) — f 1 ( x ) ) d x .
Выполнить последний переход мы можем с использованием третьего свойства определенного интеграла.
Во втором случае справедливо равенство: S ( G ) = S ( G 2 ) + S ( G 1 ) = ∫ a b f 2 ( x ) d x + — ∫ a b f 1 ( x ) d x = ∫ a b ( f 2 ( x ) — f 1 ( x ) ) d x
Графическая иллюстрация будет иметь вид:
Если обе функции неположительные, получаем: S ( G ) = S ( G 2 ) — S ( G 1 ) = — ∫ a b f 2 ( x ) d x — — ∫ a b f 1 ( x ) d x = ∫ a b ( f 2 ( x ) — f 1 ( x ) ) d x . Графическая иллюстрация будет иметь вид:
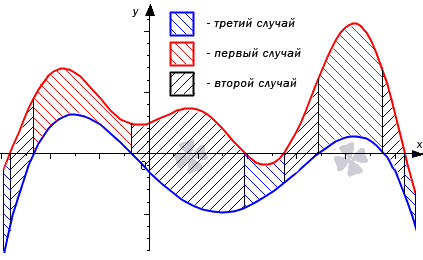
Перейдем к рассмотрению общего случая, когда y = f 1 ( x ) и y = f 2 ( x ) пересекают ось O x .
Точки пересечения мы обозначим как x i , i = 1 , 2 , . . . , n — 1 . Эти точки разбивают отрезок [ a ; b ] на n частей x i — 1 ; x i , i = 1 , 2 , . . . , n , где α = x 0 x 1 x 2 . . . x n — 1 x n = b . Фигуру G можно представить объединением фигур G i , i = 1 , 2 , . . . , n . Очевидно, что на своем интервале G i попадает под один из трех рассмотренных ранее случаев, поэтому их площади находятся как S ( G i ) = ∫ x i — 1 x i ( f 2 ( x ) — f 1 ( x ) ) d x , i = 1 , 2 , . . . , n
S ( G ) = ∑ i = 1 n S ( G i ) = ∑ i = 1 n ∫ x i x i f 2 ( x ) — f 1 ( x ) ) d x = = ∫ x 0 x n ( f 2 ( x ) — f ( x ) ) d x = ∫ a b f 2 ( x ) — f 1 ( x ) d x
Последний переход мы можем осуществить с использованием пятого свойства определенного интеграла.
Проиллюстрируем на графике общий случай.
Формулу S ( G ) = ∫ a b f 2 ( x ) — f 1 ( x ) d x можно считать доказанной.
А теперь перейдем к разбору примеров вычисления площади фигур, которые ограничены линиями y = f ( x ) и x = g ( y ) .
Видео:Как найти площадь фигуры, заданной на координатной плоскости двойным неравенствомСкачать

Примеры вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
Рассмотрение любого из примеров мы будем начинать с построения графика. Изображение позволит нам представлять сложные фигуры как объединения более простых фигур. Если построение графиков и фигур на них вызывает у вас затруднения, можете изучить раздел об основных элементарных функциях, геометрическом преобразовании графиков функций, а также построению графиков во время исследования функции.
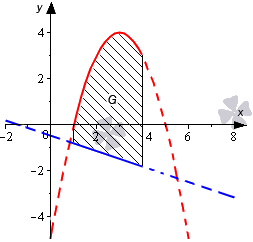
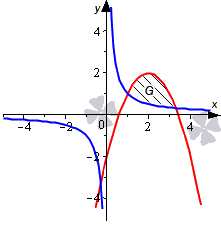
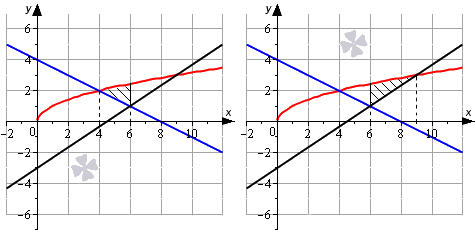
Необходимо определить площадь фигуры, которая ограничена параболой y = — x 2 + 6 x — 5 и прямыми линиями y = — 1 3 x — 1 2 , x = 1 , x = 4 .
Решение
Изобразим линии на графике в декартовой системе координат.
На отрезке [ 1 ; 4 ] график параболы y = — x 2 + 6 x — 5 расположен выше прямой y = — 1 3 x — 1 2 . В связи с этим, для получения ответа используем формулу, полученную ранее, а также способ вычисления определенного интеграла по формуле Ньютона-Лейбница:
S ( G ) = ∫ 1 4 — x 2 + 6 x — 5 — — 1 3 x — 1 2 d x = = ∫ 1 4 — x 2 + 19 3 x — 9 2 d x = — 1 3 x 3 + 19 6 x 2 — 9 2 x 1 4 = = — 1 3 · 4 3 + 19 6 · 4 2 — 9 2 · 4 — — 1 3 · 1 3 + 19 6 · 1 2 — 9 2 · 1 = = — 64 3 + 152 3 — 18 + 1 3 — 19 6 + 9 2 = 13
Ответ: S ( G ) = 13
Рассмотрим более сложный пример.
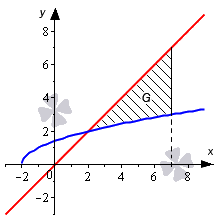
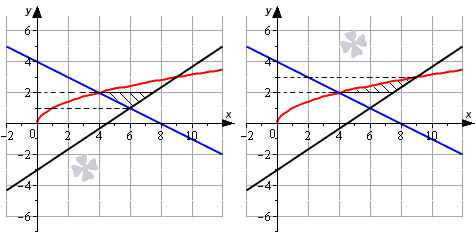
Необходимо вычислить площадь фигуры, которая ограничена линиями y = x + 2 , y = x , x = 7 .
Решение
В данном случае мы имеем только одну прямую линию, расположенную параллельно оси абсцисс. Это x = 7 . Это требует от нас найти второй предел интегрирования самостоятельно.
Построим график и нанесем на него линии, данные в условии задачи.
Имея график перед глазами, мы легко можем определить, что нижним пределом интегрирования будет абсцисса точки пересечения графика прямой y = x и полу параболы y = x + 2 . Для нахождения абсциссы используем равенства:
y = x + 2 О Д З : x ≥ — 2 x 2 = x + 2 2 x 2 — x — 2 = 0 D = ( — 1 ) 2 — 4 · 1 · ( — 2 ) = 9 x 1 = 1 + 9 2 = 2 ∈ О Д З x 2 = 1 — 9 2 = — 1 ∉ О Д З
Получается, что абсциссой точки пересечения является x = 2 .
Обращаем ваше внимание на тот факт, что в общем примере на чертеже линии y = x + 2 , y = x пересекаются в точке ( 2 ; 2 ) , поэтому такие подробные вычисления могут показаться излишними. Мы привели здесь такое подробное решение только потому, что в более сложных случаях решение может быть не таким очевидным. Это значит, что координаты пересечения линий лучше всегда вычислять аналитически.
На интервале [ 2 ; 7 ] график функции y = x расположен выше графика функции y = x + 2 . Применим формулу для вычисления площади:
S ( G ) = ∫ 2 7 ( x — x + 2 ) d x = x 2 2 — 2 3 · ( x + 2 ) 3 2 2 7 = = 7 2 2 — 2 3 · ( 7 + 2 ) 3 2 — 2 2 2 — 2 3 · 2 + 2 3 2 = = 49 2 — 18 — 2 + 16 3 = 59 6
Ответ: S ( G ) = 59 6
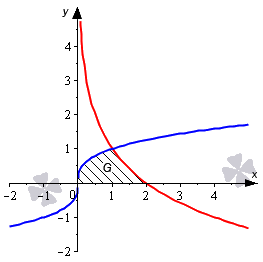
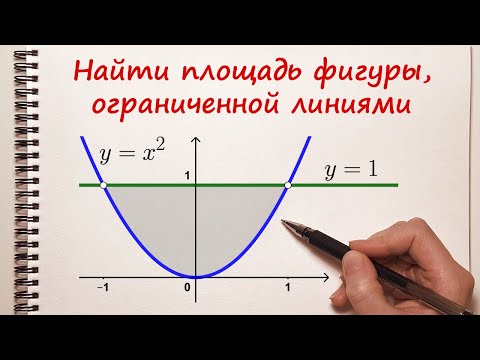
Необходимо вычислить площадь фигуры, которая ограничена графиками функций y = 1 x и y = — x 2 + 4 x — 2 .
Решение
Нанесем линии на график.
Определимся с пределами интегрирования. Для этого определим координаты точек пересечения линий, приравняв выражения 1 x и — x 2 + 4 x — 2 . При условии, что x не равно нулю, равенство 1 x = — x 2 + 4 x — 2 становится эквивалентным уравнению третьей степени — x 3 + 4 x 2 — 2 x — 1 = 0 с целыми коэффициентами. Освежить в памяти алгоритм по решению таких уравнений мы можете, обратившись к разделу «Решение кубических уравнений».
Корнем этого уравнения является х = 1 : — 1 3 + 4 · 1 2 — 2 · 1 — 1 = 0 .
Разделив выражение — x 3 + 4 x 2 — 2 x — 1 на двучлен x — 1 , получаем: — x 3 + 4 x 2 — 2 x — 1 ⇔ — ( x — 1 ) ( x 2 — 3 x — 1 ) = 0
Оставшиеся корни мы можем найти из уравнения x 2 — 3 x — 1 = 0 :
x 2 — 3 x — 1 = 0 D = ( — 3 ) 2 — 4 · 1 · ( — 1 ) = 13 x 1 = 3 + 13 2 ≈ 3 . 3 ; x 2 = 3 — 13 2 ≈ — 0 . 3
Мы нашли интервал x ∈ 1 ; 3 + 13 2 , на котором фигура G заключена выше синей и ниже красной линии. Это помогает нам определить площадь фигуры:
S ( G ) = ∫ 1 3 + 13 2 — x 2 + 4 x — 2 — 1 x d x = — x 3 3 + 2 x 2 — 2 x — ln x 1 3 + 13 2 = = — 3 + 13 2 3 3 + 2 · 3 + 13 2 2 — 2 · 3 + 13 2 — ln 3 + 13 2 — — — 1 3 3 + 2 · 1 2 — 2 · 1 — ln 1 = 7 + 13 3 — ln 3 + 13 2
Ответ: S ( G ) = 7 + 13 3 — ln 3 + 13 2
Необходимо вычислить площадь фигуры, которая ограничена кривыми y = x 3 , y = — log 2 x + 1 и осью абсцисс.
Решение
Нанесем все линии на график. Мы можем получить график функции y = — log 2 x + 1 из графика y = log 2 x , если расположим его симметрично относительно оси абсцисс и поднимем на одну единицу вверх. Уравнение оси абсцисс у = 0 .
Обозначим точки пересечения линий.
Как видно из рисунка, графики функций y = x 3 и y = 0 пересекаются в точке ( 0 ; 0 ) . Так получается потому, что х = 0 является единственным действительным корнем уравнения x 3 = 0 .
x = 2 является единственным корнем уравнения — log 2 x + 1 = 0 , поэтому графики функций y = — log 2 x + 1 и y = 0 пересекаются в точке ( 2 ; 0 ) .
x = 1 является единственным корнем уравнения x 3 = — log 2 x + 1 . В связи с этим графики функций y = x 3 и y = — log 2 x + 1 пересекаются в точке ( 1 ; 1 ) . Последнее утверждение может быть неочевидным, но уравнение x 3 = — log 2 x + 1 не может иметь более одного корня, так как функция y = x 3 является строго возрастающей, а функция y = — log 2 x + 1 строго убывающей.
Дальнейшее решение предполагает несколько вариантов.
Вариант №1
Фигуру G мы можем представить как сумму двух криволинейных трапеций, расположенных выше оси абсцисс, первая из которых располагается ниже средней линии на отрезке x ∈ 0 ; 1 , а вторая ниже красной линии на отрезке x ∈ 1 ; 2 . Это значит, что площадь будет равна S ( G ) = ∫ 0 1 x 3 d x + ∫ 1 2 ( — log 2 x + 1 ) d x .
Вариант №2
Фигуру G можно представить как разность двух фигур, первая из которых расположена выше оси абсцисс и ниже синей линии на отрезке x ∈ 0 ; 2 , а вторая между красной и синей линиями на отрезке x ∈ 1 ; 2 . Это позволяет нам найти площадь следующим образом:
S ( G ) = ∫ 0 2 x 3 d x — ∫ 1 2 x 3 — ( — log 2 x + 1 ) d x
В этом случае для нахождения площади придется использовать формулу вида S ( G ) = ∫ c d ( g 2 ( y ) — g 1 ( y ) ) d y . Фактически, линии, которые ограничивают фигуру, можно представить в виде функций от аргумента y .
Разрешим уравнения y = x 3 и — log 2 x + 1 относительно x :
y = x 3 ⇒ x = y 3 y = — log 2 x + 1 ⇒ log 2 x = 1 — y ⇒ x = 2 1 — y
Получим искомую площадь:
S ( G ) = ∫ 0 1 ( 2 1 — y — y 3 ) d y = — 2 1 — y ln 2 — y 4 4 0 1 = = — 2 1 — 1 ln 2 — 1 4 4 — — 2 1 — 0 ln 2 — 0 4 4 = — 1 ln 2 — 1 4 + 2 ln 2 = 1 ln 2 — 1 4
Ответ: S ( G ) = 1 ln 2 — 1 4
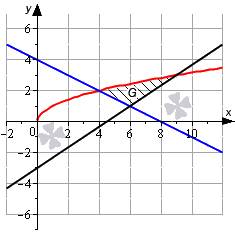
Необходимо вычислить площадь фигуры, которая ограничена линиями y = x , y = 2 3 x — 3 , y = — 1 2 x + 4 .
Решение
Красной линией нанесем на график линию, заданную функцией y = x . Синим цветом нанесем линию y = — 1 2 x + 4 , черным цветом обозначим линию y = 2 3 x — 3 .
Отметим точки пересечения.
Найдем точки пересечения графиков функций y = x и y = — 1 2 x + 4 :
x = — 1 2 x + 4 О Д З : x ≥ 0 x = — 1 2 x + 4 2 ⇒ x = 1 4 x 2 — 4 x + 16 ⇔ x 2 — 20 x + 64 = 0 D = ( — 20 ) 2 — 4 · 1 · 64 = 144 x 1 = 20 + 144 2 = 16 ; x 2 = 20 — 144 2 = 4 П р о в е р к а : x 1 = 16 = 4 , — 1 2 x 1 + 4 = — 1 2 · 16 + 4 = — 4 ⇒ x 1 = 16 н е я в л я е т с я р е ш е н и е м у р а в н е н и я x 2 = 4 = 2 , — 1 2 x 2 + 4 = — 1 2 · 4 + 4 = 2 ⇒ x 2 = 4 я в л я е т с я р е ш е н и е м у р а в н и н и я ⇒ ( 4 ; 2 ) т о ч к а п е р е с е ч е н и я y = x и y = — 1 2 x + 4
Найдем точку пересечения графиков функций y = x и y = 2 3 x — 3 :
x = 2 3 x — 3 О Д З : x ≥ 0 x = 2 3 x — 3 2 ⇔ x = 4 9 x 2 — 4 x + 9 ⇔ 4 x 2 — 45 x + 81 = 0 D = ( — 45 ) 2 — 4 · 4 · 81 = 729 x 1 = 45 + 729 8 = 9 , x 2 45 — 729 8 = 9 4 П р о в е р к а : x 1 = 9 = 3 , 2 3 x 1 — 3 = 2 3 · 9 — 3 = 3 ⇒ x 1 = 9 я в л я е т с я р е ш е н и е м у р а в н е н и я ⇒ ( 9 ; 3 ) т о ч к а п е р е с е ч а н и я y = x и y = 2 3 x — 3 x 2 = 9 4 = 3 2 , 2 3 x 1 — 3 = 2 3 · 9 4 — 3 = — 3 2 ⇒ x 2 = 9 4 н е я в л я е т с я р е ш е н и е м у р а в н е н и я
Найдем точку пересечения линий y = — 1 2 x + 4 и y = 2 3 x — 3 :
— 1 2 x + 4 = 2 3 x — 3 ⇔ — 3 x + 24 = 4 x — 18 ⇔ 7 x = 42 ⇔ x = 6 — 1 2 · 6 + 4 = 2 3 · 6 — 3 = 1 ⇒ ( 6 ; 1 ) т о ч к а п е р е с е ч е н и я y = — 1 2 x + 4 и y = 2 3 x — 3
Дальше мы можем продолжить вычисления двумя способами.
Способ №1
Представим площадь искомой фигуры как сумму площадей отдельных фигур.
Тогда площадь фигуры равна:
S ( G ) = ∫ 4 6 x — — 1 2 x + 4 d x + ∫ 6 9 x — 2 3 x — 3 d x = = 2 3 x 3 2 + x 2 4 — 4 x 4 6 + 2 3 x 3 2 — x 2 3 + 3 x 6 9 = = 2 3 · 6 3 2 + 6 2 4 — 4 · 6 — 2 3 · 4 3 2 + 4 2 4 — 4 · 4 + + 2 3 · 9 3 2 — 9 2 3 + 3 · 9 — 2 3 · 6 3 2 — 6 2 3 + 3 · 6 = = — 25 3 + 4 6 + — 4 6 + 12 = 11 3
Способ №2
Площадь исходной фигуры можно представить как сумму двух других фигур.
Тогда решим уравнение линии относительно x , а только после этого применим формулу вычисления площади фигуры.
y = x ⇒ x = y 2 к р а с н а я л и н и я y = 2 3 x — 3 ⇒ x = 3 2 y + 9 2 ч е р н а я л и н и я y = — 1 2 x + 4 ⇒ x = — 2 y + 8 с и н я я л и н и я
Таким образом, площадь равна:
S ( G ) = ∫ 1 2 3 2 y + 9 2 — — 2 y + 8 d y + ∫ 2 3 3 2 y + 9 2 — y 2 d y = = ∫ 1 2 7 2 y — 7 2 d y + ∫ 2 3 3 2 y + 9 2 — y 2 d y = = 7 4 y 2 — 7 4 y 1 2 + — y 3 3 + 3 y 2 4 + 9 2 y 2 3 = 7 4 · 2 2 — 7 4 · 2 — 7 4 · 1 2 — 7 4 · 1 + + — 3 3 3 + 3 · 3 2 4 + 9 2 · 3 — — 2 3 3 + 3 · 2 2 4 + 9 2 · 2 = = 7 4 + 23 12 = 11 3
Как видите, значения совпадают.
Ответ: S ( G ) = 11 3
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Итоги
Для нахождения площади фигуры, которая ограничена заданными линиями нам необходимо построить линии на плоскости, найти точки их пересечения, применить формулу для нахождения площади. В данном разделе мы рассмотрели наиболее часто встречающиеся варианты задач.
Видео:Найти площадь фигуры, ограниченной линиями. Пример 1.Скачать
Вычисление площадей фигур в различных системах координат
Видео:Площади фигур. Сохраняй и запоминай!#shortsСкачать

Площадь плоской фигуры в декартовых координатах
Напомним, что мы назвали криволинейной трапецией фигуру, ограниченную осью абсцисс, прямыми и и графиком функции . В этом пункте выведем формулу для вычисления площади криволинейной трапеции.
Теорема 3. Если функция неотрицательна на отрезке и непрерывна на нем, то соответствующая ей криволинейная трапеция квадрируема, причем ее площадь выражается формулой
Доказательство. Криволинейная трапеция ограничена тремя отрезками и графиком непрерывной функции . Как было показано в пункте 2 такая фигура квадрируема. Чтобы вычислить площадь этой трапеции, построим для нее внешние и внутренние ступенчатые фигуры (см. рис. 26).
Тогда, с одной стороны, имеем:
где — площадь внутренней ступенчатой фигуры, —площадь внешней ступенчатой фигуры, и . С другой стороны, по определению интеграла можно записать:
Таким образом, числа и разделяют одни и те же числовые множества: . Но, как было показано при изучении определенного интеграла, эти множества разделяются лишь одним числом, и потому . Теорема доказана.
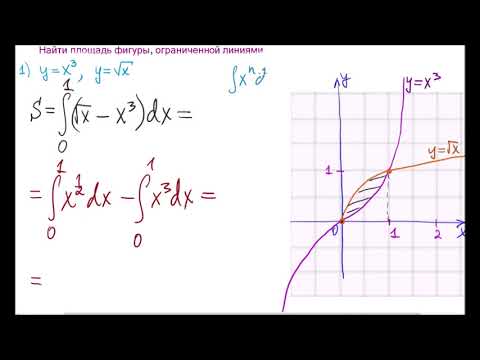
Аналогично доказывается, что если фигура ограничена снизу графиком функции , сверху графиком функции , а слева и справа прямыми (рис. 30), то ее площадь выражается формулой
Наглядный смысл формулы (4) состоит в том, что криволинейную трапецию можно рассматривать как объединение «бесконечно тонких полосок» с основаниями и высотами .
Пусть теперь функция непрерывна на отрезке и принимает на нем только неположительные значения. Выразим с помощью определенного интеграла площадь соответствующей криволинейной трапеции .
Рассмотрим фигуру , симметричную фигуре относительно оси . Эта фигура (рис. 31) представляет собой криволинейную трапецию, ограниченную сверху графиком непрерывной на отрезке функции , которая на принимает только неотрицательные значения. По доказанному выше
Как мы видим, в рассматриваемом случае интеграл дает значение площади криволинейной трапеции с точностью до знака. Если же функция меняет знак на отрезке в конечном числе точек, то значение интеграла дает алгебраическую сумму площадей соответствующих криволинейных трапеций, ограниченных частями графика функции , отрезками оси и, быть может, отрезками, параллельными оси (рис. 32).
Пример 1. Найти площадь фигуры, ограниченной кривой , осью абсцисс и прямыми (рис. 33).
Решение. Имеем: (кв. ед.).
Пример 2. Вычислить площадь фигуры, ограниченной дугой параболы и отрезком прямой (рис. 34).
Решение. Из рисунка видно, что трапеция, площадь которой нужно найти, расположена симметрично относительно оси абсцисс и, следовательно, искомая площадь равна
Пример 3. Найти площадь фигуры, ограниченной графиками функций (рис. 35).
Решение. Искомая площадь равна разности площадей криволинейного треугольника и прямоугольного треугольника
Пример 4. Вычислить площадь фигуры, ограниченной петлей кривой .
Решение. Из уравнения кривой видно, что она расположена симметрично относительно оси . Следовательно, можно сначала вычислить половину искомой площади (рис. 36). Рекомендуем читателю подробно исследовать и построить данную кривую.
Записав уравнение кривой в виде , найдем точки пересечения ее с осью , положив . Учитывая сказанное, найдем площадь половины петли:
Воспользовавшись формулой из таблицы при , получим:
Значит, окончательно имеем:
Видео:Площади фигур на плоскости. Учим формулы.Скачать

Площадь фигуры, ограниченной кривой, заданной параметрически
Пусть кривая задана в параметрической форме
где функция монотонна на отрезке , причем , и имеет на этом отрезке непрерывную производную. Так как , то по формуле замены переменной под знаком определенного интеграла получаем:
Итак, площадь фигуры, ограниченной кривой, заданной параметрически, вычисляется по формуле:
Пример 5. Вычислить площадь эллипса, заданного параметрически
Решение. Выберем ту часть эллипса (рис. 37), которая расположена в первом квадранте. Точке соответствует значение , а точке — значение . Поэтому
Видео:Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Площадь фигуры, заданной в полярных координатах
Вычислить площадь сектора, ограниченного лучами и , выходящими из точки , и непрерывной кривой (рис. 38). Выберем полярную систему координат, полюсом которой является точка . Пусть — полярное уравнение кривой , а и — углы между полярной осью и лучами и соответственно. При этом пусть функция непрерывна на .
Разобьем данный сектор на частей лучами
и рассмотрим k-й частичный сектор (рис. 39). Пусть — наименьшее значение функции в , a — наибольшее значение функции в этом отрезке.
Построим два круговых сектора с радиусами и . Обозначим через величину угла рассматриваемого частичного сектора. Тогда площадь частичного криволинейного сектора будет заключена между площадями вписанного и описанного частичных круговых секторов
Построим аналогичным образом внутренние и внешние круговые секторы для всех частичных криволинейных секторов. Объединяя их, получим внутреннюю и внешнюю фигуры.
Площадь внутренней фигуры, состоящей из круговых секторов, равна , а площадь внешней фигуры равна — . Эти выражения являются нижней и верхней суммами Дарбу и для интеграла . Так как функция непрерывна, то непрерывна, а потому и интегрируема функция . Поэтому для любого найдется такое разбиение отрезка , что . Из теоремы 2 пункта 2 следует, что заданный криволинейный сектор квадрируем. При этом для его площади выполняются неравенства
В то же время по определению определенного интеграла
В силу единственности разделяющего числа из неравенств (6) и (7) следует, что
Пример 6. Вычислить площадь, ограниченную одним лепестком розы (рис. 40).
📸 Видео
Криволинейная трапеция и ее площадь. 11 класс.Скачать

Найти площадь фигуры, заданной неравенством - 3Скачать

Определённый интеграл. ПлощадьСкачать
Вычислите площадь фигуры, ограниченной линиямиСкачать

Интегралы №12 Вычисление площадейСкачать

Самый простой способ нахождения площадиСкачать

Как найти периметр данной фигуры? Решение за одну минуту!Скачать

Графики функций с модулем | Найти площадь фигуры, заданной неравенством - 1Скачать

Найти площадь фигуры, ограниченной линиями. Пример 5.Скачать

Нахождение площадей фигур, ограниченных графикамиСкачать
Геометрический смысл определенного интеграла (2)Скачать

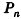
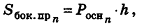
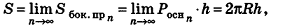
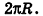
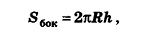
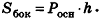
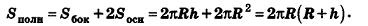

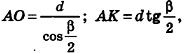
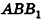
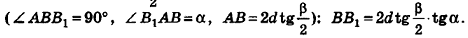
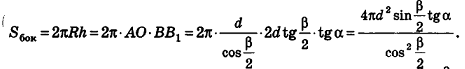
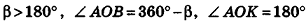
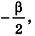
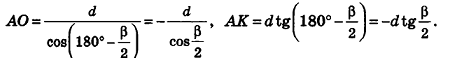
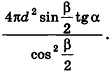
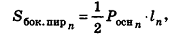
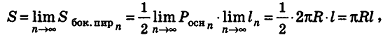
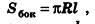
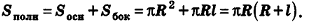
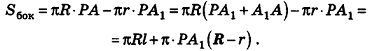
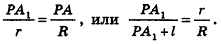
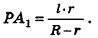
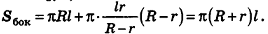
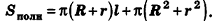
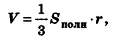
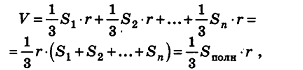
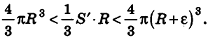
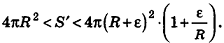
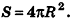
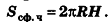
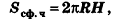






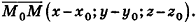
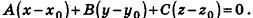
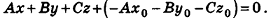
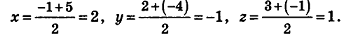
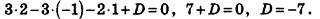
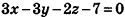
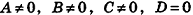 , уравнение плоскости примет вид Ax+By+Cz = 0; очевидно, что такая плоскость проходит через начало координат (рис. 234, а);
, уравнение плоскости примет вид Ax+By+Cz = 0; очевидно, что такая плоскость проходит через начало координат (рис. 234, а);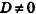 , плоскость параллельна одной из координатных осей: например, при условии А = 0 вектор нормали
, плоскость параллельна одной из координатных осей: например, при условии А = 0 вектор нормали 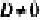 , плоскость параллельна одной из координатных плоскостей: например, при условиях А = 0 и В-О вектор нормали
, плоскость параллельна одной из координатных плоскостей: например, при условиях А = 0 и В-О вектор нормали 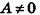 и В = С = D = 0 уравнение плоскости имеет вид Ах = О, или х= 0, то есть является уравнением плоскости Оуz (рис. 234, г).
и В = С = D = 0 уравнение плоскости имеет вид Ах = О, или х= 0, то есть является уравнением плоскости Оуz (рис. 234, г).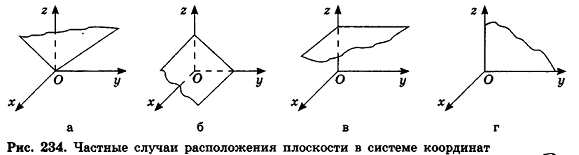
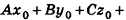
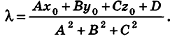
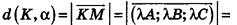
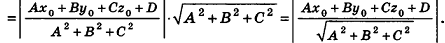
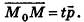
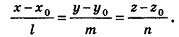
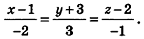
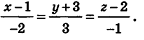
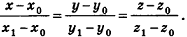
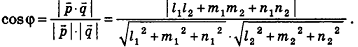
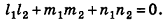
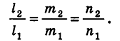
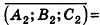
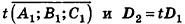 , или, если числа
, или, если числа 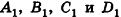 ненулевые
ненулевые 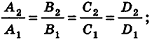
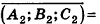
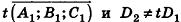 , или, если координаты
, или, если координаты 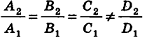 (на практике это означает, что уравнения данных плоскостей можно привести к виду Ax+By+Cz+D1= 0 и Ax+By+Cz+D2=0, где
(на практике это означает, что уравнения данных плоскостей можно привести к виду Ax+By+Cz+D1= 0 и Ax+By+Cz+D2=0, где 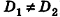 ).
).