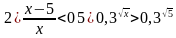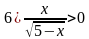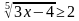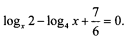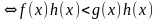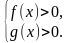План конспект урока по алгебре 10 класс алимов равносильные уравнения и неравенства

Тип урока: урок закрепления знаний.

Видео:Алгебра 10 класс (Урок№19 - Равносильные уравнения и неравенства.)Скачать

Скачать:

Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Предварительный просмотр:

Конспект урока по алгебре за 10 класс по теме: «Решение систем показательных уравнений и неравенств»

• научиться решать показательные уравнения и неравенств;
• научиться решать системы показательных уравнений и неравенств;

• развивать навыки логического мышления;
• развивать навыки вычисления.

• воспитывать внимательность и аккуратность.
• воспитывать самостоятельность и устойчивый интерес к предмету.

Тип урока: урок закрепления знаний.

Формы работы учащихся: фронтальный опрос.

Литература: «Алгебра 10-11», Учебник. Алимов Ш.А. и др.

Организационный момент (2 минуты);

Проверка домашней работы;

Актуализация знаний (5 минут);

Решение задач (34 минуты);

Подведение итогов (2 минуты);

Домашнее задание (2 минуты).

Организационный момент (2 минуты).

Приветствие учеников. Проверка готовности учащихся к уроку: проверка наличия тетрадей, учебников. Проверка отсутствующих на уроке.

Проверка домашней работы.

Проверка домашней работы происходит в том случае, если у многих учеников возникли вопросы при ее решении.

Актуализация знаний (5 минут).

Учитель. На прошлых уроках мы познакомились с понятием показательной функции, научились решать показательные уравнения, неравенства и системы показательных уравнений и неравенств, так давайте вспомним, что называется показательной функцией?

Ученик. Показательной функцией называется функция y=ах, где а заданное число, а > 0, а ≠ 1.

Учитель. Какова область определения функции y=0,3x?

Ученик. Область определения данной функции все действительные числа.

Учитель. Каково множество значения функции y=3x?

Ученик. Множество значений данной функции – действительные положительные числа.

Учитель. При каком условии показательная функция является возрастающей?

Ученик. Функция будет являться возрастающей, если а > 1.

Учитель. При каком условии показательная функция является убывающей?

Ученик. Функция будет являться убывающей, если 0

Учитель. Возрастает или убывает функция у=0,5 х и почему?

Ученик. Даная функция убывает, так как основание данной функции меньше единицы.

Учитель. Возрастает или убывает функция у=2 х и почему?

Ученик. Даная функция возрастает, так как основание данной функции больше единицы.

Учитель. Определите при каком значении а функция у=а х проходит через точку А(1; 2)?

Ученик. Функция у=а х будет проходить через точку А(1; 2) при а = 2.

Учитель. Какие способы решения показательных уравнений вы знаете?

Ученик. Приведение к одному основанию, вынесение общего множителя за скобки, введение новой переменной.

Учитель . Какие методы мы использовали для решения показательных уравнений и неравенств?

Ученик . Для решения показательных уравнений и неравенств мы использовали графический и аналитический методы.

Учитель . Что означает решить систему уравнений?

Ученик . Решить систему уравнений – значит найти все те значения неизвестной при которых каждое уравнение этой системы обращается в верное равенство.

Учитель . Что означает решить систему неравенств?

Ученик . Решить систему неравенств – значит найти все те значения которые удовлетворяют каждому неравенству этой системы.

Решение задач (34 минут).

Учитель . Запишите в тетради число, классная работа, тема урока – решение систем показательных уравнений и неравенств.

Запись на доске и в тетрадях:

Решение систем показательных уравнений и неравенств

На прошлом уроке вы научились решать системы показательных уравнений и неравенств, сегодня мы постараемся укрепить ваши знания, умения и навыки по этой теме. Поэтому сразу приступим к решению упражнений по теме. Решим систему из номера №241 под цифрой 2. Прочитайте задание.

Ученик. Решите систему уравнений.

Запись на доске и в тетрадях

Что необходимо для того чтобы решить систему уравнений?

Для того, чтобы решить систему уравнений необходимо найти все те значения неизвестных при которых каждое уравнение этой системы обращается в верное равенство.

Каким способом будем решать показательные уравнения?

Для того чтобы решить показательные уравнения приведем обе части уравнений к одинаковым основаниям.

В левой части второго уравнения мы имеем произведение степеней с одинаковым основанием, как можно преобразовать это выражение?

По свойству степеней левую часть второго уравнения можно представить в виде 3 6х+у .

И левая и правая части наших уравнений имеют в основании одно и то же число, в соответствии с этим, как можно преобразовать систему?

Так как и в левой и в правой части уравнений степени с одинаковым основанием, то мы имеем право избавиться от оснований степеней, и приравнять их показатели.

Мы получили систему уравнений с двумя переменными. Каким методом будем решать данную систему?

Для решения данной системы уравнений необходимо воспользоваться методом подстановки.

Как применим этот метод к нашей системе уравнений?

Для того чтобы решить систему уравнений методом подстановки необходимо:

1. из второго уравнения выразить у.

1. у = 3 – 6х

1. полученное выражение подставим в первое уравнение и решим полученное выражение.

1. 3х – 2 (3 – 6х) = 4

1. Подставляем найденное значение х во второе уравнение и находи значение у.

1. у = 3 – 6 * 2/3

Ответ записывается парой чисел (х; у).

Учитель. Решим систему из номера №242 под цифрой 2. Прочитайте задание.

Ученик. Решите систему уравнений.

Запись на доске и в тетрадях

Что необходимо для того чтобы решить систему уравнений?

Для того, чтобы решить систему уравнений необходимо найти все те значения неизвестных при которых каждое уравнение этой системы обращается в верное равенство.

В обоих уравнениях степени с одинаковыми основаниями и показателями, но разными знаками. Каким способом будем решать данную систему?

Для того чтобы решить данную систему необходимо сложить оба уравнения.

У нас получилось показательное уравнение, в правой части которого сумма степеней с одинаковым основанием. Каким способом следует воспользоваться для решения этого уравнения?

Так как получилось показательное уравнение в правой части которого сумма степеней с одинаковыми основаниями, необходимо вынести общий множитель за скобки.

Далее задание решается по аналогии.

Остальные задачи решаются по аналогии.

Учитель. Решим систему из номера №244 под цифрой 1. Прочитайте задание.

Ученик. Решите систему.

Запись на доске и в тетрадях

Что необходимо для того чтобы решить систему?

Для того, чтобы решить систему необходимо найти все те значения неизвестных которые удовлетворяют неравенству и при которых уравнение этой системы обращается в верное равенство.

Так как данная система содержит как уравнение, так и неравенство, то применить какой-либо известный способ решения систем мы не можем, а значит что мы должны сделать для решения данной системы?

Для решения данной системы мы должны отдельно решить уравнение и неравенство, а затем выделить те значения неизвестной, которые удовлетворяют как уравнению, так и неравенству или установить что их нет.

Для начало давайте решим неравенство. В левой части неравенства мы имеем степень с основанием 5, а в правой – число 625, можем ли мы выразить число 625 в виде степени с основанием 5?

Да, можно. 625 можно представить как 5 4

В основании степеней число 5, а 5 > 1. Как данный факт применим к решению нашего неравенства?

Так как 5 > 1, то по свойству показательных функций у = 5 2х + 1 будет являться возрастающей функцией, то решением неравенства 5 2х + 1 > 5 4 будут являться числа удовлетворяющие неравенству 2х + 1 > 4.

Показательное уравнение входящие в состав нашей системы и в правой и в левой части имеет одно и тоже основание – 11. Как данный факт применим к решению нашего уравнения?

Так как и в левой и в правой части показательного уравнения находятся степени с одинаковым основанием, то от оснований можно избавиться и приравнять их показатели. Далее решаем полученное квадратное уравнение.

6х 2 – 10х = 9х – 15

6х 2 – 19х + 15 = 0

Какие числа удовлетворяют решению данной системы?

Так как 3,(3) > 1,5 и 3 > 1,5, то оба эти числа будут являться решением системы.

Ответ: х 1 = 3,(3) и х 2 = 3

Ответ: х 1 = 3,(3) и х 2 = 3

Подведение итогов (2 минуты).

Учитель. Сегодня мы с вами продолжили решать системы показательных уравнений и неравенств. Вспомнили, как решаются отдельно друг от друга показательные уравнения и неравенства. Вспомнили, как решать системы. На следующем уроке мы вспомним материал по изученной главе, подготовимся к контрольной работе.

Все кто сегодня работал молодцы.

Домашнее задание (2 минуты).

Учитель. Дома вам необходимо повторить параграф 14, решить №243-244 (нечетные).

Запись на доске и в дневниках:

Параграф 14, №243-244 (нечетные).

Учитель. Урок окончен, можете быть свободны.

Видео:Равносильность уравнений и неравенств. Видеоурок 7. Алгебра 10 классСкачать

По теме: методические разработки, презентации и конспекты

План-конспект урока по алгебре 7 класс по теме:Решение задач с помощью систем уравнений

Открытый урок для 7 класса по алгебре по теме «Решение задач с помощью систем уравнений» подготовленный для методической недели в школе № 1462 на 19 апреля 2013 года.

План-конспект урока по алгебре в 7 классе по теме: «Решение систем линейных уравнений»

Методическая разработка урока по алгебре в 7 классе с использованием ЭОР и ссылками на мультимедийные ресурсы.

Конспект урока алгебры в 7 классе на тему «Решение систем линейных уравнений способом подстановки»

Урок изучения нового материала с применением новых обучающих структур.

Конспект урока алгебры 8 класс по теме «Решение систем линейных неравенств»

Конспект урока алгебры 8 класс по теме «Решение систем линейных неравенств» с приложением презентации в программе SmartNotebook.

Технологическая карта урока математики в 7 классе по теме «Решение систем линейных уравнений с двумя неизвестными»

Конспект урока по математике в 7 классе по теме «Решение систем линейных уравнений с двумя неизвестными» в виде технологической карты. Данный материал будет интересен учителям математики, использующим.

открытый урок по алгебре 8 класс на тему «Решение систем неравенств с одной переменной»

открытый урок по алгебре 8 класс на тему «Решение систем неравенств с одной переменной» Урок полностью соответствует ФГОС+ презентация к уроку.

Конспект урока по алгебре 8 класс по теме «Решение неравенств с одной переменной»

урок изучения нового материала с применением ЭОР.

Видео:Алгебра 10 класс // Логарифмы // Контрольная работа // Решение, ответы // К учебнику АлимоваСкачать

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №19. Равносильные уравнения и неравенства

Перечень вопросов, рассматриваемых в теме

1) понятие равносильного уравнения;

2) понятие равносильного неравенства;

3) понятие уравнения-следствия;

4) основные теоремы равносильности.

Глоссарий по теме

Два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней.

Если при переходе от одного уравнения к другому потери корней не происходит, то второе уравнение называет следствием первого уравнения. Иначе, если все корни первого уравнения являются корнями второго уравнения, то второе уравнения называется следствием первого уравнения.

Неравенства, имеющие одно и то же множество решений, называют равносильными. Неравенства, не имеющие решений, также являются равносильными.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Определение. Два уравнения с одной переменной

f(х) = g(х) и р(х) = h(х) называют равносильными, если множества их корней совпадают.

Иными словами, два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней.

1) Уравнения равносильны, т.к. каждое из них имеет только один корень х=3.

2) Уравнения также равносильны, т.к. у них одни и те же корни .

3) А вот уравнения не равносильны, потому что у первого уравнения корень х=2, а у второго уравнения два корня х=2 и х=-2.

Из определения равносильности следует, что два уравнения равносильны, если каждый корень первого уравнения является корнем второго уравнения, и наоборот.

Решение уравнения осуществляется в три этапа.

Первый этап — технический. На этом этапе осуществляют преобразования по схеме (1) → (2) → (3)→ (4) → . и находят корни последнего (самого простого) уравнения указанной цепочки.

Второй этап — анализ решения. На этом этапе, анализируя проведенные преобразования, отвечают на вопрос, все ли они были равносильными.

Третий этап — проверка. Если анализ, проведенный на втором этапе, показывает, что некоторые преобразования могли привести к уравнению-следствию, то обязательна проверка всех найденных корней их подстановкой в исходное уравнение.

Реализация этого плана связана с поисками ответов на четыре вопроса.

• Как узнать, является ли переход от одного уравнения к другому равносильным преобразованием?
• Какие преобразования могут перевести данное уравнение в уравнение-следствие?
• Если мы в конечном итоге решили уравнение-следствие, то как сделать проверку в случае, когда она сопряжена со значительными вычислительными трудностями?
• В каких случаях при переходе от одного уравнения к другому может произойти потеря корней и как этого не допустить?

Из курса средней школы мы знаем, что можно сделать следующие преобразования уравнений: любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный.

Обе части уравнения можно умножить или разделить на одной и то же число, не равное нулю.

Если при переходе от одного уравнения к другому потери корней не происходит, то второе уравнение называет следствием первого уравнения. Иначе, если все корни первого уравнения являются корнями второго уравнения, то второе уравнения называется следствием первого уравнения.

Из этого определения и определения равносильности уравнений следует, что:

1. если ва уравнения равносильны, то каждое из них является следствием другого;
2. если каждое из двух уравнений является следствием другого, то эти уравнения равносильны.

При решении уравнений главное- не потерять корни, а наличие посторонних корней можно установить проверкой. Поэтому важно следить за тем, чтобы при преобразовании уравнения каждое следующее уравнение было следствием предыдущего.

Стоит отметить, что посторонние корни могут получиться при умножении обеих частей уравнения на выражение, содержащее неизвестное; а вот потеря корней может произойти при делении обеих частей уравнения на выражение, содержащее неизвестное.

Итак, сформулируем основные теоремы, которые используются при решении равносильных уравнений:

Определение. Областью определения уравнения f(х) = g(х) или областью допустимых значений переменной (ОДЗ) называют множество тех значений переменной х, при которых одновременно имеют смысл выражения

Теорема 1. Если какой-либо член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение, равносильное данному.

Теорема 2. Если обе части уравнения возвести в одну и туже нечетную степень, то получится уравнение, равносильное данному.

Теорема 3. Показательное уравнение (где а > 0, a≠1)

равносильно уравнению f(x) = g(х).

Теорема 4. Если обе части уравнения f(x) = g(х) умножить на одно и то же выражение h(х), которое:

а) имеет смысл всюду в области определения (в области допустимых значений) уравнения f(x) = g(х)

б) нигде в этой области не обращается в 0, то получится уравнение f(x)h(x) = g(x)h(x), равносильное данному в его ОДЗ.

Следствием теоремы 4: если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Теорема 5. Если обе части уравнения f(x)=g(х) неотрицательны в ОДЗ уравнения, то после возведения обеих его частей в одну и ту же четную степень n получится уравнение равносильное данному в его ОДЗ.

Краткая запись теорем 4, 5.

4. f(x) = g(x) ⇔h(x)f(x) = h(x)g(x), где h(x) ≠0

и h(x) имеет смысл в ОДЗ данного уравнения.

5. f(x) = g(x) ⇔ , где f(x)≥0, g(x)≥0

и n=2k (чётное число).

Например, х – 1 = 3; х = 4

Умножим обе части на (х – 2):

(х – 2)(х – 1) = 3(х – 2); х = 4 и х = 2 – посторонний корень⇒ проверка!

Равносильность неравенств с неизвестным определяется аналогично.

Неравенства, имеющие одно и то же множество решений, называют равносильными. Неравенства, не имеющие решений, также являются равносильными.

Разбор решения заданий тренировочного модуля

Решим уравнение:

Возведем в квадрат обе части уравнения, получим:

, которое не будет равносильно исходному уравнению, потому что у этого уравнения два корня , а у первоначального уравнения только один корень х=4.

1. Неравенства и x-3 x-1 не равносильны, так как решениями первого являются числа x 1, а решениями второго- числа x>-1. При решении неравенств обычно данное неравенство преобразуется в ему равносильное.

Видео:Алгебра 10 класс (Урок№1 - Числовые и алгебраические выражения. Линейные уравнения и неравенства.)Скачать

Конспект урока «Равносильность неравенств»

1. Организационный момент
2. Постановка цели и задач урока
3. Актуализация опорных знаний и их коррекция:

а) математический диктант, работа по карточкам;

б) повторение теоретических сведений по изучаемой теме, проверка домашнего задания.

4) Изучение и закрепление материала:

а) равносильность неравенств;

б) системы и совокупности неравенств.

5) Рефлексия. Подведение итогов урока

6) Домашнее задание

Просмотр содержимого документа
«Конспект урока «Равносильность неравенств»»

Тема урока: «Равносильность неравенств»

— формировать навыки равносильных переходов при решении неравенств, их коррекция и

— создавать условия для закрепления, повторения и углубления знаний.

ввести понятие равносильности неравенств, рассмотреть теоремы равносильности,

рассмотреть примеры равносильных переходов при решении неравенств с одной переменной;

закрепить умение применять основные теоремы равносильности при решении неравенств с одной переменной;

способствовать расширению знаний по изучаемой теме;

развитие логического мышления, познавательного интереса;

формирование математической речи, умения анализировать и сравнивать, делать выводы;

развитие навыков работы над проектами;

развитие приемов умственной деятельности, умения искать рациональный способ решения поставленной задачи;

повышение информационной культуры учащихся, интереса к предмету;

развитие потребности к самообразованию, умение вырабатывать собственную позицию (обосновывать свой решения, свой результат);

обучение эстетическому оформлению записи в тетради и на доске,

воспитание ответственности, самостоятельности, умения работать в коллективе;

обучение умению выступать перед аудиторией и выслушивать других;

повышать уровень учебной мотивации с использованием компьютерных технологий;

воспитание уважения друг к другу, коллективизма, взаимопомощи и ответственности за общую работу.

-компьютер, экран, проектор для показа презентаций, раздаточный материал по теме урока, буклеты.

Постановка цели и задач урока

Актуализация опорных знаний и их коррекция:

а) математический диктант, работа по карточкам;

б) повторение теоретических сведений по изучаемой теме, проверка домашнего задания.

4) Изучение и закрепление материала:

а) равносильность неравенств;

б) системы и совокупности неравенств.

5) Рефлексия. Подведение итогов урока

6) Домашнее задание

1) Организационный момент

Приветствие учащихся, проверка готовности к уроку, вступительное слово учителя, название темы, запись в тетрадях числа и темы урока (слайд 1)

2) Постановка цели и задач урока

Ребята, я предлагаю сегодня на уроке привести в систему знания и расширить представление о равносильности неравенств. Дьёрдь По́йа сказал: «Недостаточно лишь понять задачу, необходимо желание решить её. Где есть желание, найдется путь!» А я уверена, что у вас есть желание узнать новое, анализировать, делать выводы, найти свой путь решения и расширить знания, которые вам понадобятся для успешной сдачи ЕГЭ. Учитель вместе с учащимися формулирует цели и задачи урока. Здесь мы сначала дадим определение равносильных неравенств и приведем примеры. Дальше перечислим основные виды равносильных преобразований неравенств и докажем их. А в заключение выясним, почему при решении неравенств нужно использовать только равносильные преобразования.

3)Актуализация опорных знаний и их коррекция

а) Математический диктант, работа по карточкам

Математический диктант (слайд 2):

Запишите ответы к неравенствам (слайд 3):

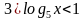
По окончании проверка осуществляется в парах по ответу: (0; 5) (слайд 4)

Во время диктанта трое учащихся работают у доски по карточкам

Решите уравнение 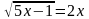. Если уравнение имеет более одного корня, в ответе укажите меньший из них.

Решите неравенство 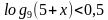. В ответе укажите количество целых решений

1.Решите неравенство (3х+15) 2 2

2.Решите неравенство

б) Повторение теоретических сведений по изучаемой теме, проверка домашнего задания

— работа по домашнему заданию, проверка заданий учениками, вызвавших затруднения;

— вспоминают определение решения неравенства, частного и общего решения неравенства

(учащиеся приводят примеры решений).

Решением неравенства называется всякое действительное значение неизвестного, при котором неравенство справедливо. Решить неравенство — значит найти множество всех его решений. Это множество может оказаться пустым, т. е. существуют неравенства, которые не имеют решений.

Изучение и закрепление материала

а) Равносильность неравенств

Выполнение некоторых действий с правой и/или левой частью неравенства или с их отдельными слагаемыми может давать новые неравенства, имеющие те же решения, что и исходное неравенство. Замену исходного неравенства на новое равносильное ему неравенство при помощи таких действий назвали равносильным преобразованиям неравенства. Равносильное преобразование неравенства – это его замена другим равносильным ему неравенством, то есть, неравенством, имеющим то же множество решений. Сами преобразования, приводящие к равносильному неравенству, также называют равносильными преобразованиями.

Возникает логичный вопрос: «Зачем вообще нужны эти равносильные преобразования неравенств»? Например, они позволяют решать неравенства: с их помощью от решения исходного неравенства можно перейти к решению более простого, но равносильного неравенства (далее учащиеся записывают определения в тетради).

Определение1. Два неравенства с одной переменной f(x)g(x) и p(x)h(x) называют равносильными, если их решения совпадают.

Определение2. Если общее решение неравенства f(x)g(x) содержится в общем решении неравенства p(x)h(x), то второе неравенство называют следствием первого (слайд 5).

Например (слайд 6):

х 2 9 –это неравенство — следствие неравенства 2х6.

Теперь можно перейти к знакомству с основными и наиболее часто используемыми равносильными преобразованиями неравенств, которые иногда называют свойствами неравенств. Им стоит уделить должное внимание – без их использования не обходится решение почти ни одного неравенства. Заметим, что они похожи на равносильные преобразования уравнений. Принцип их доказательства тоже аналогичен, только здесь в основе доказательства будут лежать, естественно, свойства числовых неравенств, а не свойства числовых равенств.

Итак, приступим (учащиеся записывают краткие формулировки теорем) .

Теорема1. Если какой-либо член неравенства перенести из одной части неравенства в другую с противоположным знаком, оставив знак неравенства без изменения, то получится неравенство, равносильное данному неравенству.

f(x)g(x) 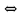f(x) — g(x)0 (слайд 7)

Прибавление (или вычитание) из обеих частей неравенства одного и того же числа является равносильным преобразованием. К примеру, оно позволяет от неравенства 3×12+5х перейти к равносильному неравенству 3x – 5х12.

Теорема 2.Если обе части неравенства возвести в одну и ту же нечетную степень, оставив знак неравенства без изменения, то получится неравенство равносильное данному.

f(x)g(x) 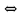(f(x)) 2n-1 (g(x)) 2n-1

Пример: 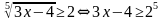(слайд 8)

Теорема 3. Показательное неравенство а f ( x ) а g ( x ) равносильно:

а) неравенству того же смысла f(x)g(x), если а1,

б) неравенству противоположного смысла f(x)g(x), если 0

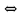
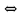
а f ( x ) а g ( x ) f(x)g(x), если а1 и а f ( x ) а g ( x ) f(x)g(x), если 0

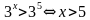
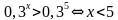
Примеры: и (слайд 9)

Теорема4.а)Если обе части неравенства f(x)g(x) умножить на одно и то же выражение h(x), положительное при всех х из области определения неравенства f(x)g(x), оставив при этом знак неравенства без изменения, о получится неравенство f(x) h(x)g(x) h(x), равносильное данному.

б) Если обе части неравенства f(x)g(x) умножить на одно и то же выражение h(x), отрицательное при всех х из области определения неравенства f(x)g(x), изменив при этом знак неравенства на противоположный, то получится неравенство f(x) h(x)g(x) h(x), равносильное данному.

Если h(x)0 на ОДЗ неравенства f(x)g(x), то f(x)g(x)

Если h(x)f(x)g(x), то f(x)g(x)

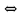
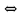
Примеры: 2х4 х2 и х(-х 2 -1) -х 2 -1 х

Теорема5.Если обе части неравенства f(x)g(x) неотрицательны в области его определения, то после возведения обеих частей неравенства в одну и ту же четную степень получится неравенство того же смысла (f(x)) 2 n (g(x)) 2 n , равносильное данному в его ОДЗ.

Если f(x)≥0 и g(x)≥0, то f(x)g(x)⇔ (f(x)) 2 n (g(x)) 2 n

Пример: х 2 ≥9⇔х≥3 при х≥0 (слайд11)

Теорема 6. Пусть Х – решение системы неравенств

Тогда логарифмическое неравенство 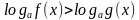равносильно на множестве Х:

а) неравенству того же смысла f(x)g(x), если а1,

б) неравенству противоположного смысла f(x)g(x), если 0

Пример: ,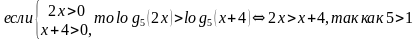

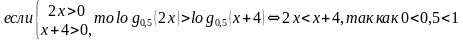
(слайд12)

Замена выражения в левой и/или правой части неравенства тождественно равным выражением на области допустимых значений (ОДЗ) переменных исходного неравенства является равносильным преобразованием неравенства.

Отдельно подчеркнем важность учета ОДЗ при замене частей неравенства тождественно равными им выражениями: если ОДЗ полученного неравенства будет отличаться от ОДЗ исходного неравенства, то это неравенство может быть не равносильно исходному. Этот момент критически важен, он может приводить к неверным ответам при решении неравенств. Не менее важен и момент, касающийся замены на именно тождественно равное выражение

К чему приводят неравносильные преобразования неравенств? (слайд 13)

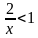
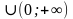
1) x−2 и — . Решением первого является промежуток (−2, +∞), а второго – (-∞; -2) .

2) и хРешением первого является промежуток (0; 5), а второго – (-∞; 5)

Вывод: Признаком возможного неравносильного преобразования неравенства является сужение или расширение ОДЗ. Наиболее часто неравносильные переходы при решении неравенств возникают при неаккуратном применении свойств корней, логарифмов и модуля. На этом мы особо заострим внимание, когда будем разбираться с решением неравенств соответствующих видов

Решим неравенство , применяя теоремы равносильности

Ответ: [1; 2] ) (слайд 14). (У доски решает один из учащихся)

б) Системы и совокупности неравенств

Определение3. Говорят, что несколько неравенств с одной переменной образуют систему неравенств, если ставится задача найти все одинаковые частные решения заданных неравенств. Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называют частным решением системы неравенств. Множество всех частных решений системы неравенств называют решением системы неравенств.

Решение системы неравенств представляет собой пересечение решений неравенств, образующих систему (неравенства записывают, объединяя вместе фигурной скобкой).

Пример: Решите систему неравенств. (Ответ: )) (слайд16)

Определение4. Говорят, что несколько неравенств с одной переменной образуют совокупность неравенств, если ставится задача найти все такие значения переменной, каждое из которых является частным решением хотя бы одного из заданных неравенств. Каждое такое значение переменной называют частным решением совокупности неравенств. Множество всех частных решений совокупности неравенств называют решением совокупности неравенств.

Решение системы неравенств представляет собой объединение решений неравенств, образующих совокупность (неравенства записывают, объединяя вместе квадратной скобкой).

Пример: Решите совокупность неравенств. (Ответ: )) (слайд 17)

Работа по учебнику — №28.39(б) (У доски решает один из учащихся)

5) Рефлексия. Подведение итогов урока

Понятно, что, кроме равносильных преобразований неравенств, есть и неравносильные, от которых, решая неравенства, нужно держаться подальше. А дело здесь в том, что, выполнив переход к неравносильному неравенству, можно получить решение, которое не является искомым решением исходного неравенства. В некоторых случаях можно получить и верный ответ, но это будет не более чем везение, а в общем случае, выполняя неравносильные преобразования неравенств, будет получен неверный ответ.

Вывод ясен: при решении неравенств нужно выполнять только равносильные преобразования.

При обобщении изученного материала обучающие отвечают на вопросы:

Что нового было на уроке?

Больше всего затруднений вызвало…

Для меня непонятно было… (слайд18)

6) Домашнее задание

По учебнику решить — №28.1(б), 28.3(б,в), 28.10(б), 28.12(в), 28.41(б), 28.49 (а) (слайд 19)

Творческое задание для группы учащихся – привести примеры к каждому определению и теореме и сделать презентацию.

🎬 Видео

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

10 класс, равносильные уравненияСкачать

Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать

№ 11 ГДЗ по алгебре 10 класс Алимов | выражения с квадратным коренемСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Показательная функция | 10 класс АлимовСкачать

№ 9 ГДЗ по алгебре 10 класс Алимов | иррациональные числаСкачать