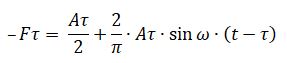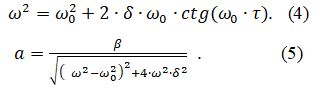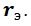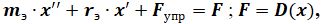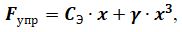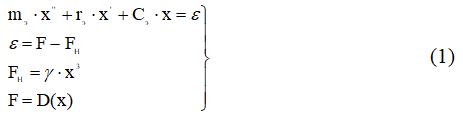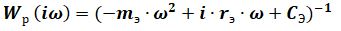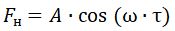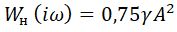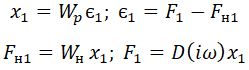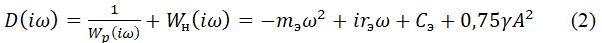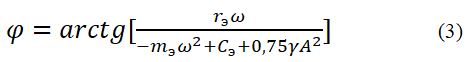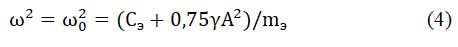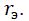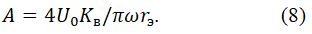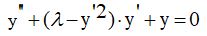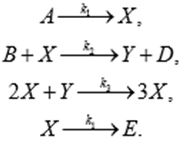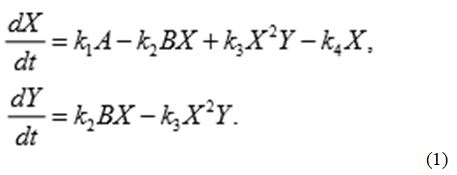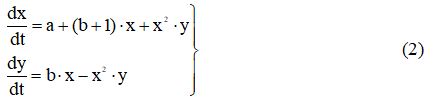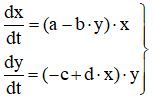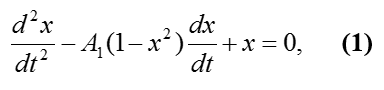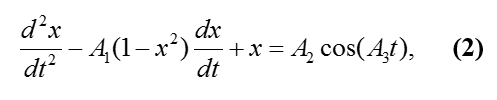
Питон уравнение ван дер поля (3 видео)

Метод медленно меняющихся амплитуд (метод Ван-дер-Поля)

Содержание

Метод медленно меняющихся амплитуд (метод Ван-дер-Поля)
Автоколебания и резонанс
Здравствуйте!
Автоколебания в технике
Химические колебания. Брюсселятор
Автоколебания в биосистемах (на примере модели Лотки Вольтерра –“Хищник -жертва”)
Питон уравнение ван дер поля
🎬 Видео

Видео:34 Задача: Найти корни квадратного уравнения при помощи PythonСкачать

Метод медленно меняющихся амплитуд (метод Ван-дер-Поля)

Этот метод полезен, когда движение материальной системы описывается дифференциальным уравнением с малой нелинейностью. Х А х я i. 4. Где f x, i -нелинейная функция x и, А p-малый параметр. если f x, f 0, то уравнение 4 будет линейным I A x 0, общее решение которого, как известно х asln Ш А, х aAcos а а. В 1926 году Ван дер Поль предложил, что для малой нелинейности общее решение Формулы 4 и ее первая производная имеют внутренний индекс, соответствующий линейному уравнению 2×0. х грех т а, я Ак COS в т а, 5 Где амплитуда а и начальная фаза а-медленно меняющиеся функции времени а а 0, х х 0. Этот метод позже Л. И. Мандельштама и N. D.

Было продемонстрировано математически в исследовании папалекси. Мы видим, что это нелинейное дифференциальное уравнение 2-го порядка 4 эквивалентно 2 нелинейным дифференциальным уравнениям 1-го порядка. a j — asinij , ak cos , a — asinifi, ak cos , где вводится обозначение. Вместо этих точных уравнений было предложено закрепить приближение-уравнение, полученное из укороченного 6, заменив правую часть соответствующей средней величиной в диапазоне от 0 до 2, то есть правой стороной. 2р Если а 2 ф asinTf, аль cosxj з-рН, 7 2р a — a slnф cosФ sln 4 8 При вычислении правых интегралов этих приближенных нелинейных уравнений амплитуда a должна считаться постоянной.

При вычислении момента инерции однородного трехмерного твердого тела относительно некоторой оси выделяют в твердом теле-такой элементарный объем, момент инерции которого относительно соответствующей оси известен, либо легко может быть определен. Людмила Фирмаль

Интегралы дифференциальных уравнений свободных колебаний с малыми нелинейностями методом ван дер поля рекомендуется выполнять в следующем порядке 1 Создайте дифференциальное уравнение свободной вибрации и запишите его в виде 4. 2 взять x a sin f, x aAcosif и вычислить определенный интеграл 2-й 2-й Дж. Ф. грех доктора, Ак sovf sovf Ф, asinty, Ак cosф sinф ф При рассмотрении константы 3 Добавить результат предыдущего абзаца справа от укороченного уравнения ван дер поля 7 и 8. 4 интегрируйте уравнение 7 и вычислите полное интегрирование Ф, ст 5 присвоить полученные значения a t, Cj укороченному дифференциальному уравнению 8 и интегрировать его, вычисляя общий Интеграл a a f, Cb C9.

Подставляя полученные значения a t, Cj и a t, Cy Ca в уравнение 5, определить начальное условие заданного движения 0, x x0, I интегральная константа C 7 полученные значения Ci и Ca вычисляются в пунктах a A Z, Cj и a a т. е. если вы хотите добавить к нему значение, вам нужно добавить его в Cy Cg. 4 и 5 8 подставляя искомое уравнение движения О грехе А М Значения a t и a , полученные в предыдущем пункте. Задача 20.3.Решите задачу 20.2, используя метод медленного изменения амплитуды. Решение.

Напишите рассматриваемое дифференциальное уравнение 4 20.2 по форме Ф 2е р р 1 2 Найти решение в виде Формулы 1 и ее производных первого порядка Ф ж грех В а т, ф А А Т, потому что Т А я Джей 3 Где переменная амплитуда в 0 и переменная начальная фаза а 0 являются предметом последующего определения. Если сравнить уравнения 1 и 4, приведенные в обзоре теории, то в этом случае x p Ф. ф ф СР a sin , и P aAsozph аз nf, а A cos f a s1a f. 4 0 и 0, предварительное вычисление определенных интегралов 2р 2р м НП, aAco5p Софья 7п и J a81pf, aAco8p 81pf1 Ф 4 в предположении, что существует и величина а постоянна Ф грех Ф Ак со Ф соз ф ф А Й грех Ф со Ф Ыф 2л 2л J A sin , ak cos sin a J sin.

Если использовать подстановку sfnif z с первым интегралом b , а во 2-м Интеграле 5 с выражением sin ij — —soz2p at sob4p Второй Дж. Ф. Син Ф Ак со Ф соз Ф с ф 0 2л Ф А sin , Ак при cos sin — — Ла. 6 Вводя значение интеграла 6 в укороченное уравнение ван дер поля 7 и 8, приведенное в обзоре теории и рассматривая 2 а 0, д 7 Из первого выражения 7 е 0-ср. 8 Если вы присваиваете 8 2 — му выражению 7, то оно имеет вид a — AC .Когда вы интегрируете Подставляя результаты 8 и 9 в Формулу 3, можно найти -C,, 1n 4 1- C С, , 10 4.-4C1eo1 я л-ЛК с,. 11 В 10 0, p a0, 11 вводя t 0, p 0, получаем систему уравнений a0 ClsinC2l 0 ZrCj cos Sc.

Если вы решите эту систему, у вас будет Ci a0, Ct n 2, если Cj 0, то решение системы будет потеряно вообще. Подставляя полученные значения Cx и Ca в 10, находим искомое уравнение для колебаний маятника. Ф conv convl 1 — 12 Как видно из 12, круговая частота p колебаний маятника, согласно его начальному угловому отклонению a0 — — ..И 13 Если мы решим уравнение 12 и результат задачи 20.2 21 способом, расширяющимся с малыми параметрами, мы увидим, что метод ван дер поля производит первый первичный член уравнения 21 задачи с несколько меньшим вычислительным весом. Оказывается, что размер циркулирующей частоты p, найденный двумя способами, одинаков см.

Уравнение в вопросе 20.2 13 и уравнение 20. Поэтому применение метода ван дер поля для определения первого приближения должно считаться целесообразным и эффективным. Задание 20.4.Материальная точка массы m движется вдоль оси x под действием упругих сил и сопротивления. Его проекция Fx — ex, Rx — Pi — Pz — 3, соответственно. C Pi и Pz положительны constants. At начальная точка, точка находилась в крайнем положении, определяемом координатой x od, и была выпущена без начальной скорости. Найти уравнение движения точки с помощью метода ван дер поля. Решение. Дифференциальное уравнение движения точки mX Fx Rx.

Затем определяется искомый момент инерции однородной плоской фигуры путем суммирования моментов инерции всех элементарных площадей. Людмила Фирмаль

Для конкретных значений Fx и Rx ТХ — СХ-видеорегистратор PTX-Pax3, или Х х — р а-P3X3, 1 Ниже эта задача решается эквивалентным методом линеаризации задача 20.5 с сравнительной оценкой различных решений. Вот, кг с m, 2ni fiilm, n 3, m, 1 И л положительны. Мы ищем решение Формулы 1 x и ее первой производной, A, в виде х а 0 грех а 4- х 0,а аа 0 потому что а 2 Где a и a — переменная амплитуда и начальные фазы, которые подлежат последующим решениям. Если сравнить уравнения 1 и 4, приведенные в обзоре теории, то можно сказать, что p, f x, j — la 3 найдено. asinij , Л AA cosip, пиши с sinф, Ак cosф −2лхаАcosф-Лза А8 cosф.

Предварительно вычислите определенный интеграл, чтобы найти и t 2р 2л J p az1pf, и a cos f cos f b f, c a81pf, ak cosf sin f t f, учитывая уравнение 3, в предположении, что A-постоянная 5 часов вечера b81pf, fl A COS f COS f b f — 2л А. Дж коза ф т ф-Lzd А3 Дж Коза Ф УГ, 4 с a81pf, Ак со Ф грех ф т ф −2 ща Дж cosфsinфсГф-л8а3А3 cos3фsinфф ф.

Формула, используемая при вычислении интеграла 4 потому что ф у Я cos2ф, cos1ф А cos2ф 1 cos4ф И если вы присваиваете SOF x интегралу 5 2р Джей с ф грех, Ак cosф cosф ф −2пп Ак-Джей nn3a3A 6 Путем введения интегралов 7 и 8 в укороченное уравнение ван дер поля 6 и 7, приведенное в обзоре теории Формула 8 Если вы разделите переменные, вы найдете r mt С другой стороны Мы пишем 8 9 У Если мы интегрируем это уравнение Иначе говоря В-в 1 л ы Ки — П Здесь Интеграл константы CI является предметом для последующих решений. решение уравнения 11 на a Интеграл уравнения 9 равен 13 Введем результаты 12 и 13 в уравнение 2. х грех м Джи — Е-Р 1. потому что Т КТ С. В.

Если подставить начальные условия i 0, x-a0 в уравнение 14 и присвоить начальные условия t 0 и jf 0 уравнению 15, то получим уравнение. После решения этой системы C4a 2, Cj V14-X2a a0..Узнайте больше. Используйте эти значения Cx и Cj для описания желаемой подгонки в следующей форме КЛ х 1аи-Ся Ле-2njl Потому что КТ.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Автоколебания и резонанс

Здравствуйте!

В связи с вопросами читателей моей публикации [1] касательно условий возбуждения автоколебаний в механической системе, я решил описать явление возникновения и поддержания автоколебаний подробно, выделив основные области возникновения и применения автоколебаний.

В википедии автоколебания объясняют так [2]:

Незатухающие колебания в диссипативной динамической системе с нелинейной обратной связью, поддерживающиеся за счёт энергии постоянного, то есть непериодического внешнего воздействия.

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы. При этом частота становится почти равной резонансной.

Автоколебания в технике

Автоколебательная система с запаздыванием (на примере электромеханического звонка)
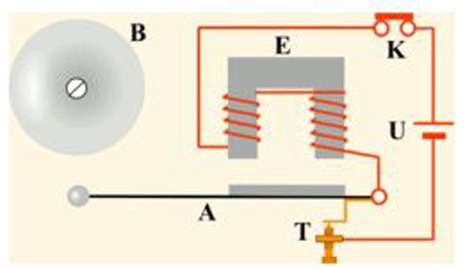
Приведём пример электромеханического звонка:

При замыкании цепи кнопкой (К) электромагнит (Е) притягивает ударник, ударник бьёт по звонку и размыкает цепь питания электромагнита, механически связанным с ним контактом (Т) ударник (А) возвращается назад и процесс повторяется.

При рассмотрении процесса возникновения автоколебаний будем считать, что сила, действующая на боёк (А) звонка, изменяется пропорционально изменению тока в RL цепи.

Такое допущение сделано для упрощения рассмотрения, поскольку зависимость силы от тока в обмотке и зазора между бойком и полюсами значительно сложнее [3].

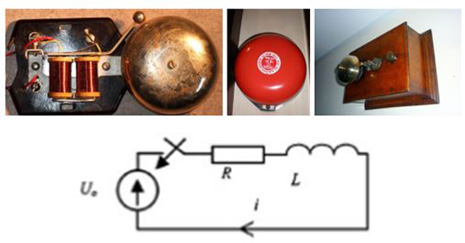
Ниже приведены конструкции электромеханических звонков и их упрощённая электрическая схема:

Боёк колеблется относительно установленного зазора согласно соотношению A*sin (w*t).
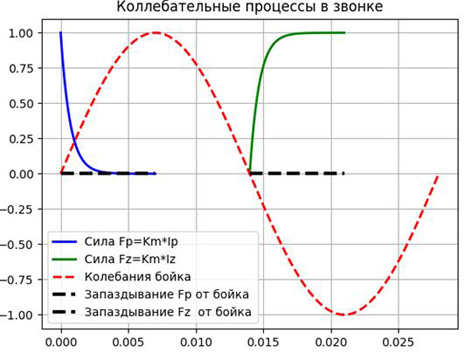
Решив численным методом дифференциальное уравнение RL цепи с начальными условиями
для замыкания и размыкания контакта, наложив на эти решения колебания бойка, получим:

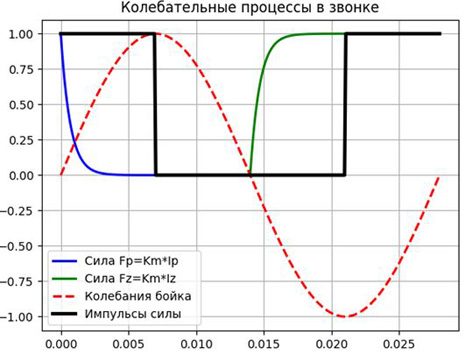
Для приближенной теории будем считать, что сила Fτ, выраженная последовательностью прямоугольных импульсов, которые возникает и исчезает мгновенно, но не в момент срабатывания контакта, а с запаздыванием τ=L/R. Добавим Fτ на график, получим:

Обозначим амплитуду силы Fτ через Aτ, получим разложения этой силы в ряд Фурье [4] (учитывая что x=a∙sin(ω∙t), для первых двух членов ряда:

Будем считать, что постоянная составляющая силы Aτ/2 компенсируется регулировкой.
Тогда уравнение для колебаний бойка с учётом его приведенной массы m, трения r и изгибной жёсткости k примет вид:

(1)

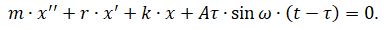
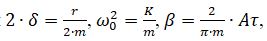
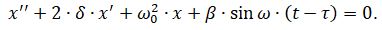
Разделим обе части на массу бойка, введем обозначения, получим:

(2)

Для того, чтобы получить аналитические соотношения для частоты и амплитуды колебаний бойка, решим (2) приближённым методом [5]. Преобразуем (2) к виду:

(3)

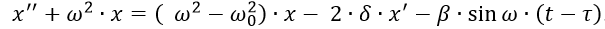
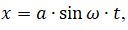
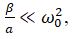
Подставив в (3) при условии:
пропуская промежуточные выкладки получим соотношения для частоты и амплитуды автоколебаний:

На основании приведенных соотношений можно сделать вывод, что, при отсутствии самоиндукции, звонок работать не может, поскольку при L=0 нет запаздывания τ=0. Таким образом, при нулевом запаздывании автоколебания не возможны.

Автоколебания в измерительной технике (на примере механического резонатора вибрационных плотномеров)

Механические резонаторы в виде трубок пластин или цилиндров широко используются в вибрационных плотномерах, внешний вид которых приведен на рисунках:

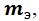
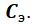
Будем рассматривать резонатор c сосредоточенными эквивалентными параметрами: массой жесткостью и трением, характеризуемым коэффициентом

Такая замена вполне допустима в ограниченной области частот при соблюдении равенства собственных частот колебаний обеих систем, а также равенства потерь энергии и обусловленных ими затуханий.

Запишем систему уравнений, описывающих движение резонатора в замкнутой системе возбуждения:

где: F- сила воздействия системы возбуждения на резонатор;
D(x)- неизвестный оператор обратной связи, подлежащий определению; Fупр — упругая восстанавливающая сила резонатора, которая в общем случае может описываться нелинейной функцией; х — поперечное смещение эквивалентной массы.

Воспользуемся выражением кубической упругой характеристики резонатора:

где γ — коэффициент, характеризующий отклонение реальной упругой характеристики от линейной.

Преобразуем записанную систему равенства к виду:

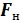
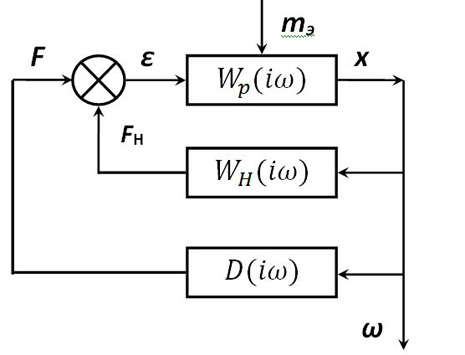
где — нелинейная составляющая упругой силы.

Структурная схема автоколебательной системы, работа которой характеризуется уравнениями, (1) приведена на рисунке:

Схема содержит нелинейное звено, выполняющее функцию корректирующей обратной связи линейного резонатора, имеющего частотную характеристику:

Для решения задачи синтеза оптимальной системы возбуждения, воспользуемся методом гармонической линеаризации [6].

Механические резонаторы являются высокодобротными колебательными системами, которые можно рассматривать как узкополосные фильтры с выходным сигналом вида: x

A∙cos⁡(ω∙τ), где A— амплитуда колебаний резонатора; ω — частота колебаний, близкая к резонансной [7].

Поэтому для нелинейного элемента справедливо соотношение:

Пренебрегая третьей гармоникой, отфильтрованной линейной частью резонатора, частотную характеристику линеаризованного звена нелинейной упругости механического резонатора можно в виде:

Рассмотрим уравнение для первой гармоники колебаний линеаризованной системы:

Для определения вида частотной характеристики D(iω), обеспечивающей совместность этой системы, исключим промежуточные переменные прямой подстановкой их выражений через другие переменные. В результате получим:

Из соотношения (2) определим смещение фазы, осуществляемое системой возбуждения:

Нетрудно установить, что частота автоколебаний не будет зависеть от трения 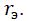при сдвиге фазы φ=π/2, тогда:

При этом условии из (2) следует, что система возбуждения должна быть дифференцирующим звеном D(iω)=(i*rэ* ω) т.е.

Из (5) следует, что частотная характеристика цепи обратной связи системы возбуждения должна быть пропорциональна коэффициенту трения

Система возбуждения состоит из трех элементов, D(iω)=Dп* Dу* D(в ), характеризующих частотные характеристики: приемника Dп, усилителя Dу и возбудителя D(в ) колебаний. Приемник является дифференцирующим – Dп=Kп* i*ω, а возбудитель усилительным
звеном – Dв=Kв.

Для выполнения условия (5) усилитель должен иметь частотную характеристику:

Коэффициент усиления должен меняться вместе с изменением трения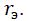
Звено с переменным коэффициентом усиления можно реализовать простейшей нелинейностью типа двухпозиционного реле, имеющей частотную характеристику по первой гармонике [6]:

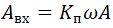
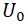
где — амплитуда первой гармоники на входе усилителя; — выходное напряжение усилителя, подаваемое на возбудитель колебаний.

Из (6) и (7) можно получить выражение для амплитуды установившихся автоколебаний резонатора:

Для устранения этого влияния амплитуды на частоту резонатора можно стабилизировать амплитуду A варьированием напряжения U0 с помощью регулятора, стабилизирующего амплитуду входного сигнала Aвх, поступающего с приемника колебаний.

Из изложенного можно сделать вывод, что частота автоколебаний резонатора вибрационного измерительного преобразователя не будет зависеть от трения при сдвиге фазы φ=π/2, когда система возбуждения является дифференцирующим звеном, и не будет зависит от амплитуды автоколебаний при стабилизации входного сигнала этого звена.

Автоколебания в радиотехнических генераторах (на примере решения уравнения
Ван-дер-Поля)

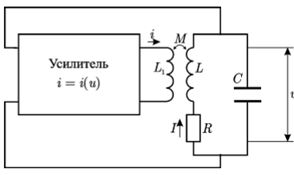
Обобщённая схема радиотехнического генератора автоколебаний приведена на рисунке:

Механизм возбуждения автоколебаний в генераторе можно качественно описать следующим образом. Даже при отсутствии напряжения на выходе усилителя напряжение в контуре испытывает случайные флуктуации. Они усиливаются усилителем и вновь поступают в контур через цепь обратной связи.

При этом из шумового спектра флуктуаций будет выделяться составляющая на собственной частоте высокодобротного контура. Если энергия, вносимая в контур таким образом, превосходит энергию потерь, амплитуда колебаний нарастает.

Основной моделью, описывающей автоколебания в радиотехническом генераторе, является уравнение Ван-дер-Поля. Приведём уравнение Ван-дер-Поля к виду, содержащему единственный управляющий параметр с безразмерными переменными:

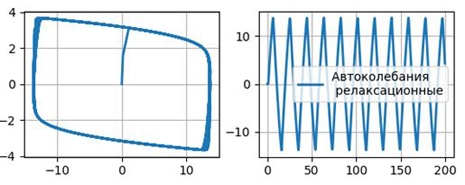
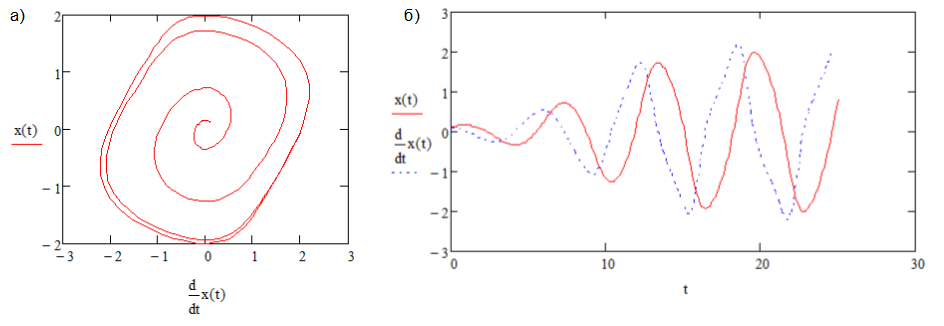
Получим фазовые портреты (слева) и временные реализации колебаний (справа) осциллятора Ван-дер-Поля: λ =0.1, λ =1.1

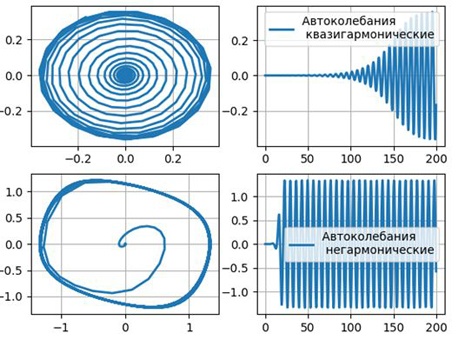
Для λ =10.0

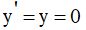
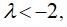
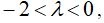
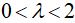
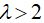
Уравнение Ван-дер-Поля имеет единственную особую точку , которая является устойчивым узлом при устойчивым фокусом при неустойчивым фокусом при и неустойчивым узлом при . Если выполнено условие самовозбуждения, на фазовой плоскости имеется также предельный цикл, отвечающий режиму периодических автоколебаний.

Химические колебания. Брюсселятор

Важным и нетривиальным примером автоколебательных процессов служат некоторые химические реакции. Химические колебания — это колебания концентраций реагирующих веществ.

К настоящему времени известно достаточно много колебательных реакций. Наиболее знаменитая из них была открыта Б.П. Белоусовым в 1950 г. и позднее детально изучена А.М. Жаботинским. Реакция Белоусова — Жаботинского (БЖ) представляет собой процесс окисления малоновой кислоты при взаимодействии в присутствии ионов в качестве катализатора.

В ходе реакции раствор периодически изменяет свой цвет: голубой — красный — голубой — красный и т.д. Кроме простых периодических колебаний, реакция БЖ демонстрирует (в зависимости от условий эксперимента) множество различных типов пространственно-временной динамики, которые окончательно еще не исследованы.

Предложены различные математические модели реакции БЖ (например, модель Филда, Кереса и Нойеса — «орегонатор»), однако ни одна из них не описывает полностью все детали, наблюдаемые в эксперименте.

Мы рассмотрим более простой модельный пример: гипотетическую химическую реакцию, которая получила название Брюсселятор [8]. Уравнения этой реакции имеют вид:

Предполагается, что реагенты A и B имеются в избытке, так что их концентрации можно считать постоянными, а D и E ни в какие реакции не вступают. Составим кинетические уравнения, соответствующие реакции, которые описывают динамику концентраций реагирующих веществ.

Поскольку число актов химической реакции в единицу времени определяется вероятностью столкновения молекул реагентов, скорости изменения концентраций продуктов реакции пропорциональны произведению концентраций соответствующих реагентов с коэффициентами пропорциональности, называемыми константами скоростей реакций. Тогда кинетические уравнения можно записать в виде:

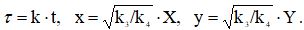
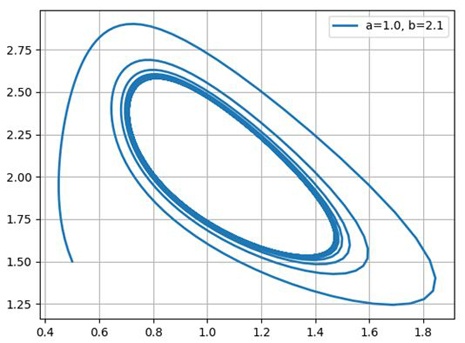
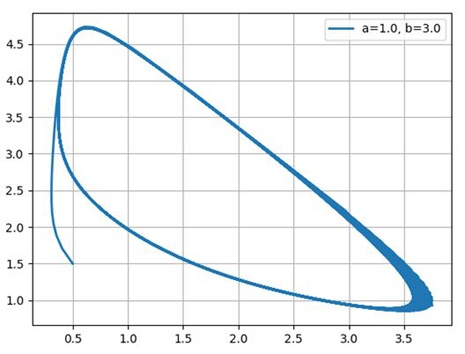
Символами Y,X будем теперь обозначать соответствующие концентрации. Отметим, что из третьего уравнения системы следует, что скорость образования вещества X зависит от его концентрации, т.е. эта стадия реакции носит автокаталитический характер. Приведем уравнения (1) к безразмерному виду, содержащему минимальное число управляющих параметров. Для этого перейдём к новым переменным, Тогда уравнения (1) примут вид:

Построим фазовые портреты для: a=1.0; b=2.1; b=3.0;b=5.0

Таким образом, химический осциллятор демонстрирует поведение, типичное для автоколебательных систем и вполне аналогичное, например, осциллятору Ван-дер-Поля.

Автоколебания в биосистемах (на примере модели Лотки Вольтерра –“Хищник -жертва”)

В динамике популяций есть много примеров, когда изменение численности популяций во времени носит колебательный характер. Одним из самых известных примеров описания динамики взаимодействующих популяций являются уравнения Вольтерра—Лотка.

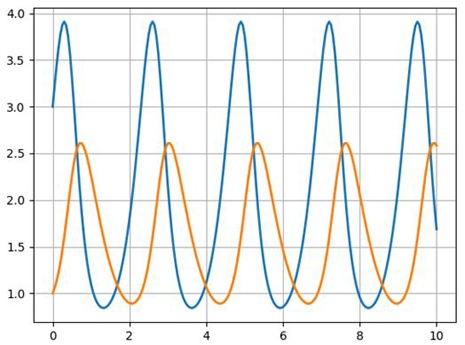
Рассмотрим модель взаимодействия хищников и их добычи, когда между особями одного вида нет соперничества. Пусть x и y— число жертв и хищников соответственно. Предположим, что относительный прирост жертв y’/x равен a-by, a>0, b>0, где a — скорость размножения жертв в отсутствие хищников, -by— потери от хищников.

Развитие популяции хищников зависит от количества пищи (жертв), при отсутствии пищи ( x=0 ) относительная скорость изменения популяции хищников равна y’/y =-c, c>0, наличие пищи компенсирует убывание, и при x>0 имеем y’/y =(-c +d*x), d>0.

Таким образом, система Вольтерра—Лотка имеет вид:

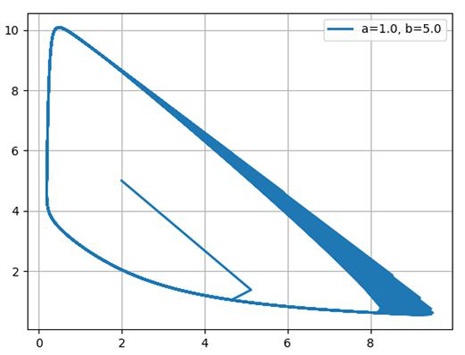
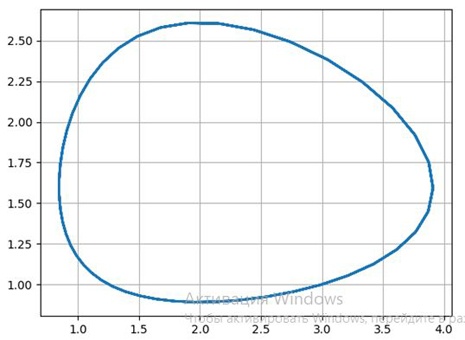
Рассмотрим фазовый портрет системы Вольтерра Лотка, для a=4 b=2.5, c=2, d=1 и графики ее решения с начальным условием x(0)=3, y(0)=1, построенные программой Python для численного решения системы обыкновенных дифференциальных уравнений:

Видно, что процесс имеет колебательный характер. При заданном начальном соотношении числа особей обоих видов 3: 1, обе популяции сначала растут. Когда число хищников достигает величины b=2.5, популяция жертв не успевает восстанавливаться и число жертв начинает убывать.

Уменьшение количества пищи через некоторое время начинает сказываться на популяции хищников и когда число жертв достигает величины x=c/d =2 (в этой точке y’=0), число хищников тоже начинает сокращаться вместе с сокращением числа жертв. Сокращение популяций происходит до тех пор, пока число хищников не достигнет величины y=a/b =1.6 (в этой точке x’=0).

С этого момента начинает расти популяция жертв, через некоторое время пищи становится достаточно, чтобы обеспечить прирост хищников, обе популяции растут, и… процесс повторяется снова и снова.

Рассмотренная модель может описывать поведение конкурирующих фирм, рост народонаселения, численность воюющих армий, изменение экологической обстановки, развитие науки и т.п.

Видео:Python для самых маленьких. Линейные уравнения. Решение задачСкачать

Питон уравнение ван дер поля

Операционная система: Windows.
Лицензия: бесплатно.
Версия: 1.1.0.0.
Аннотация: демонстрируется программа по анализу генератора Ван-дер-Поля, позволяющая наблюдать такие состояния системы, как устойчивый аттрактор, устойчивый и неустойчивый фокус, предельный цикл, образование второго неустойчивого фокуса и предельного цикла.
Скачать: ZIP (архив программы).
Ключевые слова: осциллятор Ван дер Поля, уравнение Ван Дер Поля matlab, дифференциальное уравнение Ван дер Поля, уравнение Ван Дер Поля фазовый портрет, метод Ван Дер Поля пример, уравнение генератор Ван Дер Поля, метод Рунге Кутта 2 порядка, уравнение Ван дер Поля портрет, метод Ван дер Поля, осциллятор Ван дер Поля дуффинга, фазовый портрет уравнения Ван-дер-Поля, решение уравнения Ван-дер-Поля, Бальтазар Ван дер Поль, Ван дер Поль математик, Ван дер Поль маткад, Ван дер Поль уравнение, Ван дер Поль нелинейная теория электрических колебаний, Ван дер Поль программа, Ван Дер Поль генераторы, Ван дер Поль матлаб.

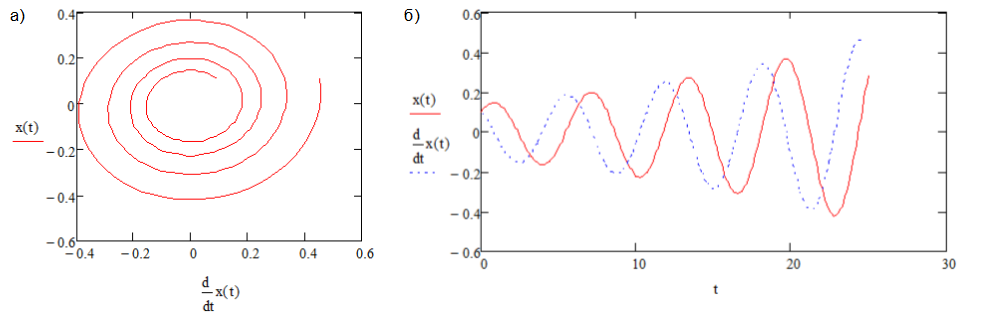
Осциллятор Ван-дер-Поля представляет собой генератор с нелинейным затуханием. Был предложен голландским физиком Бальтазаром Ван-дер-Полем. Ван-дер-Поль выявил колебания, позже названные предельными циклами, а также состояние детерминированного хаоса. Осциллятор Ван-дер-Поля задается дифференциальным уравнением

где x – координата точки, зависящая от времени t, A1 – коэффициент, характеризующий силу затухания колебаний. В результате исследования системы были выявлены нижеуказанные закономерности.

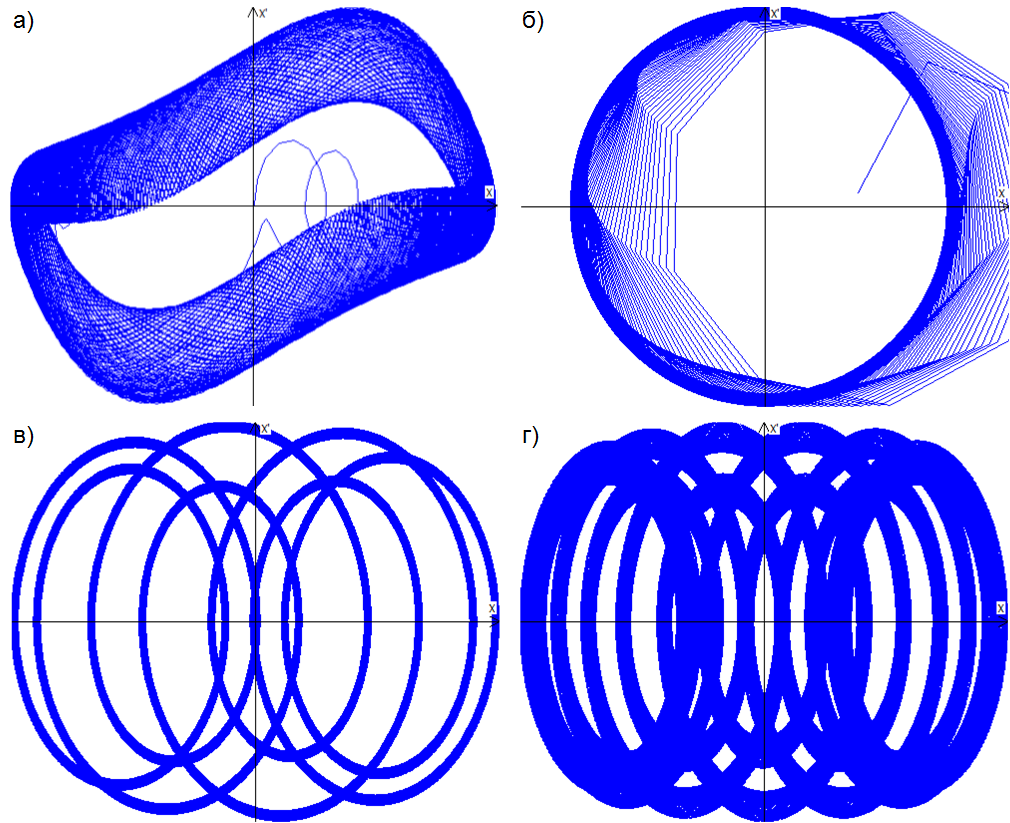
При отрицательных значениях A1

Рис. 1. Устойчивый узел, A1 где x – координата точки, зависящая от времени t, A1 – коэффициент, характеризующий силу затухания колебаний. В результате исследования системы были выявлены нижеуказанные закономерности.

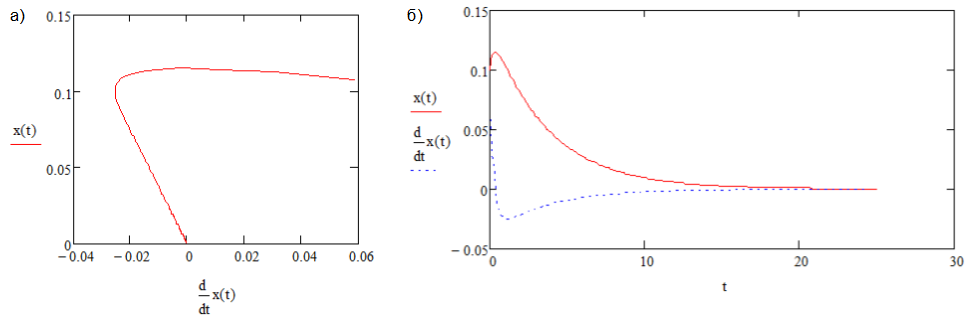
Рис. 2. Устойчивый фокус, A1

Устойчивый предельный цикл (рис.3) образуется при последующем увеличении значения A1, A1

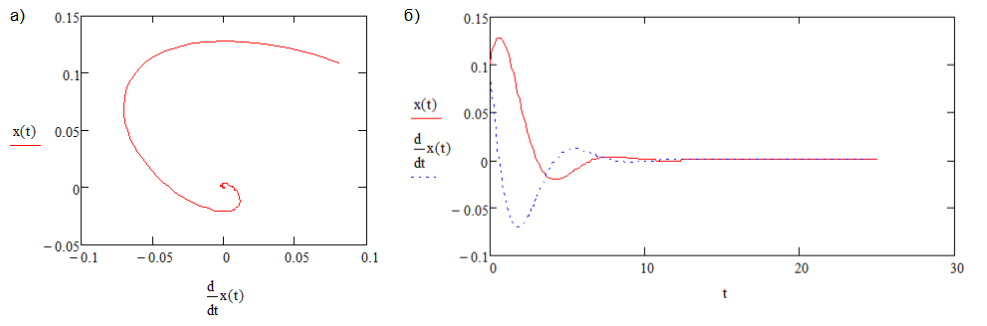
Рис. 3. Устойчивый предельный цикл, A1 Увеличение A1 до положительных значений (A1>0) приводит к потере устойчивости, в результате образуется особая точка вида неустойчивый фокус (рис.4).

Рис. 4. Неустойчивый фокус, A1>0

Дальнейшее увеличение A1 (A1>0) приводит к образованию неустойчивого предельного цикла (рис.5).

Рис. 5. Неустойчивый предельный цикл, A1>0

Модернизированный генератор Ван-дер-Поля позволяет наблюдать автоколебательный режим работы системы. В случае модернизированного осциллятора формула (1) преобразуется к виду (2)

где x – координата точки, а A1, A2, A3 – коэффициенты (A2>0, 0

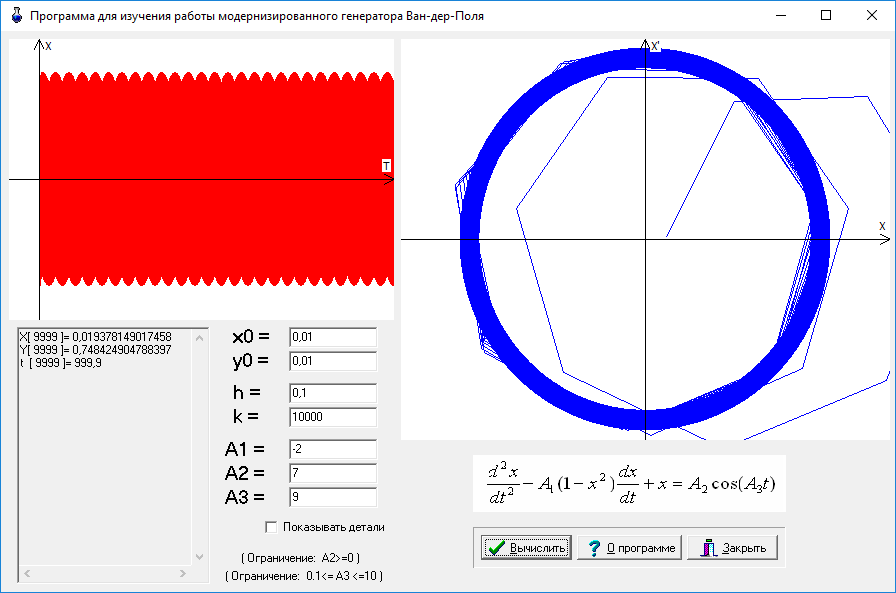
Программа «VanDerPol — программа для изучения работы модернизированного генератора Ван-дер-Поля», реализованная в среде разработки Turbo C++, позволяет смоделировать работу модернизированного генератора Ван-дер-Поля. Построение фазового портрета и графика зависимости решений от времени t ведется на основе метода Рунге-Кутта второго порядка. Интерфейс программы приведен на рис.6.

Рис. 6. Интерфейс программы для изучения работы модернизированного генератора Ван-дер-Поля

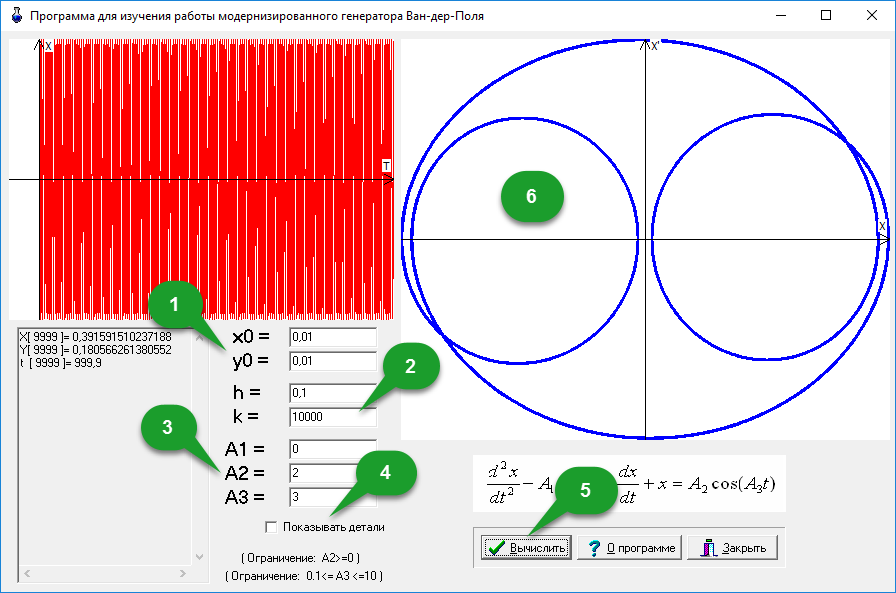
Моделирование работы модернизированного генератора с использованием программы VanDerPol предполагает выполнение следующих шагов (рис.7):

определить начальные координаты (x0,y0);
задать шаг интегрирования h и число итераций k;
установить значение коэффициентов A1, A2, A3;
(опционально) установить индикатор «Показывать детали» для получения деталей решения;
нажать кнопку «Вычислить»;
(опционально) дважды щелкнуть на полученных изображениях для их копирования в буфер обмена.